オンライン用テキストの準備中：6/3(水)までに用意します。 小さい字は補足説明なので、読み飛ばしてもいいです。

このページのオリジナルの作者は 後藤文彦です。

マトリクス構造解析オンライン授業用テキスト
第4回オンライン授業

目次

• 全体系の要素剛性方程式
• 座標変換
• 例題

全体系の要素剛性方程式

前回、局所座標系($y^{\ell}z^{\ell}$系)に横たわる ばね要素に対して、 座標変換できるように$y^{\ell}$方向成分を加えて、 以下のような局所系の要素剛性方程を定義したが、 これを、前回導いた座標変換行列$\mathbf{T}$や$\mathbf{T}^{T}$を 使って、全体座標系の成分で表す方法を考える。
局所系の要素剛性方程式
$ \left( \begin{array}{c} S_{1}^{\ell}\\ N_{1}^{\ell}\\ S_{2}^{\ell}\\ N_{2}^{\ell} \end{array} \right) = \left( \begin{array}{rrrr} 0 & 0 & 0 & 0 \\ 0 & k & 0 & -k \\ 0 & 0 & 0 & 0 \\ 0 & -k & 0 & k \\ \end{array} \right) \left( \begin{array}{c} v_{1}^{\ell}\\ w_{1}^{\ell}\\ v_{2}^{\ell}\\ w_{2}^{\ell} \end{array} \right) $
それぞれの節点の 節点力や節点変位は、 それぞれ$y^{\ell}, z^{\ell}$成分のベクトルだから、 全体系から局所系への座標変換行列$\mathbf{T}$を 使えば、それぞれの節点の成分は以下のように表せる。
$ \left( \begin{array}{c} S_{1}^{\ell}\\ N_{1}^{\ell} \end{array} \right) =\mathbf{T} \left( \begin{array}{c} S_{1}\\ N_{1} \end{array} \right) \\ $
$ \left( \begin{array}{c} S_{2}^{\ell}\\ N_{2}^{\ell} \end{array} \right) =\mathbf{T} \left( \begin{array}{c} S_{2}\\ N_{2} \end{array} \right) \\ $
$ \left( \begin{array}{c} v_{1}^{\ell}\\ w_{1}^{\ell} \end{array} \right) =\mathbf{T} \left( \begin{array}{c} v_{1}\\ w_{1} \end{array} \right) \\ $
$ \left( \begin{array}{c} v_{2}^{\ell}\\ w_{2}^{\ell} \end{array} \right) =\mathbf{T} \left( \begin{array}{c} v_{2}\\ w_{2} \end{array} \right) $
これらを、上の局所系の要素剛性方程式に代入したいのだが、 節点力ベクトル $(S_{1}^{\ell}, N_{1}^{\ell}, S_{2}^{\ell}, N_{2}^{\ell})$ や節点変位ベクトル $(v_{1}^{\ell}, w_{1}^{\ell}, v_{2}^{\ell}, w_{2}^{\ell})$ に1つのマトリクスで一発でかけられるように、 以下のように$4\times 4$のマトリクスで座標変換行列をかけられるようにする。
$ \left( \begin{array}{c} S_{1}^{\ell}\\ N_{1}^{\ell}\\ S_{2}^{\ell}\\ N_{2}^{\ell} \end{array} \right) = \left( \begin{array}{cc} \mathbf{T} & \mathbf{O}\\ \mathbf{O} & \mathbf{T}\\ \end{array} \right) \left( \begin{array}{c} S_{1}\\ N_{1}\\ S_{2}\\ N_{2} \end{array} \right) = \left( \begin{array}{rrrr} \cos\theta & \sin\theta & 0 & 0 \\ -\sin\theta & \cos\theta & 0 & 0 \\ 0 & 0 & \cos\theta & \sin\theta \\ 0 & 0 & -\sin\theta & \cos\theta \end{array} \right) \left( \begin{array}{c} S_{1}\\ N_{1}\\ S_{2}\\ N_{2} \end{array} \right) \\ $
$ \left( \begin{array}{c} v_{1}^{\ell}\\ w_{1}^{\ell}\\ v_{2}^{\ell}\\ w_{2}^{\ell} \end{array} \right) = \left( \begin{array}{cc} \mathbf{T} & \mathbf{O}\\ \mathbf{O} & \mathbf{T}\\ \end{array} \right) \left( \begin{array}{c} v_{1}\\ w_{1}\\ v_{2}\\ w_{2} \end{array} \right) $
そして、これらを上の要素剛性方程式に代入すれば、 以下のようになる。
$ \left( \begin{array}{cc} \mathbf{T} & \mathbf{O}\\ \mathbf{O} & \mathbf{T}\\ \end{array} \right) \left( \begin{array}{c} S_{1}\\ N_{1}\\ S_{2}\\ N_{2} \end{array} \right) = \left( \begin{array}{rrrr} 0 & 0 & 0 & 0 \\ 0 & k & 0 & -k \\ 0 & 0 & 0 & 0 \\ 0 & -k & 0 & k \\ \end{array} \right) \left( \begin{array}{cc} \mathbf{T} & \mathbf{O}\\ \mathbf{O} & \mathbf{T}\\ \end{array} \right) \left( \begin{array}{c} v_{1}\\ w_{1}\\ v_{2}\\ w_{2} \end{array} \right) $
これで、節点力も節点変位も、すべて全体系($yz$系)の成分だけで 表すことができた。 でも、左辺の座標変換のマトリクスがちょっと邪魔だ。 これを消すにはどうすればいいだろうか。 $\mathbf{T}$に$\mathbf{T}^{T}$をかければ単位行列になるのだから、 両辺に左から、
$ \left( \begin{array}{ll} \mathbf{T}^{T} & \mathbf{O}\\ \mathbf{O} & \mathbf{T}^{T} \end{array} \right) $
をかければいいのではないか。そうすると、左辺の座標変換のマトリクスが 消えて、以下のような式となる。
全体系の要素剛性方程式
$ \left( \begin{array}{c} S_{1}\\ N_{1}\\ S_{2}\\ N_{2} \end{array} \right) = \left( \begin{array}{ll} \mathbf{T}^{T} & \mathbf{O}\\ \mathbf{O} & \mathbf{T}^{T}\\ \end{array} \right) \left( \begin{array}{rrrr} 0 & 0 & 0 & 0 \\ 0 & k & 0 & -k \\ 0 & 0 & 0 & 0 \\ 0 & -k & 0 & k \\ \end{array} \right) \left( \begin{array}{cc} \mathbf{T} & \mathbf{O}\\ \mathbf{O} & \mathbf{T}\\ \end{array} \right) \left( \begin{array}{c} v_{1}\\ w_{1}\\ v_{2}\\ w_{2} \end{array} \right) $
これが全体系での要素剛性方程式である。 両端が節点2, 3の要素や節点3, 4の要素とかにも、 同様に全体系の節点力と節点変位で表したこの形式の 要素剛性方程式が書けるから、 色んな方向を向いた局所系の要素剛性方程式を、 全体系で重ね合わせることができる。

例題

全体系から右ねじ回りに$\theta=30^{\circ}$傾いた$z^{\ell}$に 横たわる ばね要素の節点1が固定されていて、 節点2を軸に沿って外力$P$で引っ張る （ということは、節点2が$z^{\ell}$方向にしか動かないように拘束されている ということになるのだが）問題を、 全体系($yz$系)で解いてみよう。 もちろん、これは、局所系($y^{\ell}z^{\ell}$系)で解けば、 第1回のばねの問題と同じなので、簡単に解ける。 フックの法則で、ばねの伸びは軸に沿って$\frac{P}{k}$だし、 軸力はどこで切っても$P$だ。 しかし、それを全体系で表すと、$y$方向、$z$方向の成分が それぞれ発生する。それを全体系の要素剛性方程式を作って、 解いてみようということ。
まず、局所系($y^{\ell}z^{\ell}$系)の要素剛性方程式は、
$ \left( \begin{array}{c} S_{1}^{\ell}\\ N_{1}^{\ell}\\ S_{2}^{\ell}\\ N_{2}^{\ell} \end{array} \right) = \left( \begin{array}{rrrr} 0 & 0 & 0 & 0 \\ 0 & k & 0 & -k \\ 0 & 0 & 0 & 0 \\ 0 & -k & 0 & k \\ \end{array} \right) \left( \begin{array}{c} v_{1}^{\ell}\\ w_{1}^{\ell}\\ v_{2}^{\ell}\\ w_{2}^{\ell} \end{array} \right) $
となる。全体系の要素剛性方程式は、
$ \left( \begin{array}{c} S_{1}\\ N_{1}\\ S_{2}\\ N_{2} \end{array} \right) = \left( \begin{array}{ll} \mathbf{T}^{T} & \mathbf{O}\\ \mathbf{O} & \mathbf{T}^{T}\\ \end{array} \right) \left( \begin{array}{rrrr} 0 & 0 & 0 & 0 \\ 0 & k & 0 & -k \\ 0 & 0 & 0 & 0 \\ 0 & -k & 0 & k \end{array} \right) \left( \begin{array}{cc} \mathbf{T} & \mathbf{O}\\ \mathbf{O} & \mathbf{T}\\ \end{array} \right) \left( \begin{array}{c} v_{1}\\ w_{1}\\ v_{2}\\ w_{2} \end{array} \right) $
となる。$\theta=30^{\circ}$だから、$\mathbf{T}$は、
$ \mathbf{T}= \left( \begin{array}{cc} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{array} \right) = \left( \begin{array}{cc} \cos 30^{\circ} & \sin 30^{\circ} \\ -\sin 30^{\circ} & \cos 30^{\circ} \end{array} \right) = \left( \begin{array}{cc} \frac{\sqrt{3}}{2} & \frac{1}{2} \\ -\frac{1}{2} & \frac{\sqrt{3}}{2} \end{array} \right) $
$ \mathbf{T}^{T}= \left( \begin{array}{cc} \frac{\sqrt{3}}{2} & -\frac{1}{2} \\ \frac{1}{2} & \frac{\sqrt{3}}{2} \end{array} \right) $

この座標変換行列を全体系の要素剛性方程式に代入して、 右の板書みたいに マトリクス3つのかけ算をやると、以下のような 全体系の要素剛性方程式が求まる。
$ \left( \begin{array}{c} S_{1}\\ N_{1}\\ S_{2}\\ N_{2} \end{array} \right) = \left( \begin{array}{rrrr} 1 & -\sqrt{3} & -1 & \sqrt{3} \\ -\sqrt{3} & 3 & \sqrt{3} & -3 \\ -1 & \sqrt{3} & 1 & -\sqrt{3} \\ \sqrt{3} & -3 & -\sqrt{3} & 3 \end{array} \right) \left( \begin{array}{c} v_{1}\\ w_{1}\\ v_{2}\\ w_{2} \end{array} \right) $
では、この全体系の要素剛性方程式を用いて、 (1)節点変位を求め、 (2) 節点1, 2の近傍でばねを切断したときの断面力を、 求めた節点変位を用いて節点力$(S_{1}, N_{1}, S_{2}, N_{2})$として求め、 (3)（切断した）ばね要素の各節点に作用する力を、正の値で描ける向きに矢印を向けて図示せよ。

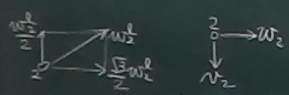この式を解くためには全体系で境界条件を与えなければいけないが、 実はそれが難しい。 まず局所系での境界条件は、 節点1の$v_{1}^{\ell}=w_{1}^{\ell}=0$の他に、 節点2の$v_{2}^{\ell}=0$もあるのだが、 この境界条件を全体系で与えることができない。 ひとまず、$v_{1}=w_{1}=0$の境界条件だけを与えて解くと、 同じ式が2つ出てくるだけなので、$v_{2}, w_{2}$は求まらない。 そこで、$v_{2}^{\ell}=0$が使えない代わりに、 もう一つ条件を使っていいことにする。 この ばね要素は、$z^{\ell}$方向にしか伸びず、 つまり局所系では、$w_{2}^{\ell}$しか発生せず、 $v_{2}^{\ell}=0$である。 というか、上の全体系の要素剛性方程式は、 要素の向きが$\theta=30^{\circ}$を保つという仮定の元で成り立っている。 そうすると、変位成分は$w_{2}^{\ell}$しかないので、 これを$yz$方向に分解すると、 $v_{2}=-\frac{w_{2}^{\ell}}{2}, w_{2}=\frac{\sqrt{3}}{2}w_{2}^{\ell}$ ということになり、これらから $w_{2}=-\sqrt{3}v_{2}$という関係が求まる。 この関係も使っていいことにする。

こたえは、ここ、 解説の動画は 第4回 例題その1, 第4回 例題その2。

2022年度 小テスト： 問題, 解答
2021年度 小テスト： 問題, 解答
2020年度 小テスト： 問1, 問2, 問3, 問4, 解答