マトリクス構造解析オンライン授業用テキスト
第6回オンライン授業
オンライン用テキストの準備中：6/17(水)までに用意します。 小さい字は補足説明なので、読み飛ばしてもいいです。
前回まで、ばね要素（トラス要素）の剛性方程式をやったが、 ばね要素では、曲げやせん断の作用する梁や剛結骨組（ラーメン）は解けない。 ということで、 今回から、梁の剛性方程式の使い方を説明する。 梁の剛性方程式をどうやって導くのかという話は、この授業ではやらない。 ただ、構造力学IIの知識の範囲で導くことができないわけでもないので、 興味のある人は、 構造力学IIの範囲で梁の剛性マトリクスを導く を参照してほしい。
ということで、まずは、梁要素の節点力と節点変位を定義する。
簡単のため、まずは軸力の作用しない問題を考える。
鉛直荷重やモーメントしか作用しない構造力学の梁の問題を解くには、
ひとまず、これで十分だ。
座標は、2次元に拡張した ばね要素と同様に、
要素軸に沿って右向きに$z$, 下向きに$y$とする。
節点力は座標方向が正なので、既に2次元に拡張した ばね要素で定義したように、
鉛直下向き($y$方向に)鉛直方向の節点力$S_{1}, S_{2}$と
鉛直方向の節点変位$v_{1}, v_{2}$を定義する。
軸力の作用しない梁の問題が解けるように、
$x$軸右ねじまわりを正として、
節点モーメント
$M_{1}, M_{2}$と
節点の回転角$\theta_{1}, \theta_{2}$を図のように定義する。
モーメントの正の向きは、構造力学の下側引張が正ではなく、
$x$軸右ねじまわりが正なので、注意する。
この梁の剛性方程式は以下のように与えられる。
$EI$は曲げ剛性である。
導出が気になる人は、
ここ参照。
なお、
ここでは
$y$が下向き、$z$が右向きの
$yz$座標系の、
$z$軸に横たわる梁要素に対して、右ねじ系で剛性方程式を導いているから、
$x$軸右ねじ回りのモーメントや回転角は、$yz$平面上では反時計回りに
定義される。
一方、
$y$が下向き、$x$が右向きの
$x$軸に梁要素が横たわる$xy$座標系を用いているテキストでは、
$z$軸右ねじ回りのモーメントや回転角は、$xy$平面上では時計回りに
定義されるので、以下に示すマトリクスとは成分の符号が逆になっていたりする
ので、他のテキストや論文等のマトリクスを参照する際は、
常に、どういう座標で定義されているのかについて、
注意が必要である。
$
\left(
\begin{array}{c}
S_{1}\\
M_{1}\\
S_{2}\\
M_{2}
\end{array}
\right)
=
\left(
\begin{array}{cccc}
\frac{12EI}{\ell^{3}} &
-\frac{6EI}{\ell^{2}} &
-\frac{12EI}{\ell^{3}}&
-\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} \\
-\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} &
\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}\\
\theta_{1}\\
v_{2}\\
\theta_{2}
\end{array}
\right)
$
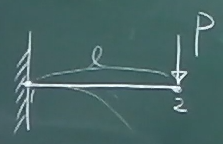この剛性方程式を使って、図のような片持ち梁を解いてみる。
左端が節点1で固定端。右端が節点2で、$y$方向に荷重$P$を受ける。
外力条件は、$S_{2}=P$, それ以外の節点力はゼロ。
境界条件は、$v_{1}=\theta_{1}=0$
ばね要素のときと同様にこれらの条件を上記の剛性方程式に適用すると、
以下のようになる。
$
\left(
\begin{array}{c}
0\\
0\\
P\\
0
\end{array}
\right)
=
\left(
\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 &
\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} \\
0 & 0 &
\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}\\
\theta_{1}\\
v_{2}\\
\theta_{2}
\end{array}
\right)
$
3行目と4行目を解けばいいから、両辺を$EI$で割ってから展開し
$\frac{P}{EI}=\frac{12}{\ell^{3}}v_{2}+\frac{6}{\ell^{2}}\theta_{2}$
$0=\frac{6}{\ell^{2}}v_{2}+\frac{4}{\ell}\theta_{2}$
これを解くと、
$v_{2}=\frac{P\ell^{3}}{3EI}$,
$\theta_{2}=-\frac{P\ell^{2}}{2EI}$と求まる。
構造力学IIで、$M=-EIv''$を積分して求めた答えによると、
$v(z)=\frac{P}{6EI}(3\ell z^{2}-z^{3})$だから、
$z=\ell$を代入すれば、先端のたわみは、
$v(\ell)=\frac{P\ell^{3}}{3EI}$で$v_{2}$と一致する。
先端のたわみ角は、
$v'(z)=\frac{P}{6EI}(6\ell z-3z^{2})$
に$z=\ell$を代入すれば、
$v'(\ell)=\frac{P\ell^{2}}{2EI}$となる。
たわみ角$v'(\ell)$は、$z$が増加したときに$v(z)$が$y$方向に増加する傾きだから、
時計回り($x$軸左ねじまわり)の回転となる。
$\theta_{2}$は$x$軸右ねじまわりの回転角だから、
$\theta_{2}=-v'(\ell)$で合っている。
ばね要素のときと同じ手順で、
求めた節点変位を、もとの要素剛性方程式に代入して、
反力（や断面力）を求める。
断面力というのは、節点の近傍で要素を切断したときに、
その切断面に作用している内力としての節点力だから、
（外力条件や境界条件を入れる前の）もとの要素剛性方程式に
節点変位を代入して求める。
この1要素の問題の場合、固定端側の切断面に作用する内力は
反力と一致するし、自由端側の切断面に作用する内力は外力に一致する。
$
\left(
\begin{array}{c}
S_{1}\\
M_{1}\\
S_{2}\\
M_{2}
\end{array}
\right)
=
\left(
\begin{array}{cccc}
\frac{12EI}{\ell^{3}} &
-\frac{6EI}{\ell^{2}} &
-\frac{12EI}{\ell^{3}}&
-\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} \\
-\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} &
\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{c}
0 \\
0 \\
\frac{P\ell^{3}}{3EI} \\
-\frac{P\ell^{2}}{2EI}
\end{array}
\right)
=
\left(
\begin{array}{c}
-4P+3P \\
2P\ell-P\ell \\
4P-3P \\
2P\ell-2P\ell
\end{array}
\right)
=
\left(
\begin{array}{c}
-P \\
P\ell \\
P \\
0
\end{array}
\right)
$
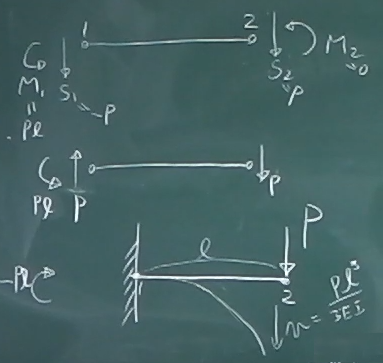求まった節点力を、まずは、求まった通りの
$S_{1}, M_{1}, S_{2}, M_{2}$のまま描いてみる。
次に、符号がマイナスのものは実際の向きにして、
値がゼロのものは消す。
すると、節点1には片持ち梁の鉛直反力とモーメント反力が、
節点2には外力$P$が作用してつりあっているのがわかる。
ちなみに、構造力学IIでは、
反力モーメントも曲げモーメントと同じように下側引張を正の
向きで書くことにしているが、
そうすると、反時計回りに$P\ell$の反力モーメントは、
下側引張が正（左端の場合は時計回り）で書くと$-P\ell$となり、
「負曲げ」ということになる。
つまり、梁の上側が引張になっているということである。
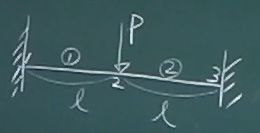途中に外力を受ける問題の場合、外力を受ける部分に節点を設けなくては
いけないから、複数の要素で解く必要がある。
図のような両端固定の梁で、中央に外力を受ける問題を2要素の梁要素で解いてみる。
不静定梁で、力のつりあいから曲げモーメントは求まらないから、
$EIv''''=0$を積分して解くと
それなりに大変である。
ばね要素のときと同様に、
要素をばらばらにして、
それぞれの要素ごとの要素剛性方程式を書く。
節点2の節点力$S_{2}$と$M_{2}$は、ばね要素のときと同様に、
要素①と要素②に
$S_{2}=S_{2}^{①}+S_{2}^{②}$,
$M_{2}=M_{2}^{①}+M_{2}^{②}$と分配される。
要素①の要素剛性方程式
$
\left(
\begin{array}{c}
S_{1}\\
M_{1}\\
S_{2}^{①}\\
M_{2}^{①}
\end{array}
\right)
=
\left(
\begin{array}{cccc}
\frac{12EI}{\ell^{3}} &
-\frac{6EI}{\ell^{2}} &
-\frac{12EI}{\ell^{3}}&
-\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} \\
-\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} &
\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}\\
\theta_{1}\\
v_{2}\\
\theta_{2}
\end{array}
\right)
\\
$
要素②の要素剛性方程式
$
\left(
\begin{array}{c}
S_{2}^{②}\\
M_{2}^{②}\\
S_{3}\\
M_{3}
\end{array}
\right)
=
\left(
\begin{array}{cccc}
\frac{12EI}{\ell^{3}} &
-\frac{6EI}{\ell^{2}} &
-\frac{12EI}{\ell^{3}}&
-\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} \\
-\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} &
\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{c}
v_{2}\\
\theta_{2}\\
v_{3}\\
\theta_{3}
\end{array}
\right)
$
ばね要素のときと同じ要領で、全体剛性方程式を組み立てると
以下のようになる。
$
\left(
\begin{array}{c}
S_{1}\\
M_{1}\\
S_{2}\\
M_{2}\\
S_{3}\\
M_{3}
\end{array}
\right)
=
\left(
\begin{array}{cccccc}
\frac{12EI}{\ell^{3}} &
-\frac{6EI}{\ell^{2}} &
-\frac{12EI}{\ell^{3}}&
-\frac{6EI}{\ell^{2}} & 0 & 0 \\
-\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} & 0 & 0 \\
-\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} &
\frac{12EI}{\ell^{3}} + \frac{12EI}{\ell^{3}}&
\frac{6EI}{\ell^{2}} -\frac{6EI}{\ell^{2}} &
-\frac{12EI}{\ell^{3}}&
-\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} &
\frac{6EI}{\ell^{2}} -\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell}+\frac{4EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} \\
0 & 0 & -\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} &
\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} \\
0 & 0 & -\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}\\
\theta_{1}\\
v_{2}\\
\theta_{2}\\
v_{3}\\
\theta_{3}
\end{array}
\right)
\\
$
つまり
$
\left(
\begin{array}{c}
S_{1}\\
M_{1}\\
S_{2}\\
M_{2}\\
S_{3}\\
M_{3}
\end{array}
\right)
=
\left(
\begin{array}{cccccc}
\frac{12EI}{\ell^{3}} &
-\frac{6EI}{\ell^{2}} &
-\frac{12EI}{\ell^{3}}&
-\frac{6EI}{\ell^{2}} & 0 & 0 \\
-\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} & 0 & 0 \\
-\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} &
\frac{24EI}{\ell^{3}}&
0 &
-\frac{12EI}{\ell^{3}}&
-\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} &
0 &
\frac{8EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} \\
0 & 0 & -\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} &
\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} \\
0 & 0 & -\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}\\
\theta_{1}\\
v_{2}\\
\theta_{2}\\
v_{3}\\
\theta_{3}
\end{array}
\right)
\\
$
外力条件は、$S_{2}=P$, その他の節点力はゼロ。
境界条件は、節点1と節点2が固定だから、
$v_{1}=\theta_{1}=v_{2}=\theta_{2}=0$.
これらを上の式に適用すると、以下のようになる。
$
\left(
\begin{array}{c}
0 \\
0 \\
P \\
0 \\
0 \\
0
\end{array}
\right)
=
\left(
\begin{array}{cccccc}
1 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & \frac{24EI}{\ell^{3}} & 0 & 0 & 0 \\
0 & 0 & 0 & \frac{8EI}{\ell} & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 \\
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}\\
\theta_{1}\\
v_{2}\\
\theta_{2}\\
v_{3}\\
\theta_{3}
\end{array}
\right)
\\
$
拍子抜けするほど簡単な式になってしまった。
これを解くと、$v_{2}=\frac{P\ell^{3}}{24EI}$, $\theta_{2}=0$と求まる。
マトリクスを書くのは大変だが
（実際に手計算する際は、いちいち全てを書く必要もないが）、
$EIv''''=0$を積分して解くより、
だいぶ楽に求まるのではないだろうか。
では、求まった節点変位を元の要素剛性方程式に代入して、
要素をばらばらの状態にしたときの内力としての節点力を求める。
要素①の要素剛性方程式
$
\left(
\begin{array}{c}
S_{1}\\
M_{1}\\
S_{2}^{①}\\
M_{2}^{①}
\end{array}
\right)
=
\left(
\begin{array}{cccc}
\frac{12EI}{\ell^{3}} &
-\frac{6EI}{\ell^{2}} &
-\frac{12EI}{\ell^{3}}&
-\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} \\
-\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} &
\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{c}
0\\
0\\
\frac{P\ell^{3}}{24EI}\\
0
\end{array}
\right)
=
\left(
\begin{array}{c}
-\frac{P}{2}\\
\frac{P\ell}{4}\\
\frac{P}{2}\\
\frac{P\ell}{4}
\end{array}
\right)
$
要素②の要素剛性方程式
$
\left(
\begin{array}{c}
S_{2}^{②}\\
M_{2}^{②}\\
S_{3}\\
M_{3}
\end{array}
\right)
=
\left(
\begin{array}{cccc}
\frac{12EI}{\ell^{3}} &
-\frac{6EI}{\ell^{2}} &
-\frac{12EI}{\ell^{3}}&
-\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} \\
-\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} &
\frac{12EI}{\ell^{3}} &
\frac{6EI}{\ell^{2}} \\
-\frac{6EI}{\ell^{2}} &
\frac{2EI}{\ell} &
\frac{6EI}{\ell^{2}} &
\frac{4EI}{\ell}
\end{array}
\right)
\left(
\begin{array}{c}
\frac{P\ell^{3}}{24EI}\\
0\\
0\\
0
\end{array}
\right)
=
\left(
\begin{array}{c}
\frac{P}{2}\\
-\frac{P\ell}{4}\\
-\frac{P}{2}\\
-\frac{P\ell}{4}
\end{array}
\right)
$
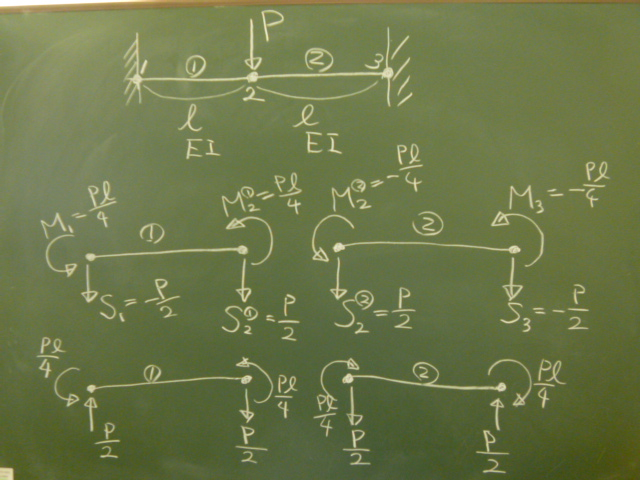求まった節点力をまず、求まった通りの
$S_{2}^{①}$とか$M_{2}^{①}$のまま描いてみる。
次に、負の値を持つものは、実際の向きに描き直してやる。
そうすると、
要素①では、
互いに逆向きの鉛直力が時計回りに$\frac{P\ell}{2}$のモーメントをつくり、
両端に反時計回りに$\frac{P\ell}{4}$のモーメントが2つぶんとつりあっているし、
要素②では、
互いに逆向きの鉛直力が反時計回りに$\frac{P\ell}{2}$のモーメントをつくり、
両端に時計回りに$\frac{P\ell}{4}$のモーメントが2つぶんとつりあっている
のがわかる。
節点2で要素①と要素②をくっつけると、
互いに逆向きのモーメントは作用・反作用でプラマイゼロになる一方、
鉛直力は$\frac{P}{2}+\frac{P}{2}=P$が残る。
節点2は、
くっついた状態で外力$P$が作用しているから、これでいいのだ。
小テストは、上記の2要素の問題程度の簡単な問題を出します。 マトリクスで手計算で解く場合、実は不静定次数が高く、拘束の多い問題の 方が、境界条件でほとんど0になってくれるので解きやすくなります。 未知数が2つぐらいの連立で解ける程度の問題ということで。
2022年度小テスト：
問,
解答
2021年度小テスト：
問,
解答
2020年度小テスト：
問1,
問2,
問3,
解答
