オンライン用テキストの準備中：5/20(水)までに用意します。 小さい字は補足説明なので、読み飛ばしてもいいです。

このページのオリジナルの作者は 後藤文彦です。

マトリクス構造解析オンライン授業用テキスト
第2回オンライン授業

目次

• ばねの剛性方程式（2要素）
• 例題（2要素）
• 例題（2要素）

ばねの剛性方程式（2要素）

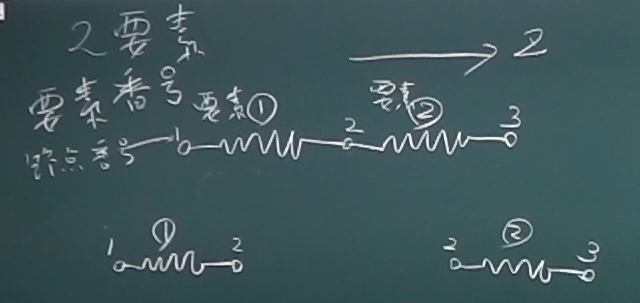トラスみたいに部材がいっぱいあるものを ばね要素（トラス要素）で解く場合には、複数の要素を つなげて解かないといけない。 まずは、$z$軸上で2つの要素が図のようにつながっている問題を考えてみる。 要素が複数ある場合は、要素を区別する必要があるので、 $z$軸上に並ぶ要素の左側から順に、 要素①、要素②と、○付き数字で要素番号を与えることにする。 節点番号については、$z$軸上で左から順に、1, 2, 3と与える。

前回 導いたばねの剛性方程式は1要素の剛性方程式だけど、 これを2要素に適用するには、 ばね要素を1要素ずつに切って考えてやればよい。 節点2のところで ばね要素を切り離すと、 節点2は、もともとくっついている節点だから、 切り離しても、要素①の右端の節点は節点2, 要素②の左端の節点は節点2となる。

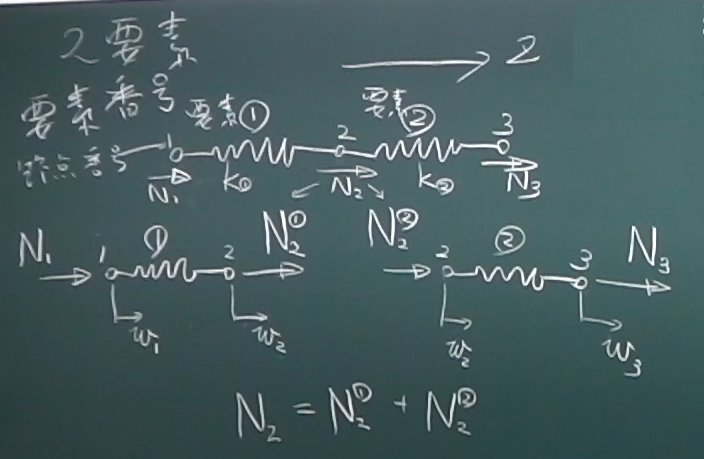次に、各要素の節点変位と節点力を考える。 節点変位については、各節点ごとに$z$軸の正方向が正の節点変位を $w_{1}, w_{2}, w_{3}$と与える。 節点2は、もともとくっついているわけだから、 要素①と要素②に切り離しても、 要素①の右端の$w_{2}$も要素②の左端の$w_{2}$も同じ変位として扱ってよい。 もし、これらが同じでなかったら、 節点2で、要素①と②がちぎれたり、 互いにめり込んだりしていることになってしまうが、 そういう状態は想定していない。 節点力も、 各節点に$z$軸の正方向が正の節点力を $N_{1}, N_{2}, N_{3}$と与える。 さて、これを要素①と要素②に切り離した場合、 節点2の節点力$N_{2}$は、 要素①の節点2と要素②の節点2に、分配されることになる （どういう比率で、あるいはどういう符号で分配されるのかは、 今は、よくわからなくてもよい）。 構造力学的に考えれば、切り離した切断面には、 内力としての軸力が発生しなければならないから、 それらの軸力をそれぞれ$z$軸の正方向を正とする向きに節点力として 与えると考えてもよい。 それで節点力の名前の付け方だが、 要素①の節点2の節点力は、 $N_{2}$のうち、要素①に分配されるぶんという意味で、 $N_{2}^{①}$と書くことにし、 要素②の節点2の節点力は、 $N_{2}$のうち、要素②に分配されるぶんという意味で、 $N_{2}^{②}$と書くことにする。 そうすると、これらの節点力はくっつけると、$N_{2}$にならなければならないので、
$N_{2}=N_{2}^{①}+N_{2}^{②}$
の関係が成り立たなければならない。 もし、節点2に外力が作用してなければ、$N_{2}=0$だから、 $N_{2}^{②}=-N_{2}^{①}$となり、これは作用・反作用の関係で くっつけるとゼロということになる。

要素①と要素②のばね定数をそれぞれ$k_{①},\; k_{②}$と書くことにして、 要素①と要素②について、 1要素の剛性方程式を書いてみると次のようになる。
要素①：
$ \left( \begin{array}{c} N_{1}\\ N_{2}^{①} \end{array} \right) = \left( \begin{array}{cc} k_{①} & -k_{①} \\ -k_{①} & k_{①} \end{array} \right) \left( \begin{array}{c} w_{1}\\ w_{2} \end{array} \right) $

要素②：
$ \left( \begin{array}{c} N_{2}^{②} \\ N_{3} \end{array} \right) = \left( \begin{array}{cc} k_{②} & -k_{②} \\ -k_{②} & k_{②} \end{array} \right) \left( \begin{array}{c} w_{2}\\ w_{3} \end{array} \right) $
このように、1要素ずつに切り離した要素について書いた剛性方程式を 要素剛性方程式と言う。 また、 それぞれの要素剛性方程式の剛性マトリクスを要素剛性マトリクスとか 要素剛性行列と言う。

全体剛性方程式

たくさんの要素がある問題をコンピューターで解く場合は、 それぞれの要素の剛性マトリクスを重ね合わせて 1つの大きなマトリクスを作ってから解いた方が効率がよい。 では、要素①と要素②の要素剛性方程式を重ね合わせてみよう。 まずは、要素剛性マトリクスを節点変位ベクトルにかけて、 1行ずつの式に書いてみる。
$N_{1}=k_{①}w_{1}-k_{①}w_{2}$
$N_{2}^{①}=-k_{①}w_{1}+k_{①}w_{2}$
$N_{2}^{②}=k_{②}w_{2}-k_{②}w_{3}$
$N_{3}=-k_{②}w_{2}+k_{②}w_{3}$
となるだろう。 ここで、さきほどの $N_{2}=N_{2}^{①}+N_{2}^{②}$に$N_{2}^{①}$と$N_{2}^{②}$を代入すれば、
$N_{2}=N_{2}^{①}+N_{2}^{②}$
$=-k_{①}w_{1}+k_{①}w_{2}+k_{②}w_{2}-k_{②}w_{3}$
$=-k_{①}w_{1}+(k_{①}+k_{②})w_{2}-k_{②}w_{3}$
となる。 ここで、節点力ベクトル$(N_{1}, N_{2}, N_{3})$と 節点変位ベクトル$(w_{1}, w_{2}, w_{3})$を使って、以下の3本の式
$N_{1}=k_{①}w_{1}-k_{①}w_{2}$
$N_{2}=-k_{①}w_{1}+(k_{①}+k_{②})w_{2}-k_{②}w_{3}$
$N_{3}=-k_{②}w_{2}+k_{②}w_{3}$
を剛性方程式の形にまとめてやれば、以下のようになる。
$ \left( \begin{array}{c} N_{1}\\ N_{2}\\ N_{3} \end{array} \right) = \left( \begin{array}{ccc} k_{①} & -k_{①} & 0 \\ -k_{①} & k_{①}+k_{②} & -k_{②} \\ 0 & -k_{②} & k_{②} \end{array} \right) \left( \begin{array}{c} w_{1}\\ w_{2}\\ w_{3} \end{array} \right) $
このように、複数の要素剛性方程式を1つに重ね合わせた剛性方程式を 全体剛性方程式と言う。 また、全体剛性方程式の剛性マトリクスを 全体剛性マトリクスとか全体剛性行列と言う。

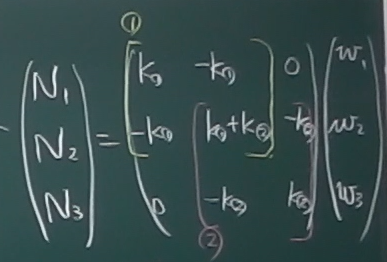この2要素の全体剛性マトリクスをよく見てみると、 左上に要素①の剛性マトリクスがあり、 右下に要素②の剛性マトリクスがあり、真ん中でそれらの重なった部分の 成分が足し合わされている。

一般に、一方向に要素が要素①、要素②、要素③、、、と並んでいる場合、 全体剛性マトリクスは、 左上から右下に向かって、要素①の要素剛性マトリクス、 要素②の要素剛性マトリクス、要素③の要素剛性マトリクス、、、と並んで行き、 それらの重なりあったところの成分どうしが足し合わされる （その他の部分の成分は0）みたいな形になる。

例題(2要素)

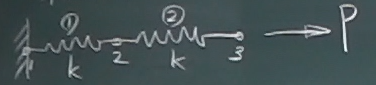例題を解いてみる。 図のような ばね構造系について、 (1)剛性方程式を用いて節点変位を求め、 (2)求めた節点変位を用いて反力・断面力を求め、 (3)ばね要素の各節点に作用する力を、正の値で描ける向きに矢印を向けて図示せよ。
今回は、節点2を切り離すと内力としての断面力（軸力）も発生する。

手順1: 要素剛性方程式をたてる

ばね定数$k_{①}=k_{②}=k$を上の2要素の要素剛性方程式に代入すれば、 以下のようになる。
要素①：
$ \left( \begin{array}{c} N_{1}\\ N_{2}^{①} \end{array} \right) = \left( \begin{array}{cc} k & -k\\ -k & k \end{array} \right) \left( \begin{array}{c} w_{1}\\ w_{2} \end{array} \right) $

要素②：
$ \left( \begin{array}{c} N_{2}^{②} \\ N_{3} \end{array} \right) = \left( \begin{array}{cc} k & -k \\ -k & k \end{array} \right) \left( \begin{array}{c} w_{2}\\ w_{3} \end{array} \right) $

手順2: 全体剛性方程式を組み立てる

ばね定数は要素①も要素②も$k$で、 それぞれの要素剛性マトリクスが重なる$k_{22}$成分は$k+k$となるから、 全体剛性方程式は、 以下のようになる。 $ \left( \begin{array}{c} N_{1}\\ N_{2}\\ N_{3} \end{array} \right) = \left( \begin{array}{ccc} k & -k & 0 \\ -k & 2k & -k \\ 0 & -k & k \end{array} \right) \left( \begin{array}{c} w_{1}\\ w_{2}\\ w_{3} \end{array} \right) $

手順3: 外力条件を与える

外力条件(動画では荷重条件と言っているけど、どっちでもいい) は、すべての節点が壁や隣の要素の節点とかにくっついた状態で、 見える外力だけを与える。 壁から切り離さないと見えない反力や、 要素どうしを切り離さないと見えない節点2の内力（断面力としての軸力）など、 くっつけたときに作用・反作用でプラマイゼロになって見えなくなるものは 外力として与えてはいけない。 つまり、外力は$N_{3}=P$のみで、 それ以外はすべて0である。
$ \left( \begin{array}{c} 0\\ 0\\ P \end{array} \right) = \left( \begin{array}{ccc} k & -k & 0 \\ -k & 2k & -k \\ 0 & -k & k \end{array} \right) \left( \begin{array}{c} w_{1}\\ w_{2}\\ w_{3} \end{array} \right) $

手順4: 境界条件を与える

境界条件は、節点1が壁にくっついているので$w_{1}=0$だが、 1要素のときに説明した 一般的な境界条件の与え方に 従って、以下のように与える。
$ \left( \begin{array}{c} 0\\ 0\\ P \end{array} \right) = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 2k & -k \\ 0 & -k & k \end{array} \right) \left( \begin{array}{c} w_{1}\\ w_{2}\\ w_{3} \end{array} \right) $
これを解いていく。
$0=w_{1}$   これは境界条件が求まっただけ。
$0=2k w_{2}-k w_{3}$
$P=-k w_{2}+k w_{3}$
第2式と第3式を辺々足すと、
$P=k w_{2}$
よって、
$w_{2}=\frac{P}{k}$
これを第2式に代入して、
$w_{3}=\frac{2P}{k}$
と求まる。

手順5: 求めた節点変位を用いて 反力や断面力を求める

求まった節点変位をもとの要素剛性方程式に代入すれば、 各節点を切断した場合の断面力が求まる。 反力とか断面力というのは、節点を切り離さないと見えないので、 ばね要素を節点2で切断し、2つの要素に切り離したときの、 それぞれの要素についての要素剛性方程式を考えることになる。 反力・断面力を求める際に使う剛性方程式は、 全体剛性方程式ではなく、 もとの要素剛性方程式に節点変位を代入する。 つまり、もとの要素剛性方程式
要素①：
$ \left( \begin{array}{c} N_{1}\\ N_{2}^{①} \end{array} \right) = \left( \begin{array}{cc} k & -k\\ -k & k \end{array} \right) \left( \begin{array}{c} w_{1}\\ w_{2} \end{array} \right) $

要素②：
$ \left( \begin{array}{c} N_{2}^{②} \\ N_{3} \end{array} \right) = \left( \begin{array}{cc} k & -k \\ -k & k \end{array} \right) \left( \begin{array}{c} w_{2}\\ w_{3} \end{array} \right) $
に、 $w_{2}=\frac{P}{k},\;\; w_{3}=\frac{2P}{k}$を代入すると、
要素①：
$ \left( \begin{array}{c} N_{1}\\ N_{2}^{①} \end{array} \right) = \left( \begin{array}{cc} k & -k\\ -k & k \end{array} \right) \left( \begin{array}{c} 0 \\ \frac{P}{k} \end{array} \right) = \left( \begin{array}{cc} -P\\ P \end{array} \right) $

要素②：
$ \left( \begin{array}{c} N_{2}^{②} \\ N_{3} \end{array} \right) = \left( \begin{array}{cc} k & -k \\ -k & k \end{array} \right) \left( \begin{array}{c} \frac{P}{k} \\ \frac{2P}{k} \end{array} \right) = \left( \begin{array}{cc} -P\\ P \end{array} \right) $
つまり、
$N_{1}=-P$
$N_{2}^{①}=\;\;P$
$N_{2}^{②}=-P$
$N_{3}=\;\;P$
と求まる。

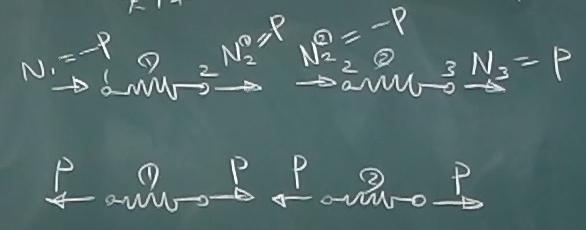これをまず、求まった通りの $N_{1}, N_{2}^{①}, N_{2}^{②}, N_{3}$のまま描いてみる。 そして、それぞれ符号が負になっているものについては、 実際の向きに描き直してやる。 すると、要素①も、要素②も$P$の引張の軸力が生じてつりあっていることがわかる。

例題（2要素）

図のような ばね構造系について、 (1)剛性方程式を用いて節点変位を求め、 (2)求めた節点変位を用いて反力・断面力を求め、 (3)ばね要素の各節点に作用する力を、正の値で描ける向きに矢印を向けて図示せよ。

こたえは、節点変位：ここ、 反力・断面力： ここ。 解説の動画はここ。

2022年度小テスト： 問題, 解答
2021年度小テスト： 問題, 解答
2020年度小テスト： 問1, 問2, 問3, 解答