
構造力学(マトリクス構造解析)目次
(授業動画)
小さい字は補足説明なので、読み飛ばしてもいいです。
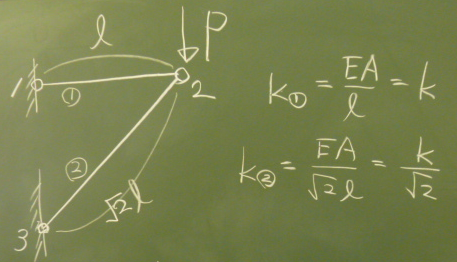 図のような2要素のトラスの例題を解いてみたい。
トラスは最低3要素ないとトラスと言わないのではないかとか、
反力が4個で求まらないのではないかとか、その辺の細かいことは
置いておく。
要は、なるべく簡単な2要素の問題を ばね要素(トラス要素)の
剛性方程式で解いてみるという趣旨だ。
剛性方程式で解く前に、
まずは部材力と節点変位の正解を求めておこう。
反力は4個だが、
ためしに内的静定・不静定を
判定してみると、部材数$m=2$, 反力数$r=4$, 節点数$j=3$で、
$m+r-2j=2+4-2\times 3=0$で内的静定だ。
というわけで、たぶん部材力は求まりそうだ。
トラス要素①も②も、同じ材料、同じ断面で伸び剛性は$EA$
とする。そうすると、
要素①のばね定数は、$k_{①}=\frac{EA}{\ell}$となるので、
これを$k$とすると、
要素②のばね定数は、$k_{②}=\frac{EA}{\sqrt{2}\ell}=\frac{k}{\sqrt{2}}$となる。
図のような2要素のトラスの例題を解いてみたい。
トラスは最低3要素ないとトラスと言わないのではないかとか、
反力が4個で求まらないのではないかとか、その辺の細かいことは
置いておく。
要は、なるべく簡単な2要素の問題を ばね要素(トラス要素)の
剛性方程式で解いてみるという趣旨だ。
剛性方程式で解く前に、
まずは部材力と節点変位の正解を求めておこう。
反力は4個だが、
ためしに内的静定・不静定を
判定してみると、部材数$m=2$, 反力数$r=4$, 節点数$j=3$で、
$m+r-2j=2+4-2\times 3=0$で内的静定だ。
というわけで、たぶん部材力は求まりそうだ。
トラス要素①も②も、同じ材料、同じ断面で伸び剛性は$EA$
とする。そうすると、
要素①のばね定数は、$k_{①}=\frac{EA}{\ell}$となるので、
これを$k$とすると、
要素②のばね定数は、$k_{②}=\frac{EA}{\sqrt{2}\ell}=\frac{k}{\sqrt{2}}$となる。
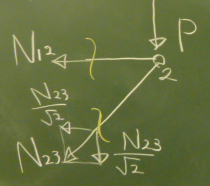 図のように2要素をそれぞれ切断し、(反力を使わなくていい)右側の
ピースを取り出す。
図のように2要素をそれぞれ切断し、(反力を使わなくていい)右側の
ピースを取り出す。
$\Sigma\downarrow=P+\frac{N_{23}}{\sqrt{2}}=0$
$\Sigma\rightarrow=-N_{12}-\frac{N_{23}}{\sqrt{2}}=0$
$N_{23}=-\sqrt{2}P$
$N_{12}=P$
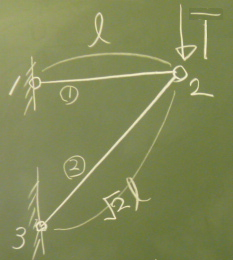 単位荷重法で、
まずは節点2の下($y$)方向の変位を求める。
節点2の下方向に
仮想単位荷重$\overline{1}$を与えて、部材力を求める。
仮想の(うその)荷重だということを強調するために、$\overline{1}$と
バーをつけているが、単なる単位荷重$1$である。
上で求めた部材力の$P$に$1$を代入すればいいだけだから、
仮想部材力は、
単位荷重法で、
まずは節点2の下($y$)方向の変位を求める。
節点2の下方向に
仮想単位荷重$\overline{1}$を与えて、部材力を求める。
仮想の(うその)荷重だということを強調するために、$\overline{1}$と
バーをつけているが、単なる単位荷重$1$である。
上で求めた部材力の$P$に$1$を代入すればいいだけだから、
仮想部材力は、
$\overline{N}_{23}=-\sqrt{2}$
$\overline{N}_{12}=1$
そうすると、節点2の下方向変位$v_{2}$は、
公式から、
$$\overline{1}\cdot v_{2}
=\int_{全部材}\frac{N\overline{N}}{EA}dz^{\ell}$$
すべての部材について、$N$と$\overline{N}$をかけて、
それぞれの軸に沿って端から端まで
(要は、要素が横たわっている局所系の$z^{\ell}$に沿って)
その要素の長さぶんの積分をすればいいのだけど、
トラスの部材力というのは、
それぞれの部材について、端から端まで同じ値だから、
端から端まで積分するというのは、単にその要素の長さをかければいいことになる。
つまり、
$$\overline{1}\cdot v_{2}
=\int_{全部材}\frac{N\overline{N}}{EA}dz^{\ell}$$
$$=\frac{1}{EA}
\left(N_{12}\overline{N}_{12}\ell +N_{23}\overline{N}_{23}\cdot\sqrt{2}\ell
\right)$$
$$=\frac{1}{EA}
\left(P\cdot 1\cdot\ell +(-\sqrt{2}P)(-\sqrt{2})\cdot \sqrt{2}\ell
\right)$$
$$=(1+2\sqrt{2})\frac{P\ell}{EA}=(1+2\sqrt{2})\frac{P}{k}$$
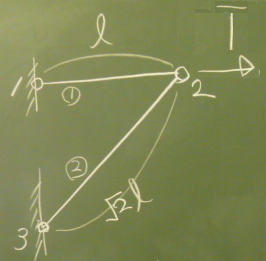 次に、節点2の右($z$)方向変位$w_{2}$も
求めておく。節点2に右方向の仮想単位荷重
$\overline{1}$を与えて、部材力を求める。
次に、節点2の右($z$)方向変位$w_{2}$も
求めておく。節点2に右方向の仮想単位荷重
$\overline{1}$を与えて、部材力を求める。
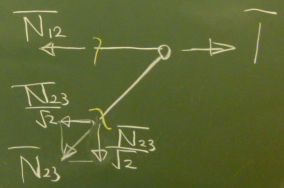 さきほどと同様に要素を2箇所で切って、
(反力を考えなくていい)右側のピースを取り出す。
さきほどと同様に要素を2箇所で切って、
(反力を考えなくていい)右側のピースを取り出す。
$\Sigma\rightarrow=-\overline{N}_{12}+1
-\frac{\overline{N}_{23}}{\sqrt{2}}=0$
$\Sigma\downarrow=\frac{\overline{N}_{23}}{\sqrt{2}}=0$
$\overline{N}_{12}=1$
$\overline{N}_{23}=0$
あとは、公式に従ってもとの構造(下向きの$P$が節点2に作用している)の部材力$N$と
今回の仮想構造(右向きの$1$が節点2に作用している)
の部材力$\overline{N}$をかけて積分すればよい。
$$\overline{1}\cdot w_{2}
=\int_{全部材}\frac{N\overline{N}}{EA}dz^{\ell}$$
$$=\frac{1}{EA}
\left(N_{12}\overline{N}_{12}\ell +N_{23}\overline{N}_{23}\cdot\sqrt{2}\ell
\right)$$
$$=\frac{1}{EA}\left(P\cdot 1\cdot\ell + (-\sqrt{2}P)\cdot 0 \cdot\sqrt{2}\ell
\right)$$
$$=\frac{P\ell}{EA}=\frac{P}{k}$$
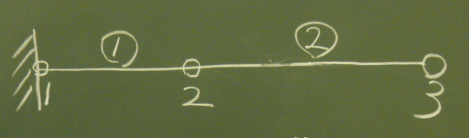 では、次に、この2要素トラスを剛性方程式で解いてみる。
まずは、全体系の要素剛性方程式を作る前に、
すべてのばね要素を全体系($yz$系)の$z$軸に横たわらせ
(これを仮に初期状態と呼ぶことにするが)、
初期状態で、節点1が左に来るのか右に来るのか、
節点2が左に来るのか右に来るのか....をすべての要素について決めてしまう。
要素の並べ順や節点の右左は、ある意味どう並べても
解けるとは思うが(後で、プログラムを使った実習の際に、
わざと変な並べ方にして解けるかどうか、同じ答えが出るかどうか
試してみてほしい)、手で解く際には、なるべく
マトリクスがきれいになって、簡単に解ける方がいい。
そうすると、
各要素は、なるべく1直線につながるように並べて、
節点はなるべく左から順番につけていった方が、マトリクスの
重ね合わせが楽である。
というわけで、図のように、初期状態で要素①、要素②は、
図のように$z$軸上に左から要素①、要素②の順でつながって横たわり、
節点は、左から1, 2, 3と並んでいることにする。
では、次に、この2要素トラスを剛性方程式で解いてみる。
まずは、全体系の要素剛性方程式を作る前に、
すべてのばね要素を全体系($yz$系)の$z$軸に横たわらせ
(これを仮に初期状態と呼ぶことにするが)、
初期状態で、節点1が左に来るのか右に来るのか、
節点2が左に来るのか右に来るのか....をすべての要素について決めてしまう。
要素の並べ順や節点の右左は、ある意味どう並べても
解けるとは思うが(後で、プログラムを使った実習の際に、
わざと変な並べ方にして解けるかどうか、同じ答えが出るかどうか
試してみてほしい)、手で解く際には、なるべく
マトリクスがきれいになって、簡単に解ける方がいい。
そうすると、
各要素は、なるべく1直線につながるように並べて、
節点はなるべく左から順番につけていった方が、マトリクスの
重ね合わせが楽である。
というわけで、図のように、初期状態で要素①、要素②は、
図のように$z$軸上に左から要素①、要素②の順でつながって横たわり、
節点は、左から1, 2, 3と並んでいることにする。
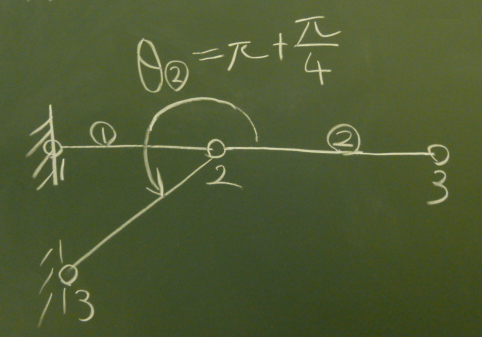 この初期状態から問題の2要素トラスをつくるには、
要素①はそのままで回転する必要はなく、
つまり$\theta_{①}=0$である。
一方、要素②は回転させる必要があるが、
その際、初期状態で$z$軸に横たわる要素②の左節点を中心にして、
$x軸$右ねじまわり(つまり反時計回り)に
$\theta_{②}$だけ、所定の位置まで回転させる。
そうすれば、全体系から$\theta_{②}$回転した局所系($y^{\ell}z^{\ell}$系)
で、$z^{\ell}$に横たわる局所系の要素剛性方程式が成り立つ。
初期状態の要素②を左節点(節点2)を中心に$x軸$右ねじまわりに回転させて、
問題の2要素トラスの位置まで持ってくるには、
$\theta_{②}=180^{\circ}+45^{\circ}=\pi+\frac{\pi}{4}$とすればよい。
この初期状態から問題の2要素トラスをつくるには、
要素①はそのままで回転する必要はなく、
つまり$\theta_{①}=0$である。
一方、要素②は回転させる必要があるが、
その際、初期状態で$z$軸に横たわる要素②の左節点を中心にして、
$x軸$右ねじまわり(つまり反時計回り)に
$\theta_{②}$だけ、所定の位置まで回転させる。
そうすれば、全体系から$\theta_{②}$回転した局所系($y^{\ell}z^{\ell}$系)
で、$z^{\ell}$に横たわる局所系の要素剛性方程式が成り立つ。
初期状態の要素②を左節点(節点2)を中心に$x軸$右ねじまわりに回転させて、
問題の2要素トラスの位置まで持ってくるには、
$\theta_{②}=180^{\circ}+45^{\circ}=\pi+\frac{\pi}{4}$とすればよい。
①の全体系の要素剛性方程式は、
$\theta_{①}=0$だから、座標変換行列は単位行列になり、
マトリクス部分は、
局所系の要素剛性方程式と同じになる。
節点2の節点力は、要素①と要素②に分配されるから、
要素①の要素剛性方程式は、要素①に分配される方という意味で①の上付き添字をつける。
要素①の全体系の要素剛性方程式
$
\left(
\begin{array}{c}
S_{1}\\
N_{1}\\
S_{2}^{①}\\
N_{2}^{①}
\end{array}
\right)
=
\left(
\begin{array}{rrrr}
0 & 0 & 0 & 0 \\
0 & k & 0 & -k \\
0 & 0 & 0 & 0 \\
0 & -k & 0 & k
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}\\
w_{1}\\
v_{2}\\
w_{2}
\end{array}
\right)
$
一方、要素②は、
$\theta_{②}=\pi+\frac{\pi}{4}$だから、
座標変換行列は、
$\sin(\phi+\pi)=-\sin\phi$,
$\cos(\phi+\pi)=-\cos\phi$の関係を用いて、以下のようになる。
$
\mathbf{T}=
\left(
\begin{array}{rr}
\cos(\frac{\pi}{4}+\pi) & \sin(\frac{\pi}{4}+\pi) \\
-\sin(\frac{\pi}{4}+\pi) & \cos(\frac{\pi}{4}+\pi)
\end{array}
\right)
=
\left(
\begin{array}{rr}
-\cos(\frac{\pi}{4}) & -\sin(\frac{\pi}{4}) \\
\sin(\frac{\pi}{4}) & -\cos(\frac{\pi}{4})
\end{array}
\right)
=
\left(
\begin{array}{rr}
-\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{array}
\right)
$
$
\mathbf{T}^{T}=
\left(
\begin{array}{rr}
-\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
-\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{array}
\right)
$
よって、要素②の全体系の要素剛性方程式は、以下のようになる。
要素②の全体系の要素剛性方程式
$
\left(
\begin{array}{c}
S_{2}^{②}\\
N_{2}^{②}\\
S_{3}\\
N_{3}
\end{array}
\right)
=
\left(
\begin{array}{rrrr}
-\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 & 0 \\
-\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 & 0 \\
0 & 0 & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
0 & 0 & -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{array}
\right)
%
\left(
\begin{array}{rrrr}
0 & 0 & 0 & 0 \\
0 & \frac{k}{\sqrt{2}} & 0 & -\frac{k}{\sqrt{2}} \\
0 & 0 & 0 & 0 \\
0 & -\frac{k}{\sqrt{2}} & 0 & \frac{k}{\sqrt{2}}
\end{array}
\right)
\left(
\begin{array}{rrrr}
-\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 & 0 \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} & 0 & 0 \\
0 & 0 & -\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
0 & 0 & \frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}}
\end{array}
\right)
\left(
\begin{array}{c}
v_{2}\\
w_{2}\\
v_{3}\\
w_{3}
\end{array}
\right)
$
マトリクス3個を手でかけ合わせるのはちょっと大変だが、
これを計算すると、以下のようになる。
$
\left(
\begin{array}{c}
S_{2}^{②}\\
N_{2}^{②}\\
S_{3}\\
N_{3}
\end{array}
\right)
=
\frac{k}{2\sqrt{2}}
\left(
\begin{array}{rrrr}
1 & -1 & -1 & 1 \\
-1 & 1 & 1 & -1 \\
-1 & 1 & 1 & -1 \\
1 & -1 & -1 & 1
\end{array}
\right)
\left(
\begin{array}{c}
v_{2}\\
w_{2}\\
v_{3}\\
w_{3}
\end{array}
\right)
$
さて、要素①と要素②の要素剛性方程式ができたので、
これらを第2回の2要素の重ね合わせの要領で、
重ね合わせて全体剛性方程式を組み立てると、以下のようになる。
要素①の伸び剛性の成分は$k$だが、マトリクス全体を$\frac{k}{2\sqrt{2}}$でくくった
ので、要素①のマトリクス内の成分は$2\sqrt{2}$となっている。
全体剛性方程式
$
\left(
\begin{array}{c}
S_{1}\\
N_{1}\\
S_{2}\\
N_{2}\\
S_{3}\\
N_{3}
\end{array}
\right)
=
\frac{k}{2\sqrt{2}}
\left(
\begin{array}{rrrrrr}
0 & 0 & 0 & 0 & 0 & 0 \\
0 & 2\sqrt{2} & 0 & -2\sqrt{2} & 0 & 0 \\
0 & 0 & 1 & -1 & -1 & 1 \\
0 & -2\sqrt{2} & -1 & 2\sqrt{2}+1 & 1 & -1 \\
0 & 0 & -1 & 1 & 1 & -1 \\
0 & 0 & 1 & -1 & -1 & 1
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}\\
w_{1}\\
v_{2}\\
w_{2}\\
v_{3}\\
w_{3}
\end{array}
\right)
$
さて、外力条件は、節点2の下方向に外力$P$が作用しているから、
$S_{2}=P$, それ以外はすべてゼロ。
境界条件は、節点1と3が固定だから、$v_{1}=w_{1}=v_{3}=w_{3}=0$.
これらを上記の全体剛性方程式に適用し、
第1回の一般的な境界条件の与え方の要領で境界条件を与えると、
以下のようになる。
$
\left(
\begin{array}{c}
0\\
0\\
P\\
0\\
0\\
0
\end{array}
\right)
=
\frac{k}{2\sqrt{2}}
\left(
\begin{array}{rrrrrr}
1 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & -1 & 0 & 0 \\
0 & 0 & -1 & 2\sqrt{2}+1 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 1
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}\\
w_{1}\\
v_{2}\\
w_{2}\\
v_{3}\\
w_{3}
\end{array}
\right)
$
つまり、3行目と4行目だけ連立させて解けばいいことになるが、
両辺に$\frac{2\sqrt{2}}{k}$をかけてから展開すると、
$2\sqrt{2}\frac{P}{k}=v_{2}-w_{2}$
$0=-v_{2}+(2\sqrt{2}+1)w_{2}$
辺々足すと、
$2\sqrt{2}\frac{P}{k}=2\sqrt{2}w_{2}$だから、
$w_{2}=\frac{P}{k}$
これを、3行目の式に代入して、
$v_{2}=(1+2\sqrt{2})\frac{P}{k}$
というわけで、上で単位荷重法で求めた正解と同じ変位が求まった。
では、これらの変位を用いて、
部材力を求めてみる。
部材力というのは、内力であり、
トラス要素の節点の近傍を切断して、要素を1個ずつ取り出したときの
切断面に作用している節点力と考えられるから、
求まった節点変位を、全体系の要素剛性方程式に代入して求める。
全体剛性方程式に代入してはいけない。
では、代入してみる。
要素①の要素剛性方程式に節点変位を代入
$
\left(
\begin{array}{c}
S_{1}\\
N_{1}\\
S_{2}^{①}\\
N_{2}^{①}
\end{array}
\right)
=
\left(
\begin{array}{rrrr}
0 & 0 & 0 & 0 \\
0 & k & 0 & -k \\
0 & 0 & 0 & 0 \\
0 & -k & 0 & k
\end{array}
\right)
\left(
\begin{array}{c}
0\\
0\\
(1+2\sqrt{2})\frac{P}{k}\\
\frac{P}{k}
\end{array}
\right)
=
\left(
\begin{array}{c}
0\\
-P\\
0 \\
P
\end{array}
\right)
$
要素②の要素剛性方程式に節点変位を代入
$
\left(
\begin{array}{c}
S_{2}^{②}\\
N_{2}^{②}\\
S_{3}\\
N_{3}
\end{array}
\right)
=
\frac{k}{2\sqrt{2}}
\left(
\begin{array}{rrrr}
1 & -1 & -1 & 1 \\
-1 & 1 & 1 & -1 \\
-1 & 1 & 1 & -1 \\
1 & -1 & -1 & 1
\end{array}
\right)
\left(
\begin{array}{c}
(1+2\sqrt{2})\frac{P}{k}\\
\frac{P}{k}\\
0\\
0
\end{array}
\right)
=
\left(
\begin{array}{c}
P\\
-P\\
-P \\
P
\end{array}
\right)
$
 要素①と要素②を節点の近傍で切り離して、ばらばらに描き、
それらの切断面に求まった節点力($N_{1}$とか$S_{2}^{①}$とか)をまず
求まった通りに描いたのが図の左側。
マイナスに求まった節点力を逆向きの矢印にして、実際の向きで描いたのが図の右側。
つまり、要素①は$P$の引張力が作用し、
要素②は鉛直、水平にそれぞれ$P$の力の合力で、軸方向には
$\sqrt{2}P$の圧縮力が作用していることになる。
冒頭で要素を切断して力のつりあいで求めた
$N_{12}=P, \ N_{23}=-\sqrt{2}P$とも一致している。
要素①と要素②を節点の近傍で切り離して、ばらばらに描き、
それらの切断面に求まった節点力($N_{1}$とか$S_{2}^{①}$とか)をまず
求まった通りに描いたのが図の左側。
マイナスに求まった節点力を逆向きの矢印にして、実際の向きで描いたのが図の右側。
つまり、要素①は$P$の引張力が作用し、
要素②は鉛直、水平にそれぞれ$P$の力の合力で、軸方向には
$\sqrt{2}P$の圧縮力が作用していることになる。
冒頭で要素を切断して力のつりあいで求めた
$N_{12}=P, \ N_{23}=-\sqrt{2}P$とも一致している。
マトリクスを使わずに、力のつりあいや単位荷重法で
手計算でトラスを解く場合、普通は、まず反力とか部材力や断面力を求めて、
それから変位を求めるという手順になるのが普通だが、
剛性マトリクスを用いた解法の場合、
通常は、節点変位を未知数として解いているので、まずは節点変位が求まり、
この求まった節点変位を要素剛性方程式に代入して断面力を求めるという逆の手順になる。
トラスの複数要素とかになってくると、さすがにマトリクスを何個もかけたり重ね合わせたりを 手計算でやるのは大変になってくるので、その辺のやり方は、 理屈を理解した上で、後でプログラムで計算できればいいことにして、 今回は、後でプログラムで計算する際に正解がわからないと困るので、 単位荷重法でトラスの節点変位を求める問題を例題とする。 小テストでもこのような問題を出題することにする。
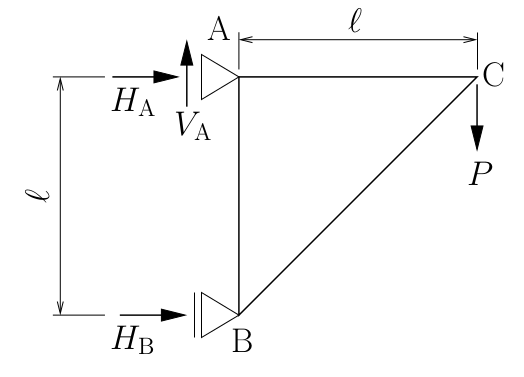 節点Cの鉛直下方向変位、水平右方向変位を求めよ。
ただし、すべての部材の伸び剛性は$EA$とする。
節点Cの鉛直下方向変位、水平右方向変位を求めよ。
ただし、すべての部材の伸び剛性は$EA$とする。
右の図は、
2017年度の構造力学IIの定期試験の問題なので、
みなさんは既に問題なく解けることとは思うが、
念のため、復習しておいてほしい。
答えは、
ここ。
上の2要素トラスと似ているが、部材ABにも部材力が発生するので、
答えは変わってくる。
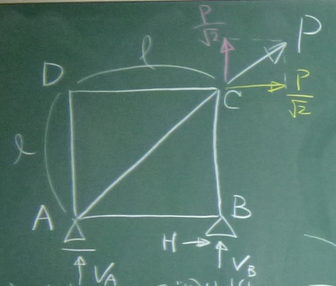 点Cの荷重方向(つまり右上$45^{\circ}$方向)の変位を求めよ。
すべての部材の伸び剛性は$EA$とする。
答えは
ここ。
点Cの荷重方向(つまり右上$45^{\circ}$方向)の変位を求めよ。
すべての部材の伸び剛性は$EA$とする。
答えは
ここ。
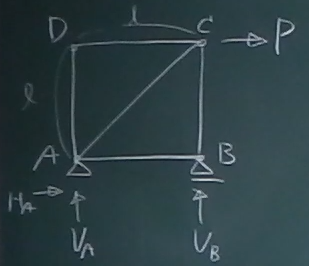 点Cの鉛直変位、水平変位を求めよ。
すべての部材の伸び剛性は$EA$とする。
答えの動画解説はここ
点Cの鉛直変位、水平変位を求めよ。
すべての部材の伸び剛性は$EA$とする。
答えの動画解説はここ
2022年度 小テスト第5回:
問,
解答
2021年度 小テスト第5回:
問,
解答
2020年度 小テスト第5回:
問1,
問2,
解答