
構造力学(応用)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
 細長い棒を押していくと
(まあ、最初のうちはフックの法則に従って、軸方向に縮んでいるのかも
しれないが、ある荷重に達すると)
写真のように「ぐにゃっ」と曲がる。
これは、棒を曲げて(例えば、棒の両端を持ってモーメントをかけて)曲がっている
のではなく、あくまで、棒の軸方向にしか力を加えていなくても、
ある荷重に達すると、棒は、軸方向だけに縮むことに耐えられなくなり、
「ぐにゃっ」と曲がるのである。
こういう現象を「
細長い棒を押していくと
(まあ、最初のうちはフックの法則に従って、軸方向に縮んでいるのかも
しれないが、ある荷重に達すると)
写真のように「ぐにゃっ」と曲がる。
これは、棒を曲げて(例えば、棒の両端を持ってモーメントをかけて)曲がっている
のではなく、あくまで、棒の軸方向にしか力を加えていなくても、
ある荷重に達すると、棒は、軸方向だけに縮むことに耐えられなくなり、
「ぐにゃっ」と曲がるのである。
こういう現象を「
このように棒の軸方向に圧縮を加えて生じる座屈を
柱のオイラー座屈というが、
この他にも、プラスチックのものさしとか、細長い板を、
板の平面内で曲げようとすると、ねじれてその平面から飛び出そうとする
横ねじれ座屈や、傘が裏返ったりヘアピンみたいに2つのつりあい状態を
ペコペコと行ったり来たりする飛び移り座屈など、座屈には様々な種類がある。
さて、
棒にどれくらいの荷重を加えると座屈するかというのを、
これまで学んできた構造力学の知識を用いて導くことができるだろうか?
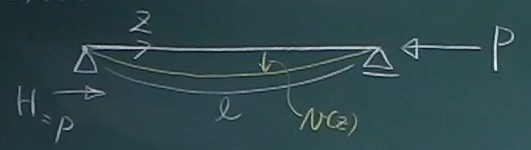 まずは、図のような単純梁のローラー支承側を荷重$P$で押してやり、
$P$を少しずつ大きくしていくとしよう。
荷重が十分に小さい最初のうちは、フックの法則に従って、
梁は、軸方向だけに$\delta$だけ縮んでるはずだ。
梁の伸び剛性を$EA$とすれば、梁のばね定数は
$\frac{EA}{\ell}$だから、
フックの法則から、$P=\frac{EA}{\ell}\delta$の関係が成り立つ。
しかし、荷重がある大きさに達した途端、
梁が座屈して、上または下方向(今回は、下方向にしておこう)に$v(z)$だけ
たわんだものとしよう
(実際の梁では、初期不整があるので、
ある荷重で突然 座屈するのではなく、
ある荷重に近づくに連れて、どんどんたわみが大きくなっていく)。
この座屈したときの荷重$P$とたわみ$v(z)$の関係はどうなっているのだろうか。
まずは、構造力学Iのやり方で力のつりあいを考えてみる。
左端の反力は、力のつりあいから、
右向きに$P$の水平反力だけになる。
まずは、図のような単純梁のローラー支承側を荷重$P$で押してやり、
$P$を少しずつ大きくしていくとしよう。
荷重が十分に小さい最初のうちは、フックの法則に従って、
梁は、軸方向だけに$\delta$だけ縮んでるはずだ。
梁の伸び剛性を$EA$とすれば、梁のばね定数は
$\frac{EA}{\ell}$だから、
フックの法則から、$P=\frac{EA}{\ell}\delta$の関係が成り立つ。
しかし、荷重がある大きさに達した途端、
梁が座屈して、上または下方向(今回は、下方向にしておこう)に$v(z)$だけ
たわんだものとしよう
(実際の梁では、初期不整があるので、
ある荷重で突然 座屈するのではなく、
ある荷重に近づくに連れて、どんどんたわみが大きくなっていく)。
この座屈したときの荷重$P$とたわみ$v(z)$の関係はどうなっているのだろうか。
まずは、構造力学Iのやり方で力のつりあいを考えてみる。
左端の反力は、力のつりあいから、
右向きに$P$の水平反力だけになる。
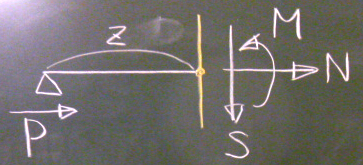 断面力がどうなるかについては、任意点で梁を切断し、
例えば左側のピースを取り出して、つりあいを考えてみる。
断面力がどうなるかについては、任意点で梁を切断し、
例えば左側のピースを取り出して、つりあいを考えてみる。
$\sum\downarrow=S=0$ つまり、$S(z)=0$
$\sum\rightarrow=P+N=0$ つまり、$N(z)=-P$で一定の圧縮力が作用している。
$\sum_{z}\circlearrowleft=M=0$ つまり、$M(z)=0$
左端の$P$の作用点は梁の軸線上だから、切断点($z$点)回りにはモーメントを作らない。
$M(z)=-EIv''(z)$が$0$ということは、
2回積分すると、$v(z)=Az+B$となる。
境界条件の$v(0)=0$と$v(\ell)=0$から、
$v(0)=B=0$, よって$v(\ell)=A\ell=0$となり、$A=B=0$なので、
結局$v(z)=0$となる。
2023/2/1まで、
「$M(z)=-EIv''(z)$が$0$ということは、
これを積分しても$v(z)$は$0$だから、」と書いていたが、
それは正確ではないし、ミスリーディングでした。
すいません。
梁はたわんでいないということだ。
つまり、$N(z)=-P$, $S(z)=M(z)=0$という答えは、
梁がたわまずに、フックの法則に従って、
軸線に沿って、どこまでも縮み続ける場合のつりあいを表したものだ。
でも、我々が知りたいのは、そういうつりあい状態ではなくて、
梁が座屈して、たわみ$v(z)$が発生している状態だ。
なので、梁が座屈して$v(z)$のたわみが発生したものとして、
変形後のつりあいを考えてみる。
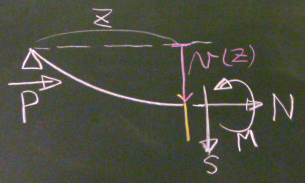 鉛直方向のつりあい:$\sum\downarrow=S=0$ つまり、$S(z)=0$
鉛直方向のつりあい:$\sum\downarrow=S=0$ つまり、$S(z)=0$
水平方向のつりあい:$\sum\rightarrow=P+N=0$ つまり、$N(z)=-P$
に関しては、初期状態の梁を切断して つりあいを考えた場合と同じだ。
しかし、切断点($z$点)回りのモーメントのつりあいに関しては、
左端の水平反力の作用線(ヒンジ支承の下に描いているけど、
実際の作用線は、初期状態の軸線に沿っている)は、
たわんだ切断点から$v(z)$だけ離れているから、
この水平反力$P$は、右回りに$P\cdot v(z)$のモーメントをつくる。すると、
モーメントのつりあい:
$\sum_{z}\circlearrowleft=-P\cdot v(z)+M=0$ つまり、
$M(z)=Pv(z)$となる。
これに$M(z)=-EIv''(z)$を代入すれば、$-EIv''(z)=Pv(z)$となる。
$(z)$を省略して、変形すると、
${\displaystyle v''+\frac{P}{EI}v=0}$
と書ける。これはなんか、基礎教育科目の数学のどれかに出てきた
典型的な微分方程式のようだ。より微分方程式っぽく見えるように、
$\alpha^{2}=\frac{P}{EI}$と置いてみると、以下のようになる。
$v''=-\alpha^{2}v$
ちゃんとした解き方($y=e^{\lambda z}$とおいて$\lambda$を求めるみたいな)は、
数学の教科書を見てもらうとして、
これの一般解は、$A, B$を定数として以下のようになる。
$v(z)=A\sin\alpha z+B\cos\alpha z$
確認のため、2回 微分してみると、
$v'(z)=\alpha A\cos\alpha z-\alpha B\sin\alpha z$
$v''(z)=-\alpha^{2} A\sin\alpha z-\alpha^{2} B\cos\alpha z$
となり、$v''=-\alpha^{2}v$を満たす。
未知数は、$A$, $B$の2つであるが、
境界条件も$v(0)=0$と$v(\ell)=0$の2つが使えるので、
$A$, $B$が決まるかも知れない。
まず、$v(0)=0$から、
$v(0)=B=0$ ということで$B$は$0$だ。
次に、$v(\ell)=0$から、
$v(\ell)=A\sin\alpha\ell=0$
つまり、$A=0$ または $\sin\alpha\ell=0$ となる。
$A=0$のときは、$v(z)=0$となるから、これはたわみが発生せずに、
梁が軸に沿って(フックの法則に従って)縮み続ける解だ。
こういう当たり前の解のことを「自明解」と言う。
でも、我々が知りたい座屈する方の解はこれではない。
では、$\sin\alpha\ell=0$のときは、どうだろうか。
$\sin\theta=0$となるのは、$\theta=n\pi\;\;\;\;(n=1,2,3,....)$のときだから、
$\alpha\ell=n\pi\;\;\;\;(n=1,2,3,....)$
となる。つまり、${\displaystyle \alpha=\frac{n\pi}{\ell}}$だから、
${\displaystyle \alpha^{2}=\left(\frac{n\pi}{\ell}\right)^{2}\;\;\;\;(n=1,2,3,....)}$
となる。
${\displaystyle \alpha^{2}=\frac{P}{EI}}$だったから、
これを代入すると、以下のようになる。
${\displaystyle P=\left(\frac{n\pi}{\ell}\right)^{2}EI\;\;\;\;(n=1,2,3,....)}$
実は、単純梁を軸方向に押した場合、この$P$が座屈を起こす荷重
(座屈荷重)となる。
座屈は英語では buckling と言うが、座屈荷重を記号で書くときは、
限界荷重(critical load)という意味で、$P_{cr}$と書くことが多い。
この式はオイラーが導いているので(たぶん)、
オイラーの座屈公式などと呼ばれる。
${\displaystyle P_{cr}=\left(\frac{n\pi}{\ell}\right)^{2}EI\;\;\;\;(n=1,2,3,....)}\;\;\;\;\;$
(重要)
$\alpha=\dfrac{n\pi}{\ell}$を$v(z)$の式に代入すると、
$v(z)=A\sin\dfrac{n\pi z}{\ell}$
となる。$A$は不定だが、座屈形状が$\sin$波で表されることを示している。
この座屈の問題は微分方程式の固有値問題に
なっていて、$\frac{P}{EI}$が固有値に対応し、$v(z)$が固有関数に対応している。
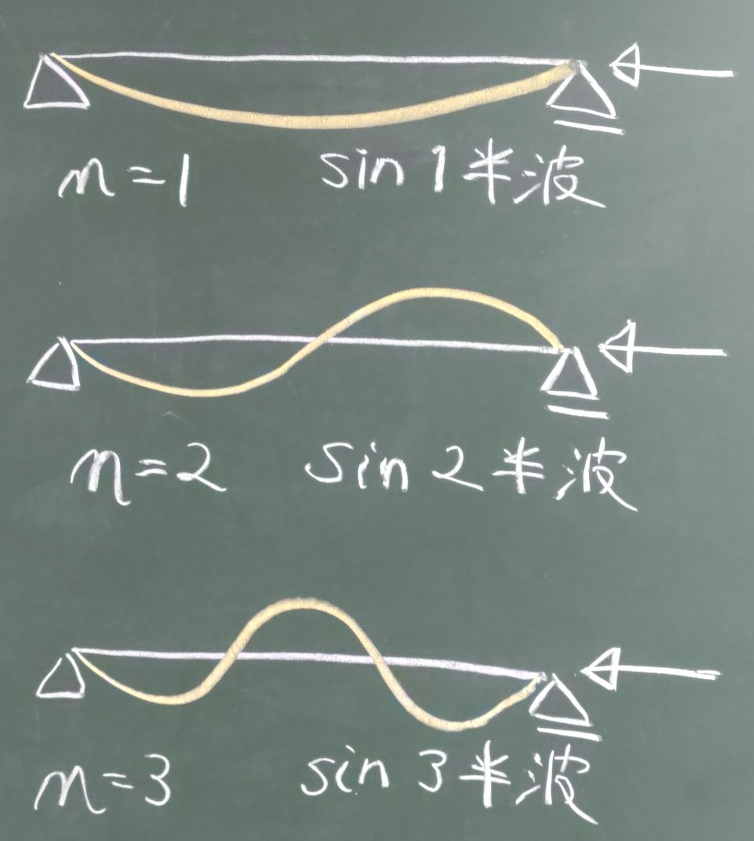 $n=1$というのは正弦波の山が1個ぶんで座屈する状態、
$n=2$というのは 正弦波の山が2個ぶんで座屈する状態
($n=3$以降も同様)に対応している。
山1個は、正弦波の1サイクル($0\le\theta\le 2\pi$)の半分なので、
正弦波の山1個ぶんを表すときは、「sin 1 半波(さいん いち はんぱ)」
とか、
山2個ぶんを表すときは、「sin 2 半波(さいん に はんぱ)」
と言ったりする。
このような座屈形状のことを座屈モードと言い、
$n=1,2,3,...$に対応して1次モード、2次モードと言ったりする。
座屈形状は、弦の振動における振動形状に似ているが、
振動の問題でも同じように振動モードという言葉を使う。
柱のオイラー座屈では、$n=1$のときの座屈荷重が最も小さいので、
実際の柱は1次モードで座屈する。
ただし、板の座屈などでは、板の縦横の比率等により、
次数の高いモードの座屈荷重の方が小さくなることもある。
そのような場合、実際の構造物は、最も小さい座屈荷重のモードで
座屈する。
なお、構造解析ソフトウェアなどでは、
固有値解析により求まった座屈荷重を小さい順に並べて、
小さい順から $n=1, 2, 3,...$とするものもあったりする
かもしれないので、
$n=1, 2, 3,...$が、
モードのsin 1 半波数(半波数が1,2,3,..とならない場合はその小さい順)を
表すものなのか、
荷重の小さい順なのかなど、注意が必要である。
$n=1$というのは正弦波の山が1個ぶんで座屈する状態、
$n=2$というのは 正弦波の山が2個ぶんで座屈する状態
($n=3$以降も同様)に対応している。
山1個は、正弦波の1サイクル($0\le\theta\le 2\pi$)の半分なので、
正弦波の山1個ぶんを表すときは、「sin 1 半波(さいん いち はんぱ)」
とか、
山2個ぶんを表すときは、「sin 2 半波(さいん に はんぱ)」
と言ったりする。
このような座屈形状のことを座屈モードと言い、
$n=1,2,3,...$に対応して1次モード、2次モードと言ったりする。
座屈形状は、弦の振動における振動形状に似ているが、
振動の問題でも同じように振動モードという言葉を使う。
柱のオイラー座屈では、$n=1$のときの座屈荷重が最も小さいので、
実際の柱は1次モードで座屈する。
ただし、板の座屈などでは、板の縦横の比率等により、
次数の高いモードの座屈荷重の方が小さくなることもある。
そのような場合、実際の構造物は、最も小さい座屈荷重のモードで
座屈する。
なお、構造解析ソフトウェアなどでは、
固有値解析により求まった座屈荷重を小さい順に並べて、
小さい順から $n=1, 2, 3,...$とするものもあったりする
かもしれないので、
$n=1, 2, 3,...$が、
モードのsin 1 半波数(半波数が1,2,3,..とならない場合はその小さい順)を
表すものなのか、
荷重の小さい順なのかなど、注意が必要である。
 今まで、単純梁が軸方向に圧縮を受ける際の座屈の話をしてきたが、
柱のオイラー座屈 は、片持ち梁とか、他の様々な境界条件でも発生する。
ただし、座屈モードは境界条件によって変わってくるし、
そうすると当然、座屈荷重も変わってくる。
例えば、片持ち梁の先端を軸方向に押していって座屈した場合、
図のように、
片持ち梁のたわみ形状と同じように、固定端側はたわみ角が0になって、
自由端側に最大変位が発生する。
この座屈が発生する座屈荷重を求めるには、
上で単純梁に対する座屈荷重を求めるのと同じようにして、
境界条件を変えればいいとは思うが、
実は、様々な境界条件で生じる座屈モードは、
単純梁の座屈モードの一部になっている
(あるいは単純梁の座屈モードの方が一部になっている)と
考えることによって、単純梁の座屈公式を流用して座屈荷重を求めることができる。
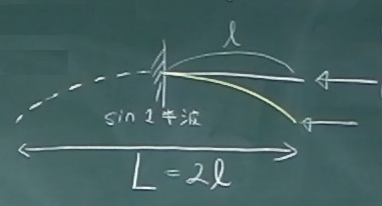
例えば、図のような長さ$\ell$の片持ち梁の場合、
これは、長さ$L=2\ell$の単純梁の1次の座屈モードのちょうど半分と考えれば、
長さ$L=2\ell$の単純梁の座屈荷重と同じだと考えることができる。
つまり、単純梁のオイラーの座屈公式から、
今まで、単純梁が軸方向に圧縮を受ける際の座屈の話をしてきたが、
柱のオイラー座屈 は、片持ち梁とか、他の様々な境界条件でも発生する。
ただし、座屈モードは境界条件によって変わってくるし、
そうすると当然、座屈荷重も変わってくる。
例えば、片持ち梁の先端を軸方向に押していって座屈した場合、
図のように、
片持ち梁のたわみ形状と同じように、固定端側はたわみ角が0になって、
自由端側に最大変位が発生する。
この座屈が発生する座屈荷重を求めるには、
上で単純梁に対する座屈荷重を求めるのと同じようにして、
境界条件を変えればいいとは思うが、
実は、様々な境界条件で生じる座屈モードは、
単純梁の座屈モードの一部になっている
(あるいは単純梁の座屈モードの方が一部になっている)と
考えることによって、単純梁の座屈公式を流用して座屈荷重を求めることができる。
例えば、図のような長さ$\ell$の片持ち梁の場合、
これは、長さ$L=2\ell$の単純梁の1次の座屈モードのちょうど半分と考えれば、
長さ$L=2\ell$の単純梁の座屈荷重と同じだと考えることができる。
つまり、単純梁のオイラーの座屈公式から、
${\displaystyle
P_{cr}^{長さ\ell の片持ち梁}=
P_{cr}^{長さLの単純梁}
=\left(\frac{n\pi}{L}\right)^{2}EI
=\left(\frac{n\pi}{2\ell}\right)^{2}EI
\;\;\;\;(n=1,2,3,....)}\;\;\;\;\;$
つまり、単純梁と同じ長さの片持ち梁を圧縮した場合、
座屈荷重は単純梁の$\frac{1}{4}$になるから、
単純支持条件よりもかなり座屈しやすくなるということだ。
このように、対象としている梁(今回は片持ち梁)の実際の長さ$\ell$に対して、
その構造物が単純梁の1次モード($\sin$ 1 半波)で座屈している長さ$L$(今回は$2\ell$)
のことを有効座屈長と言う。
また、有効座屈長が、対象としている梁の実際の長さ$\ell$の何倍になっているかを
有効座屈長係数$K$で表す。
今回の片持ち梁の場合は、$K=2$となる。
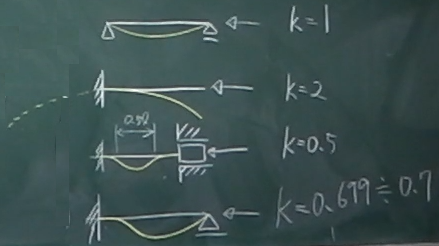 そうすると、有効座屈長は$K\ell$と表されるから、
図のような各種の境界条件に対する座屈荷重は、$K$を用いて以下のように表される。
そうすると、有効座屈長は$K\ell$と表されるから、
図のような各種の境界条件に対する座屈荷重は、$K$を用いて以下のように表される。
${\displaystyle
P_{cr}
=\left(\frac{n\pi}{K\ell}\right)^{2}EI
\;\;\;\;(n=1,2,3,....)}\;\;\;\;\;$
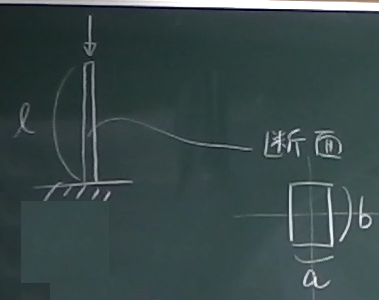 図のような柱の座屈荷重を求めてみよう。
断面は図のような$a\times b$の長方形断面、
ヤング率は$E$とする。
公式から、
図のような柱の座屈荷重を求めてみよう。
断面は図のような$a\times b$の長方形断面、
ヤング率は$E$とする。
公式から、
${\displaystyle
P_{cr}
=\left(\frac{n\pi}{K\ell}\right)^{2}EI
\;\;\;\;(n=1,2,3,....)}\;\;\;\;\;$
となるが、片持ち梁なので、有効座屈長係数は
$K=2$, 柱のオイラー座屈は最低次で生じるので$n=1$となり、
${\displaystyle
P_{cr}
=\frac{\pi^{2}}{4\ell^{2}}EI
}$
あとは、断面2次モーメント$I$を求めればよい。
断面2次モーメントは、長方形断面のどの軸回りの断面2次モーメントを
求めればいいだろうか。
 実際の柱は、最も座屈しやすい方向に座屈するので、
断面2次モーメントが最も小さい軸回りに曲がって座屈する。
つまり、最も断面2次モーメントが小さくなる軸回りの断面2次モーメントを
求めればよい。
長方形断面の場合、短辺の中央を通る軸(図の「弱軸」)回りの
断面2次モーメントが最も小さいから、
この軸回りの断面2次モーメント$I_{弱}$を求めればよい。
ちなみに、$\text{I}$型断面の梁など、2軸対称な部材では、
通常、曲げを受ける断面2次モーメントの大きい方の軸を「強軸」、
その直角方向の断面2次モーメントの小さい方の軸を「弱軸」と言う。
ただ、断面2次モーメントというのは、
部材が使われる際の直角な2軸以外にもあらゆる軸回りの
断面2次モーメントがあり得るので、
例えば$\text{L}$型断面とかでは、
実際の柱は、最も座屈しやすい方向に座屈するので、
断面2次モーメントが最も小さい軸回りに曲がって座屈する。
つまり、最も断面2次モーメントが小さくなる軸回りの断面2次モーメントを
求めればよい。
長方形断面の場合、短辺の中央を通る軸(図の「弱軸」)回りの
断面2次モーメントが最も小さいから、
この軸回りの断面2次モーメント$I_{弱}$を求めればよい。
ちなみに、$\text{I}$型断面の梁など、2軸対称な部材では、
通常、曲げを受ける断面2次モーメントの大きい方の軸を「強軸」、
その直角方向の断面2次モーメントの小さい方の軸を「弱軸」と言う。
ただ、断面2次モーメントというのは、
部材が使われる際の直角な2軸以外にもあらゆる軸回りの
断面2次モーメントがあり得るので、
例えば$\text{L}$型断面とかでは、
![]() みたいな
斜めの軸回りの最も断面2次モーメントが小さい軸回りに座屈する。
みたいな
斜めの軸回りの最も断面2次モーメントが小さい軸回りに座屈する。
第6回でやった
長方形断面の断面2次モーメントの公式から、
この長方形断面の弱軸回りの断面2次モーメントは、
$I_{弱}=\frac{ba^{3}}{12}$となるから、
この柱の座屈荷重は、以下のようになる。
${\displaystyle
P_{cr}
=\frac{\pi^{2}}{4\ell^{2}}EI=\frac{\pi^{2}}{4\ell^{2}}E\cdot
\frac{ba^{3}}{12}
=\frac{\pi^{2}ba^{3}E}{48\ell^{2}}
}$
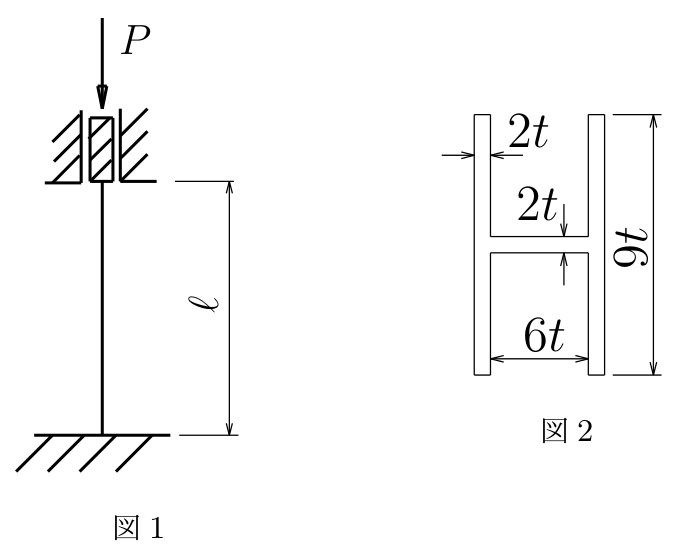 図1のように床面と天井とで両端固定された柱の天井部が、
柱軸に沿って回転を許さずに鉛直方向のみに変位できるようになっている。
この柱の天井部に図1のように鉛直下向き荷重を載荷して座屈させる。
断面は図2のような2軸対称の$\text{H}$型断面である。
有効座屈長$K\ell$, 弱軸回りの断面2次モーメント$I_{弱}$,
座屈荷重$P_{cr}$を求めよ。ただし、材料のヤング率は$E$, 円周率は$\pi$とする。
(2017年度定期試験)
図1のように床面と天井とで両端固定された柱の天井部が、
柱軸に沿って回転を許さずに鉛直方向のみに変位できるようになっている。
この柱の天井部に図1のように鉛直下向き荷重を載荷して座屈させる。
断面は図2のような2軸対称の$\text{H}$型断面である。
有効座屈長$K\ell$, 弱軸回りの断面2次モーメント$I_{弱}$,
座屈荷重$P_{cr}$を求めよ。ただし、材料のヤング率は$E$, 円周率は$\pi$とする。
(2017年度定期試験)
 答えはここ。
計算過程はないが、断面2次モーメントの求め方について、
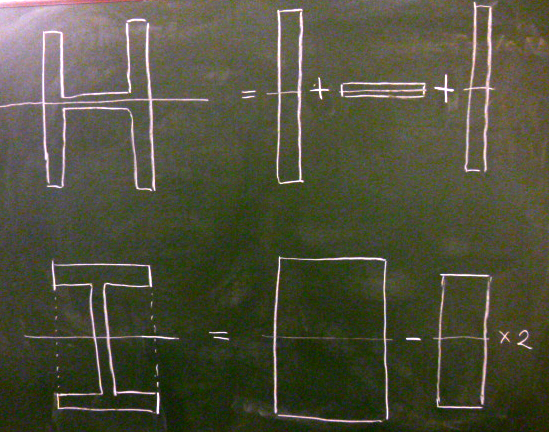
ちょっとヒントを出すと、図のような
$\text{H}$型の図心軸回り断面2次モーメントを求める場合は、
両側の細長い長方形と真ん中の平べったい長方形に分割できるから、
これら3つの長方形の断面2次モーメントを足し算すれば求まる。
答えはここ。
計算過程はないが、断面2次モーメントの求め方について、
ちょっとヒントを出すと、図のような
$\text{H}$型の図心軸回り断面2次モーメントを求める場合は、
両側の細長い長方形と真ん中の平べったい長方形に分割できるから、
これら3つの長方形の断面2次モーメントを足し算すれば求まる。
また、
図のような$\text{I}$型の図心軸回りの断面2次モーメントを求める場合は、
$\text{I}$の上下フランジを結んだ大きい長方形の断面2次モーメントから、
内側のくびれ(空間)をつくっている小さい長方形2個ぶんの断面2次モーメントを
引けば求まる。
もちろん、第6回でやったように、面積積分してもいいし、
図心軸から離れた軸回りの公式を利用してもよい。
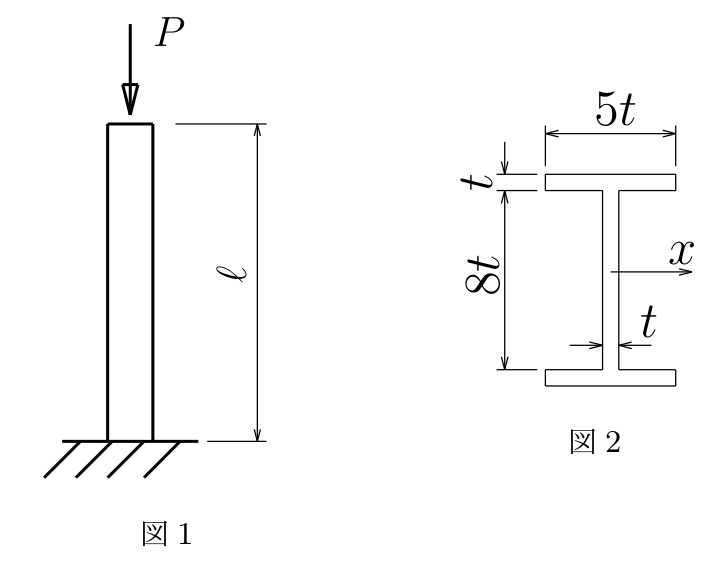 床面で完全固定された鉛直な柱の上側の自由端に、
図1のように鉛直下向き荷重を載荷して座屈させる。
断面は図2のような2軸対称の$\text{I}$型断面である。
有効座屈長$K\ell$, 弱軸回りの断面2次モーメント$I_{弱}$,
座屈荷重$P_{cr}$を求めよ。ただし、材料のヤング率は$E$である。
(2016年度定期試験)
床面で完全固定された鉛直な柱の上側の自由端に、
図1のように鉛直下向き荷重を載荷して座屈させる。
断面は図2のような2軸対称の$\text{I}$型断面である。
有効座屈長$K\ell$, 弱軸回りの断面2次モーメント$I_{弱}$,
座屈荷重$P_{cr}$を求めよ。ただし、材料のヤング率は$E$である。
(2016年度定期試験)
答えはここ。
計算過程はありません。
2021年度小テスト:
問,
解答
2020年度小テスト:
問,
解答
メモ: