以下の話の流れや導出方法等は、 後藤の恩師の岩熊先生と後輩の小山さんとの共著： 岩熊哲夫・小山茂『鬆徒労苦衷有迷禍荷苦痛-- 計算機による構造解析の基礎としての構造力学を独習する』 の 10. 振動論の基礎 のやり方を参考にしています。 まだ、準備開始したばかりなので、間違いとか、それなりにあるかもしれません。 大幅に書き換える可能性もあります。
オイラーの公式：
$e^{ix}=\cos x+i\sin x$
$e^{-ix}=\cos x-i\sin x$
加法定理：
$\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta$
$\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta$
三角関数の合成(加法定理の逆)：
$a\sin\theta-b\cos\theta=\sqrt{a^{2}+b^{2}}
\left(
\frac{a}{\sqrt{a^{2}+b^{2}}}\sin\theta
-\frac{b}{\sqrt{a^{2}+b^{2}}}\cos\theta
\right)\\
=\sqrt{a^{2}+b^{2}}(\sin\theta\cos\alpha-\cos\theta\sin\alpha)\\
=\sqrt{a^{2}+b^{2}}\sin(\theta-\alpha)$
だたし、
$\cos\alpha=\frac{a}{\sqrt{a^{2}+b^{2}}}\;$,
$\sin\alpha=\frac{b}{\sqrt{a^{2}+b^{2}}}$.
つまり、$\tan\alpha=\frac{b}{a}$
部分積分：
${\displaystyle \int_{a}^{b}f(x)g'(x)dx
=\left[f(x)g(x)\right]_{a}^{b}-\int_{a}^{b}f'(x)g(x)dx}$
$\omega=\sqrt{\frac{k}{m}}$
$\beta=\frac{c}{2m\omega}$
$\omega_{d}=\omega\sqrt{1-\beta^{2}}$
ばね定数$k$のばねに質量$m$の質点をくっつけて、
静かに離したら、つりあって静止したとする。
このとき、自然長のばねの先端を原点とすると、
ばねの静的つりあい位置までの下向き変位はフックの法則から$\frac{mg}{k}$となる。
さて、この質点に外力$f(t)$を作用させて振動させたとする。
このときの質点の下向き変位を、図のように
自然長のばねの先端を原点とした場合は$y(t)$と表し、
静的つりあい状態のときのばねの先端を原点とした場合は$v(t)$と表すことにする。
すると、$y(t)=v(t)+\frac{mg}{k}$の関係がある。
このとき、質点をばねから切り離して、質点についての運動方程式を
考える。
ニュートンの法則は、下向きの力の合計が
質量かける下向きの加速度と書けるだろうから、
$\sum\downarrow = m\ddot{y}$
みたいに書けるだろう。ちなみに、上ドットは時間$t$についての微分なので、
$\ddot{y}=\frac{d^{2}y}{dt^{2}}$ということ。
左辺に下向きの力の合計を書くと、
$f(t)+mg-ky(t)=m\ddot{y}(t)$
となる。
ちなみに、加速度運動する質点と一緒に運動している人から見ると、
質点は静止していて、上向きに$m\ddot{y}$つまり下向きに$-m\ddot{y}$の
見かけ上の力(いわゆる慣性力)が作用してつりあっているようにも
見えるから、そのように解釈するなら、
$\sum_{質点}\downarrow =f(t)+mg-ky(t)-m\ddot{y}(t)=0$
と考えてもいい。
私は全体座標系(この場合、慣性の法則が成り立つ慣性系)で
ニュートンの法則(質点に作用する下向きの力の合計=
質点の質量$\times$下向きの加速度)と捉えた方が混乱しないので、
今後はこっちの考え方で運動方程式をたてていく。
さて、$y(t)=v(t)+\frac{mg}{k}$だったから、
$\ddot{y}(t)=\ddot{v}(t)$なので、
上の運動方程式に、$y(t)=v(t)+\frac{mg}{k}$と$\ddot{y}(t)=\ddot{v}(t)$を
代入すると、
$m\ddot{v}(t)+kv(t)=f(t)$
と書ける。
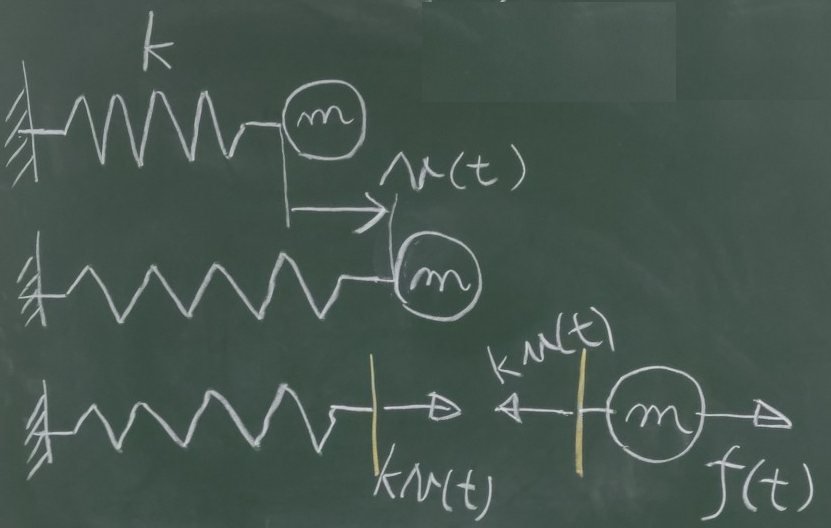ちなみに、これは重力が入らないようにばねを横に向けて、
静的つりあい位置からの変位を$v(t)$として振動させた場合の運動方程式と同じである。
$-kv(t)+f(t)=m\ddot{v}(t)$
高校の教科書だと、$-kx$の復元力が働くから$ma=-kx$みたいな説明だったりして、
私は、どうしてマイナスがつくのか、なかなか理解できなかったが、
構造力学の捉え方で、
引張を正とした内力(軸力)が(質点側の切断面では左向きに)作用していると考えれば(私は)すっきりする。
まず、減衰のない自由振動を考える。
質点をひっぱって離したら振動を始めたとか、そういう状態。
振動の最中に外力を加えてはいないので$f(t)=0$で、
$m\ddot{v}(t)+kv(t)=0$
となる。
$v(t)$についての微分方程式を解きやすくするため、
$\omega=\sqrt{\frac{k}{m}}$とおくと、
$\ddot{v}(t)+\omega^{2}v(t)=0$
と書ける。
さて、こんな形($v''+\alpha^{2}v=0$)の微分方程式は、
座屈の問題とかよく出てくるけど、
$v(t)=e^{\lambda t}$とおくと、
$\dot{v}(t)=\lambda e^{\lambda t}$
$\ddot{v}(t)=\lambda^{2}e^{\lambda t}$
だから、これらを
$\ddot{v}(t)+\omega^{2}v(t)=0$
に代入すると
$(\lambda^{2}+\omega^{2})e^{\lambda t}=0$
これがすべての$t$に成り立つから、
$\lambda^{2}+\omega^{2}=0$
これは特性方程式というやつだ。
この解は$\lambda=\pm\omega i$となり、
一般解は、独立な解$e^{i\omega t}$, $\;e^{-i\omega t}$の線形結合
ということで
$v(t)=C_{1}e^{i\omega t}+C_{2}e^{-i\omega t}$
となる。$C_{1}, \;C_{2}$は任意の定数(複素数)。
オイラーの公式から
$e^{i\omega t}=\cos\omega t+i\sin\omega t$
$e^{-i\omega t}=\cos\omega t-i\sin\omega t$
だから、これらを代入すると、
$v(t)=(C_{1}+C_{2})\cos\omega t+(C_{1}-C_{2})i\sin\omega t$
みたいになる。
$v(t)$は変位だから実数なのに、$i$が入っているのは気持ち悪いので、
任意の実数定数$A,B$を使って、
$C_{1}=\frac{B-iA}{2}$, $\;C_{2}=\frac{B+iA}{2}$とおいて代入すると、
$v(t)=A\sin\omega t+B\cos\omega t$
となり、$i$が消える。$A, B$は任意の実数定数で初期条件から求まる。
(このような物理の問題に出てくる微分方程式の解法は、
金沢工業大学のKIT物理ナビゲーションで
丁寧に解説している。)
例えば、$t=0$のとき、$v(0)=v_{0}$の位置まで質点を引っ張って
静かに離したんだとすると、
$v(0)=B=v_{0}$となる。
また、$t=0$での質点の速度が0であることから$A$を求めるため、$v(t)$の
1階微分を求めると、
$\dot{v}(t)=\omega A\cos\omega t-\omega B\sin\omega t$
となるので、
$\dot{v}(0)=\omega A=0$から$A=0$となり、
$v(t)=v_{0}\cos\omega t$
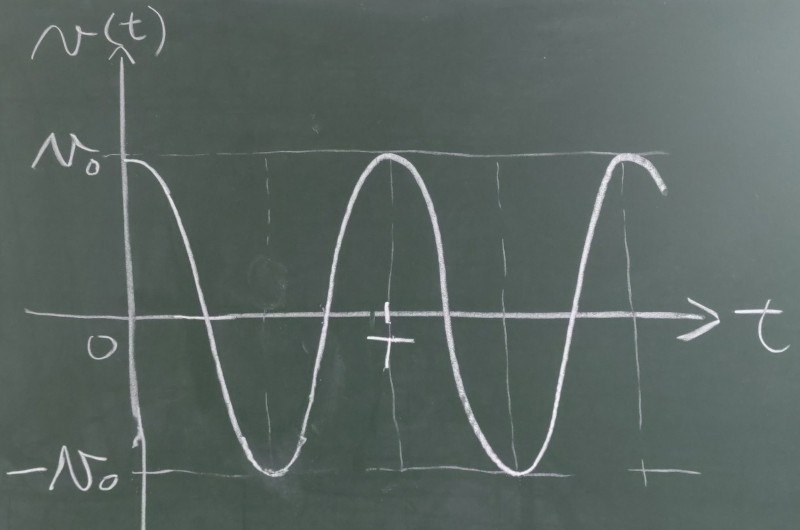となる。
この場合、振幅は$v_{0}$で、周期$T$は$T=\frac{2\pi}{\omega}$となる。
これの逆数$\frac{\omega}{2\pi}$は固有振動数である。
これに$2\pi$をかけて単位をradで表した$\omega$は、
固有角振動数である。
(自由振動しか扱わない)高校の教科書等では、特に「固有」とつけずに振動数と言うと思うが、
構造物の振動を扱うような場合は、
自由振動させたときの振動数は(共振する振動数という意味でも)
強制振動等の振動数とは区別して固有振動数と言う。
弦楽器の弦の振動とか、音声の場合も、
同じ長さの弦だったら、
いつもその音が出るという
意味で「固有」とつけることが多いかもしれない。
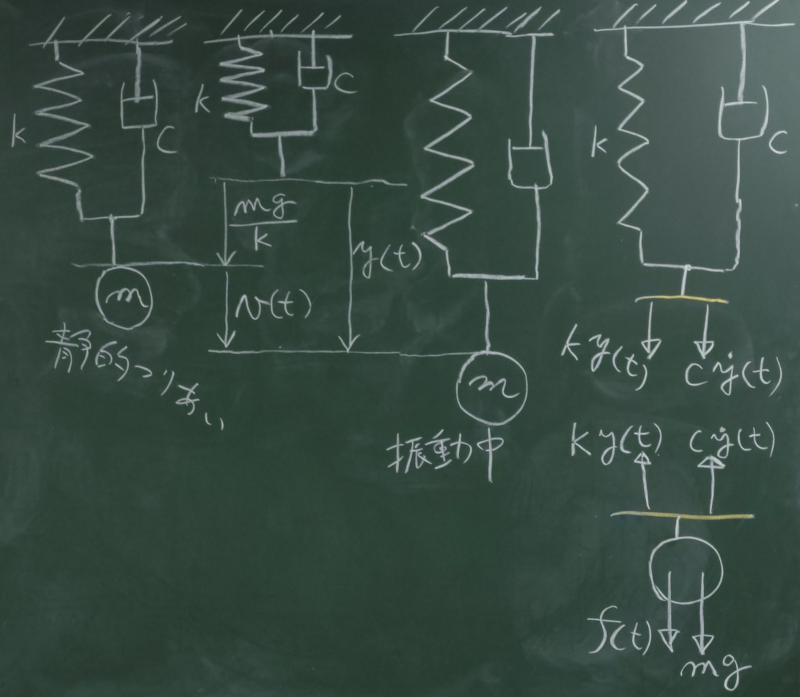実際に自由振動する振動系は、空気抵抗や摩擦など、様々な原因で減衰していく。
ここでは、減衰の代表的なモデルとして、速度に比例した粘性減衰について考える
(その他のモデルについては、
この辺参照)。
図のように、ばね定数$k$のばねと並列に
粘性減衰係数$c$のダッシュポッドが取り付けられた振動系を考える。
ダッシュポッドというのは、液体の入った注射器みたいな装置で、
両端を持って軸方向に押したり引っ張ったりすると、
中の液体がピストンの脇から(あるいはピストンに設けた穴から)移動して、
ゆっくり動く。
その際、動かす速度に比例する抵抗力が生じ、その比例定数$c$を
粘性減衰係数と呼ぶ。
減衰なしの場合と同様の座標や表記で、
振動中の質点を切り離して、質点についての運動方程式を考えると、
質点に作用する力は、
減衰なしのときに加えて(引張を正として)
上向きの$c\dot{y}(t)$を
考慮すればいいだけだから、
$f(t)+mg-ky(t)-c\dot{y}(t)=m\ddot{y}(t)$
となる。
さて、
上の運動方程式に、$y(t)=v(t)+\frac{mg}{k}$と$\ddot{y}(t)=\ddot{v}(t)$と
$\dot{y}(t)=\dot{v}(t)$を
代入すると、
$m\ddot{v}(t)+c\dot{v}(t)+kv(t)=f(t)$
と書ける。
減衰なしのときと同じような形式に書けるように、
$\omega=\sqrt{\frac{k}{m}}, \;\;\;\;\;
\beta=\frac{c}{2m\omega}$
とおくと、
$\ddot{v}(t)+2\beta\omega\dot{v}(t)+\omega^{2}v(t)=\frac{f(t)}{m}$
と書ける。
以下では、外力$f(t)$がない減衰自由振動の場合を考えると、
$\ddot{v}(t)+2\beta\omega\dot{v}(t)+\omega^{2}v(t)=0$
と書ける。
この$\beta$は減衰定数と呼ばれる。
さて、1階微分の項$\dot{v}(t)$を含むと、
2階の微分方程式の一般解を求めるのは途端に難しくなる。
$v(t)=e^{\lambda t}$とおいて代入すると、
$\dot{v}(t)=\lambda e^{\lambda t}$,
$\ddot{v}(t)=\lambda^{2}e^{\lambda t}$だから、
$\lambda^{2}+2\beta\omega\lambda+\omega^{2}=0$
となる。これを特性方程式というが、
これを満たす$\lambda$のときの$v(t)=e^{\lambda t}$が
解にになるのだが、
解の公式で特性方程式の解を求めると、
$\lambda=\omega(-\beta\pm\sqrt{\beta^{2}-1})$
となる。
すると、$\beta<1$かどうかで、
$\sqrt{\beta^{2}-1}$が虚数になるかどうかが変わるので、
$\beta$の大きさによって、解の性質が変わってくる。
ちゃんと一般解を求めたいときは、以下のサイトなどを参照してもらうとして、
７．粘性減衰力がある場合の１自由度系の自由振動(山口大学 齊藤 俊先生)
減衰振動 ： 微分方程式の解法 (金沢工業大学 KIT物理ナビゲーション)
土木構造物の場合、$\beta\ll 1$(例えば、0.05とかそういう値)で
$\sqrt{\beta^{2}-1}$が虚数になるのが確実で
あることから、
特性方程式の解を、
$\lambda =\omega(-\beta\pm\sqrt{-1\cdot (1-\beta^{2})}
=-\beta\omega\pm i\omega_{d}$
ただし、$\omega_{d}=\omega\sqrt{1-\beta^{2}}$とおく。
上の非減衰自由振動のときと同様に、
このときの一般解は、
独立な解
$e^{(-\beta\omega+i\omega_{d})t}$,
$\;e^{(-\beta\omega-i\omega_{d})t}$の線形結合だから、
$v(t)=C_{1}e^{-\beta\omega t+i\omega_{d}t}+C_{2}e^{-\beta\omega t-i\omega_{d}t}$
$=e^{-\beta\omega t}
\left(
C_{1}e^{i\omega_{d}t}+C_{2}e^{-i\omega_{d}t}\right)$
となる。$C_{1}, \;C_{2}$は任意の定数(複素数)。
オイラーの公式から
$e^{i\omega_{d} t}=\cos\omega_{d} t+i\sin\omega_{d} t$
$e^{-i\omega_{d} t}=\cos\omega_{d} t-i\sin\omega_{d} t$
だから、これらを代入すると、
$v(t)=e^{-\beta\omega t}
\left(
(C_{1}+C_{2})\cos\omega_{d} t+(C_{1}-C_{2})i\sin\omega_{d} t
\right)
$
となる。
$v(t)$は変位だから実数なのに、$i$が入っているのは気持ち悪いので、
任意の実数定数$A,B$を使って、
$C_{1}=\frac{B-iA}{2}$, $\;C_{2}=\frac{B+iA}{2}$とおいて代入すると、
$v(t)=e^{-\beta\omega t}
\left(
A\sin\omega_{d} t+B\cos\omega_{d} t
\right)
$
となり、$i$が消える。$A, B$は任意の実数定数で初期条件から求まる。
(このような振動の問題に出てくる微分方程式の解法は、
金沢工業大学のKIT物理ナビゲーションで
丁寧に解説している。)
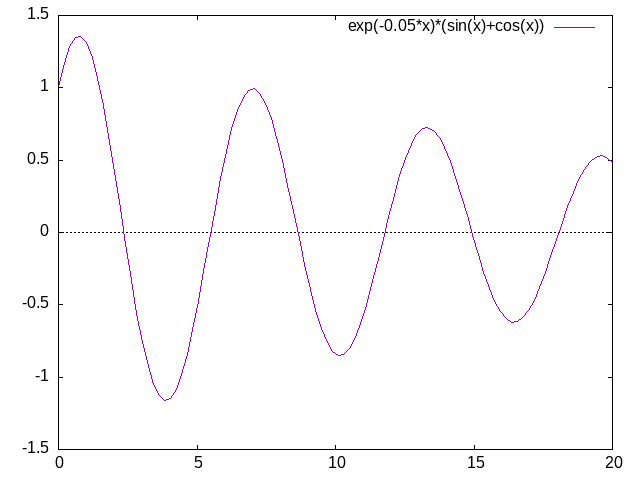この場合の周期$T$は、
$T=\frac{2\pi}{\omega_{d}}=\frac{2\pi}{\omega\sqrt{1-\beta^{2}}}\simeq\frac{2\pi}{\omega}$
となる。土木構造物では、$\beta$は$0.02\sim 0.05$以下とか非常に小さいから、
$\omega_{d}\simeq \omega$である。
さて、
$v(t)=e^{-\beta\omega t}(A\sin\omega_{d}t+B\cos\omega_{d}t)$
において、$\sin\alpha=-\frac{A}{C}, \;\cos\alpha=\frac{B}{C}$とおいて変形すると、
$v(t)=e^{-\beta\omega t}(A\sin\omega_{d}t+B\cos\omega_{d}t)$
$=Ce^{-\beta\omega t}(\frac{B}{C}\cos\omega_{d}t+\frac{A}{C}\sin\omega_{d}t)$
$=Ce^{-\beta\omega t}(\cos\omega_{d}t\cos\alpha-\sin\omega_{d}t\sin\alpha)$ ここで加法定理を用いると
$v(t)=Ce^{-\beta\omega t}\cos(\omega_{d}t+\alpha)$
のように表せる。$C, \alpha$は任意の定数。
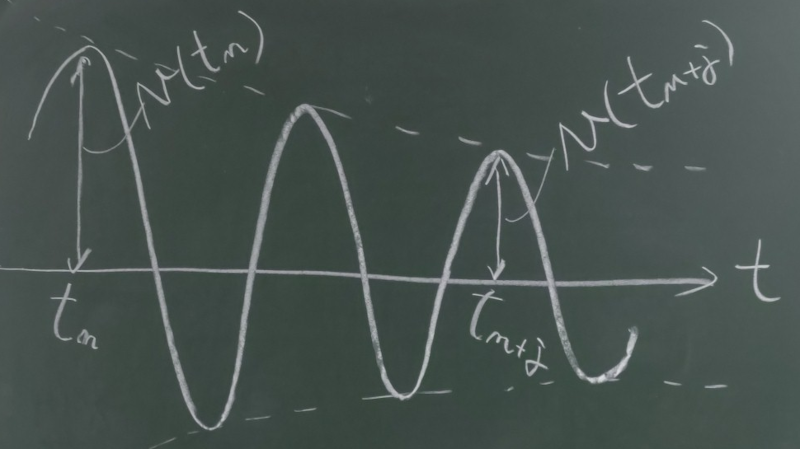
図のような、減衰曲線の$n$番目の正のピーク値が、
$t=t_{n}$のときに現れるとすると、
$n+j$番目のピークは、
そこから周期$T=\frac{2\pi}{\omega_{d}}$が$j$個ぶんだけずれた
ところにあらわれるから、
$t_{n+j}=t_{n}+jT=t_{n}+\frac{2\pi}{\omega_{d}}j$となる。
このとき、$n$番目のピークと$n+j$番目のピークの比を
減衰比と呼び、以下のように表される。
$\frac{v(t_{n})}{v(t_{n+j})}=
\frac{Ce^{-\beta\omega t_{n}}\cos(\omega_{d}t_{n}+\alpha)}
{Ce^{-\beta\omega t_{n+j}}\cos(\omega_{d}t_{n}+2\pi j+\alpha)}\\
=\frac{e^{-\beta\omega t_{n}}}{e^{-\beta\omega t_{n+j}}}
=\frac{e^{-\beta\omega t_{n}}}{e^{-\beta\omega(t_{n}+\frac{2\pi}{\omega_{d}}j)}}
=\frac{e^{-\beta\omega t_{n}}}{e^{-\beta\omega t_{n}}\;e^{-\beta\omega\frac{2\pi}{\omega_{d}}j}
}
=e^{2\pi j\beta\frac{\omega}{\omega_{d}}}
$
つまり、
$\frac{v(t_{n})}{v(t_{n+j})}
=e^{2\pi j\beta\frac{\omega}{\omega_{d}}}
=e^{\frac{2\pi j\beta}{\sqrt{1-\beta^{2}}}} $
となる。この減衰比の自然対数をとったものをを対数減数率と呼ぶが、
以下の$\delta$で与えられる。
$\delta=\ln\frac{v(t_{n})}{v(t_{n+j})}
=\frac{2\pi j\beta}{\sqrt{1-\beta^{2}}}
$
土木構造物では、$\beta\ll 1$なので、
$\delta\simeq 2\pi j\beta$となり、減衰定数は、
減衰曲線のグラフから、
$v(t_{n})$と$v(t_{n+j})$の長さを測って
$\delta=\ln\frac{v(t_{n})}{v(t_{n+j})}$を計算し、
$\beta\simeq \frac{\delta}{2\pi j}$
で求められる。
さて、ここまで簡単のため外力$f(t)$がない問題を扱ってきたが、
$f(t)$を無視する前の減衰を考慮した運動方程式は、
以下のように書けた。
$m\ddot{v}(t)+c\dot{v}(t)+kv(t)=f(t)$
固有角振動数$\omega$や減衰定数$\beta$が見えるように
$\omega=\sqrt{\frac{k}{m}}, \;\;\;\;\;
\beta=\frac{c}{2m\omega}$
とおくと、
$\ddot{v}(t)+2\beta\omega\dot{v}(t)+\omega^{2}v(t)=\frac{f(t)}{m}$
と書けた。
ここでは、典型的な外力の例として$f(t)=f_{0}\sin pt$のような
角振動数$p$の正弦波外力の
場合を考えてみると、運動方程式は、以下のように書ける。
$\ddot{v}(t)+2\beta\omega\dot{v}(t)+\omega^{2}v(t)=\frac{f_{0}}{m}\sin pt$
この一般解は、
斉次解(または同次解。$v$, $\dot{v}$, $\ddot{v}$, $t$等の次数が同じで、
この場合は
$f(t)=0$のときの解)と特殊解(初期条件等から定数を決定した解)との和になるので、
特殊解を(後述するように定常振動に対応するから)$v_{定}(t)$とすると、
$v(t)=e^{-\beta\omega t}(A\sin\omega_{d}t+B\cos\omega_{d}t)+v_{定}(t)$
のように書ける。
斉次解つまりこの場合は減衰自由振動の解
$e^{-\beta\omega t}(A\sin\omega_{d}t+B\cos\omega_{d}t)$
の部分は時間とともに減衰していくので、
十分に時間が経過して定常状態になった後のことを考えるのであれば、
特殊解の方が支配的になる。
なので、
ここでは定常振動に対応する特殊解の方を
ここの
やり方で求めてみる。
特殊解は定常状態に達した振動だと思われるので、
角振動数は強制振動の角振動数$p$と同じになると想定し、
$v_{定}(t)=C\sin pt+D\cos pt$
とおけると仮定する。$C, D$は任意の定数。すると、
$\dot{v}_{定}(t)=pC\cos pt-pD\sin pt$
$\ddot{v}_{定}(t)=-p^{2}C\sin pt-p^{2}D\cos pt$
これらを運動方程式に代入すると、
$-p^{2}C\sin pt-p^{2}D\cos pt
+2\beta\omega pC\cos pt-2\beta\omega pD\sin pt
+\omega^{2}C\sin pt+\omega^{2}D\cos pt
=\frac{f_{0}}{m}\sin pt$
$\sin pt, \cos pt$ごとにまとめると、
$(\sin pt)(-p^{2}C
-2\beta\omega pD
+\omega^{2}C
-\frac{f_{0}}{m})
+(\cos pt)
(-p^{2}D
+2\beta\omega pC
+\omega^{2}D)=0$
となる。
この式が常になりたつには、
$\sin pt$と$\cos pt$にかけてある$()$の中がともに0になればいいから、
$
\left(
\begin{array}{cc}
\omega^{2}-p^{2} & -2\beta\omega p \\
2\beta\omega p & \omega^{2}-p^{2}
\end{array}
\right)
\left(
\begin{array}{c}
C\\
D
\end{array}
\right)
=
\left(
\begin{array}{c}
\frac{f_{0}}{m}\\
0
\end{array}
\right)
$
がなりたてばよい。逆行列をとって$C, D$を求めると、
$
\left(
\begin{array}{c}
C\\
D
\end{array}
\right)
=
\frac{\frac{f_{0}}{k}}
{\left(1-\left(\frac{p}{\omega}\right)^{2}\right)^{2}
+4\beta^{2}\left(\frac{p}{\omega}\right)^{2}}
\left(
\begin{array}{c}
1-\left(\frac{p}{\omega}\right)^{2}\\
-2\beta\frac{p}{\omega}
\end{array}
\right)
$
この$C, D$を$v_{定}(t)$に代入すると、
$v_{定}(t)
=
\frac{\frac{f_{0}}{k}}
{\left(1-\left(\frac{p}{\omega}\right)^{2}\right)^{2}
+4\beta^{2}\left(\frac{p}{\omega}\right)^{2}}
\left(
\left(1-\left(\frac{p}{\omega}\right)^{2}\right)
\sin pt-2\beta\frac{p}{\omega}\cos pt
\right)
$
この式を変形するために、
ちょっと、ここで三角関数の合成(加法定理の逆)の式を確認しておく。
$a\sin\theta-b\cos\theta=\sqrt{a^{2}+b^{2}}
\left(
\frac{a}{\sqrt{a^{2}+b^{2}}}\sin\theta
-\frac{b}{\sqrt{a^{2}+b^{2}}}\cos\theta
\right)\\
=\sqrt{a^{2}+b^{2}}(\sin\theta\cos\alpha-\cos\theta\sin\alpha)\\
=\sqrt{a^{2}+b^{2}}\sin(\theta-\alpha)$
だたし、
$\cos\alpha=\frac{a}{\sqrt{a^{2}+b^{2}}}\;$,
$\sin\alpha=\frac{b}{\sqrt{a^{2}+b^{2}}}$.
つまり、$\tan\alpha=\frac{b}{a}$
では、ここで、$v_{定}(t)$の式において、
$a=1-\left(\frac{p}{\omega}\right)^{2}\;$,
$b=2\beta\frac{p}{\omega}$
とおいて、三角関数の合成を適用してみる。
$v_{定}(t)
=
\frac{\frac{f_{0}}{k}}{a^{2}+b^{2}}
(a\sin pt-b\cos pt)\\
=
\frac{\frac{f_{0}}{k}}{a^{2}+b^{2}}
\sqrt{a^{2}+b^{2}}\sin(pt-\alpha)\\
=
\frac{\frac{f_{0}}{k}}
{\sqrt{a^{2}+b^{2}}}\sin(pt-\alpha)\\
$
ここで、
$a=1-\left(\frac{p}{\omega}\right)^{2}\;$,
$b=2\beta\frac{p}{\omega}$に戻してやると、
${\displaystyle v_{定}(t)
=
\frac{\frac{f_{0}}{k}}
{\sqrt{{\left(1-\left(\frac{p}{\omega}\right)^{2}\right)^{2}
+4\beta^{2}\left(\frac{p}{\omega}\right)^{2}}}}
\sin(pt-\alpha)
}$
ただし、
${\displaystyle \tan\alpha=\frac{2\beta\frac{p}{\omega}}{1-\left(\frac{p}{\omega}\right)^{2}}}$
となる。
ここで、外力の最大値$f_{0}$が静的に載荷されたときの変位を
静的最大変位$v_{静}=\frac{f_{0}}{k}$で表して、
${\displaystyle M_{D}=
\frac{1}
{
\sqrt{{\left(1-\left(\frac{p}{\omega}\right)^{2}\right)^{2}
+4\beta^{2}\left(\frac{p}{\omega}\right)^{2}}}
}}$
とおくと、
$v_{定}(t)=v_{静}M_{D}\sin(pt-\alpha)$
と書ける。
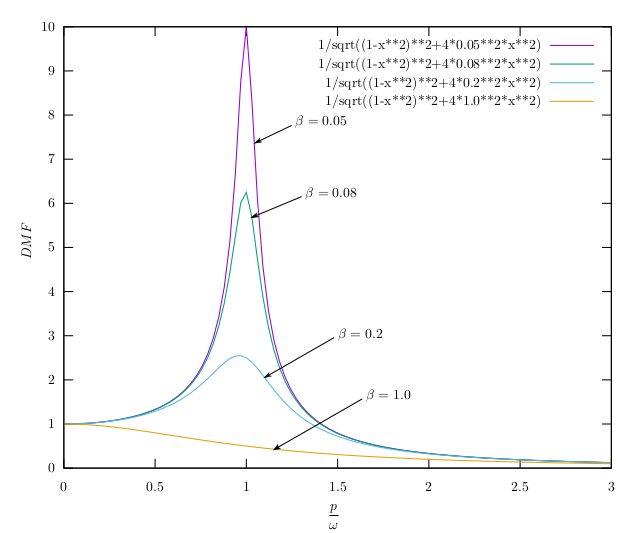この$M_{D}$は動的増幅率(Dynamic Magnification Factor)とかDMFとか呼ばれるのだが、
動的変位を静的変位で割ったもの
（強制外力が$f_{0}\sin pt$のこの例の場合だと、
$M_{D}\sin(pt-\alpha)$のこと)を
DAF(Dynamic Amplification Factor)とか、日本語ではこちらも動的増幅率と
呼んだりするので、ここでは、DMFの方は$M_{D}$と表記しておく。
$DAF=\frac{v(t)}{v_{静}}$で定義されるDAFについては、
また後で触れる。
$DAF$は橋梁のケーブルが切れたりした場合の
ステップ荷重のような外力を受ける場合に
よく出てくるが、
正弦波外力みたいな問題では、あまり使われないのではないかと思う。たぶん。
強制外力の角振動数$p$が、固有角振動数$\omega$に近づけば、
$M_{D}$はどんどん大きくなり、
$p=\omega$のとき、
$M_{D}=\frac{1}{2\beta}$となる。
この状態を共振と呼ぶ。
$\beta$が0であれば、$M_{D}$は無限大となる。
橋梁では$\beta$は非常に小さいので、共振が
起きないように注意する必要がある。
1自由度系の質点に、時刻$t=\tau$で
「大きさ」が1の単位衝撃外力$f(t)$が作用したとする。
衝撃というのは、$t=\tau$の一瞬に作用するというよりは、
非常に短い時間(例えば$\Delta t$)の間に作用する外力と捉えた方が
現実に近いので、
時刻$t=\tau-\frac{\Delta t}{2}$
から
時刻$t=\tau+\frac{\Delta t}{2}$
までの間に$f(t)$が作用するモデルを考える。
$f(t)$の大きさが1というのは、これを$\Delta t$の区間で
積分して合計したものが1ということで、
${\displaystyle \int_{\tau-\frac{\Delta t}{2}}^{\tau+\frac{\Delta t}{2}}
f(t)dt=1}$
のように表せるだろう。
ただし、大きさは1ではあるが、次元は力$\times$時間で、力積の次元になっている。
以降、1などの定数項が出てきても、次元は定数項でない項を見て判断してほしい。
$f(t)$が作用している間の運動方程式は、
$m\ddot{v}(t)+c\dot{v}(t)+kv(t)=f(t)$
となるが、
これの両辺を
$\tau-\frac{\Delta t}{2}$から$\tau+\frac{\Delta t}{2}$まで
積分してみる。右辺の積分は1だが、左辺は色々あるので、
まずは慣性項$m\ddot{v}(t)$から。
${\displaystyle
\int_{\tau-\frac{\Delta t}{2}}^{\tau+\frac{\Delta t}{2}}
m\ddot{v}(t)dt=
[
m\dot{v}(t)
]
_{\tau-\frac{\Delta t}{2}}^{\tau+\frac{\Delta t}{2}}
=
m\dot{v}(\tau+\frac{\Delta t}{2})-
m\dot{v}(\tau-\frac{\Delta t}{2})
}$
これは、運動量の変化だ。
次に粘性項$c\dot{v}(t)$。
${\displaystyle
\int_{\tau-\frac{\Delta t}{2}}^{\tau+\frac{\Delta t}{2}}
c\dot{v}(t)dt=
[
cv(t)
]
_{\tau-\frac{\Delta t}{2}}^{\tau+\frac{\Delta t}{2}}
=
cv(\tau+\frac{\Delta t}{2})-
cv(\tau-\frac{\Delta t}{2})
}$
$v(t)$は
静的つりあい位置を原点$0$とする変位なので、
衝撃を受けた瞬間は
ほとんど$0$で、
$v(\tau-\frac{\Delta t}{2})\simeq 0$,
$v(\tau+\frac{\Delta t}{2})\simeq 0$
と見なせるとするなら、
$cv(t)\simeq 0$となる。
次に剛性項$kv(t)$の積分
${\displaystyle
\int_{\tau-\frac{\Delta t}{2}}^{\tau+\frac{\Delta t}{2}}
kv(t)dt}$
だが、これも同様に、
$v(t)$は
衝撃を受けた瞬間は
ほとんど$0$で、
$v(\tau-\frac{\Delta t}{2})\simeq 0$,
$v(\tau+\frac{\Delta t}{2})\simeq 0$
と見なせるとするなら、
横軸$t$, 縦軸$v(t)$のグラフで、この定積分を表す領域の面積は
ほぼ$0$になるので、
${\displaystyle
\int_{\tau-\frac{\Delta t}{2}}^{\tau+\frac{\Delta t}{2}}
kv(t)dt}\simeq 0$
以上より、
${\displaystyle
\int_{\tau-\frac{\Delta t}{2}}^{\tau+\frac{\Delta t}{2}}
(m\ddot{v}(t)+c\dot{v}(t)+kv(t))dt
=
\int_{\tau-\frac{\Delta t}{2}}^{\tau+\frac{\Delta t}{2}}
f(t) dt
}
$
の左辺の積分を実行した結果は、以下のようになる。
${\displaystyle
m\dot{v}(\tau+\frac{\Delta t}{2})-
m\dot{v}(\tau-\frac{\Delta t}{2})
=
\int_{\tau-\frac{\Delta t}{2}}^{\tau+\frac{\Delta t}{2}}
f(t) dt
}$
この式の左辺は
時刻$t=\tau-\frac{\Delta t}{2}$
から
時刻$t=\tau+\frac{\Delta t}{2}$
までの
運動量の変化で、
右辺はその間の力積だから、
この式は質点の運動量の変化はその間に質点が受けた力積に等しい
ことを表している。
さて、$f(t)$は単位衝撃外力で、
${\displaystyle \int_{\tau-\frac{\Delta t}{2}}^{\tau+\frac{\Delta t}{2}}
f(t)dt=1}$なので、
${\displaystyle
m\dot{v}(\tau+\frac{\Delta t}{2})-
m\dot{v}(\tau-\frac{\Delta t}{2})
=1}$
ちょっと詭弁っぽいかもしれないが、
$t=\tau$に衝撃を受けるまでは質点は静止していて、
衝撃を受けた途端に動き出したとすると、
$t\lt \tau$では$\dot{v}(t)=0$になるから、
$m\dot{v}(\tau-\frac{\Delta t}{2})=0$となり
${\displaystyle
\dot{v}(\tau+\frac{\Delta t}{2})
=\frac{1}{m}}$
これまた詭弁っぽいが、衝撃を受け(て動き出し)た瞬間の質点の速度$\dot{v}(\tau)$は、
$\Delta t$が非常に小さいと考えれば、
${\displaystyle
\dot{v}(\tau)
=\frac{1}{m}}$
としてよさそうだ。
そうすると、時刻$t=\tau$に単位衝撃外力$f(t)$が作用した質点が
動き出す$t\gt\tau$における運動方程式は、
$m\ddot{v}(t)+c\dot{v}(t)+kv(t)dt=0$
となり、$t=\tau$における初期条件は、
$v(\tau)=0, \;\dot{v}(\tau)=\dfrac{1}{m}$
で与えられる。
この運動方程式は上の減衰自由振動の運動方程式だから、
一般解は、
$v(t)=e^{-\beta\omega t}(A\sin\omega_{d}t+B\cos\omega_{d}t)$
となる。$A, B$は任意の実数定数。
なお、$t\lt\tau$では $v(t)=0$ である。
初期条件を考慮するために$\dot{v}(t)$を求めると
$\dot{v}(t)=-\beta\omega
e^{-\beta\omega t}(A\sin\omega_{d}t+B\cos\omega_{d}t)
+
e^{-\beta\omega t}\omega_{d}(A\cos\omega_{d}t-B\sin\omega_{d}t)\\
=-\beta\omega v(t)+
e^{-\beta\omega t}\omega_{d}(A\cos\omega_{d}t-B\sin\omega_{d}t)\\
$
となる。
これに初期条件の$\dot{v}(\tau)=\dfrac{1}{m}$を適用すると、
$\dot{v}(\tau)
=-\beta\omega v(\tau)+
e^{-\beta\omega \tau}\omega_{d}(A\cos\omega_{d}\tau-B\sin\omega_{d}\tau)
=\dfrac{1}{m}
$
となる。
1項目は、初期条件$v(\tau)=0$から消えるから、
$\dot{v}(\tau)
=
e^{-\beta\omega \tau}\omega_{d}(A\cos\omega_{d}\tau-B\sin\omega_{d}\tau)
=\dfrac{1}{m}$
ちょっと整理すると、
$A\cos\omega_{d}\tau-B\sin\omega_{d}\tau
=\dfrac{e^{\beta\omega \tau}}{m\omega_{d}}$
となる。また、初期条件$v(\tau)=0$から、
$v(\tau)=e^{-\beta\omega \tau}(A\sin\omega_{d}\tau+B\cos\omega_{d}\tau)=0$
つまり、
$A\sin\omega_{d}\tau+B\cos\omega_{d}\tau=0$
となる。$A, B$を含む式が2つできたから、これらを連立させれば$A, B$が求まる。
ちょっとごちゃごちゃしてるので、マトリクスの掛け算で書くと、
$
\left(
\begin{array}{cc}
\cos\omega_{d}\tau & -\sin\omega_{d}\tau\\
\sin\omega_{d}\tau & \cos\omega_{d}\tau
\end{array}
\right)
\left(
\begin{array}{c}
A\\
B
\end{array}
\right)
=
\left(
\begin{array}{c}
\frac{e^{\beta\omega \tau}}{m\omega_{d}}\\
0
\end{array}
\right)
$
となる。
逆行列を両辺に書けると、
$
\left(
\begin{array}{c}
A\\
B
\end{array}
\right)
=
\left(
\begin{array}{cc}
\cos\omega_{d}\tau & \sin\omega_{d}\tau\\
-\sin\omega_{d}\tau & \cos\omega_{d}\tau
\end{array}
\right)
\left(
\begin{array}{c}
\frac{e^{\beta\omega \tau}}{m\omega_{d}}\\
0
\end{array}
\right)
$
つまり、
$A=
\frac{e^{\beta\omega \tau}}{m\omega_{d}}\cos\omega_{d}\tau$,
$\;B=
-\frac{e^{\beta\omega \tau}}{m\omega_{d}}\sin\omega_{d}\tau$,
これらを一般解
$v(t)=e^{-\beta\omega t}(A\sin\omega_{d}t+B\cos\omega_{d}t)$
に代入すると、
$v(t)=
\dfrac{e^{\beta\omega \tau}
e^{-\beta\omega t}
}{m\omega_{d}}
(\sin\omega_{d}t\cos\omega_{d}\tau-\cos\omega_{d}t\sin\omega_{d}\tau)$
加法定理を使うと
$v(t)=
\dfrac{e^{-\beta\omega(t-\tau)}
}{m\omega_{d}}
\sin\omega_{d}(t-\tau)$
となる。
さて、これは$t\gt\tau$での運動方程式を解いた解で、$t\lt\tau$では$v(t)=0$だから、
まとめると
$v(t)=
\begin{cases}
0 & \;\;(t\lt\tau)\\
\dfrac{e^{-\beta\omega(t-\tau)}
}{m\omega_{d}}
\sin\omega_{d}(t-\tau)
& \;\;(t\gt\tau)
\end{cases}
$
となる。これを単位衝撃応答とか
単位インパルス応答と呼ぶ。
さて、こういう場合分けのある式はやや扱いにくいので、
以下で定義されるヘビサイドの階段関数$H(x)$を使って1つの式で表してみる。
$H(x)=
\begin{cases}
0 & \;\;(x\lt 0)\\
1 & \;\;(x\gt 0)
\end{cases}
$
$t\lt\tau$と$t\gt\tau$の場合は、$t-\tau\lt 0$と$t-\tau\gt 0$の場合と
読み替えられるから、
$H(t-\tau)=
\begin{cases}
0 & \;\;(t\lt \tau)\\
1 & \;\;(t\gt \tau)
\end{cases}
$
を使えば、
時刻$t=\tau$に単位衝撃荷重を受けた際の単位衝撃応答$v_{単}(t-\tau)$は、
$v_{単}(t-\tau)=
\dfrac{e^{-\beta\omega(t-\tau)}
}{m\omega_{d}}
H(t-\tau)\sin\omega_{d}(t-\tau)$
と書ける。減衰がなく$\beta=0$であれば、
$\omega_{d}=\omega\sqrt{1-\beta^{2}}$から、
$v_{単}(t-\tau)=
\dfrac{1}{m\omega}
H(t-\tau)\sin\omega(t-\tau)$
と書ける。
時刻$t=\tau$に単位衝撃荷重を受けた際の単位衝撃応答$v_{単}(t-\tau)$がわかれば、
時刻$t=\tau$に力積の無次元化した大きさが$F$となる衝撃外力を受けた際の応答は、
単位衝撃応答を$F$倍して、
$v(t)=Fv_{単}(t-\tau)$
のように与えられるだろう。
「力積の無次元化した大きさ」というのは、
力積を大きさ1の単位の力積で割り算したものという意味。
要は、単位衝撃応答$v_{単}$にそのままかければいいように無次元化したということ。
以下の式の計算では無次元化されているかどうかは、あまり気にしなくてもいいが、
実際に数値を入れて計算する場合には気にしないといけない。
では、
時刻$t=\tau_{1}$に力積の無次元化した大きさが$F_{1}$となる衝撃外力を受け、
時刻$t=\tau_{2}$に力積の無次元化した大きさが$F_{2}$となる衝撃外力を受け、、、、
時刻$t=\tau_{n}$に力積の無次元化した大きさが$F_{n}$となる衝撃外力を受けた際の応答は、
どうなるだろうか。
ありがたいことに、線形の微分方程式では
重ね合わせの原理が成り立つので、
以下のように、$F_{1}, F_{2},...., F_{n}$の応答をすべて足し算すればいいのだ。
${\displaystyle v(t)=\sum_{i=1}^{n}F_{i}v_{単}(t-\tau_{i})\;\;\;\;(i=1,2,...., n)}$
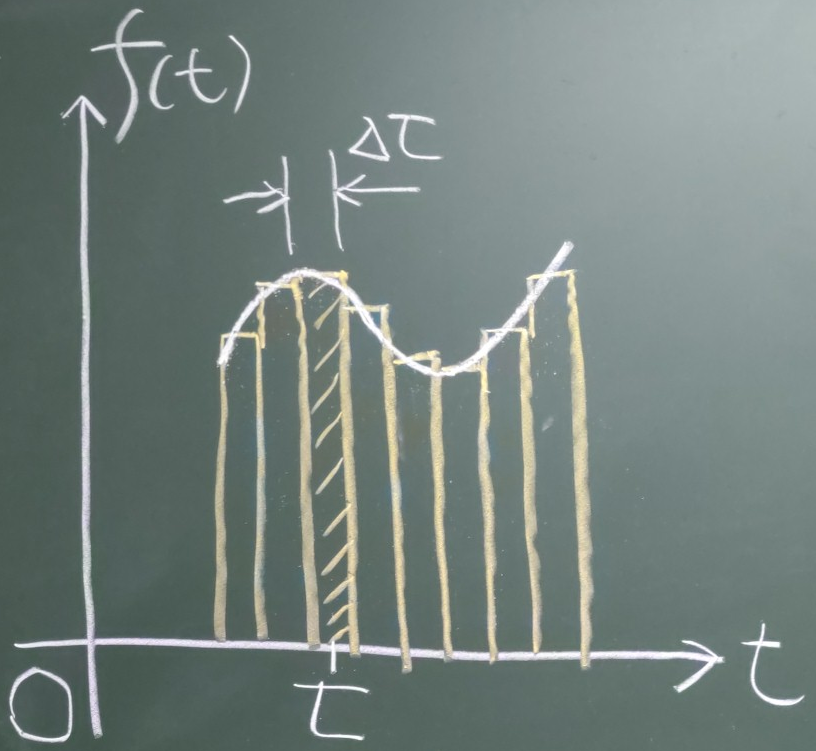では、衝撃外力ではなく、任意の強制外力$f(t)$を受ける場合の応答はどうなるだろうか。
図のように、任意の外力を幅$\Delta\tau$ずつの衝撃荷重に分割して、
$f(\tau)\Delta\tau$を足し算すればいいのではないか。
$\Delta\tau\rightarrow 0$の極限を取ればこの足し算は積分になるから、
時刻$t=0$以降に外力が作用したとして、積分区間を$0$から$\infty$までとすれば、
${\displaystyle v(t)=\int_{0}^{\infty}f(\tau)v_{単}(t-\tau)d\tau}$
と表される。
このように(2つの関数に対して$\int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau$みたいに)
表される積分のことを畳み込み積分とか
デュアメル積分と呼ぶ。
今回の場合、この積分は$t=\tau$に作用した外力$f(\tau)$が全体の応答に及ぼす影響を
表しているが、
信号処理とか様々な分野でよく使われる。
任意外力に対する応答が求められそうになったところで、
ステップ荷重に対する応答を求めてみたい。
ステップ荷重というのは、ある時刻(例えば$t=0$)までは外力が$0$で、
その時刻以降は一定の外力$P$が載荷され続けるような問題である。
ある時刻に吊橋のケーブルが切れ(て外力が抜け)るみたいな外力もステップ荷重で表されると考えられる。
ステップというのは「階段」ということで、さきほどのヘビサイドの階段関数を
ステップ関数と言ったりもする。
だから「階段荷重」と言っても構わないと思うのだが(階段関数とも対応するし)、
検索すると上り降りする階段が受ける荷重のことを指す場合が圧倒的に多いようなので、
ここでは「ステップ荷重」を使っておく。
ヘビサイドの階段関数の場合、$0$から$1$へ切り変わる境界を$t\lt 0$までと$t\gt 0$からに
しているが、この他にも、
$t\lt 0$と$t\ge 0$とか
$t\gt 0$と$t\le 0$とか、
階段関数の定義にはいろいろとある。
今回は、$t=0$での初期条件を使いたい関係上、以下のように定義される
ステップ荷重が減衰のない1自由度系の質点に載荷された問題を考える。
$f(t)=
\begin{cases}
0 & \;\;\;\;(t\le 0)\\
P & \;\;\;\;(t\gt 0)
\end{cases}
$
減衰なしの1自由度系の運動方程式は、
$m\ddot{v}(t)+kv(t)=f(t)$
で表されるから、
$t\gt 0$での運動方程式は、
$m\ddot{v}(t)+kv(t)=P$
ただし、$v(0)=0, \;\;\dot{v}(0)=0$
ここで、任意の外力に対する応答は以下の畳込み積分で表されるから
${\displaystyle v(t)=\int_{0}^{\infty}f(\tau)v_{単}(t-\tau)d\tau}\\
{\displaystyle =\int_{0}^{\infty}
\frac{f(\tau)}{m\omega}
H(t-\tau)\sin\omega(t-\tau)
d\tau}$
これに$f(\tau)=P$を代入し、積分区間を以下のように$t$で分割してみる。
${\displaystyle v(t)=
\int_{0}^{t}
\frac{P}{m\omega}
H(t-\tau)\sin\omega(t-\tau)
d\tau
+
\int_{t}^{\infty}
\frac{P}{m\omega}
H(t-\tau)\sin\omega(t-\tau)
d\tau
}$
ヘビサイドの階段関数$H(t-\tau)$は、
$H(t-\tau)=
\begin{cases}
0 & \;\;(t\lt \tau)\\
1 & \;\;(t\gt \tau)
\end{cases}
$
で表されるが、上の積分は$\tau$についての積分で、
$\tau$が$t$より小さいか大きいかで積分区間が分けられているから、
$\tau\lt t$となる第1項の$H(t-\tau)$は$1$となり、
$\tau\gt t$となる第2項の積分は消え、
${\displaystyle v(t)=
\int_{0}^{t}
\frac{P}{m\omega}
\sin\omega(t-\tau)
d\tau
}$
となる。
「$t$が$\tau$より小さいと$0$」を「$\tau$が$t$より大きいと$0$」に
読み変えるあたりは、なんか、違和感があるかもしれないが
(ヘビサイド関数は$t$の小さい方が$0$なのに、
$\tau$で積分すると$\tau$の大きい方が$0$になる辺りに)、
ヘビサイド関数の面白いところだ。積分を実行すると、
$
{\displaystyle
v(t)=\left[
\frac{P}{m\omega^{2}}
\cos\omega(t-\tau)
\right]_{0}^{t}
=
\frac{P}{m\omega^{2}}
(1-\cos\omega t)
}
$
${\displaystyle \omega^{2}=\frac{k}{m}}$だから、
${\displaystyle v(t)=\frac{P}{k}(1-\cos\omega t)}$
となる。
ステップ荷重の最大値$P$が静的に載荷された場合の変位$v_{静}$を、
$v_{静}=\dfrac{P}{k}$
とすると、
$v(t)=v_{静}(1-\cos\omega t)$
と表せ、
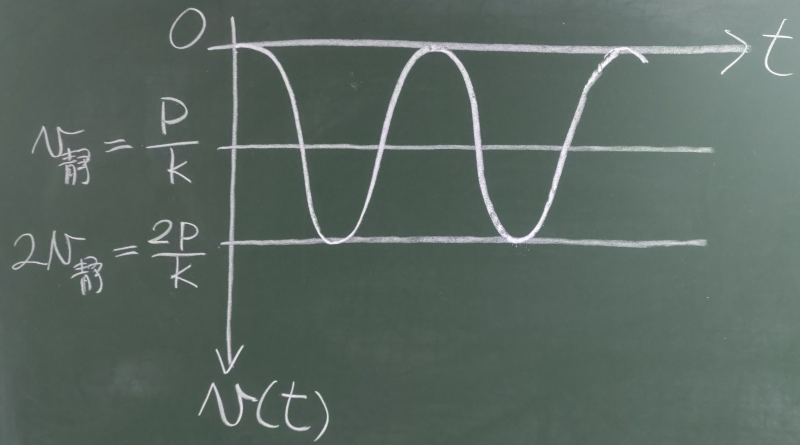ステップ荷重$P$が静的に載荷された場合のつりあい位置($v_{静}=\frac{P}{k}$)を
振動の中心として、ステップ荷重載荷前の静的つりあい位置($v(0)=0$)から
ステップ荷重が静的に載荷された場合のつりあい位置($v_{静}=\frac{P}{k}$)までの距離
($\frac{P}{k}$)を振幅とする振動をしているということになる。
なお、この問題は、運動方程式を変形して$V=v-\frac{P}{k}$みたいにおいて、
$V$についての微分方程式に書き換えると$P$が消えて
自由振動の解が利用できるから、畳み込み積分をやらなくても求まる。
さてここで、
${\displaystyle DAF=\frac{v(t)}{v_{静}}}$
で定義されるDAF(Dynamic Amplification Factor)を
求めてみる。
上で求めた
$M_{D}$(Dynamic Magnification Factor, 略してDMF)とは違うので注意
($M_{D}$は、強制外力の関数の部分を取り除いた増幅率)。
日本語では、どちらも「動的増幅率」というので紛らわしい。
$DAF$の最大値$DAF_{max}$は、衝撃係数として使われたりするので重要である。
$DAF_{max}$のことを$DAF$と定義する場合の方が多いかもしれない。
$DLF$(Dynamic Load Factor)動荷重係数という場合もある。
例えば、
金沢大学機械機能設計研究室の資料(
衝撃応答・破壊の基礎)では、
${\displaystyle DLF=\frac{v(t)}{v_{静}}}$
と定義して、$DLF_{max}=2$としている。
$v_{静}$というのは、例えば吊り橋のケーブルが切れたといった
外力の変化が、静的に載荷された場合の変位のことで、
時刻$t=0$以降に$P$のステップ荷重が載荷されるこの問題では、
${\displaystyle v_{静}=\frac{P}{k}}$
となる。
橋梁のケーブル破断の場合、ケーブルが切れていない
健全時の状態を変位$v(t)$の基準にとれば、上記の式で$DAF$を求めていいと思うが、
死荷重や活荷重の載荷前とか、別の状態を変位の基準にしていた場合には、
${\displaystyle DAF=\frac{v(t)-v_{健}}{v_{静}-v_{健}}}$
みたいにして健全時の状態を基準とした変位の比になるように式を書き換えなければならなかったりする
(例えば、ばねの自然長を変位の基準にとって、ばねが切れた場合)
ので、$DAF$の定義は、その辺の事情に応じて、いくつか種類があるようだ。
さて今回の$DAF$は、
$DAF=\dfrac{v(t)}{v_{静}}=1-\cos\omega t$
となるので、その最大値は
$\omega t=(2n-1)\pi$のときであり、
$DAF_{max}=2$
となる。
変位の基準はステップ荷重載荷前の$v(0)=0$のところにあり、
ステップ荷重が静的に載荷された場合のつりあい位置($v_{静}=\frac{P}{k}$)を
振動の中心にして、
$v(0)=0$から$v_{静}=\frac{P}{k}$までの距離
($\frac{P}{k}$)を振幅とする振動をしているから、
最大変位は$2v_{静}$となり、$\frac{v(t)}{v_{静}}$で定義される
$DAF$の最大値は2となる。
次に、減衰を考慮した場合のステップ荷重に対する応答を考えてみる。
減衰ありの場合、
時刻$t=\tau$に単位衝撃荷重を受けた際の単位衝撃応答$v_{単}(t-\tau)$は、
$v_{単}(t-\tau)=
\frac{e^{-\beta\omega(t-\tau)}
}{m\omega_{d}}
H(t-\tau)\sin\omega_{d}(t-\tau)$
だったから、減衰なしでやったのと同様の畳み込み積分で表現すれば、
$\tau\lt t$の積分区間で$H(t-\tau)=1$となり、
$\tau\gt t$の積分区間で$H(t-\tau)=0$となることにより、たぶん、
${\displaystyle v(t)=
\int_{0}^{t}
\frac{Pe^{-\beta\omega(t-\tau)}
}{m\omega_{d}}
\sin\omega_{d}(t-\tau)}
d\tau$
と表せる。部分積分を使って計算していくと、
${\displaystyle v(t)=
\left[
\frac{Pe^{-\beta\omega(t-\tau)}
}{\beta\omega m\omega_{d}}\sin\omega_{d}(t-\tau)
\right]_{0}^{t}
+
\int_{0}^{t}
\frac{Pe^{-\beta\omega(t-\tau)}
}{\beta\omega m}
\cos\omega_{d}(t-\tau)
d\tau
}$
${\displaystyle v(t)
=
-\frac{Pe^{-\beta\omega t}
}{\beta\omega m\omega_{d}}\sin\omega_{d}t
+
\left[
\frac{Pe^{-\beta\omega(t-\tau)}
}{\beta^{2}\omega^{2}m}
\cos\omega_{d}(t-\tau)
\right]_{0}^{t}
-
\int_{0}^{t}
\frac{\omega_{d}Pe^{-\beta\omega(t-\tau)}
}{\beta^{2}\omega^{2}m}
\sin\omega_{d}(t-\tau)d\tau
}$
${\displaystyle v(t)
=
-\frac{Pe^{-\beta\omega t}
}{\beta\omega m\omega_{d}}\sin\omega_{d}t
+
\frac{P}
{\beta^{2}\omega^{2} m}(1-e^{-\beta\omega t}\cos\omega_{d}t)
-\frac{\omega_{d}^{2}}{\beta^{2}\omega^{2}}
v(t)
}$
${\displaystyle
\left(\beta^{2}+\frac{\omega_{d}^{2}}{\omega^{2}}\right)v(t)
=
-\frac{Pe^{-\beta\omega t}
}{\omega m\omega_{d}}\beta\sin\omega_{d}t
+
\frac{P}
{\omega^{2} m}(1-e^{-\beta\omega t}\cos\omega_{d}t)
}$
$\omega_{d}^{2}=\omega^{2}(1-\beta^{2})$より、
${\displaystyle
v(t)
=
\frac{P}
{\omega^{2} m}(1-e^{-\beta\omega t}
(
\frac{\omega}{\omega_{d}}\beta\sin\omega_{d}t
+
\cos\omega_{d}t)
)
}$
$\omega^{2}=\frac{k}{m}$より、
${\displaystyle
v(t)
=
\frac{P}
{k}(1-e^{-\beta\omega t}
(
\frac{\omega}{\omega_{d}}\beta\sin\omega_{d}t
+
\cos\omega_{d}t)
)
}$
熊大機械の
鳥越 一平先生の授業関係資料の
過渡振動で求められている結果とも合ってるようなので、
たぶん合ってるかと思う。
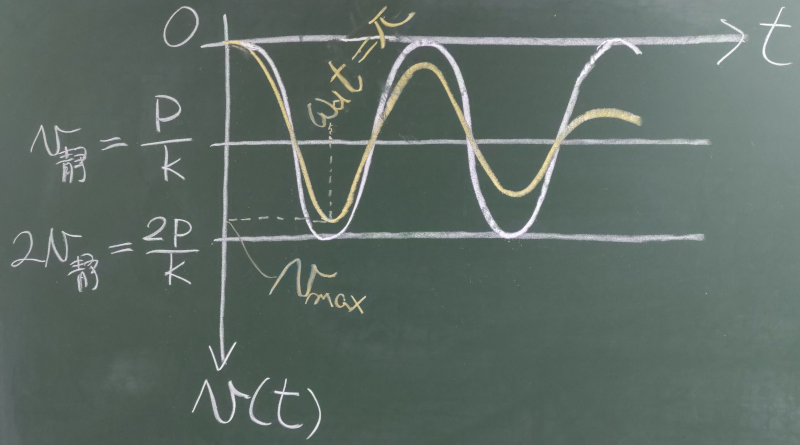変位の基準はステップ荷重載荷前の$v(0)=0$のところにあり、
ステップ荷重が静的に載荷された場合のつりあい位置($v_{静}=\frac{P}{k}$)を
振動の中心にして、
$v(0)=0$から$v_{静}=\frac{P}{k}$までの距離
($\frac{P}{k}$)を初期の振幅として、段々と減衰していくから、
最大変位は$\omega_{d}t=\pi$となるときで、
$2v_{静}$よりはやや小さめの値となる。
さて、$DAF$を求めてみると、$v_{静}=\frac{P}{k}$だから、
$DAF={\displaystyle \frac{v(t)}{v_{静}}}
=
1-e^{-\beta\omega t}(\frac{\omega}{\omega_{d}}\beta\sin\omega_{d}t+\cos\omega_{d}t)$
となるから、
これの最大値$DAF_{max}$は、$\omega_{d}t=\omega t\sqrt{1-\beta^{2}}=\pi$のときで、
${\displaystyle DAF_{max}=
1+e^{-\beta\pi/\sqrt{1-\beta^{2}}}
}$
となる。仮に$\beta=0.05$を代入すると、
$DAF_{max}=
1+e^{-0.05\pi/\sqrt{1-0.05^{2}}}=1.8544678930$
となる。
ケーブル破断等の衝撃係数として多用される1.854は、
減衰定数0.05の1自由度系にステップ荷重を作用させた際の$DAF$の最大値から求めている
ということなので、
この値のことだと思う。
ちなみに、1.854の出典とされているのは、以下の文献だが、秋田大学その他
の図書館等ではどうも入手困難なので確認していない。
Fatigue evaluation and redundancy analysis : Bridge No. 9340, I-35W over Mississippi River
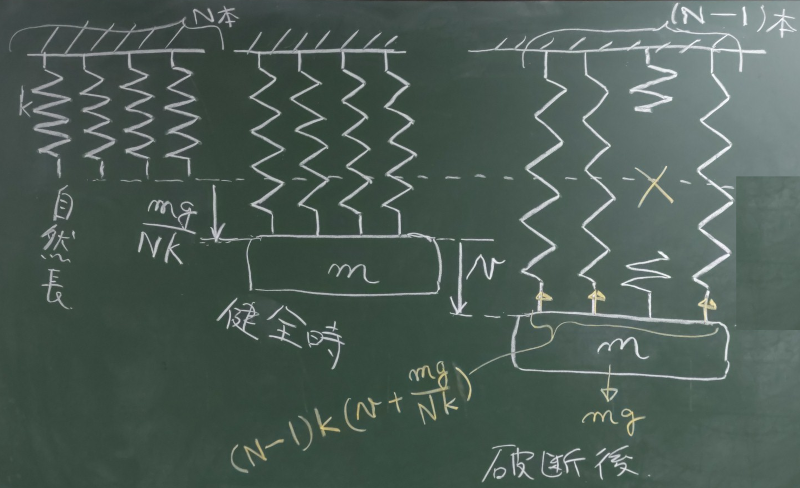$N$本のばねに質量$m$の重りがくっついていて、
$t\le 0$では静止状態（健全時）、$t\gt 0$ではばねが1本切れていることにする。
つまり、合成ばねのばね定数を$K(t)$とすると、
$K(t)=
\begin{cases}
Nk & \;\;\;\;(t\le 0)\\
(N-1)k & \;\;\;\;(t\gt 0)
\end{cases}
$
となる。$t\le 0$でばねがまだ切れずに静的につりあっている状態を
「健全時」として、この位置をおもりの変位$v(t)$の基準とする。
$t\gt 0$でばねが1本切れた状態の運動方程式を考えてみる。
自然長からのばねののびは、
健全時を基準とした$v$に、自然長から健全時までの伸び$v_{健}=\frac{mg}{Nk}$を
足した$v+\frac{mg}{NK}$で表される。
ばねに作用する力は、この自然長からの伸びに、
$(N-1)$本のばねのばね定数$(N-1)k$をかけたものとなるから、運動方程式は、
以下のように表される。
$\sum\downarrow = m\ddot{v}(t)$
$mg-(N-1)k\left(v(t)+\frac{mg}{Nk}\right)=m\ddot{v}(t)$
$m\ddot{v}(t)+(N-1)k\left(v(t)+\frac{mg}{Nk}\right)=mg$
これを変形すると
$m\ddot{v}(t)+(N-1)kv(t)+\frac{N-1}{N}mg=mg$
$m\ddot{v}(t)+(N-1)kv(t)=\frac{mg}{N}$
これとステップ荷重$P$の
場合の以下の運動方程式と比べてみる。
$m\ddot{v}(t)+kv(t)=P$
$k$を$(N-1)k$に、$P$を$\frac{mg}{N}$に置き換えた式になっているから、
$N$本のばねが1本切れる問題は、
$(N-1)$本のばねにくっついた重りに、
$\frac{mg}{N}$のステップ荷重(ばねが1本切れた前後の荷重の変化)
が作用した問題と同じだということになりそうだ
(ただし、変位の基準は$N$本のばねがある健全時だから、
$(N-1)$本のばねに質量$m$の重りをくっつけてつりあった状態から、
$N$本のばねでつりあう健全時の状態まで
上に持ち上げておいて、そうすると重りに上向きに$\frac{mg}{N}$の
力を静的に載荷していることになるが、
$t\gt 0$でこれがなくなるというか下向きに$\frac{mg}{N}$のステップ荷重が載荷されて
キャンセルされる問題ということになるだろうか。
そのうち、もう少し考察してみる)。
そうすると、ステップ荷重$P$の変位
$v_{ステップ}(t)=\frac{P}{k}(1-\cos\omega t)$
の$P$を$\frac{mg}{N}$に、$k$を$(N-1)k$に置き換えたものが、
変位ということになるから、
$v(t)=\frac{mg}{N(N-1)k}(1-\cos\omega t)$
となる。
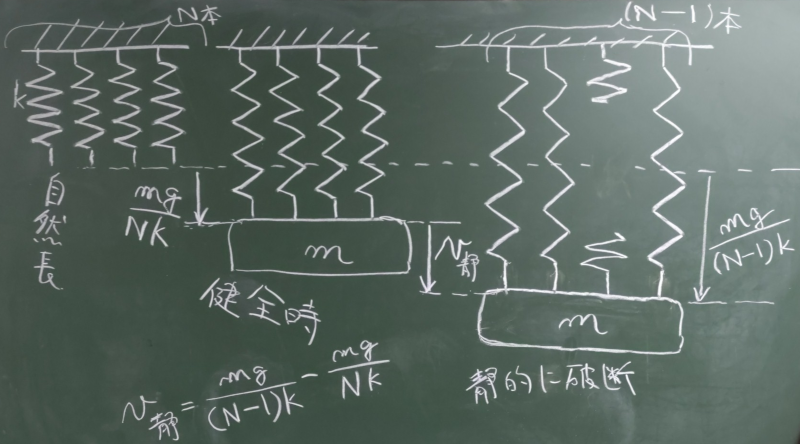ばねが切れた状態での静的なつりあい位置での変位$v_{静}$は、
$(N-1)$本のばねにおもり$m$を静的に載荷した場合の
自然長からの変位$\frac{mg}{(N-1)k}$
と
$N$本のばねにおもり$m$を静的に載荷した場合の
自然長からの変位$\frac{mg}{Nk}$との差だから、
$v_{静}=\frac{mg}{(N-1)k}-\frac{mg}{Nk}=\frac{mg}{N(N-1)k}$
つまり、$v_{静}$を使って書けば、
$v(t)=v_{静}(1-\cos\omega t)$
ということになる。
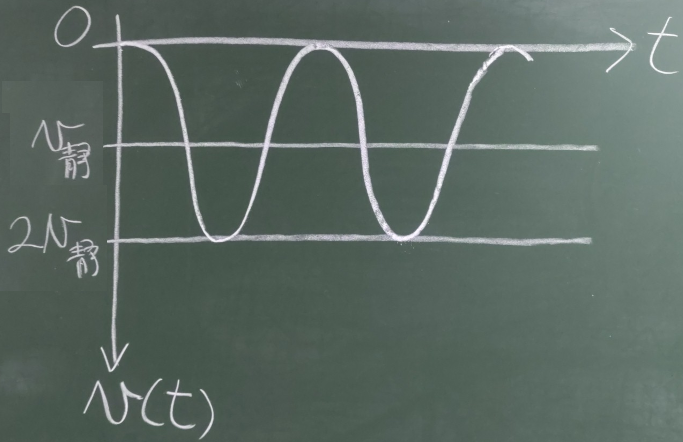ばねの破断後の振動は、破断後の静的つりあい位置($v_{静}$)を振動の中心にして、
健全時($v(0)=0$)から$v_{静}$までの距離を振幅とする振動をするということになる。