以下の話の流れや導出方法等は、 後藤の恩師の岩熊先生と後輩の小山さんとの共著： 岩熊哲夫・小山茂『鬆徒労苦衷有迷禍荷苦痛-- 計算機による構造解析の基礎としての構造力学を独習する』 の 10.3 連続体の振動 のやり方を参考にしています。 まだ、準備開始したばかりなので、間違いとか、それなりにあるかもしれません。 大幅に書き換える可能性もあります。

目次

• 2自由度系の振動
• 自由振動(減衰なし)

事前に確認しておきたい数学の基礎知識

オイラーの公式：
$e^{ix}=\cos x+i\sin x$
$e^{-ix}=\cos x-i\sin x$
これを連立させると以下が得られる。
$\sin x=\dfrac{e^{ix}-e^{-ix}}{2i},\;\; \cos x=\dfrac{e^{iz}+e^{-ix}}{2}$

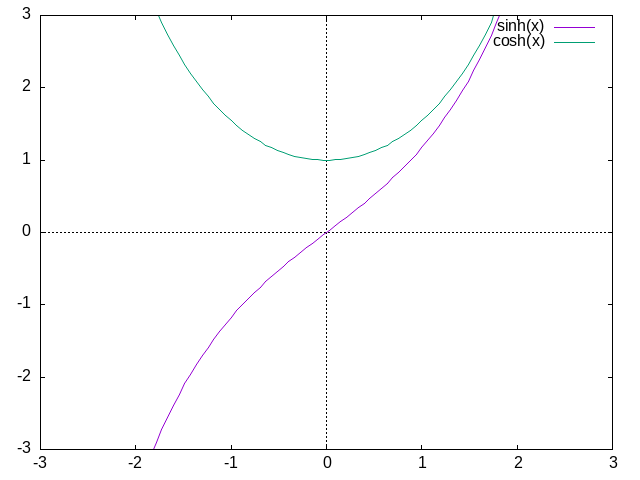
双曲線関数
$\sinh(x)=\dfrac{e^{x}-e^{-x}}{2},\;\; \cosh(x)=\dfrac{e^{x}+e^{-x}}{2}$
$(\sinh(x))'=\cosh(x),\; \;(\cosh(x))'=\sinh(x)\;$
ちなみに、なぜ双曲線関数と言うのかというと、 $x=\cos\theta,\;\; y=\sin\theta$とおくと、単位円の式$x^{2}+y^{2}=1$を満たすが、 $x=\cosh\theta,\;\; y=\sinh\theta$とおくと、$x^{2}-y^{2}=1$となる 双曲線の式を満たす。 (Wikipedia)

弦の振動

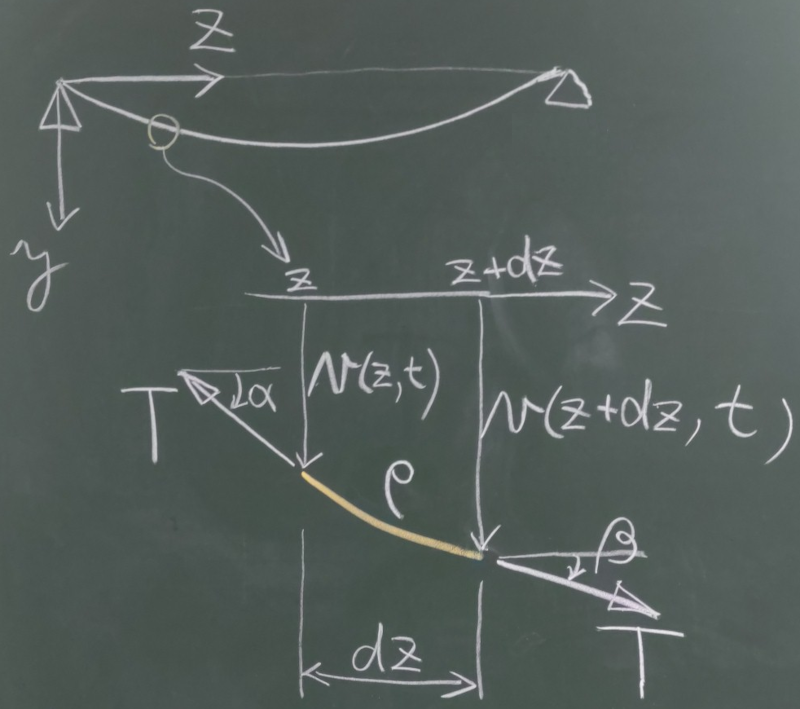弦とか梁とかの振動を考える。 弦とか梁というのは、連続体であり、あらゆる点$z$に対する変位$v(z)$が あるので、自由度が無限にある無限自由度と考えられる。 なので、変位$v$は、座標$z$と時刻$t$の関数として$v(z,t)$と表すことにする。 まずは、弦の振動から考えていこう。 弦というのは曲げ剛性がなく、張力がないとたるんでしまい、 自立しない。 なので、一定の張力$T$で張られた弦が弾かれて自由振動する状態を考える。 長さ$dz$の微小部分を取り出して、 下方向を正として鉛直方向の運動方程式をたててみる。 簡単のため、重力は無視する。
$\sum\downarrow =\rho Adz\dfrac{\partial^{2}v(z,t)}{\partial t^{2}}\\ -T\sin\alpha +T\sin\beta =\rho Adz\dfrac{\partial^{2}v(z,t)}{\partial t^{2}} $
ただし、$\rho$は弦の密度、$A$は弦の断面積、 $\alpha$と$\beta$は 微小部分の 左端と右端における変位$v$の傾き である。 $z$が正方向に増えるときの$v(z)$の傾きを表すためにこの向きにしたが、 $x$軸回りに左ねじ回転になっているので、 もし右ねじ回転角$\theta_{x}$との関係で書く必要がある場合には、 $\alpha=-\theta_{x}(z,t)$みたいになる。 $\alpha$と$\beta$は微小であり、下方向変位$v(z,t)$の$z$軸に対する傾きで 表せるので、
$\sin\alpha\simeq \alpha = \dfrac{\partial v(z,t)}{\partial z}$
$\sin\beta\simeq \beta = \dfrac{\partial v(z+dz,t)}{\partial z} = \dfrac{\partial v(z,t)}{\partial z} +\dfrac{\partial^{2}v(z,t)}{\partial z^{2}}dz $
となる。 $z$についての微分だが、 $v$が$z$と$t$の関数なので、偏微分で表している。 $z$から$dz$だけ離れたところの傾き$\beta$を$z$での傾き$\alpha$から どれだけ変化しているかで見積もるには、 $\alpha +\frac{\partial\alpha}{\partial z}dz$みたいにすればいいことは、 応力のつりあいのところで説明している。 要はテイラー展開の2項目までとったということ。 $\sin\alpha, \;\sin\beta$を上の運動方程式に代入して 両辺を$dz$で割ると、
$ T\dfrac{\partial^{2}v(z,t)}{\partial z^{2}} =\rho A\dfrac{\partial^{2}v(z,t)}{\partial t^{2}} $
となる。
$c=\sqrt{\dfrac{T}{\rho A}}$
とおくと、
$ \dfrac{1}{c^{2}}\dfrac{\partial^{2}v(z,t)}{\partial t^{2}} =\dfrac{\partial^{2}v(z,t)}{\partial z^{2}} $
のような形の運動方程式になるが、 この式は1次元の波動方程式と呼ばれ、 $c$は波速(波の特定の点が移動する速度)つまり位相速度を表す。 海岸工学とかで出てくる1次元の波動方程式と比べてみてほしい。 たぶん同じような形ではないかと思う。

両端固定の自由振動

ギターの弦の振動みたいな 両端固定の自由振動を考えよう。 弦の場合、両端固定とはいっても曲げ剛性がないので、 端部でたわみ角が発生するから、 両端ヒンジと捉えてもいいし、単純梁のローラー支障側を$T$で引っ張って 張力$T$を発生させていると考えてもいい。 弦の左端を$z=0,\;$ 弦の右端を$z=\ell$とすると、 境界条件は、
$v(0,t)=0,\;\; v(\ell,t)=0$
で与えられる。 ギターの弦の振動のように、定在波(定常波)で振動している状態を考えると、 波の形(モード)はどの時刻でも同じで、 時刻によってその形に対する倍率が違うだけだから、 空間的な変動と時間的な変動を分離して$v(z,t)$を以下のように置いてみよう。
$v(z,t)=y(z)a(t)$
$y(z)$は波の形(振動モード)を表していることになる。 上の波動方程式に代入すると
$ \dfrac{y(z)}{c^{2}}\dfrac{\partial^{2}a(t)}{\partial t^{2}} =a(t)\dfrac{\partial^{2}y(z)}{\partial z^{2}} $
となるから、$t$についての微分を$^{\cdot}$で、 $z$についての微分を$'$で表すと、
$ \dfrac{y''(z)}{y(z)}=\dfrac{\ddot{a}(t)}{c^{2}a(t)} $
となる。 左辺が$z$だけの関数で、右辺が$t$だけの関数で、 この等式が任意の$z$と$t$について成り立つには、 両辺とも定数である必要があるので、
$ \dfrac{y''(z)}{y(z)}=\dfrac{\ddot{a}(t)}{c^{2}a(t)}=\kappa $
とおく。$\kappa$は定数。すると、
$y''(z)-\kappa y(z)=0$
$\ddot{a}(t)-\kappa c^{2}a(t)=0$
の2つの微分方程式が得られる。 まずは、
$y''(z)-\kappa y(z)=0$
の方から考える。 1自由度系の振動のところで、 $\ddot{v}(t)+\omega^{2}v(t)=0$の形の微分方程式の一般解は、 $v(t)=A\sin\omega t+B\cos\omega t$と求まることがわかっているから、 $\kappa\lt 0$なら解けそうだが、まずは$\kappa \gt 0$の場合を考えてみる。
$\kappa \gt 0$の場合
$\kappa =\alpha^{2}$とおくと、
$y''(z)-\alpha^{2}y(z)=0$
となる。
$y(z)=e^{\lambda z}$とおくと、
$y'(z)=\lambda e^{\lambda z}$
$y''(z)=\lambda^{2} e^{\lambda z}$
これらを、 $y''(z)-\alpha^{2}y(z)=0$に代入すると、
$(\lambda^{2}-\alpha^{2})e^{\lambda z}=0$
となり、これがすべての$z$になりたつことから、特性方程式
$\lambda^{2}-\alpha^{2}=0$
が得られる。この解は、
$\lambda=\pm\alpha$ となり、
一般解は、独立な解$e^{\alpha z}$, $\;e^{-\alpha z}$の線形結合 ということで
$y(z)=C_{1}e^{\alpha z}+C_{2}e^{-\alpha z}$
となる。$C_{1}, \;C_{2}$は任意の定数。 これを以下のように変形する。
$y(z)= (C_{1}+C_{2})\dfrac{e^{\alpha z}+e^{-\alpha z}}{2} +(C_{1}-C_{2})\dfrac{e^{\alpha z}-e^{-\alpha z}}{2} $
ここで、$A=C_{1}-C_{2}, \; B=C_{1}+C_{2}$とおきかえると、一般解は、 以下のように書き換えられる。
$y(z)=A\sinh\alpha z+B\cosh\alpha z$
$A,\; B$は任意の定数。 $\sinh,\; \cosh$は次式で与えられる双曲線関数で、
$\sinh(x)=\dfrac{e^{x}-e^{-x}}{2},\;\; \cosh(x)=\dfrac{e^{x}+e^{-x}}{2}$
それぞれ、2回微分すると $(\sinh(x))''=\sinh(x)\;$, $(\cosh(x))''=\cosh(x)\;$と 元に戻るので、$y''-\alpha^{2}y=0$みたいな式の一般解は このように与えられることは各自 確認してほしい。 さて、境界条件 $v(0,t)=0,\;\; v(\ell,t)=0$は、 任意の$t$で成り立つから、$y(0)=0$, $y(\ell )=0$と変数分離できる。 これを一般解に代入すると、
$y(0)=A\sinh(0)+B\cosh(0)=B=0$
$y(\ell )=A\sinh\alpha\ell=0$
今、$\kappa=\alpha^{2}\gt 0$だから、 $\alpha\ell\ne 0$で、$\sinh\alpha\ell\ne 0$なので、$A=0$となる。 つまり、$y(z)=0$となり、意味のある解ではない。
$\kappa =0$の場合
$y''(z)=0$
を解くと、
$y(z)=Az+B$
となる。$A,\;B$は任意の定数。境界条件を代入すると、
$y(0)=B=0$
$y(\ell )=A\ell=0$
となり、これも$y(z)=0$となって意味のある解ではない。
$\kappa \lt 0$の場合
$\kappa =-\alpha^{2}$とおくと、
$y''+\alpha^{2}y(z)=0$
となるが、これの一般解は 1自由度系の振動のところで 求めたように、
$y(z)=A\sin\alpha z+B\cos\alpha z$
と求まる。 $A, \;B$は任意の定数。 境界条件を代入すると、
$y(0)=B=0$
$y(\ell )=A\sin\alpha\ell =0$
となる。 意味のある解となるためには$A\ne 0$とならなければならないから、 $\sin\alpha\ell =0$でなければならない。 つまり、
$\alpha\ell=n\pi \;\;\;(n=1,2,3,...)$
であり、$\alpha=\dfrac{n\pi}{\ell}$だから、
$y_{n}(z)=A_{n}\sin(\dfrac{n\pi z}{\ell}) \;\;\;(n=1,2,3,...)$
が解となる。 $A\ne 0$は不定である。 両端固定の弦の振動は、両端の変位$0$の境界条件を満たす 正弦波の振動をしていて、 $n=1$で$\sin$ 1半波（さいんいちはんぱ）、 $n=2$で$\sin$2半波（さいんにはんぱ）、、、 のように$n$の次数ごとに対応する振動モードが存在する (正弦1半波、正弦2半波、、、みたいな言い方もある）。

次に
$\ddot{a}(t)-\kappa c^{2}a(t)=0$
の方を考える。 $\kappa =-\alpha^{2}$を代入すると、
$\ddot{a}(t)+(\alpha c)^{2}a(t)=0$
となるから、一般解は上と同様に、
$a(t)=C\sin\alpha ct+D\cos\alpha ct$
と求まる。 $C, \;D$は任意の定数。 $\alpha=\dfrac{n\pi}{\ell}$を代入すれば、
$a_{n}(t)=C_{n}\sin\dfrac{n\pi ct}{\ell}+D_{n}\cos\dfrac{n\pi ct}{\ell} \;\;\;(n=1,2,3,...)$
となる。 さて、 $v(z,t)=y(z)a(t)$ だったが、$y(z)$も$a(t)$も$n=1,2,3,...$に対して無限の解$y_{n}(z),\; a_{n}(t)$が 存在するので、 それらがすべて重ね合わされた解は、
${\displaystyle v(z,t)= \sum_{n=1}^{\infty} A_{n}\sin(\dfrac{n\pi z}{\ell}) (C_{n}\sin\dfrac{n\pi ct}{\ell}+D_{n}\cos\dfrac{n\pi ct}{\ell}) }$
$A_{n},\;B_{n},\;C_{n}$は定数で $v(z,0)$と$\dot{v}(z,0)$の2つの初期条件から決まるが、 $F_{n}=A_{n}C_{n},\;G_{n}=A_{n}D_{n}$と置き直すと
${\displaystyle v(z,t)= \sum_{n=1}^{\infty} \sin(\dfrac{n\pi z}{\ell}) (F_{n}\sin\dfrac{n\pi ct}{\ell}+G_{n}\cos\dfrac{n\pi ct}{\ell}) }$
となる。$\sin,\;\cos$の中で$t$にかけてある部分が 固有角振動数になるから、$n$次モードの 固有角振動数$\omega_{n}$を
$\omega_{n}=\dfrac{n\pi c}{\ell}=\dfrac{n\pi}{\ell}\sqrt{\dfrac{T}{\rho A}} \;\;\;\; (n=1,2,3,...)$
と置くと
${\displaystyle v(z,t)= \sum_{n=1}^{\infty} \sin(\dfrac{n\pi z}{\ell}) (F_{n}\sin\omega_{n}t+G_{n}\cos\omega_{n}t) }$
となる。 これに初期条件を代入して解くには、 モードの直交性の話をしなければならないので、 ここではやらない。 モードの直交性がどういうものかについては、 岩熊哲夫・小山茂『鬆徒労苦衷有迷禍荷苦痛-- 計算機による構造解析の基礎としての構造力学を独習する』 の 10.4.4 振動モードの直交性と自由振動解--モード解析法 を参照。 両端固定の$v(z,t)$に初期条件を代入して、 モードの直交性を用いて具体的に解いている例としては、 山口大学 齊藤 俊 先生の 11．連続体の振動問題Ⅰ（弦の横振動） を参照。
さて、ここで解いた2つの微分方程式は、
$y''(z)+\alpha^{2}y(z)=0$
$\ddot{a}(t)+(\alpha c)^{2}a(t)=0$
で、$\alpha c=\dfrac{n\pi c}{\ell}=\omega_{n}$だから、
$y''(z)+\alpha^{2}y(z)=0$
$\ddot{a}(t)+\omega_{n}^{2}a(t)=0$
みたいな形の微分方程式で、 1自由度系の振動のところや 構造力学IIのオイラー座屈のところで 出てきた。 オイラー座屈では、$\alpha=\dfrac{n\pi}{\ell}$となるところも共通している。 実は、 これらは微分方程式の固有値問題になっていて、 $\alpha^{2}$や$\omega_{n}^{2}$が固有値、 $y_{n}(z)$や$a_{n}(t)$が固有関数に対応している。 より厳密には、 スツルム＝リウヴィルの固有値問題 の一種ではないかと思う。 2自由度系の振動のところとか、 主応力のところとか、 行列の固有値問題として解かれる問題は多いが、 振動や座屈の問題では微分方程式の固有値問題として解かれる問題も多い。 行列の固有値問題は、
$\mathbf{A}\mathbf{y}=\lambda\mathbf{y}$
を満たす$\mathbf{0}$でない$\mathbf{y}$が存在するような固有値$\lambda$ を求める問題なのに対し、 微分方程式の固有値問題は、
$\dfrac{d^{2}}{dz^{2}}y=\lambda y$
みたいな形の微分方程式を満たす$0$でない$y$が存在するような 固有値$\lambda$を求める問題という意味で、 似たような形をしている。
今回の問題では、 固有関数 $y_{n}(z)=A\sin(\dfrac{n\pi z}{\ell})$が振動モードに対応し、 固有値の平方根$\omega_{n}$が固有角振動数に対応しているが、 構造力学IIのオイラー座屈の問題では、 固有値(に曲げ剛性$EI$をかけたもの)が座屈荷重に対応し、 固有関数が座屈モードに対応していると考えられる。 このように、構造系の様々な問題は固有値問題として表されるものが多い。

梁の振動

次に、梁の振動を考える。 構造力学の梁のモデルを 拡張し、 座標$z$, 時刻$t$でのせん断力が$S(z,t)$, 曲げモーメントが$M(z,t)$, 鉛直分布荷重が$q(z,t)$で表されることにする。 簡単のため軸力や軸方向分布外力はないものとし、 $N(z,t)=0, \; p(z,t)=0$とする。 減衰もないものとし、 重力も無視する。 弦の振動と同様に 長さ$dz$の微小部分を取り出して、 下方向を正として鉛直方向の運動方程式をたててみる。
$\sum\downarrow =\rho Adz\dfrac{\partial^{2}v(z,t)}{\partial t^{2}} $
左辺の鉛直下方向の力の合計を書き下すと、以下のようになる。 左の切断面の$S(z,t),\; M(z,t)$から右の切断面の値を テイラー展開の2項目までで近似するのは 弦の振動と同様。 構造力学の梁のモデル参照。
$-S(z,t)+q(z,t)dz +S(z,t)+\dfrac{\partial S(z,t)}{\partial z}dz =\rho Adz\dfrac{\partial^{2}v(z,t)}{\partial t^{2}} $
つまり、
$ \dfrac{\partial S(z,t)}{\partial z} +q(z,t) =\rho A\dfrac{\partial^{2}v(z,t)}{\partial t^{2}} $
構造力学の梁のモデルでも 導いた通り、モーメントのつりあいから、 せん断力$S(z,t)$は、
$S(z,t)=\dfrac{\partial M(z,t)}{\partial z}$
と表されるから、
$ \dfrac{\partial^{2} M(z,t)}{\partial z^{2}} +q(z,t) =\rho A\dfrac{\partial^{2}v(z,t)}{\partial t^{2}} $
となる。 また、 構造力学の梁モデルで 導いたように、$z$が断面の図心を通る場合は、
$M(z,t)=-EI \dfrac{\partial^{2} v(z,t)}{\partial z^{2}} $
で表せるから、
$\rho A\dfrac{\partial^{2}v(z,t)}{\partial t^{2}} + EI\dfrac{\partial^{4} v(z,t)}{\partial z^{4}} =q(z,t) $
となる。

単純梁の自由振動

単純梁の自由振動を考えよう。 外力はないので$q(z,t)=0$だから、
$-\rho A\dfrac{\partial^{2}v(z,t)}{\partial t^{2}} = EI\dfrac{\partial^{4} v(z,t)}{\partial z^{4}} $
となる。 梁の左端を$z=0,\;$ 梁の右端を$z=\ell$とすると、 単純梁の 境界条件は、両端でたわみと曲率(モーメント)が$0$なので
$v(0,t)=0,\;\; v''(0,t)=0,\;\; v(\ell,t)=0, \;\; v''(\ell,t)=0 $
で与えられる。 弦の振動のときと同じように、 梁が固有振動モードで自由振動している状態を考えると、 波の形(モード)はどの時刻でも同じで、 時刻によってその形に対する倍率が違うだけだから、 空間的な変動と時間的な変動を分離して$v(z,t)$を以下のように置いてみよう。
$v(z,t)=y(z)a(t)$
これを上の運動方程式に代入すると、
$-\rho Ay(z)\ddot{a}(t)=EIy''''(z)a(t) $
となるから、
$ -\dfrac{\ddot{a}(t)}{a(t)}=\dfrac{EI}{\rho A}\dfrac{y''''(z)}{y(z)} $
となる。 左辺が$z$だけの関数で、右辺が$t$だけの関数で、 この等式が任意の$z$と$t$について成り立つには、 両辺とも定数である必要があるので、
$ -\dfrac{\ddot{a}(t)}{a(t)}=\dfrac{EI}{\rho A}\dfrac{y''''(z)}{y(z)} =\kappa $
とおく。$\kappa$は定数。すると、
$y''''(z)-\kappa \dfrac{\rho A}{EI}y(z)=0$
$\ddot{a}(t)+\kappa a(t)=0$
の2つの微分方程式が得られる。 両端固定の弦の自由振動のところで、 $y''(z)-\kappa y(z)=0$の一般解は、 $\kappa\gt 0$だと$\sinh$と$\cosh$の足し算になるから、周期関数にならず、 つまり、 $\kappa\lt 0$のときしか$\sin$と$\cos$で表される周期関数にならない。 つまり(係数が正にしかならないことを2乗を使ってわかりやすく書くなら)、 $y''(z)+\alpha^{2}y(z)=0$みたいな形の式のときに 意味のある解を持つということだ。 さて、今回の梁の問題では、
$\ddot{a}(t)+\kappa a(t)=0$
という式が出てきたが、$a(t)$が周期関数になり、意味のある解を持つためには、 $\kappa$が正でなければならないということになる。ということで、
$\kappa\gt 0$のとき、
$y''''(z)-\kappa\dfrac{\rho A}{EI}y(z)=0$
の方から考える。
$\mu^{4}=\kappa\dfrac{\rho A}{EI}$とおくと、
$y''''(z)-\mu^{4}y(z)=0$
となる。 $y(z)=e^{\lambda z}$とおくと、
$y''''(z)=\lambda^{4} e^{\lambda z}$
これらを、 $y''''(z)-\mu^{4}y(z)=0$に代入すると、
$(\lambda^{4}-\mu^{4})e^{\lambda z}=0$
となり、これがすべての$z$になりたつことから、特性方程式
$\lambda^{4}-\mu^{4}=0$
が得られる。この解は、
$\lambda=\pm\mu, \;\pm i\mu$ となり、
一般解は、独立な解 $e^{\mu z}$, $\;e^{-\mu z}$, $\;e^{i\mu z}$, $\;e^{-i\mu z}$, の線形結合 ということで
$y(z)= C_{1}e^{\mu z}+C_{2}e^{-\mu z} +C_{3}e^{i\mu z}+C_{4}e^{-i\mu z} $
となる。$C_{1}, \;C_{2}, \; C_{3}, \;C_{4}$は任意の定数。 これを以下のように変形する。
$y(z)= (C_{1}+C_{2})\dfrac{e^{\mu z}+e^{-\mu z}}{2} +(C_{1}-C_{2})\dfrac{e^{\mu z}-e^{-\mu z}}{2} +(C_{3}+C_{4})\dfrac{e^{i\mu z}+e^{-i\mu z}}{2} +(C_{3}-C_{4})i\dfrac{e^{i\mu z}-e^{-i\mu z}}{2i} $
ここで、 $A=(C_{3}-C_{4})i, \; B=C_{3}+C_{4}$, $\;C=C_{1}-C_{2}, \; D=C_{1}+C_{2}$ とおきかえると、一般解は、 以下のように書き換えられる。 $A$に$i$が入っているけど、$C_{3}=\frac{B-iA}{2},\;\;C_{4}=\frac{B+iA}{2}$みたいに おけば、$A$は実数定数になるのでは、たぶん。
$y(z)= A\sin\mu z+B\cos\mu z +C\sinh\mu z+D\cosh\mu z $
$A,\; B, \; C, \; D$は任意の定数。ちなみに、三角関数$\sin z, \;\cos z$は 以下のように表せるから、上のような置き換えができるのだ。
$\sin z=\dfrac{e^{iz}-e^{-iz}}{2i}$
$\cos z=\dfrac{e^{iz}+e^{-iz}}{2}$
ちなみに、三角関数がこのように表せることは、オイラーの公式
$e^{iz}=\cos z+i\sin z$
$e^{-iz}=\cos z-i\sin z$
を連立させればわかるので、各自確認。
さて、境界条件を使うため、 一般解を微分して$y''(z)$を求める。
$y(z)= A\sin\mu z+B\cos\mu z +C\sinh\mu z+D\cosh\mu z $
$y'(z)= \mu A\cos\mu z-\mu B\sin\mu z +\mu C\cosh\mu z+\mu D\sinh\mu z $
$y''(z)= -\mu^{2}A\sin\mu z-\mu^{2}B\cos\mu z +\mu^{2}C\sinh\mu z+\mu^{2} D\cosh\mu z $
単純支持の境界条件は$y(z)$について、 $y(0)=0,\; y''(0)=0,\; y(\ell )=0,\; y''(\ell )=0 $がなりたたなければならないから、 これらを代入すると、
$y(0)=B+D=0$
$y''(0)=\mu^{2}(-B+D)=0$
$y(\ell )= A\sin\mu\ell+B\cos\mu\ell +C\sinh\mu\ell+D\cosh\mu\ell=0 $
$y''(\ell )= \mu^{2}(-A\sin\mu\ell-B\cos\mu\ell +C\sinh\mu\ell+D\cosh\mu\ell )=0 $
となるが、まず上の2式を連立させると$B=D=0$だから、下の2式は、
$ A\sin\mu\ell+C\sinh\mu\ell =0 $
$ -A\sin\mu\ell +C\sinh\mu\ell=0 $
となる。つまり、
$ \left( \begin{array}{cc} \sin\mu\ell & \sinh\mu\ell \\ -\sin\mu\ell & \sinh\mu\ell \end{array} \right) \left( \begin{array}{cc} A\\ C \end{array} \right) = \left( \begin{array}{cc} 0\\ 0 \end{array} \right) $
となる。 $A, \; C$がともに$0$以外でこれが成り立つためには、左辺の係数行列の行列式が$0$に ならなければならないので、 $\sin\mu\ell\sinh\mu\ell + \sin\mu\ell\sinh\mu\ell=0$つまり、
$\sin\mu\ell\sinh\mu\ell=0$
が成り立たなければならない。
$\sinh\mu\ell$は$\mu=0$のときしか$0$にならないから、 $\sin\mu\ell=0$でなければならず、
$\mu\ell =n\pi\;\;\;\;\;(n=1,2,3,...)$つまり、
$\mu=\dfrac{n\pi}{\ell}\;\;\;\;\;(n=1,2,3,...)$
となる。 また、$\sin\mu\ell =0$を
$ A\sin\mu\ell+C\sinh\mu\ell =0 $
に代入すると、$C=0$となるから、
$y(z)=A\sin\mu z$
つまり、
$y_{n}(z)=A\sin\dfrac{n\pi z}{\ell}\;\;\;\;\;(n=1,2,3,...)$
となる。 $A$は不定だが、$y(z)$は振動モードを表していて、 振動の形状(モード)が$\sin$波となることがわかる。 というか、この問題も微分方程式 $y''''(z)-\mu^{4}y(z)=0$の固有値問題であり、$\mu^{4}$が固有値、 $y(z)$が固有関数に対応している。

さて、次に
$\ddot{a}(t)+\kappa a(t)=0$
の方を考える。
$\mu^{4}=\kappa\dfrac{\rho A}{EI}$だったから、
$\kappa=\mu^{4}\dfrac{EI}{\rho A} =\left(\dfrac{n\pi}{\ell}\right)^{4}\dfrac{EI}{\rho A}$
となる。これを微分方程式に代入すると、
$\ddot{a}(t)+\left(\dfrac{n\pi}{\ell}\right)^{4}\dfrac{EI}{\rho A}a(t)=0$
ここで、
$\omega_{n}^{2}=\left(\dfrac{n\pi}{\ell}\right)^{4}\dfrac{EI}{\rho A} \;\;\;\;(n=1,2,3,...)$
とおくと、
$\ddot{a}(t)+\omega_{n}^{2}a(t)=0$
となるが、これの一般解は 1自由度系の振動のところで 求めたように、
$a_{n}(t)=F\sin\omega_{n} t+G\cos\omega_{n} t \;\;\;\;(n=1,2,3,...)$
と求まる。 $F, \;G$は任意の定数。
さて、 $v(z,t)=y(z)a(t)$ だったが、$y(z)$も$a(t)$も$n=1,2,3,...$に対して無限の解$y_{n}(z),\; a_{n}(t)$が 存在するので、 それらがすべて重ね合わされた解は、
${\displaystyle v(z,t)= \sum_{n=1}^{\infty} A_{n}\sin(\dfrac{n\pi z}{\ell}) (F_{n}\sin\omega_{n}t+G_{n}\cos\omega_{n}t) }$
$A_{n},\;F_{n},\;G_{n}$は定数で $v(z,0)$と$\dot{v}(z,0)$の2つの初期条件から決まるが、 $H_{n}=A_{n}F_{n},\;J_{n}=A_{n}G_{n}$と置き直すと
${\displaystyle v(z,t)= \sum_{n=1}^{\infty} \sin(\dfrac{n\pi z}{\ell}) (H_{n}\sin\omega_{n}t+J_{n}\cos\omega_{n}t) }$
となる。 $\omega_{n}$は固有角振動数で、
$\omega_{n}=\left(\dfrac{n\pi}{\ell}\right)^{2}\sqrt{\dfrac{EI}{\rho A}} \;\;\;\;(n=1,2,3,...)$  (単純支持の場合)
となる。 左端固定の片持ばりの場合は、 岩熊哲夫・小山茂『鬆徒労苦衷有迷禍荷苦痛-- 計算機による構造解析の基礎としての構造力学を独習する』 の10.4.3.3 片持ち梁参照。
さて、ここでは、2つの微分方程式
$y''''(z)-\mu^{4}y(z)=0$
$\ddot{a}(t)+\omega_{n}^{2}a(t)=0$
を固有値問題として解いていて、 $\mu^{4}$や$\omega_{n}^{2}$が固有値に対応し、 $y_{n}(z)$や$a_{n}(t)$が固有関数に対応している。 $\omega_{n}$は固有角振動数に対応するし、 $y_{n}(z)$は振動モードに対応する。