
以下の話の流れや導出方法等は、 後藤の恩師の岩熊先生と後輩の小山さんとの共著: 岩熊哲夫・小山茂『鬆徒労苦衷有迷禍荷苦痛-- 計算機による構造解析の基礎としての構造力学を独習する』 の 10. 振動論の基礎 のやり方を参考にしています。 名城大学の村田 賢先生の 多自由度系の自由振動も参考にしました。 まだ、準備開始したばかりなので、間違いとか、それなりにあるかもしれません。 大幅に書き換える可能性もあります。
 1自由度系の自由振動、減衰自由振動、
強制振動などの変位がどう導かれるかがおおよそわかったところで、
多自由度系の変位がどう表せるのかについて考えてみたい。
まずは2自由度系から。
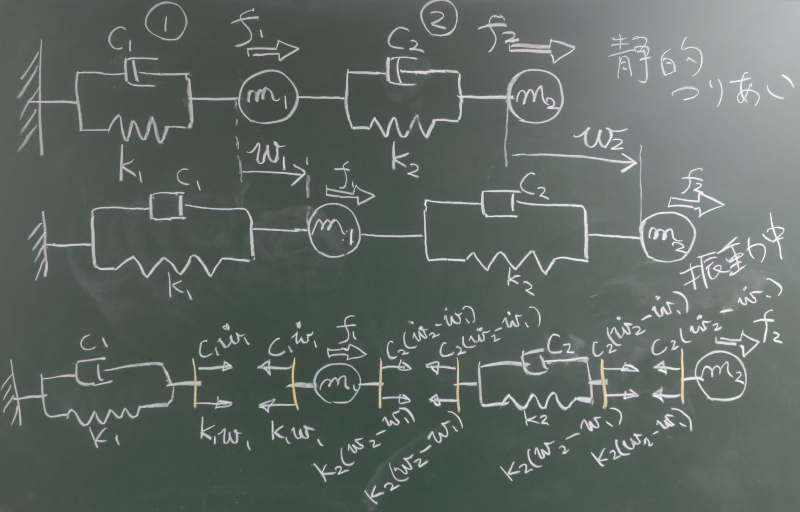
鉛直で考えてると、
自然長を原点とした変位$y$と
静的つりあい位置を原点とした変位$v$が
重力の影響で、
$y=v+\frac{mg}{k}$のようにずれるのがちょっとめんどくさいのと、
ばねがつながっている絵は横向きの方が横書きの文章中に挿入しやすいので、
ここでは、図のように横向きで2自由度系を考える。
ばね定数$k_{1}$のばねと粘性減衰係数$c_{1}$のダッシュポッドが
並列につながれた右端に質点$m_{1}$がついている1自由度振動系①と、
ばね定数$k_{2}$のばねと粘性減衰係数$c_{2}$のダッシュポッドが
並列につながれた右端に質点$m_{2}$がついている1自由度振動系②が
直列に繋がれて2自由度系を形成し、その左端が壁にくっついているものとする。
静的つりあい状態の質点$m_{1}$の位置を基準にした
質点$m_{1}$の右($z$)方向変位を$w_{1}(t)$,
静的つりあい状態の質点$m_{2}$の位置を基準にした
質点$m_{2}$の右($z$)方向変位を$w_{2}(t)$とする。
式中では、適宜$(t)$を省略して$w_{1}, \;w_{2}$と書く。
1自由度系の自由振動、減衰自由振動、
強制振動などの変位がどう導かれるかがおおよそわかったところで、
多自由度系の変位がどう表せるのかについて考えてみたい。
まずは2自由度系から。
鉛直で考えてると、
自然長を原点とした変位$y$と
静的つりあい位置を原点とした変位$v$が
重力の影響で、
$y=v+\frac{mg}{k}$のようにずれるのがちょっとめんどくさいのと、
ばねがつながっている絵は横向きの方が横書きの文章中に挿入しやすいので、
ここでは、図のように横向きで2自由度系を考える。
ばね定数$k_{1}$のばねと粘性減衰係数$c_{1}$のダッシュポッドが
並列につながれた右端に質点$m_{1}$がついている1自由度振動系①と、
ばね定数$k_{2}$のばねと粘性減衰係数$c_{2}$のダッシュポッドが
並列につながれた右端に質点$m_{2}$がついている1自由度振動系②が
直列に繋がれて2自由度系を形成し、その左端が壁にくっついているものとする。
静的つりあい状態の質点$m_{1}$の位置を基準にした
質点$m_{1}$の右($z$)方向変位を$w_{1}(t)$,
静的つりあい状態の質点$m_{2}$の位置を基準にした
質点$m_{2}$の右($z$)方向変位を$w_{2}(t)$とする。
式中では、適宜$(t)$を省略して$w_{1}, \;w_{2}$と書く。
質点$m_{1}$についての運動方程式と
質点$m_{2}$についての運動方程式を考える。
質点$m_{1}$と質点$m_{2}$をそれぞれ振動系から切り離して
質点だけにして、作用している力の合計$\sum\!\!\rightarrow$を考える。
作用している力の少ない質点$m_{2}$の方から考える。
切断面に作用している軸力は、
振動系②のばねの抵抗力とダッシュポッドの抵抗力だけど、
ばねの抵抗力は
振動系②の
(静的つりあいからの)のび(両端の相対変位)に$k_{2}$をかければいいだろうし、
ダッシュポッドの抵抗力は
振動系②の
(静的つりあいからの)のびの速度(振動系②の両端の相対速度)
に$c_{2}$をかければいいだろう。
両端がともに変位する系ののびや相対速度を両端の変位から
どうやって求めればいいかということは、
マトリクス構造解析での考察を
参考にすれば、
のびは$w_{2}-w_{1}$,
両端の相対速度は$\dot{w_{2}}-\dot{w_{1}}$
となるのがわかるだろう。
というわけで、
質点$m_{2}$の運動方程式
$\sum\!\!\rightarrow =m_{2}\ddot{w}_{2}$
は、
$-c_{2}(\dot{w_{2}}-\dot{w_{1}})-k_{2}(w_{2}-w_{1})+f_{2}=m_{2}\ddot{w}_{2}$
となる。
質点$m_{1}$の運動方程式も同様だが、
右の切断面の軸力は、
振動系②のばねの抵抗力とダッシュポッドの抵抗力と考えられるから、
質点$m_{2}$と同じ(ただし、引張正の向きは右向き)。
左の切断面の軸力は、
振動系①のばねの抵抗力とダッシュポッドの抵抗力と考えられるから、
ばねの抵抗力は振動系①の両端の相対変位$w_{1}-0$に$k_{1}$を
かけたもの、
ダッシュポッドの抵抗力は振動系①の両端の相対速度$\dot{w_{1}}-0$に$c_{1}$を
かけたものと考えられる。
よって、質点$m_{1}$の運動方程式
$\sum\!\!\rightarrow =m_{1}\ddot{w}_{1}$
は、
$
-c_{1}\dot{w}_{1}-k_{1}w_{1}
+c_{2}(\dot{w}_{2}-\dot{w}_{1})+k_{2}(w_{2}-w_{1})+f_{1}
=m_{1}\ddot{w}_{1}$
となる。
これら2式を少し整理して書くと
$
\begin{array}{rrrrr}
m_{1}\ddot{w}_{1} &
+(c_{1}+c_{2})\dot{w}_{1} &
-c_{2}\dot{w}_{2} &
+(k_{1}+k_{2})w_{1} &
-k_{2}w_{2}
=
f_{1}
\\
m_{2}\ddot{w}_{2} &
-c_{2}\dot{w}_{1} &
+c_{2}\dot{w}_{2} &
-k_{2}w_{1} &
+k_{2}w_{2}
=
f_{2}
\end{array}
$
となるから、
質量行列$\mathbf{M}$,
減衰行列$\mathbf{C}$,
剛性行列$\mathbf{K}$,
変位ベクトル$\mathbf{w}$,
外力ベクトル$\mathbf{f}$を
以下のように定義すると、
$\mathbf{M}=
\left(
\begin{array}{cc}
m_{1} & 0 \\
0 & m_{2}
\end{array}
\right)
\\
\mathbf{C}=
\left(
\begin{array}{cc}
c_{1}+c_{2} & -c_{2} \\
-c_{2} & c_{2}
\end{array}
\right)
\\
\mathbf{K}=
\left(
\begin{array}{cc}
k_{1}+k_{2} & -k_{2} \\
-k_{2} & k_{2}
\end{array}
\right)
\\
\mathbf{w}=
\left(
\begin{array}{c}
w_{1}\\
w_{2}
\end{array}
\right)
\\
\mathbf{f}=
\left(
\begin{array}{c}
f_{1}\\
f_{2}
\end{array}
\right)
$
質点$m_{1}$と質点$m_{2}$の運動方程式は、まとめて以下のように表せる。
$
\mathbf{M}\ddot{\mathbf{w}}
+\mathbf{C}\dot{\mathbf{w}}
+\mathbf{K}\mathbf{w}
=\mathbf{f}
$
簡単のため、非減衰自由振動の場合を考えてみると、
$\mathbf{C}$と$\mathbf{f}$は考えなくていいので、
運動方程式は以下のように表せる。
$
\mathbf{M}\ddot{\mathbf{w}}
+\mathbf{K}\mathbf{w}
=\mathbf{0}
$
1自由度系の非減衰自由振動の変位は、
$w(t)=A\sin\omega t+B\cos\omega t$
のように表せた。
三角関数の合成を使うと、
$w(t)=A\sin\omega t+B\cos\omega t\\
=C\sin(\omega t + \alpha)$
ただし、
$C=\sqrt{A^{2}+B^{2}},\;\;
\alpha=\dfrac{B}{A}$
質点1と質点2は、同じ角振動数$\omega$で、
位相差もなく(どちらの位相も$\omega t+\alpha$で)振動しているものとする。
人によっては、質点1が
$\omega_{1}=\sqrt{\frac{k_{1}}{m_{1}}}$で、
質点2が
$\omega_{2}=\sqrt{\frac{k_{2}}{m_{2}}}$で、
それぞればらばらに振動したりしないのかと思ったりするかもしれないが、
実際に振動させてみたのを
YouTubeにアップしてみたが、
やや質量の異なる質点2つを、長さの違う(つまり$k$の違う)ばねでつないで
みると、位相はずれずに同じ角振動数で振動しているように見える
(振幅は違うけど)。
質点1と質点2は位相差がないのであれば、
初期位相$\alpha$もない方が式が簡単になるので、
質点1と質点2が振動の中心に来た時刻を$t=0$ということにして、初期位相$\alpha=0$ということにする。
そうすると、質点1の変位$w_{1}$と質点2の変位$w_{2}$は、
以下のように表せる。
$w_{1}=C_{1}\sin\omega t\\
w_{2}=C_{2}\sin\omega t$
$C_{1},\; C_{2}$は質点1と質点2の振幅なので、
振幅ベクトル$\mathbf{c}$を
$\mathbf{c}=
\left(
\begin{array}{c}
C_{1}\\
C_{2}
\end{array}
\right)
$
と定義すると、上の2式は以下のように表せる。
$\mathbf{w}=\mathbf{c}\sin\omega t$
1回微分すると、
$\mathbf{\dot{w}}=\omega\mathbf{c}\cos\omega t$
もう1回微分すると、
$\mathbf{\ddot{w}}=-\omega^{2}\mathbf{c}\sin\omega t$
となるから、
$\mathbf{\ddot{w}}=-\omega^{2}\mathbf{w}$
と表せる。
これを運動方程式
$
\mathbf{M}\ddot{\mathbf{w}}
+\mathbf{K}\mathbf{w}
=\mathbf{0}
$
に代入すると、
$-\omega^{2}\mathbf{M}\mathbf{w}
+\mathbf{K}\mathbf{w}
=\mathbf{0}
$
$
(\mathbf{K}
-\omega^{2}\mathbf{M})\mathbf{w}
=\mathbf{0}
$
$
(\mathbf{K}
-\omega^{2}\mathbf{M})
\mathbf{c}\sin\omega t
=\mathbf{0}
$
と変形できる。
この式が常に成り立つには、
$
(\mathbf{K}
-\omega^{2}\mathbf{M})
\mathbf{c}
=\mathbf{0}
$
でなければならない。この式を成分でちゃんと書くと以下のようになるが、
$
\left(
\left(
\begin{array}{cc}
k_{1}+k_{2} & -k_{2} \\
-k_{2} & k_{2}
\end{array}
\right)
-\omega^{2}
\left(
\begin{array}{cc}
m_{1} & 0 \\
0 & m_{2}
\end{array}
\right)
\right)
\left(
\begin{array}{c}
C_{1}\\
C_{2}
\end{array}
\right)
=
\left(
\begin{array}{c}
0\\
0
\end{array}
\right)
$
固有値解析の式とも似ている
(質量行列の行列の逆行列をかけて、$\omega^{2}$に
単位行列がかけてあるようにすれば)。
$(\mathbf{A}-\lambda\mathbf{E})\mathbf{x}=0$が
なりたつ$\mathbf{0}$以外の$\mathbf{x}$が存在するためには、
$(\mathbf{A}-\lambda\mathbf{E})$の行列式が$0$でなければならないというのは線形代数でやったと思う。
この場合、$\mathbf{c}=\mathbf{0}$は静止して動かない状態だから、
自由振動の解として
ほしいのは、
$
(\mathbf{K}
-\omega^{2}\mathbf{M})
$
の行列式が$\mathbf{0}$になる方の答えだ。
というわけで、以下の行列式を計算してみる。
$
\det\left|
\begin{array}{cc}
(k_{1}+k_{2})-m_{1}\omega^{2} & -k_{2} \\
-k_{2} & k_{2}-m_{2}\omega^{2}
\end{array}
\right|
=0
$
$
((k_{1}+k_{2})-m_{1}\omega^{2})
(k_{2}-m_{2}\omega^{2})
-k_{2}^{2}=0$
これを整理すると、
$m_{1}m_{2}\omega^{4}-(m_{1}k_{2}+m_{2}(k_{1}+k_{2}))\omega^{2}+k_{1}k_{2}=0$
$\omega^{4}
-\left(
\left(\dfrac{k_{2}}{m_{2}}\right)
+\left(\dfrac{k_{1}}{m_{1}}\right)
+\left(\dfrac{m_{2}}{m_{1}}\right)
\left(\dfrac{k_{2}}{m_{2}}\right)
\right)\omega^{2}
+
\left(\dfrac{k_{1}}{m_{1}}\right)
\left(\dfrac{k_{2}}{m_{2}}\right)
=0$
ここで、式を以下のように見やすくするために
$\omega_{1}=\sqrt{\frac{k_{1}}{m_{1}}}, \;
\omega_{2}=\sqrt{\frac{k_{2}}{m_{2}}}$
とおくが、上述したように、
$\omega_{1}$と$\omega_{2}$は質点1と質点2の固有角振動数というわけではなく、
質点1も質点2も同じ固有角振動数$\omega$で振動しているので注意。
$\omega^{4}
-\left(\omega_{2}^{2}+\omega_{1}^{2}+\dfrac{m_{2}}{m_{1}}\omega_{2}^{2}\right)\omega^{2}
+\omega_{1}^{2}\omega_{2}^{2}
=0$
解の公式から
$\omega^{2}
=\dfrac{1}{2}\left(
\left(\omega_{2}^{2}+\omega_{1}^{2}+\dfrac{m_{2}}{m_{1}}\omega_{2}^{2}\right)
\pm\sqrt{
\left(\omega_{2}^{2}+\omega_{1}^{2}+\dfrac{m_{2}}{m_{1}}\omega_{2}^{2}\right)^{2}
-4\omega_{1}^{2}\omega_{2}^{2}
}
\;\;\right)
$
$\omega$は実数なので、
まずは$\sqrt{\;\;}$の中は正である必要があるが、確認してみる。
$
\left(\omega_{2}^{2}+\omega_{1}^{2}+\dfrac{m_{2}}{m_{1}}\omega_{2}^{2}\right)^{2}
-4\omega_{1}^{2}\omega_{2}^{2}\\
=
\left(\omega_{2}^{2}+\omega_{1}^{2}\right)^{2}
+2\left(\omega_{2}^{2}+\omega_{1}^{2}\right)
\dfrac{m_{2}}{m_{1}}\omega_{2}^{2}
+\dfrac{m_{2}^{2}}{m_{1}^{2}}\omega_{2}^{4}
-4\omega_{1}^{2}\omega_{2}^{2}\\
=\left(\omega_{2}^{2}-\omega_{1}^{2}\right)^{2}
+2\left(\omega_{2}^{2}+\omega_{1}^{2}\right)
\dfrac{m_{2}}{m_{1}}\omega_{2}^{2}
+\dfrac{m_{2}^{2}}{m_{1}^{2}}\omega_{2}^{4}
\gt 0
$
ということで、$\sqrt{\;\;}$の中身は正であることはわかったが、
$\left(\omega_{2}^{2}+\omega_{1}^{2}+\dfrac{m_{2}}{m_{1}}\omega_{2}^{2}\right)$
が
$\sqrt{\;\;}$より
大きくないと$\omega$は実数にならない。
両者をそれぞれ2乗すると、
$\left(\omega_{2}^{2}+\omega_{1}^{2}+\dfrac{m_{2}}{m_{1}}\omega_{2}^{2}\right)^{2}$
と
$\left(\omega_{2}^{2}+\omega_{1}^{2}+\dfrac{m_{2}}{m_{1}}\omega_{2}^{2}\right)^{2}
-4\omega_{1}^{2}\omega_{2}^{2}$
となるから右側の方が小さい(ただし、負にはならないことも上で確認済み)。
ということで、
$\omega$はめでたく正の実数解ということになるので、
その解を小さい方から$\omega_{m1},\;\;\omega_{m2}$と書くことにする。
$m1,\;\;m2$とつけたのは、後述する1次モード、2次モードに対応する固有角振動数という
意味合い。
式を見やすくなるために置いた$\omega_{1}=\sqrt{\frac{k_{1}}{m_{1}}}, \;
\omega_{2}=\sqrt{\frac{k_{2}}{m_{2}}}$と区別するため。
さて、
$
\left(
\left(
\begin{array}{cc}
k_{1}+k_{2} & -k_{2} \\
-k_{2} & k_{2}
\end{array}
\right)
-\omega^{2}
\left(
\begin{array}{cc}
m_{1} & 0 \\
0 & m_{2}
\end{array}
\right)
\right)
\left(
\begin{array}{c}
C_{1}\\
C_{2}
\end{array}
\right)
=
\left(
\begin{array}{c}
0\\
0
\end{array}
\right)
$
の式に$\omega_{m1},\;\;\omega_{m2}$を代入して、($0$でない)振幅$C_{1}, \; C_{2}$を求めたいが、
この連立方程式は、2式とも右辺が$0$で1次従属となるので、
連立させても$C_{1}$と$C_{2}$の比率しか求まらない。
2番目の式は、
$-k_{2}C_{1}+(k_{2}-\omega^{2}m_{2})C_{2}=0$
これを変形すると、
$\dfrac{C_{2}}{C_{1}}=\dfrac{k_{2}}{k_{2}-m_{2}\omega^{2}}$
となり、$C_{1}$と$C_{2}$の比率が求まるが、この式に、
2つの解
$\omega_{m1},\;\;\omega_{m2}$を代入したものを
$\dfrac{C_{2}(\omega_{m1})}{C_{1}(\omega_{m1})}=\dfrac{k_{2}}{k_{2}-m_{2}\omega_{m1}^{2}}
$
$\dfrac{C_{2}(\omega_{m2})}{C_{1}(\omega_{m2})}=\dfrac{k_{2}}{k_{2}-m_{2}\omega_{m2}^{2}}
$
みたいに表すことにする。
さて、質点1と質点2の変位は以下のように仮定したから、
$w_{1}=C_{1}\sin\omega t\\
w_{2}=C_{2}\sin\omega t$
$C_{1}$と$C_{2}$の比率を使って表すなら、
$\omega_{m1}$に対応する変位は、
$_{m1}w_{1}=D_{m1}C_{1}(\omega_{m1})\sin\omega_{m1} t\\
_{m1}w_{2}=D_{m1}C_{2}(\omega_{m1})\sin\omega_{m1} t$
$\omega_{m2}$に対応する変位は、
$_{m2}w_{1}=D_{m2}C_{1}(\omega_{m2})\sin\omega_{m2} t\\
_{m2}w_{2}=D_{m2}C_{2}(\omega_{m2})\sin\omega_{m2} t$
みたいに表される。ただし、$D_{m1},\;\;D_{m2}$は未定定数。
これらをまとめた一般解は
$
\left(
\begin{array}{c}
w_{1}\\
w_{2}
\end{array}
\right)
=
D_{m1}
\left(
\begin{array}{c}
C_{1}(\omega_{m1})\\
C_{2}(\omega_{m1})
\end{array}
\right)
\sin\omega_{m1}t
+
D_{m2}
\left(
\begin{array}{c}
C_{1}(\omega_{m2})\\
C_{2}(\omega_{m2})
\end{array}
\right)
\sin\omega_{m2}t
$
みたいに表せる。
この
$
\left(
\begin{array}{c}
C_{1}(\omega_{m1})\\
C_{2}(\omega_{m1})
\end{array}
\right)
$
と
$
\left(
\begin{array}{c}
C_{1}(\omega_{m2})\\
C_{2}(\omega_{m2})
\end{array}
\right)
$
は、それぞれ$\omega_{m1}$と$\omega_{m2}$に対応した固有ベクトルであるが、
質点1と質点2の変位の相対的な位置関係
(というか、自由度が増えてくれば、振動系全体が振動している形)
を表しているもので
固有振動モードと呼ばれる。