構造力学IIオンライン授業用テキスト
第14回オンライン授業
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
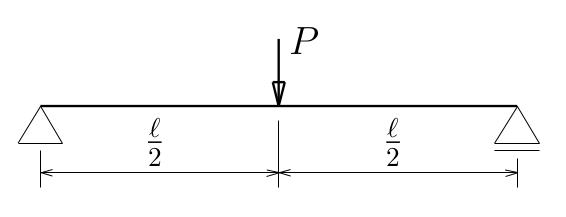第8回で
解いた単純梁の中央の載荷点のたわみを
前回やった
単位荷重法で求めてみよう。
まず、解くべき梁の曲げモーメント分布は、
集中荷重より左側と右側とで場合分けすると、
$
\begin{eqnarray}
M_{左}(z)&=&\frac{P}{2}z \;\;\;\;&(0\le z\le\frac{\ell }{2})\\
M_{右}(z)&=&\frac{P}{2}(\ell -z) \;\;\;\;&(\frac{\ell }{2}\le z\le \ell )
\end{eqnarray}
$
となる。
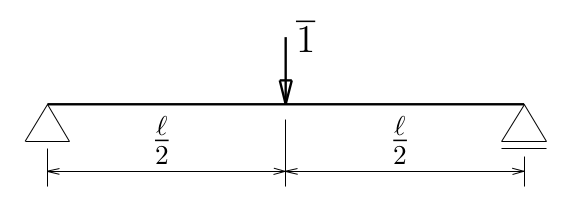たわみを求めたい中央部の鉛直下方向に$\overline{1}$の単位荷重を載荷した
仮想構造の
曲げモーメント分布は、
元の構造の曲げモーメントの$P$に$1$を代入すればいいから、
$
\begin{eqnarray}
\overline{M}_{左}(z)&=&\frac{1}{2}z \;\;\;\;&(0\le z\le\frac{\ell }{2})\\
\overline{M}_{右}(z)&=&\frac{1}{2}(\ell -z) \;\;\;\;&(\frac{\ell }{2}\le z\le \ell )
\end{eqnarray}
$
そうすると、中央の下方向変位$v_{中}$は、
公式から、
$$\overline{1}\cdot v_{中}
=\int_{全部材}\frac{M\overline{M}}{EI}dz$$
を計算すればよい。軸力は作用していないので、曲げモーメントの項だけを
計算すればよい。
$$\overline{1}\cdot v_{中}
=\int_{0}^{\ell }\frac{M(z)\bar{M}(z)}{EI}dz$$
$$=\int_{0}^{\frac{\ell }{2}}\frac{M_{左}(z)\bar{M}_{左}(z)}{EI}dz
+\int_{\frac{\ell }{2}}^{\ell }\frac{M_{右}(z)\bar{M}_{右}(z)}{EI}dz$$
$$=\frac{1}{EI}\int_{0}^{\frac{\ell }{2}}\frac{P}{2}z\cdot \frac{1}{2}zdz
+\frac{1}{EI}\int_{\frac{\ell }{2}}^{\ell }
\frac{P}{2}(\ell -z)\cdot \frac{1}{2}(\ell -z)dz$$
$$=\frac{P}{4EI}\int_{0}^{\frac{\ell }{2}}z^{2}dz
+\frac{P}{4EI}\int_{\frac{\ell }{2}}^{\ell }
(\ell ^{2}-2\ell z+z^{2})dz$$
$$=\frac{P}{4EI}[\frac{z^{3}}{3}]_{0}^{\frac{\ell }{2}}
+\frac{P}{4EI}[\ell ^{2}z-lz^{2}+\frac{z^{3}}{3}]_{\frac{\ell }{2}}^{\ell }$$
$$=\frac{P\ell ^{3}}{48EI}$$
と求まる。
左右対称であるということを利用するなら、$0\le z\le \frac{\ell }{2}$
の左半分の積分だけ求めてそれを2倍するという手もある。
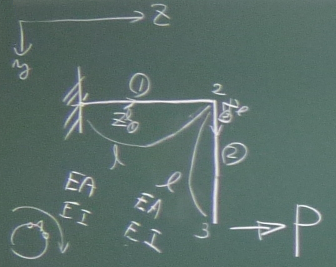単位荷重法で
図のような折れ曲がった片持ち梁（片持ち折れ梁）の
先端の変位（2方向）を求めてみよう。
単位荷重法は、モーメントがすぐに求まる静定ラーメンや
静定折れ梁の載荷点の変位を求めたいときは、重宝する。
まず、図のように部材①，部材②，とし、
長さはともに$\ell$, 伸び剛性はともに$EA$, 曲げ剛性はともに$EI$とする。
節点は、固定端が1, 折れ曲がった点が2, 先端が3とする。
図のように
節点1から部材①にそって局所座標$z_{①}^{\ell}$をとり
（といってもこれは全体座標$z$と同じだが）、
節点2から部材②にそって局所座標$z_{②}^{\ell}$をとる。
これらの座標は、後でそれぞれの軸に沿って積分する際に、
それぞれの軸に沿って積分しているということを
このテキスト上で強調するためだが、
手計算のときは、いちいち添字を書かなくてもいいだろう。
構造力学I第11回で
ラーメンを解いた際に、部材に沿って$z_{A}, z_{B}$といった局所座標を
とったのと同じで、
部材①、部材②の断面力($S$, $N$, $M$)を求める際の座標でもある。
折れ梁やラーメンなど、折れ曲がったものの
断面力($S$, $N$, $M$)を求める際は、
（ラーメンのように下側に囲まれた部分のある構造であれば）
なるべく内側・下側から眺めて、部材に沿って時計回りに座標を取っていく。
もちろん、天井から吊り下げられた構造とか、
囲まれた部分が上側にある場合もあるので、
あくまで目安だが。
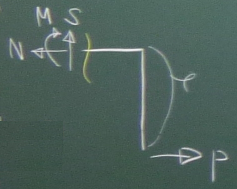まずは、部材①の断面力を求めるため、部材①を任意の点($z_{①}^{\ell}$)で
切り、折れ梁を2つのピースに切り離す。
今回は、（反力を考えなくていい）右側のピースを取り出して力のつりあいを考える。
$z_{①}^{\ell}$は、普通に水平方向なので、
通常の構造力学の向きで断面力($S, N, M$)を切断面に描き入れる。
後は力のつりあいを考える。
$\sum\downarrow=-S=0$ よって$S_{①}=0$
$\sum\rightarrow=-N+P=0$ よって$N_{①}=P$
切断点反時計まわりのモーメントのつりあいを考え
$\sum_{切}\circlearrowleft=-M+P\ell=0$ よって、$M_{①}=P\ell$
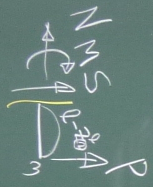次に部材②の断面力を求めるため、部材②を任意の点($z_{②}^{\ell}$)で
切り、折れ梁を2つのピースに切り離す。
今回は、簡単そうな先端側のピースを取り出してつりあいを考える。
断面力($S, N, M$)は、$z_{②}^{\ell}$の関数として求めるのだから、
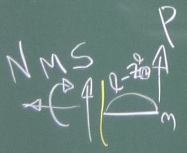$z_{②}^{\ell}$を水平右方向として見ながら、
通常の構造力学の向きで断面力($S, N, M$)を切断面に描き入れる。
後は力のつりあい。
$\sum\downarrow=-S-P=0$ よって$S_{②}=-P$
$\sum\rightarrow=-N=0$ よって$N_{②}=0$
切断点反時計まわりのモーメントのつりあいを考え
$\sum_{切}\circlearrowleft=-M+P(\ell-z_{②}^{\ell})=0$ よって、
$M_{②}=P(\ell-z_{②}^{\ell})$
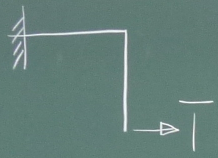まずは簡単な方から。先端の水平右方向変位つまり節点3の$w_{3}$を求める。
変位を求めたい節点の求めたい変位の方向に仮想単位荷重$\overline{1}$を
与える。
計算上は単に荷重として1を与えるだけだが、
「仮想の」荷重であることを強調する際には、適宜、$\overline{1}$みたいに
上バーをつける。
この仮想荷重を与えた仮想構造について、断面力
($\overline{S}, \overline{N}, \overline{M}$)を求める。
といっても、もとの構造の$P$が$1$に変わっただけだから、
上で求めたもとの構造の断面力($S, N, M$)に$P=1$を代入すればよい。
よって、以下のようにこの仮想構造の断面力が求まる。
$\overline{S}_{①}=0$
$\overline{N}_{①}=1$
$\overline{M}_{①}=\ell$
$\overline{S}_{②}=-1$
$\overline{N}_{②}=0$
$\overline{M}_{②}=\ell-z_{②}^{\ell}$
公式から、
$$\overline{1}\cdot w_{3}
=\int_{全部材}\left(
\frac{N\overline{N}}{EA}+\frac{M\overline{M}}{EI}
\right)
dz^{\ell}$$
$z^{\ell}$は部材ごとの軸に沿った局所座標。
十分に細長い梁で、せん断変形の影響は無視しているので、
$\frac{S\overline{S}}{kGA}$みたいなせん断の項は考えない。
すべての部材について、
それぞれの軸に沿って端から端まで
（要は、部材が横たわっている局所系の$z^{\ell}$に沿って）
その部材の長さぶんの積分をすればいい。
つまり、
$$\overline{1}\cdot w_{3}
=\int_{全部材}\left(
\frac{N\overline{N}}{EA}+\frac{M\overline{M}}{EI}
\right)
dz^{\ell}$$
$$=
\int_{0}^{\ell}
\frac{N_{①}\overline{N}_{①}}{EA}dz_{①}^{\ell}
+
\int_{0}^{\ell}
\frac{M_{①}\overline{M}_{①}}{EI}dz_{①}^{\ell}
+
\int_{0}^{\ell}
\frac{N_{②}\overline{N}_{②}}{EA}dz_{②}^{\ell}
+
\int_{0}^{\ell}
\frac{M_{②}\overline{M}_{②}}{EI}dz_{②}^{\ell}
$$
$$=\frac{P\cdot 1\cdot\ell}{EA}+\frac{P\ell\cdot\ell\cdot\ell}{EI}
+\frac{0\cdot 0\cdot\ell}{EA}+
\int_{0}^{\ell}\frac{P(\ell-z_{②}^{\ell})^{2}}{EI}dz_{②}^{\ell}
$$
まず、部材①について、
$N_{①}=P$と$\overline{N}_{①}=1$は定数だから、
$0$から$\ell$までの積分は$\ell$をかけるだけでよい。
$M_{①}=P\ell$と$\overline{M}_{①}=\ell$も定数だから、
この積分も$\ell$をかけるだけ。
次に部材②について、
$N_{②}=0$だし$\overline{N}_{②}=0$だから、積分しても$0$になる。
$M_{②}=P(\ell-z_{②}^{\ell})$と
$\overline{M}_{②}=(\ell-z_{②}^{\ell})$をかけると
$z_{②}^{\ell}$の2次式になるから、これは
$z_{②}^{\ell}$について積分する必要がある。
$z_{②}^{\ell}$の添字を付けたまま積分すると（特に手計算では）
間違いやすいので、以下では、添字をとって、
$z$の積分に書き換える（積分してしまえば同じ答えになるし）。
$$=\frac{P\ell}{EA}+\frac{P\ell^{3}}{EI}+
\frac{P}{EI}\int_{0}^{\ell}
(\ell^{2}-2\ell z+z^{2})dz$$
$$=\frac{P\ell}{EA}+\frac{P\ell^{3}}{EI}+
\frac{P}{EI}\left[\ell^{2}z-\ell z^{2}+\frac{z^{3}}{3}\right]_{0}^{\ell}$$
$$=\frac{P\ell}{EA}+\frac{4P\ell^{3}}{3EI}$$
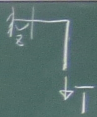では次に、先端の鉛直下方向変位つまり節点3の$v_{3}$を求めてみる。
変位を求めたい節点の求めたい変位の方向に仮想単位荷重$\overline{1}$を
与えて、この仮想構造の断面力
($\overline{S}, \overline{N}, \overline{M}$)を求める。
今度は、もとの構造とは荷重の向きが違うので、
ちゃんと求める必要がある。
まずは部材①について、
任意の点で切り、2つのピースに切り離す。
今回も（反力を考えなくていい）右側のピースを取り出して力のつりあいを考える。
$z_{①}^{\ell}$は$z$と同じだから、切断点から節点2までの距離は、
$\ell-z$で表しておく。
力のつりあいから、以下が求まる。
$\overline{S}_{①}=1$
$\overline{N}_{①}=0$
$\overline{M}_{①}=-(\ell-z)=\ell-z$
次に部材②について、任意の点で切り離し、今回も先端のピースを取り出して
力のつりあいを考える。
力のつりあいから、以下が求まる。
$\overline{S}_{②}=0$
$\overline{N}_{②}=1$
$\overline{M}_{②}=0$
もとの構造の断面力(せん断以外)は、 $N_{①}=P, \; M_{①}=P\ell,\; N_{②}=0, \; M_{②}=P(\ell-z_{②}^{\ell})$だから、公式から以下のように $v_{3}$が求まる。 $$\overline{1}\cdot v_{3} =\int_{全部材}\left( \frac{N\overline{N}}{EA}+\frac{M\overline{M}}{EI} \right) dz^{\ell}$$ $$= \int_{0}^{\ell} \frac{N_{①}\overline{N}_{①}}{EA}dz_{①}^{\ell} + \int_{0}^{\ell} \frac{M_{①}\overline{M}_{①}}{EI}dz_{①}^{\ell} + \int_{0}^{\ell} \frac{N_{②}\overline{N}_{②}}{EA}dz_{②}^{\ell} + \int_{0}^{\ell} \frac{M_{②}\overline{M}_{②}}{EI}dz_{②}^{\ell} $$ $$ = \frac{P\cdot 0\cdot \ell}{EA}+ \int_{0}^{\ell}\frac{P\ell\cdot(z-\ell)}{EI}dz +\frac{0\cdot 1\cdot\ell}{EA} +\int_{0}^{\ell}\frac{P(\ell-z_{②}^{\ell})\cdot 0}{EI}dz_{②}^{\ell} $$ 2項目の部材①の曲げの項以外はすべて0になる $$ =\frac{P\ell}{EI}\left[\frac{z^{2}}{2}-\ell z\right]_{0}^{\ell} =-\frac{P\ell^{3}}{2EI}$$
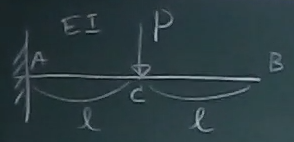図の片持ち梁の先端Bのたわみを単位荷重法で求めよ。
曲げ剛性はEIとする。
答えはここ。
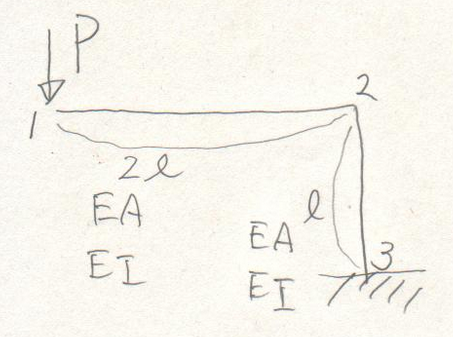図の片持ち折れ梁の節点1の下方向変位$v_{1}$と
右方向変位$w_{1}$を単位荷重法で求めよ。
各部材の曲げ剛性は$EI$, 伸び剛性は$EA$とする。
答えはここ。
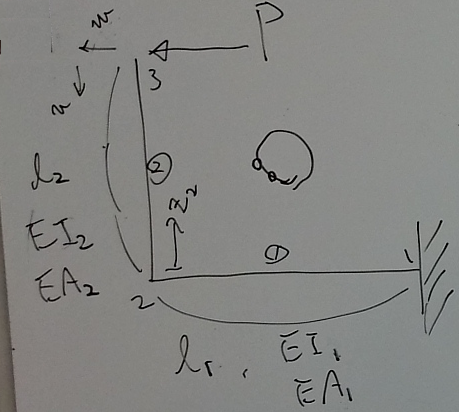梁の長さや剛性が部材①と部材②で違う場合。
節点3の左方向変位
$w_{3}$については、
ここに答え。
ただし、上側から眺めて時計回りに座標をとっている。
研究室のゼミのときになぐり書きしたものだが、
下付き添字に$\ell_{2}$とついているものを
$\ell_{2}^{2}$と2乗したりすると、手計算ではとても間違いやすい。
現に、この計算は最初は間違っていたので、
後から、添字を画像編集して修正している。
2022年度小テスト：
小テスト230201
2021年度小テスト：
問,
解答
2020年度小テスト：
問1-2,
解答
メモ:
