
構造力学(基礎)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
 ラーメン(Rahmen)というのは、
ドイツ語で額縁とか骨組という意味で、
構造分野でも節点が剛結された骨組の意味で用いる。
ちなみに、節点がヒンジで結合された骨組は
トラスであるが、
第3回で説明したように、
現在のトラスは節点(格点)が剛結されているため、
ラーメンの定義を剛結骨組としてしまうと、剛結トラスもラーメンという
ことになってしまう。
が、一般的な世の中の言葉の使われ方としては、
トラス作用を想定して部材を三角形に配置した骨組のことを
(節点が剛結でも)トラスと言い、
剛結された節点が回転を拘束することを想定して
主に縦方向と横方向の
部材からなる四角い枠で構成した骨組のことを
ラーメンと言うと捉えておけばいいのではないかと思う。
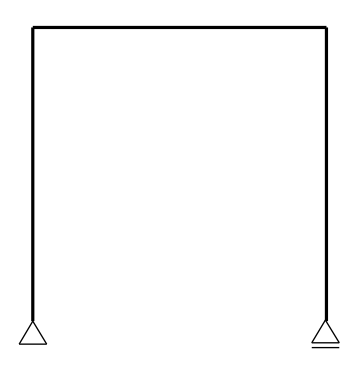
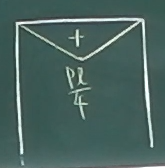
トラスの中でも、図のようなコの字(開いてるところが地面とくっついてる)の
形をしたラーメンを門型ラーメンというが、
単にラーメンという場合は、(土木では)門型ラーメンを指すことが多い。
ラーメン(Rahmen)というのは、
ドイツ語で額縁とか骨組という意味で、
構造分野でも節点が剛結された骨組の意味で用いる。
ちなみに、節点がヒンジで結合された骨組は
トラスであるが、
第3回で説明したように、
現在のトラスは節点(格点)が剛結されているため、
ラーメンの定義を剛結骨組としてしまうと、剛結トラスもラーメンという
ことになってしまう。
が、一般的な世の中の言葉の使われ方としては、
トラス作用を想定して部材を三角形に配置した骨組のことを
(節点が剛結でも)トラスと言い、
剛結された節点が回転を拘束することを想定して
主に縦方向と横方向の
部材からなる四角い枠で構成した骨組のことを
ラーメンと言うと捉えておけばいいのではないかと思う。
トラスの中でも、図のようなコの字(開いてるところが地面とくっついてる)の
形をしたラーメンを門型ラーメンというが、
単にラーメンという場合は、(土木では)門型ラーメンを指すことが多い。
脱線:
昔、ある先生が(たぶん)冗談で、
ラーメンというのは、ラーメンどんぶりを逆さにしたような形をしているから、
ラーメンというんですと言ったのを真に受けて、
信じ続けていた学生がいたが、
確かに、
方杖ラーメンとかは、ラーメンどんぶりをひっくり返したような
形をしているかもしれない。
ラーメンの支点部が単純支持されていて、
力のつりあいで反力や断面力が求まるラーメンのことを静定ラーメンという。
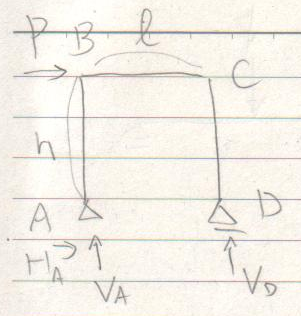
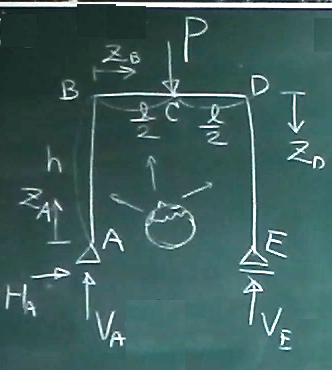 では、図のように静定ラーメンの水平部材の中央に集中荷重を受ける問題を解いてみる。
では、図のように静定ラーメンの水平部材の中央に集中荷重を受ける問題を解いてみる。
反力は、静定なので
第2回でやったように、力のつりあいで
求まる。
左右対称だから、上向きに$\frac{P}{2}$ずつだけど、一応、求める。
$\sum\downarrow=-V_{A}+P-V_{E}=0$
$\sum\rightarrow=H_{A}=0$ つまり、水平反力はない。
$\sum_{A}\circlearrowleft=-P\cdot\frac{\ell}{2}+V_{E}\ell=0$ よって、
$V_{E}=\frac{P}{2}$となり、これを上の式に代入して$V_{A}=\frac{P}{2}$
と求まる。
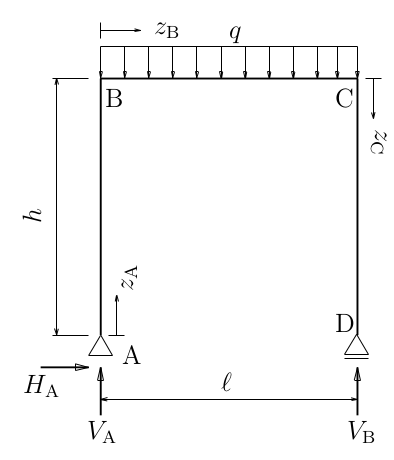
断面力($N(z), S(z), M(z)$)は、梁の場合は、$z$座標の関数だったが、
ラーメンのように複数の直線部材が角度をつけてつながれている場合は、
それぞれの部材に沿って局所座標をとり、それぞれの局所座標ごとに断面力を
求めていく。
通常の門型ラーメンの場合、
ラーメンの内側から見て、左下(点A)から時計回りに局所座標を取っていく。
つまり、まず部材ABについては、点Aを原点としB方向に$z_{A}$をとり、
部材BDについては、点Bを原点としてD方向に$z_{B}$をとり、
部材DEについては、点Dを原点としてE方向に$z_{D}$をとる。
張り出し梁の場合は、
梁の左端を原点とする$z$の関数として、梁全体の断面力を表したが、
ラーメンの場合は、直線部材ごとにその始点を原点に取り直した方が
わかりやすいし、シンプルに表現できる。
ラーメンでは、断面力図を描けることが重要なので、
断面力関数自体は、簡単に表現できる方法を使うのがいいと思う。
内側から見て左側の部材から順番に、 それぞれの局所座標を水平右方向に見て、その断面力を求める。
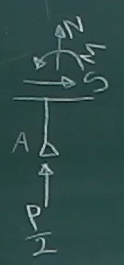 部材ABの断面力を求めるには、部材ABの任意点を切断して
力のつりあいを考えればよい。
部材ABは途中に集中外力が作用していないので、
場合分けは不要である。
なので、AB区間の任意点を切断してラーメンを2つのピースに切り離し、
今回は、左下の(支点A側の)ピースを取り出してつりあいを考える。
部材ABの断面力を求めるには、部材ABの任意点を切断して
力のつりあいを考えればよい。
部材ABは途中に集中外力が作用していないので、
場合分けは不要である。
なので、AB区間の任意点を切断してラーメンを2つのピースに切り離し、
今回は、左下の(支点A側の)ピースを取り出してつりあいを考える。
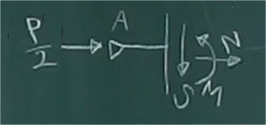 取り出したピースを局所座標$z_{A}$が水平になる方向に見て、
切断面に断面力($N(z_{A}), S(z_{A}), M(z_{A})$)を描き込む。
断面力の向きは、
局所座標$z_{A}$を梁の軸$z$と考えた場合の梁の断面力の向きで描くこと。
力のつりあいから断面力を求める。
以下、$z_{A}$方向を水平右方向として、矢印
($\sum\rightarrow$とか$\sum\downarrow$)
を描いている。
取り出したピースを局所座標$z_{A}$が水平になる方向に見て、
切断面に断面力($N(z_{A}), S(z_{A}), M(z_{A})$)を描き込む。
断面力の向きは、
局所座標$z_{A}$を梁の軸$z$と考えた場合の梁の断面力の向きで描くこと。
力のつりあいから断面力を求める。
以下、$z_{A}$方向を水平右方向として、矢印
($\sum\rightarrow$とか$\sum\downarrow$)
を描いている。
$\sum\rightarrow=\frac{P}{2}+N=0$ よって、
$N(z_{A})=-\frac{P}{2}\;\;\;\;\;(0 \le z_{A}\le h)$
$\sum\downarrow=S=0$ よって、
$S(z_{A})=0\;\;\;\;\;(0 \le z_{A}\le h)$
$\sum_{z_{A}}\circlearrowleft=M=0$ よって、
$M(z_{A})=0\;\;\;\;\;(0 \le z_{A}\le h)$
 部材BDは途中の点Cに集中外力があるので、区間BCと区間CDで場合分けする
必要がある。
部材BDは途中の点Cに集中外力があるので、区間BCと区間CDで場合分けする
必要がある。
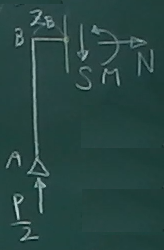 区間BCの断面力を求めるには、区間BCの任意点$z_{B}$を切断して
ラーメンを2つのピースに切り離し、
そのどちらかのピースを取り出して 力のつりあいを考えればよい。
今回は、左側(点B側)のピースを取り出す。
$z_{B}$は、もともと水平だから、普通の梁と同様に断面力を描き込んで、
普通に力のつりあいを考える。
区間BCの断面力を求めるには、区間BCの任意点$z_{B}$を切断して
ラーメンを2つのピースに切り離し、
そのどちらかのピースを取り出して 力のつりあいを考えればよい。
今回は、左側(点B側)のピースを取り出す。
$z_{B}$は、もともと水平だから、普通の梁と同様に断面力を描き込んで、
普通に力のつりあいを考える。
$\sum\rightarrow=N=0$ よって、
$N(z_{B})=0\;\;\;\;\;
(0 \le z_{B}\le \frac{\ell}{2})$
$\sum\downarrow=-\frac{P}{2}+S=0$ よって、
$S(z_{B})=\frac{P}{2}\;\;\;\;\;
(0 \le z_{B}\le \frac{\ell}{2})$
$\sum_{z_{B}}\circlearrowleft=-\frac{P}{2}\cdot z_{B}+M=0$ よって、
$M(z_{B})=\frac{P}{2}z_{B}\;\;\;\;\;
(0 \le z_{B}\le \frac{\ell}{2})$
反力$\frac{P}{2}$の切断点($z_{B}$点)回りの
モーメントの腕の長さは、点B($z_{B}=0$)
から切断点($z_{B}=z_{B}$点)までの距離だから、
$z_{B}$でよい。
 区間CDの断面力を求めるには、区間CDの任意点$z_{B}$を切断して
ラーメンを2つのピースに切り離し、
そのどちらかのピースを取り出して 力のつりあいを考えればよい。
今回は、右側(点D側)のピースを取り出す。
$z_{B}$は、もともと水平だから、普通の梁と同様に断面力を描き込んで、
普通に力のつりあいを考える。
区間CDの断面力を求めるには、区間CDの任意点$z_{B}$を切断して
ラーメンを2つのピースに切り離し、
そのどちらかのピースを取り出して 力のつりあいを考えればよい。
今回は、右側(点D側)のピースを取り出す。
$z_{B}$は、もともと水平だから、普通の梁と同様に断面力を描き込んで、
普通に力のつりあいを考える。
$\sum\rightarrow=-N=0$ よって、
$N(z_{B})=0\;\;\;\;\;
(\frac{\ell}{2}\le z_{B}\le\ell)$
$\sum\downarrow=-S-\frac{P}{2}=0$ よって、
$S(z_{B})=-\frac{P}{2}\;\;\;\;\;
(\frac{\ell}{2}\le z_{B}\le\ell)$
$\sum_{z_{B}}\circlearrowleft=-M+\frac{P}{2}\cdot (\ell-z_{B})=0$ よって、
$M(z_{B})=\frac{P}{2}(\ell-z_{B})\;\;\;\;\;
(\frac{\ell}{2}\le z_{B}\le\ell)$
反力$\frac{P}{2}$の切断点($z_{B}$点)回りの
モーメントの腕の長さは、
「部材BDの長さ$\ell$」から、
「点B($z_{B}=0$)から切断点($z_{B}=z_{B}$点)までの距離$z_{B}$」を
引いたものだから、
$\ell-z_{B}$となる。
これは、梁で右側ピースを取り出して考える場合と同様である。
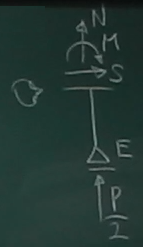 部材DEの断面力を求めるには、部材DEの任意点を切断して
力のつりあいを考えればよい。
部材DEは途中に集中外力が作用していないので、
場合分けは不要である。
なので、DE区間の任意点を切断してラーメンを2つのピースに切り離し、
今回は、右下の(支点E側の)ピースを取り出してつりあいを考える。
部材DEの断面力を求めるには、部材DEの任意点を切断して
力のつりあいを考えればよい。
部材DEは途中に集中外力が作用していないので、
場合分けは不要である。
なので、DE区間の任意点を切断してラーメンを2つのピースに切り離し、
今回は、右下の(支点E側の)ピースを取り出してつりあいを考える。
 取り出したピースを局所座標$z_{D}$が水平になる方向に見て、
切断面に断面力($N(z_{D}), S(z_{D}), M(z_{D})$)を描き込む。
断面力の向きは、
局所座標$z_{D}$を梁の軸$z$と考えた場合の梁の断面力の向きで描くこと。
力のつりあいから断面力を求める。
以下、$z_{D}$方向を水平右方向として、矢印
($\sum\rightarrow$とか$\sum\downarrow$)
を描いている。
取り出したピースを局所座標$z_{D}$が水平になる方向に見て、
切断面に断面力($N(z_{D}), S(z_{D}), M(z_{D})$)を描き込む。
断面力の向きは、
局所座標$z_{D}$を梁の軸$z$と考えた場合の梁の断面力の向きで描くこと。
力のつりあいから断面力を求める。
以下、$z_{D}$方向を水平右方向として、矢印
($\sum\rightarrow$とか$\sum\downarrow$)
を描いている。
$\sum\rightarrow=-N-\frac{P}{2}=0$ よって、
$N(z_{D})=-\frac{P}{2}\;\;\;\;\;(0 \le z_{D}\le h)$
$\sum\downarrow=-S=0$ よって、
$S(z_{D})=0\;\;\;\;\;(0 \le z_{D}\le h)$
$\sum_{z_{D}}\circlearrowleft=-M=0$ よって、
$M(z_{D})=0\;\;\;\;\;(0 \le z_{D}\le h)$
以上、局所座標ごとに求めた断面力を整理する。
$
N(z_{A})=-\frac{P}{2} \;\;\;\;(0\le z_{A} \le h)\\
N(z_{B})=0 \;\;\;\;(0\le z_{B} \le \ell)\\
N(z_{D})=-\frac{P}{2} \;\;\;\;(0\le z_{D} \le h)\\
\ \\
$
$
S(z_{A})=0 \;\;\;\;(0\le z_{A} \le h)\\
S(z_{B})=
\begin{cases}
\frac{P}{2} & \;\;\;\;(0\le z_{B} \le \frac{\ell}{2})\\
-\frac{P}{2} & \;\;\;\;(\frac{\ell}{2}\le z_{B} \le \ell)\\
\end{cases}
\ \\
S(z_{D})=0 \;\;\;\;(0 \le z_{D} \le h)\\
\ \\
$
$
M(z_{A})=0 \;\;\;\;(0\le z_{A} \le h)\\
M(z_{B})=
\begin{cases}
\frac{P}{2}z_{B} & \;\;\;\;(0\le z_{B} \le \frac{\ell}{2})\\
\frac{P}{2}(\ell-z_{B}) & \;\;\;\;(\frac{\ell}{2}\le z_{B} \le \ell)\\
\end{cases}
\ \\
M(z_{D})=0 \;\;\;\;(0 \le z_{D} \le h)\\
\ \\
$
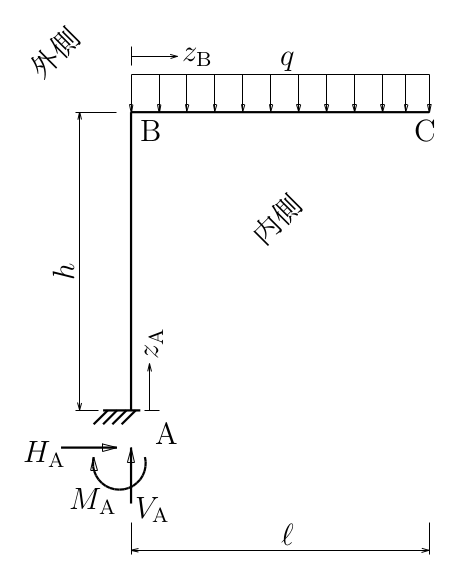
断面力図の軸の正負は、梁の場合は、 この授業では、 第6回目で、 N図は上が正、S図は上が正、M図は下が正、 と決めた。 ラーメンについても、同様に、各局所座標を水平右方向に見た場合に、 N図は上が正、S図は上が正、M図は下が正、 となるように描くことにする。 つまり、 内側から見て、 N図は外側が正、S図は外側が正、M図は内側が正、 と考えてもよい。 上のように、 $N, S, M$を局所座標の関数として、それぞれの 領域ごとに場合分けして書くとめんどくさいので、 以下のように区間ごとに$N_{AB}$みたいに書いてもいいだろう。
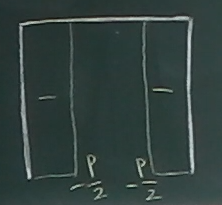 $
N_{AB}=-\frac{P}{2}\\
N_{BC}=0\\
N_{DE}=-\frac{P}{2}\\
$
$
N_{AB}=-\frac{P}{2}\\
N_{BC}=0\\
N_{DE}=-\frac{P}{2}\\
$
$N_{AB}$と$N_{DE}$は
マイナスなので、ラーメンの内側に描く。
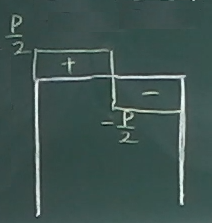 $
S_{AB}=0\\
S_{BC}=
\frac{P}{2}\\
S_{CD}=-\frac{P}{2}\\
S_{DE}=0\\
$
$
S_{AB}=0\\
S_{BC}=
\frac{P}{2}\\
S_{CD}=-\frac{P}{2}\\
S_{DE}=0\\
$
区間BDにしかゼロでない値がないが、
区間BDは、もともと水平なので、梁と同様に描けばよい。
 $
M_{AB}=0\\
M_{BC}=
\frac{P}{2}z_{B}\\
M_{CD}=
\frac{P}{2}(\ell-z_{B})\\
M_{DE}=0\\
$
$
M_{AB}=0\\
M_{BC}=
\frac{P}{2}z_{B}\\
M_{CD}=
\frac{P}{2}(\ell-z_{B})\\
M_{DE}=0\\
$
区間BDにしかゼロでない値がないが、
区間BDは、もともと水平なので、梁と同様に描けばよい。
 図のラーメンについて、
$N$図(外側が正)、
$S$図(外側が正)、$M$図(内側が正)を描け。
答えは、
ここ。
動画の解説は、
第11回その2
の後半にちょっとあるが、
途中で録画が切れてしまっているので、あしからず。
図のラーメンについて、
$N$図(外側が正)、
$S$図(外側が正)、$M$図(内側が正)を描け。
答えは、
ここ。
動画の解説は、
第11回その2
の後半にちょっとあるが、
途中で録画が切れてしまっているので、あしからず。
 構造力学I定期試験(2013年度)から。
答えは、ここ。
作図・計算過程の解答はありません。あしからず。
構造力学I定期試験(2013年度)から。
答えは、ここ。
作図・計算過程の解答はありません。あしからず。
 図のように、途中で折れ曲がっている梁を、折れ梁と言ったりする。
この呼び方はそれほど重要ではないが、この授業では便宜上、折れ梁と呼んでおく。
図のような直線部材2部材の折れ梁だと、3部材のラーメンよりは、
工程が1部材ぶんだけ減るので、やや解く時間が短くなる。
ということで、試験には出しやすい。
支点は1箇所だが、固定端なので片持ち梁と同様に、
モーメント反力が発生する。
構造力学I定期試験(2015年度)から。
$N$図(外側が正)、
$S$図(外側が正)、$M$図(内側が正)を描け。
答えは、ここ。
作図・計算過程の解答はありません。あしからず。
図のように、途中で折れ曲がっている梁を、折れ梁と言ったりする。
この呼び方はそれほど重要ではないが、この授業では便宜上、折れ梁と呼んでおく。
図のような直線部材2部材の折れ梁だと、3部材のラーメンよりは、
工程が1部材ぶんだけ減るので、やや解く時間が短くなる。
ということで、試験には出しやすい。
支点は1箇所だが、固定端なので片持ち梁と同様に、
モーメント反力が発生する。
構造力学I定期試験(2015年度)から。
$N$図(外側が正)、
$S$図(外側が正)、$M$図(内側が正)を描け。
答えは、ここ。
作図・計算過程の解答はありません。あしからず。
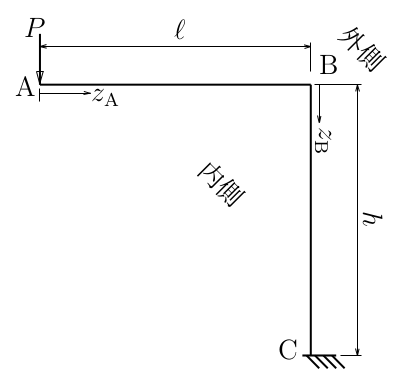 構造力学I定期試験(2018年度)から。
$N$図(外側が正)、
$S$図(外側が正)、$M$図(内側が正)を描け。
答えは、ここ。
作図・計算過程の解答はありません。あしからず。
構造力学I定期試験(2018年度)から。
$N$図(外側が正)、
$S$図(外側が正)、$M$図(内側が正)を描け。
答えは、ここ。
作図・計算過程の解答はありません。あしからず。
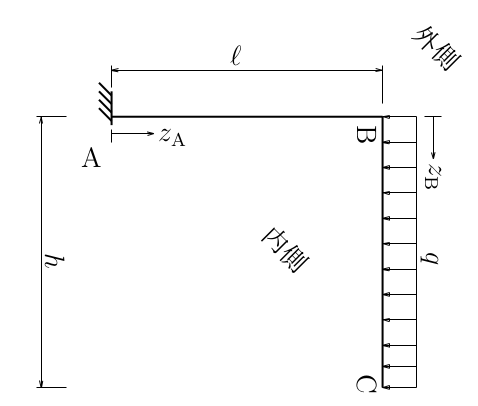 構造力学I定期試験(2019年度)から。
$N$図(外側が正)、
$S$図(外側が正)、$M$図(内側が正)を描け。
答えは、ここ。
構造力学I定期試験(2019年度)から。
$N$図(外側が正)、
$S$図(外側が正)、$M$図(内側が正)を描け。
答えは、ここ。
2024年度小テスト:
小テスト240705
2020年度小テスト:
問1,
問2,
問3,
問4,
解答
メモ: