マトリクス構造解析オンライン授業用テキスト
第14回オンライン授業
オンライン用テキストの準備中：8/12(水)までに用意します。 小さい字は補足説明なので、読み飛ばしてもいいです。
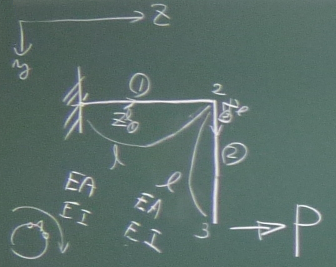第8回で、
片持ち折れ梁を単位荷重法で解いたが、今回は、
これをプログラムで解いてみたい。
単位荷重法で求めた載荷点の変位は、
$v_{3}
=-\frac{P\ell^{3}}{2EI}$
$w_{3}=\frac{P\ell}{EA}+\frac{4P\ell^{3}}{3EI}$
で、断面力は、
$S_{①}=0$
$N_{①}=P$
$M_{①}=P\ell$
$S_{②}=-P$
$N_{②}=0$
$M_{②}=P(\ell-z_{②}^{\ell})$ 部材端での値は、
$M_{②}(0)=P\ell, \;M_{②}(\ell)=0$
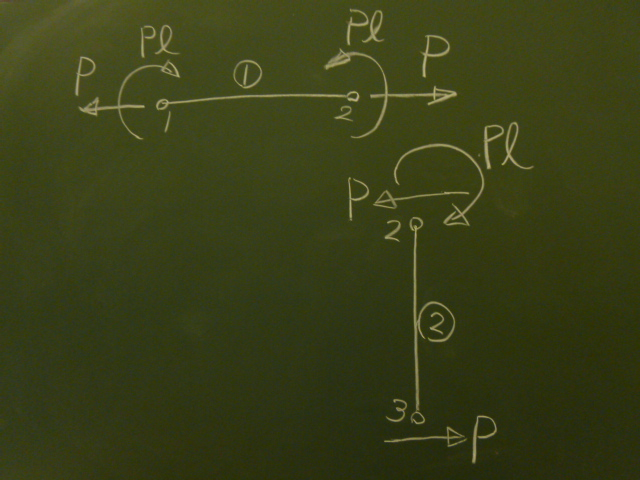部材①、②を切り離して、各節点での断面力の値を、
正の値で描ける向きに矢印を向けて描くと図のようになる。
つまり、各節点の節点力として$y, z$方向、$x$軸右ねじ方向プラスで書くと
以下のようになる。
全体系での節点力なので、
$y$方向であれば軸力だろうがせん断力だろうが$S$となり、
$z$方向であれば軸力だろうがせん断力だろうが$N$となることに注意すると、
以下のようになる。
$S_{1}^{①}=0$
$N_{1}^{①}=-P$
$M_{1}^{①}=-P\ell$
$S_{2}^{①}=0$
$N_{2}^{①}=P$
$M_{2}^{①}=P\ell$
$S_{2}^{②}=0$
$N_{2}^{②}=-P$
$M_{2}^{②}=-P\ell$
$S_{3}^{②}=0$
$N_{3}^{②}=P$
$M_{3}^{②}=0$
となる。
では、 梁の剛性方程式を用いた 骨組のプログラムを使って、上の折れ梁を解いてみよう。 前回のプログラム(hone2sj.f90)を 使って、上のトラスを解いてみよう。 まず、 以下のプログラムをC:\TDM-GCC-64 の中にダウンロードする。 使い方は、torasu2.f90とほぼ同じだが、一応、説明する。
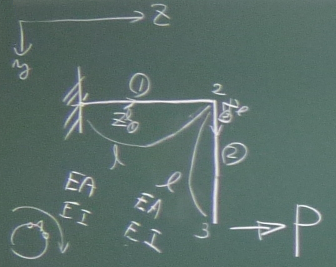今回は、要素数は2要素、節点数は3節点。
pi=asin(1.d0)*2.d0 ! nyou=2 !要素数 nset=3 !節点数
まず、以下のように書いてあるところを見つける。
! 例題1 ! 要素1の剛性マトリクス el=1000.d0 !1本のL(mm) ea=10.d3*10.d0**2 !EA(N) ei=10.d3*10.d0**4/12.d0 !EI(N/mm^2・mm^4) s(1,2,2)= ea/el ; s(1,2,5)= -ea/el s(1,5,2)= -ea/el ; s(1,5,5)= ea/el s(1,1,1)= 12.d0*ei/el**3; s(1,1,3)= -6.d0*ei/el**2 s(1,1,4)=-12.d0*ei/el**3; s(1,1,6)= -6.d0*ei/el**2 s(1,3,1)= -6.d0*ei/el**2; s(1,3,3)= 4.d0*ei/el s(1,3,4)= 6.d0*ei/el**2; s(1,3,6)= 2.d0*ei/el s(1,4,1)=-12.d0*ei/el**3; s(1,4,3)= 6.d0*ei/el**2 s(1,4,4)= 12.d0*ei/el**3; s(1,4,6)= 6.d0*ei/el**2 s(1,6,1)= -6.d0*ei/el**2; s(1,6,3)= 2.d0*ei/el s(1,6,4)= 6.d0*ei/el**2; s(1,6,6)= 4.d0*ei/el
torasu2.f90と同様に、 要素nの要素剛性マトリクス$k_{ij}$が、s(n,i,j)として 与えられている。 これに第7回でやった軸力ありの梁の剛性方程式を入れてやればよい。 上記の要素①については、既に、$6\times 6$のマトリクスの成分が、 ea($EA$), el($\ell$), ei($EI$)などの変数で与えられているから、 あとは、ea, el, eiを適切に与えてやればよい。 マトリクスは初期化しているので、0の成分は与えなくてもよい。 今回は、第12回でやったのと同様に、 計算を確かめるために、$EA=1, EI=1, \ell=1$を与えて計算する。 つまり、el, ea, eiのところをすべて1.d0に書き換えればよい。 または、下記のように 直後の行で定義し直せばよい。
el=1000.d0 !1本のL(mm) ea=10.d3*10.d0**2 !EA(N) ei=10.d3*10.d0**4/12.d0 !EI(N/mm^2・mm^4) el=1.d0 ea=1.d0 ei=1.d0
次にその下の要素②以降のマトリクスを定義する。
! 要素2~4の剛性マトリクス do k=2,4 do i=1,6 do j=1,6 s(k,i,j)=s(1,i,j) end do end do end do
上の例は、要素②から要素④までに要素①と同じs(1,i,j) つまり$k_{ij}^{①}$を与えている。 今回は、要素②までしかなく、要素②は、要素①と同じ要素でいいから、 一番外側のdo k=2, 4（要素②から④まで）のループは削除して、 s(2,i,j) つまり$k_{ij}^{②}$に要素①の剛性マトリクスを代入すればよい。つまり、
! 要素2の剛性マトリクス do i=1,6 do j=1,6 s(2,i,j)=s(1,i,j) end do end do
要素5の剛性マトリクスは、使わないので削除する。または ! を入れてコメントにする。
! 要素5の剛性マトリクス !el=1000.d0*sqrt(2.d0) !1本のL(mm) !s(5,2,2)= ea/el ; s(5,2,5)= -ea/el !s(5,5,2)= -ea/el ; s(5,5,5)= ea/el !s(5,1,1)= 12.d0*ei/el**3; s(5,1,3)= -6.d0*ei/el**2 !s(5,1,4)=-12.d0*ei/el**3; s(5,1,6)= -6.d0*ei/el**2 !s(5,3,1)= -6.d0*ei/el**2; s(5,3,3)= 4.d0*ei/el !s(5,3,4)= 6.d0*ei/el**2; s(5,3,6)= 2.d0*ei/el !s(5,4,1)=-12.d0*ei/el**3; s(5,4,3)= 6.d0*ei/el**2 !s(5,4,4)= 12.d0*ei/el**3; s(5,4,6)= 6.d0*ei/el**2 !s(5,6,1)= -6.d0*ei/el**2; s(5,6,3)= 2.d0*ei/el
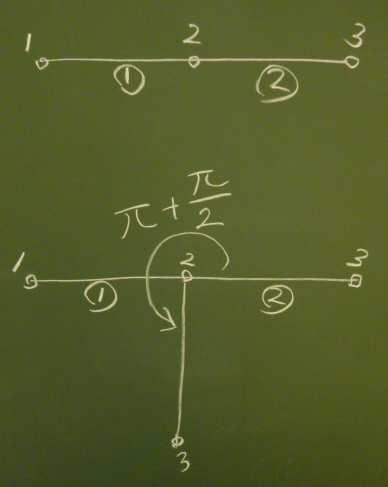今回の要素は、初期状態で$z$軸に左から要素①、②、節点1, 2, 3の
順で並べられるから、
この状態での各要素の左節点番号(idari)と右節点番号(migi)を与える。
要素③以降は、削除するか ! を入れてコメントにする。
idari(1)=1; migi(1)=2 idari(2)=2; migi(2)=3 ! idari(3)=3; migi(3)=4 ! idari(4)=1; migi(4)=4 ! idari(5)=1; migi(5)=3
次に各要素の回転角を、初期状態での左節点を中心に反時計回りの回転角で与える。 $yz$平面の回転角は、$x$軸右ねじ回転なので、反時計回りになる。 要素①は初期状態から動かないのでth(1)=0. 要素②は、$\pi+\frac{\pi}{2}$だけ 回転させればよい。 要素③以降はないので、削除するか、! を入れてコメントにする。
!各要素の回転角（上の左右節点番号がz軸に横たわる状態からの） th(1)=0.d0 th(2)=pi+pi/2.d0 ! th(3)=pi ! th(4)=pi+pi/2.d0 ! th(5)=pi/4.d0
次は境界条件である。 回転角の下の以下のように書いてあるところを見つける。
!境界条件 xv(4)=0.d0!; xw(4)=0.d0; xt(4)=0.d0 xv(3)=0.d0; xw(3)=0.d0!; xt(3)=0.d0
()内は拘束する節点番号、xvは$v$, xwは$w$, xtは$\theta$を意味する。 今回は、節点1で、$v_{1}=w_{1}=\theta_{1}=0$だから、 以下のように与える。 ; で並べて書いたり、! でコメントにしたりすると間違いやすいので、 1行に1つの式ずつ書いた方が安全かもしれない。
!境界条件 xv(1)=0.d0 xw(1)=0.d0 xt(1)=0.d0
境界条件の下の 以下のように書いてあるとこを見つける。
!載荷条件 !cx(2)=1.d0 ! 例題1 fz(2)=200!N
()内は、荷重を与える節点番号。 fyは$y$方向荷重、fzは$z$方向荷重、cxは$x$軸右ねじ回りのモーメント荷重を与える。 今回は、節点3の$z$方向に$P=1$を与えたいので、以下のようにする。
!載荷条件 !cx(2)=1.d0 ! 例題1 fz(3)=1.d0
プログラムの修正が終わったら、 修正したプログラムは、例えば"hone2sj2.f90"みたいに名前を変えて保存する。 プログラムをコンパイルして実行すると、 画像のような画面が表示される。
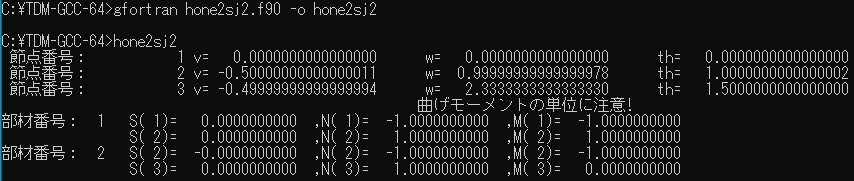
単位荷重法では、
$v_{3}
=-\frac{P\ell^{3}}{2EI}$
$w_{3}=\frac{P\ell}{EA}+\frac{4P\ell^{3}}{3EI}$
だから、$P=1, \ell=1, EI=1, EA=1$を代入すると、
$v_{3}=-\frac{1}{2}=-0.5$
$w_{3}=1+\frac{4}{3}=2.333333....$
であるから、節点番号3のところを見ると、ほぼ合っている。
節点番号： 3 v= -0.49999999999999994 w= 2.3333333333333330 th= 1.5000000000000000
節点力は、$P=1, \ell=1$とすると、
$S_{1}^{①}=0$
$N_{1}^{①}=-P=-1$
$M_{1}^{①}=-P\ell=-1$
$S_{2}^{①}=0$
$N_{2}^{①}=P=1$
$M_{2}^{①}=P\ell=1$
$S_{2}^{②}=0$
$N_{2}^{②}=-P=-1$
$M_{2}^{②}=-P\ell=-1$
$S_{3}^{②}=0$
$N_{3}^{②}=P=1$
$M_{3}^{②}=0$
だから、これも合ってそうだ。
部材番号： 1 S( 1)= 0.0000000000 ,N( 1)= -1.0000000000 ,M( 1)= -1.0000000000
S( 2)= 0.0000000000 ,N( 2)= 1.0000000000 ,M( 2)= 1.0000000000
部材番号： 2 S( 2)= -0.0000000000 ,N( 2)= -1.0000000000 ,M( 2)= -1.0000000000
S( 3)= 0.0000000000 ,N( 3)= 1.0000000000 ,M( 3)= 0.0000000000
以下の片持ち折れ梁（自分の学籍番号のもの）の 載荷点の節点変位($v, w$)を単位荷重法で求めよ。 部材の長さ、伸び剛性、曲げ剛性は2部材ともそれぞれ$\ell$, $EA$, $EI$とする。 次に、$P=E=A=\ell=1.$として、 それをhone2sj.f90で解いて、 手計算の答えとどれくらい合うか考察せよ。 WebClassの「プログラム課題6」から、 単位荷重法の手計算を撮影した画像と プログラム本体（例えば hone2sj2.f90 とか）と、 出力ファイル（例えば hone2kekka.out とか）を それぞれアップロードせよ。 また、最後のコメント欄に、手計算とプログラムの計算とを比較した考察や、 うまく実行できなかった場合は、 どういう症状で実行できないのかの説明を書き込むこと。
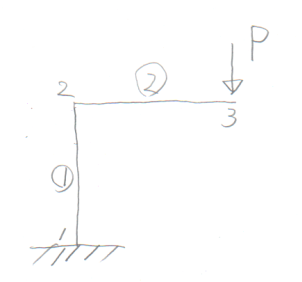学籍番号の末尾が1か8の人。
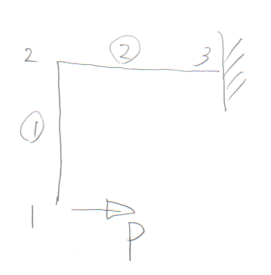学籍番号の末尾が2か9の人。
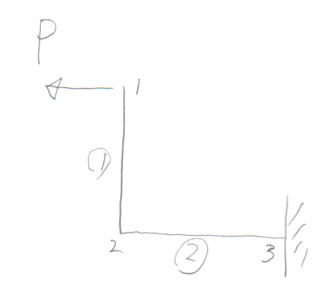学籍番号の末尾が3か0の人。
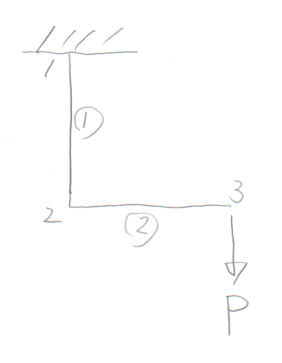学籍番号の末尾が4か6の人。
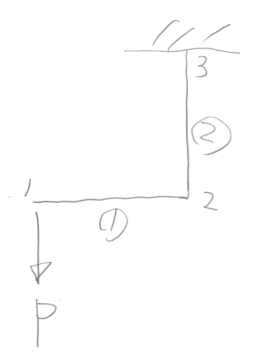学籍番号の末尾が5か7の人。
implicit real*8(a-h, o-z)
dimension f(27),& !節点力ベクトル
& d(27),& !節点変位ベクトル
& x(27),& !境界条件（拘束節点に0, その他に1が入る)
& ss(27,27),& !全体剛性行列
& xv(9),xw(9),xt(9),& !節点ごとの変位境界条件:v,w,θ
& fy(9),fz(9),cx(9),& !節点ごとの荷重条件:S,N,M
& idari(9),migi(9),& !各要素の左節点番号、右節点番号
& s(9,6,6),& !要素剛性行列
& th(9),& !各要素の回転角
& t(6,6),& !座標変換行列（1要素ごとに計算）
& s66(6,6),& !要素剛性行列（1要素ごとに移し替える入れ物）
& ts(6,6),& !TK（1要素ごとに計算）
& tst(6,6) !TKT（1要素ごとに計算）
dimension snm(6) !節点力の出力のために追加
!
pi=asin(1.d0)*2.d0
!
nyou=5 !要素数
nset=4 !節点数
!
! 初期化
do n=1,nyou
do i=1,6
do j=1,6
s(n,i,j)=0.d0
end do
end do
end do
!
do i=1,27
d(i)=0.d0
do j=1,27
ss(i,j)=0.d0
end do
end do
!
do i=1,9
xv(i)=1.d0; xw(i)=1.d0; xt(i)=1.d0 !境界条件は1で初期化
fy(i)=0.d0; fz(i)=0.d0; cx(i)=0.d0
end do
!
! 例題1
! 要素1の剛性マトリクス
el=1000.d0 !1本のL(mm)
ea=10.d3*10.d0**2 !EA(N)
ei=10.d3*10.d0**4/12.d0 !EI(N/mm^2・mm^4)
s(1,2,2)= ea/el ; s(1,2,5)= -ea/el
s(1,5,2)= -ea/el ; s(1,5,5)= ea/el
s(1,1,1)= 12.d0*ei/el**3; s(1,1,3)= -6.d0*ei/el**2
s(1,1,4)=-12.d0*ei/el**3; s(1,1,6)= -6.d0*ei/el**2
s(1,3,1)= -6.d0*ei/el**2; s(1,3,3)= 4.d0*ei/el
s(1,3,4)= 6.d0*ei/el**2; s(1,3,6)= 2.d0*ei/el
s(1,4,1)=-12.d0*ei/el**3; s(1,4,3)= 6.d0*ei/el**2
s(1,4,4)= 12.d0*ei/el**3; s(1,4,6)= 6.d0*ei/el**2
s(1,6,1)= -6.d0*ei/el**2; s(1,6,3)= 2.d0*ei/el
s(1,6,4)= 6.d0*ei/el**2; s(1,6,6)= 4.d0*ei/el
! 要素2~4の剛性マトリクス
do k=2,4
do i=1,6
do j=1,6
s(k,i,j)=s(1,i,j)
end do
end do
end do
! 要素5の剛性マトリクス
el=1000.d0*sqrt(2.d0) !1本のL(mm)
s(5,2,2)= ea/el ; s(5,2,5)= -ea/el
s(5,5,2)= -ea/el ; s(5,5,5)= ea/el
s(5,1,1)= 12.d0*ei/el**3; s(5,1,3)= -6.d0*ei/el**2
s(5,1,4)=-12.d0*ei/el**3; s(5,1,6)= -6.d0*ei/el**2
s(5,3,1)= -6.d0*ei/el**2; s(5,3,3)= 4.d0*ei/el
s(5,3,4)= 6.d0*ei/el**2; s(5,3,6)= 2.d0*ei/el
s(5,4,1)=-12.d0*ei/el**3; s(5,4,3)= 6.d0*ei/el**2
s(5,4,4)= 12.d0*ei/el**3; s(5,4,6)= 6.d0*ei/el**2
s(5,6,1)= -6.d0*ei/el**2; s(5,6,3)= 2.d0*ei/el
!
!do i=1,6
!print'(9f10.2)',(s(1,i,j),j=1,9)
!end do
!print*
!!
!
!
!各要素の左節点番号、右節点番号
idari(1)=1; migi(1)=2
idari(2)=2; migi(2)=3
idari(3)=3; migi(3)=4
idari(4)=1; migi(4)=4
idari(5)=1; migi(5)=3
!
!各要素の回転角（上の左右節点番号がz軸に横たわる状態からの）
th(1)=0.d0
th(2)=pi+pi/2.d0
th(3)=pi
th(4)=pi+pi/2.d0
th(5)=pi+pi*3.d0/4.d0
!
!
!境界条件
xv(4)=0.d0!; xw(4)=0.d0; xt(4)=0.d0
xv(3)=0.d0; xw(3)=0.d0!; xt(3)=0.d0
!
!
do i=1,9
x(3*i-2)=xv(i)
x(3*i-1)=xw(i)
x(3*i)=xt(i)
end do
!
!載荷条件
!cx(2)=1.d0 ! 例題1
fz(2)=200!N
!
do i=1,9
f(3*i-2)=fy(i)
f(3*i-1)=fz(i)
f(3*i)=cx(i)
end do
!
!
!要素ごとのTKTの計算
do n=1,nyou
!
! 座標変換マトリクス
!
call zahyou(t,th(n))
!
do i=1,6
do j=1,6
s66(i,j)=s(n,i,j)
end do
end do
!
call mxtmx(t,s66,ts)
!
call mxmx(ts,t,tst)
!
!do i=1,6
!print'(9f10.2)',(tst(i,j),j=1,9)
!end do
!print*
!!!
!!重ねあわせ
i1=3*idari(n)-2
i2=3*idari(n)-1
i3=3*idari(n)
m1=3*migi(n)-2
m2=3*migi(n)-1
m3=3*migi(n)
!
ss(i1,i1)=ss(i1,i1)+tst(1,1)
ss(i1,i2)=ss(i1,i2)+tst(1,2)
ss(i1,i3)=ss(i1,i3)+tst(1,3)
ss(i1,m1)=ss(i1,m1)+tst(1,4)
ss(i1,m2)=ss(i1,m2)+tst(1,5)
ss(i1,m3)=ss(i1,m3)+tst(1,6)
!
ss(i2,i1)=ss(i2,i1)+tst(2,1)
ss(i2,i2)=ss(i2,i2)+tst(2,2)
ss(i2,i3)=ss(i2,i3)+tst(2,3)
ss(i2,m1)=ss(i2,m1)+tst(2,4)
ss(i2,m2)=ss(i2,m2)+tst(2,5)
ss(i2,m3)=ss(i2,m3)+tst(2,6)
!
ss(i3,i1)=ss(i3,i1)+tst(3,1)
ss(i3,i2)=ss(i3,i2)+tst(3,2)
ss(i3,i3)=ss(i3,i3)+tst(3,3)
ss(i3,m1)=ss(i3,m1)+tst(3,4)
ss(i3,m2)=ss(i3,m2)+tst(3,5)
ss(i3,m3)=ss(i3,m3)+tst(3,6)
! !
!
ss(m1,i1)=ss(m1,i1)+tst(4,1)
ss(m1,i2)=ss(m1,i2)+tst(4,2)
ss(m1,i3)=ss(m1,i3)+tst(4,3)
ss(m1,m1)=ss(m1,m1)+tst(4,4)
ss(m1,m2)=ss(m1,m2)+tst(4,5)
ss(m1,m3)=ss(m1,m3)+tst(4,6)
!
ss(m2,i1)=ss(m2,i1)+tst(5,1)
ss(m2,i2)=ss(m2,i2)+tst(5,2)
ss(m2,i3)=ss(m2,i3)+tst(5,3)
ss(m2,m1)=ss(m2,m1)+tst(5,4)
ss(m2,m2)=ss(m2,m2)+tst(5,5)
ss(m2,m3)=ss(m2,m3)+tst(5,6)
!
ss(m3,i1)=ss(m3,i1)+tst(6,1)
ss(m3,i2)=ss(m3,i2)+tst(6,2)
ss(m3,i3)=ss(m3,i3)+tst(6,3)
ss(m3,m1)=ss(m3,m1)+tst(6,4)
ss(m3,m2)=ss(m3,m2)+tst(6,5)
ss(m3,m3)=ss(m3,m3)+tst(6,6)
!
!
end do !n要素について
!!
!!
!do i=1,8
!print'(8f10.3)', (ss(i,j),j=1,8)
!end do
!print*
!!
! 境界条件を入れる
do i=1,nset*3
do j=1,nset*3
ss(i,j)=x(i)*ss(i,j)
ss(j,i)=x(i)*ss(j,i)
end do
end do
do i=1,nset*3
if(x(i)<1.d-3) then
ss(i,i)=1.d0
end if
end do
!!
!!
!do i=1,9
!print'(9f10.2)',(ss(i,j),j=1,9)
!end do
!
!print*,'f=',(f(j),j=1,18)
!
!
call gausu(nset*3,ss,d,f)
!
!print*
!do i=1,8
!print'(8f10.3)', (ss(i,j),j=1,8)
!end do
!
do n=1,nset
print*,'節点番号：',n,'v=',d(n*3-2),'w=',d(n*3-1), 'th=',d(n*3)
end do
!追加
print'(A)',' 曲げモーメントの単位に注意!'
!要素ごとのTKTの計算
do n=1,nyou
!
! 座標変換マトリクス
!
call zahyou(t,th(n))
!
do i=1,6
do j=1,6
s66(i,j)=s(n,i,j)
end do
end do
!
call mxtmx(t,s66,ts)
!
call mxmx(ts,t,tst)
!
snm=0.0
do i=1,6
do j=1,3
snm(i)=snm(i)+tst(i,j)*d((idari(n)-1)*3+j)
enddo
do j=4,6
snm(i)=snm(i)+tst(i,j)*d((migi(n)-1)*3+j-3)
enddo
enddo
print'(A,I2,A,I2,A,f15.10,A,I2,A,f15.10,A,I2,A,f15.10)','部材番号： ',n,&
&' S(',idari(n),')=',snm(1),' ,N(',idari(n),')=',snm(2),' ,M(',idari(n),')=',snm(3)
print'(A,A,I2,A,f15.10,A,I2,A,f15.10,A,I2,A,f15.10)',' ',&
&' S(',migi(n),')=',snm(4),' ,N(',migi(n),')=',snm(5),' ,M(',migi(n),')=',snm(6)
!
end do !n要素について
!ここまで追加
!print*,'d=',(d(j),j=1,18)
end
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!1!
! 以上がメインプログラム
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!1!
!
subroutine mxmx(a,b,c)
implicit real*8(a-h, o-z)
dimension a(6,6), b(6,6), c(6,6)
!
!
do i=1,6
do j=1,6
c(i,j)=0.
do k=1,6
c(i,j)=c(i,j)+a(i,k)*b(k,j)
end do
end do
end do
!
return
end
!
subroutine zahyou(t,theta)
implicit real*8(a-h, o-z)
dimension t(6,6)
do i=1,3
do j=1,3
t(i+3,j)=0.d0
t(i,j+3)=0.d0
end do
end do
t(1,1)= cos(theta)
t(1,2)= sin(theta)
t(2,1)=-sin(theta)
t(2,2)= cos(theta)
t(3,3)=1.d0
t(4,4)=t(1,1)
t(4,5)=t(1,2)
t(5,4)=t(2,1)
t(5,5)=t(2,2)
t(6,6)=1.d0
return
end
!
subroutine mxtmx(a,b,c)
implicit real*8(a-h, o-z)
dimension a(6,6), b(6,6), c(6,6)
!
do i=1,6
do j=1,6
c(i,j)=0.
do k=1,6
c(i,j)=c(i,j)+a(k,i)*b(k,j)
end do
end do
end do
!
!
return
end
!
!
subroutine gausu(n,a,x,b)
implicit real*8(a-h, o-z)
!dimension a(n,n),x(n),b(n)
dimension a(27,27),x(27),b(27)
!
!ガウスの消去法の参考としたのは、
!名取亮「すうがくぶっくす12 線形計算」(朝倉書店)p.10-15
!!
!print*
!do i=1,8
!print'(8f10.3)', (a(i,j),j=1,8)
!end do
!
!
do k=1,n-1 !a(k,k)を消去
do i=k+1,n !k+1行からn行まで
do j=k+1,n !k+1列からn列まで
a(i,j)=a(i,j)-a(k,j)*a(i,k)/a(k,k)
end do
b(i)=b(i)-b(k)*a(i,k)/a(k,k)
end do
end do
!
! 後退代入
x(n)=b(n)/a(n,n)
do k=n,1,-1
akjxj=0.d0
do j=k+1,n
akjxj=akjxj+a(k,j)*x(j)
end do
x(k)=(b(k)-akjxj)/a(k,k)
end do
!
return
end
!
!