
マトリクス構造解析オンライン授業用テキスト
第12回オンライン授業
小さい字は補足説明なので、読み飛ばしてもいいです。
今回は、プログラムを使ってトラスの問題を解いてみよう。 第5回で2要素について手計算で解いたトラスの 問題を、もっと部材数の多い普通のトラスについて、 プログラムで解いてみようという趣旨だ。 本来であれば、プログラムを組むところからやってもらうのが望ましいが、 この授業の枠内で、これぐらいのプログラムを組めるようになってもらうのは、 なかなか難しいので、ここでは、こちらが用意したプログラムを使って 解いてもらうことにする。
まず、Windows日本語版の人は、 以下のtorasu2sj.f90を、 C:\TDM-GCC-64 の中にダウンロードする。 日本語版以外のWindowsの人は、以下のtorasu2.f90を C:\TDM-GCC-64 の中にダウンロードする。 日本語版以外のWindowsの場合、下記のtorasu2.f90でも日本語をうまく 表示できないかもしれないが、その場合は、 下記のプログラムソースを参照して、 print文の中の'節点番号'や'部材番号'のところを、 自分のパソコンで扱える言語の文字に書き換えてもよい (文字化けしても、何が表示されているか推測できるなら、そのままでもよい)。 ダウンロードするときは、 ブラウザーによもるが、 以下のファイル名を右クリックして「名前をつけてリンク先を保存」 のような方法でファイル自体を保存する。 ファイルをブラウザーで表示してから保存したりすると、 ウェブページとしてhtmlファイルに変換されたものが保存されてしまうこともあるが、 そうではなく、ファイル自体をそのままダウンロードする。 ちなみに、このプログラムは、後藤が 節点変位だけ出すように作ったプログラムを数年前に当時 大学院生だった 近藤さんが節点力も出せるように改造してくれたものである。
 では、このtorasu2sj.f90の使い方を説明するために、
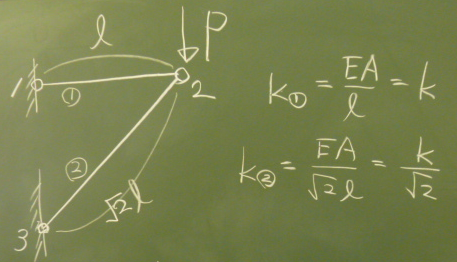
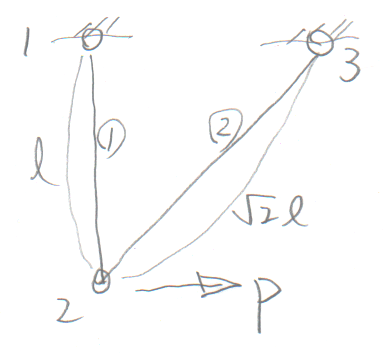
第5回の2要素トラスを
torasu2sj.f90で解く手順を説明する。
では、このtorasu2sj.f90の使い方を説明するために、
第5回の2要素トラスを
torasu2sj.f90で解く手順を説明する。
torasu2sj.f90をテキストエディター(ワードパッドなど)で開き、 上の方の、以下のように書いてあるところを見つける。
pi=asin(1.d0)*2.d0 nyou=5 !要素数 nset=4 !節点数
nyouは要素数、nsetは節点数を表している。 上記の2要素トラスの例題は、要素数が2要素で、 節点数が3個だから、ここを以下のように書き換える。
pi=asin(1.d0)*2.d0 nyou=2 !要素数 nset=3 !節点数
次に、もう少し下の以下のように書いてあるところを見つける。
E=10.d3!MPa ell=1000.d0!mm a=10.d0**2!mm^2 sk1=E*a/ell ! 要素1の剛性マトリクス s(1,2,2)= sk1; s(1,2,4)=-sk1 s(1,4,2)=-sk1; s(1,4,4)= sk1
Eはヤング率、ellは要素の長さ、aは断面積、sk1は、
要素①の ばね定数$k_{①}$を表している。
プログラムで各要素の要素剛性方程式は、
その下に書かれているs(1,2,2)みたいな配列で与えている。
s(1,2,2)の最初の1が、要素①という意味で、
次の2,2は、$k_{①}$の2行2列の成分$k^{①}_{2,2}$を表している。
ここで、各要素の局所系の要素剛性方程式を与えていきたいのだが、
各要素の局所系の要素剛性方程式は、
第4回でやったように
以下のような形をしている。
$
\left(
\begin{array}{c}
S_{1}^{\ell}\\
N_{1}^{\ell}\\
S_{2}^{\ell}\\
N_{2}^{\ell}
\end{array}
\right)
=
\left(
\begin{array}{rrrr}
0 & 0 & 0 & 0 \\
0 & k & 0 & -k \\
0 & 0 & 0 & 0 \\
0 & -k & 0 & k \\
\end{array}
\right)
\left(
\begin{array}{c}
v_{1}^{\ell}\\
w_{1}^{\ell}\\
v_{2}^{\ell}\\
w_{2}^{\ell}
\end{array}
\right)
$
つまり、各要素について、2行2列と4行4列に、その要素のばね定数$k$を、
2行4列と、4行2列に、$-k$を与える。
その他の成分は、あらかじめ初期化しているので、
改めて0を与えなくてもよい。
例えば、要素①の ばね定数を$k_{①}=\frac{EA}{\ell}$で与えるとすると、
$E$や$A$や$\ell$を
E=10.d3, ell=1000.d0, a=10.d0**2みたいに与えておいて、
それからsk1=E*a/ellとすれば、sk1に$\frac{EA}{\ell}$が代入されるから、
これを要素①の剛性方程式の$k_{①}$として、
s(1,2,2)= sk1; s(1,2,4)=-sk1みたいに与えていけばよい。
さて、プログラムで計算するには、$E$や$A$や$\ell$には具体的な値を 入れなければならない。 今回は、プログラムがちゃんと動いているかどうかの確認のため、 $E=A=1$, 要素①について$\ell_{①}=1$, 要素②について$\ell_{②}=\sqrt{2}$として計算してみる。 プログラムの動作確認の際に、 各種のパラメータをとりあえず全部「1」にして計算してみるという ことはよくやるが、これはこれで注意が必要である。 ヤング率も断面積も長さも全部「1」という構造は、 実際には、ものすごく柔らかいフニャフニャの材料だったり、 逆にものすごく固い剛体のような材料だったり、 ありえない構造を解いていることになる。 梁の弾性計算程度であれば、そういう変な値で解いても、 まあ、正解が求まるかもしれないが、 あまりに極端な材料であるために、計算できなくなったり、 おかしな値が出ることもある。 そういうことを避けるためには、 自分が想像しやすい大きさの現実的な材料で解いてみるのがよい。 プログラム内に書かれている E=10.d3!MPa は、木材程度のヤング率で、 10mm$\times$10mmの角材ぐらいの太さ(a=10.d0**2!mm^2)で、 1m(ell=1000.d0!mm)ぐらいの部材を想定したものだろう。 そうすれば、10mm角の長さ1mの角材でトラスを組んで、 人間1人(50kgfとか)ぐらいがぶらさがったら、何mmぐらいたわみそうかとか、 ある程度の予測ができる。 そういう予測のできる問題で解いてみるということも重要だ。 なのだが、今回は、出てきた数値が単位荷重法の理論値と比較しやすいことを 優先して $E=A=1$, 要素①について$\ell_{①}=1$, 要素②について$\ell_{②}=\sqrt{2}$として計算してみる。 つまり、$k_{①}=\frac{EA}{\ell}=1$, $\;\;k_{②}=\frac{1}{\sqrt{2}}$として 計算する ということである。 まず、要素①について、以下のように E=1., ell=1., a=1.と与えてやれば、 sk1=E*a/ellは1になる。
E=1. ell=1. a=1. sk1=E*a/ell ! 要素1の剛性マトリクス s(1,2,2)= sk1; s(1,2,4)=-sk1 s(1,4,2)=-sk1; s(1,4,4)= sk1
次に、その下の要素2の剛性マトリクスのところで、 $k_{②}$を与えているsk2には、以下のように$\frac{k_{①}}{\sqrt{2}}$を与える。 sqrt(2.)は、$\sqrt{2.0}$のことである。
! 要素2の剛性マトリクス sk2=sk1/sqrt(2.) s(2,2,2)= sk2; s(2,2,4)=-sk2 s(2,4,2)=-sk2; s(2,4,4)= sk2
今回は2要素しかないので、その下の要素3以降の剛性マトリクスは 与える必要がない。 要素3以降の剛性マトリクスの部分は、削除するか、 以下のように「!」を入れてコメントにする。
! 要素3の剛性マトリクス !s(3,2,2)= sk3; s(3,2,4)=-sk3 !s(3,4,2)=-sk3; s(3,4,4)= sk3 ! 要素4の剛性マトリクス !sk4=sk1 !s(4,2,2)= sk4; s(4,2,4)=-sk4 !s(4,4,2)=-sk4; s(4,4,4)= sk4 ! 要素5の剛性マトリクス !sk5=sk1/sqrt(2.d0) !s(5,2,2)= sk5; s(5,2,4)=-sk5 !s(5,4,2)=-sk5; s(5,4,4)= sk5
次に各要素の節点番号を与える。 剛性マトリクスの下の以下のように書いているところを見つける。
!各要素の左節点番号、右節点番号 idari(1)=1; migi(1)=2 idari(2)=2; migi(2)=3 idari(3)=3; migi(3)=4 idari(4)=1; migi(4)=4 idari(5)=1; migi(5)=3
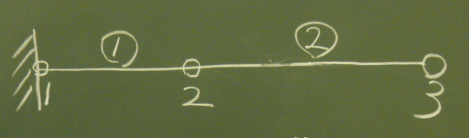 idari(1)の(1)は、要素①ということで、
idariというのは、左節点番号ということである。
migi(1)というのは、要素①の右節点番号ということである。
例えば、今回の2要素トラスについて、
まずは、図のようにすべての要素を$z$軸方向に並べて初期状態を決める。
トラスが一筆書きで書けるなら、なるべく1本につなげた方が、
設定しやすい。
要素①の左節点は1で右節点は2だから、
idari(1)=1; migi(1)=2 となる(このまま修正不要)。
要素②の左節点は2で右節点は3だから、
idari(2)=2; migi(2)=3(これも、このまま修正不要)。
今回は、2要素なので、要素③以降はない。
よって、idari(3)以降の行は、以下のように「!」をつけてコメントにする。
「!」と「i」が並んでいるとわかりにくいのでスペースを1つ入れた。
idari(1)の(1)は、要素①ということで、
idariというのは、左節点番号ということである。
migi(1)というのは、要素①の右節点番号ということである。
例えば、今回の2要素トラスについて、
まずは、図のようにすべての要素を$z$軸方向に並べて初期状態を決める。
トラスが一筆書きで書けるなら、なるべく1本につなげた方が、
設定しやすい。
要素①の左節点は1で右節点は2だから、
idari(1)=1; migi(1)=2 となる(このまま修正不要)。
要素②の左節点は2で右節点は3だから、
idari(2)=2; migi(2)=3(これも、このまま修正不要)。
今回は、2要素なので、要素③以降はない。
よって、idari(3)以降の行は、以下のように「!」をつけてコメントにする。
「!」と「i」が並んでいるとわかりにくいのでスペースを1つ入れた。
!各要素の左節点番号、右節点番号 idari(1)=1; migi(1)=2 idari(2)=2; migi(2)=3 ! idari(3)=3; migi(3)=4 ! idari(4)=1; migi(4)=4 ! idari(5)=1; migi(5)=3
次に各要素の回転角を与える。 節点番号の下の以下のように書いてある場所を見つける。
!各要素の回転角(上の左右節点番号がz軸に横たわる状態からの) th(1)=0.d0 th(2)=pi+pi/2.d0 th(3)=pi th(4)=pi+pi/2.d0 th(5)=pi+pi*3.d0/4.d0
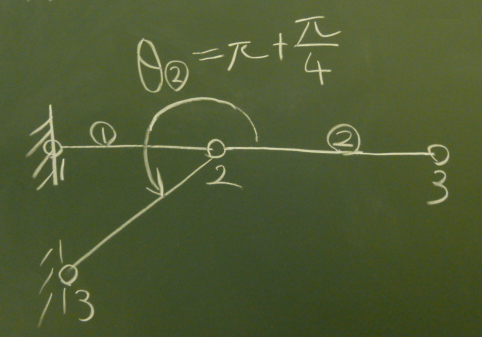 th(1)というのは、要素①の初期状態からの回転量を、
左節点の$x$軸右ねじ回り($yz$平面では反時計回り)の回転角$\theta_{①}$で与える。
要素①は、水平で初期状態から回転しないので、$\theta_{①}=0$である。
つまり、th(1)=0.d0でよい。
0.d0の.d0は、$\times 10^{0}$という意味だと思っておいてほしい。
0.と書いてもよい。
一方、要素②は、斜めになっているので、回転角$\theta_{②}$は0ではない。
要素②の左節点(つまり節点2)の
初期状態からの$x$軸右ねじ回りの回転角は、
図のように$\pi+\frac{\pi}{4}$である。
よって、th(2)=pi+pi/4.と書き換える必要がある。
要素③以降はないので、th(3)以降の行はコメントにする。
th(1)というのは、要素①の初期状態からの回転量を、
左節点の$x$軸右ねじ回り($yz$平面では反時計回り)の回転角$\theta_{①}$で与える。
要素①は、水平で初期状態から回転しないので、$\theta_{①}=0$である。
つまり、th(1)=0.d0でよい。
0.d0の.d0は、$\times 10^{0}$という意味だと思っておいてほしい。
0.と書いてもよい。
一方、要素②は、斜めになっているので、回転角$\theta_{②}$は0ではない。
要素②の左節点(つまり節点2)の
初期状態からの$x$軸右ねじ回りの回転角は、
図のように$\pi+\frac{\pi}{4}$である。
よって、th(2)=pi+pi/4.と書き換える必要がある。
要素③以降はないので、th(3)以降の行はコメントにする。
!各要素の回転角(上の左右節点番号がz軸に横たわる状態からの) th(1)=0.d0 th(2)=pi+pi/4. ! th(3)=pi ! th(4)=pi+pi/2.d0 ! th(5)=pi+pi*3.d0/4.d0
次は境界条件である。 回転角の下の以下のように書いてあるところを見つける。
!境界条件 xv(3)=0.d0; xw(3)=0.d0 xv(4)=0.d0!; xw(4)=0.d0
境界条件は、拘束されている節点の拘束されている変位 ($v$や$w$)を0にすることで与える。 $v_{1}$はxv(1), $w_{2}$はxw(2)のように表す。 例えば、節点3で$v_{3}=0$であれば、xv(3)=0と与える。 今回は、節点1と節点3が固定端で、 $v_{1}=w_{1}=v_{3}=w_{3}=0$だから、 以下のよう書き換える。
!境界条件 xv(1)=0.d0; xw(1)=0.d0 xv(3)=0.d0; xw(3)=0.d0
!; xw(4)=0.d0 の!を消し忘れたりすると、 そこから改行までがコメントのままになってしまうので、 以下のように1行ずつ書いてもよい。
xv(1)=0.d0 xw(1)=0.d0 xv(3)=0.d0 xw(3)=0.d0
最後に載荷条件である。境界条件のちょっと下の 以下のような場所を見つける。
!載荷条件 fz(2)=200.d0 !N
荷重は、$y$方向荷重がfy(), $z$方向荷重がfz()で、 荷重を与える節点番号を()内に書く。 剛性マトリクスのばね定数を与えるところで述べたように、 荷重も、現実的な荷重を与えるべきだが、 今回は、理論値との比較がしやすいように$P=1$ということにする。 節点2の$y$方向に1だから、fy(2)=1.とすればよい。 2022/7/7まで、間違ってここをfy(1)=1.と書いてました。すいません。
!載荷条件 fy(2)=1.
プログラムの修正が終わったら、
"torasu2sj.f90"に上書き保存してもいいが、
エラーが出たときに、エラーが出ないプログラムを少しずつ修正しながら、
どの段階でエラーが出るのか比較できるように、
元のプログラムは"torasu2sj.f90"のまま保管しておいて、
修正したプログラムは名前を変えて、例えば"torasu2sj_gotou.f90"みたいに
して保存した方がいいかもしれない。
プログラムをコンパイルして実行すると、
画像のような画面が表示される。
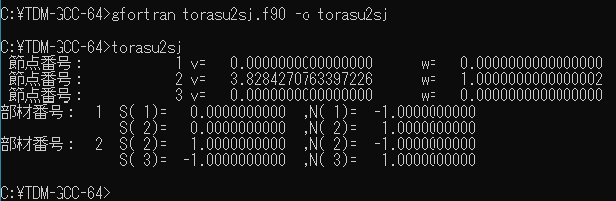
節点番号: 1 v= 0.0000000000000000 w= 0.0000000000000000 節点番号: 2 v= 3.8284270763397226 w= 1.0000000000000002 節点番号: 3 v= 0.0000000000000000 w= 0.0000000000000000
これは、節点ごとの節点変位が並んでいる。
上から順に1行目が、$v_{1}, w_{1}$, 2行目が$v_{2}, w_{2}$, 3行目が$v_{3}, w_{3}$である。
境界条件から、$v_{1}=0, w_{1}=0, v_{3}=0, w_{3}=0$はいいだろう。
第5回で単位荷重法で解いた答えによると、
$v_{2}=(1+2\sqrt{2})\frac{P\ell}{EA}$,
$\;w_{2}=\frac{P\ell}{EA}$だったから、$P=E=A=\ell=1$を代入すると、
$v_{2}=(1+2\sqrt{2})=3.828427125\;\;\;$,
$w_{2}=1$となる。
$v_{2}$については、7桁まで一致している。
$w_{2}$については、最後の桁に2が入っているが、この辺は数値計算による誤差ということだ。
次に節点力だが、
以下の部材番号: 1は、要素①を、部材番号: 2は要素②を表し、
S(1)やN(1)は$S_{1}$や$N_{1}$を表す。つまり、
部材番号: 1のところのS(2)は$S_{2}^{①}$を表し、
部材番号: 2のところのS(2)は$S_{2}^{②}$を表す。
部材番号: 1 S( 1)= 0.0000000000 ,N( 1)= -1.0000000000
S( 2)= 0.0000000000 ,N( 2)= 1.0000000000
部材番号: 2 S( 2)= 1.0000000000 ,N( 2)= -1.0000000000
S( 3)= -1.0000000000 ,N( 3)= 1.0000000000
第5回でマトリクスを手計算で解いた答えによると、
要素①の要素剛性方程式に節点変位を代入
$
\left(
\begin{array}{c}
S_{1}\\
N_{1}\\
S_{2}^{①}\\
N_{2}^{①}
\end{array}
\right)
=
\left(
\begin{array}{rrrr}
0 & 0 & 0 & 0 \\
0 & k & 0 & -k \\
0 & 0 & 0 & 0 \\
0 & -k & 0 & k
\end{array}
\right)
\left(
\begin{array}{c}
0\\
0\\
(1+2\sqrt{2})\frac{P}{k}\\
\frac{P}{k}
\end{array}
\right)
=
\left(
\begin{array}{c}
0\\
-P\\
0 \\
P
\end{array}
\right)
$
要素②の要素剛性方程式に節点変位を代入
$
\left(
\begin{array}{c}
S_{2}^{②}\\
N_{2}^{②}\\
S_{3}\\
N_{3}
\end{array}
\right)
=
\frac{k}{2\sqrt{2}}
\left(
\begin{array}{rrrr}
1 & -1 & -1 & 1 \\
-1 & 1 & 1 & -1 \\
-1 & 1 & 1 & -1 \\
1 & -1 & -1 & 1
\end{array}
\right)
\left(
\begin{array}{c}
(1+2\sqrt{2})\frac{P}{k}\\
\frac{P}{k}\\
0\\
0
\end{array}
\right)
=
\left(
\begin{array}{c}
P\\
-P\\
-P \\
P
\end{array}
\right)
$
と求まっていたが、$P=1$を代入すれば、
プログラムで解いた答えと一致していることが確認できる。
以下の2要素トラス(自分の学籍番号のもの)の 載荷点の節点変位($v, w$)を単位荷重法で求めよ。 部材の伸び剛性はすべて$EA$とする。 斜めの部材は水平方向から$45^{\circ}$傾いていて、 その他の部材は、水平か鉛直である。 次に、$P=E=A=\ell=1.$として、 それをtorasu2sj.f90で解いて、 手計算の答えとどれくらい合うか考察せよ。 WebClassの「プログラム課題4」から、 単位荷重法の手計算を撮影した画像と プログラム本体(例えば torasu2sj_gotou.f90 とか)と、 出力ファイル(例えば kekka.out とか)を それぞれアップロードせよ。 どうしてもエラーが取れないなどの場合は、 kekka.outの代わりに、エラー画面等 を写真で撮影したものをアップロードする。 また、最後のコメント欄に、手計算とプログラムの計算とを比較した考察や、 うまく実行できなかった場合は、 どういう症状で実行できないのかの説明を書き込むこと。
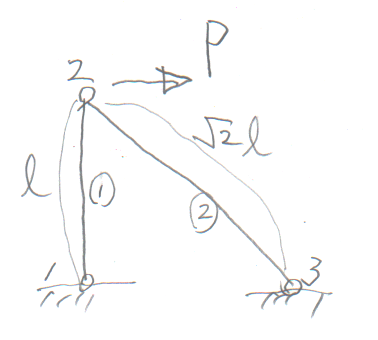 学籍番号の末尾が1か6の人。
学籍番号の末尾が1か6の人。
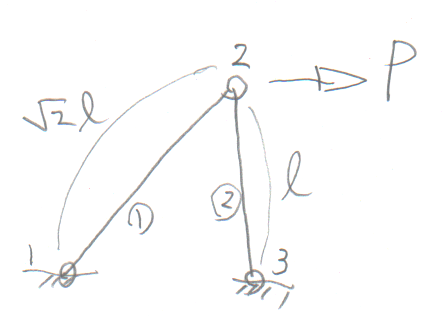 学籍番号の末尾が2か7の人。
学籍番号の末尾が2か7の人。
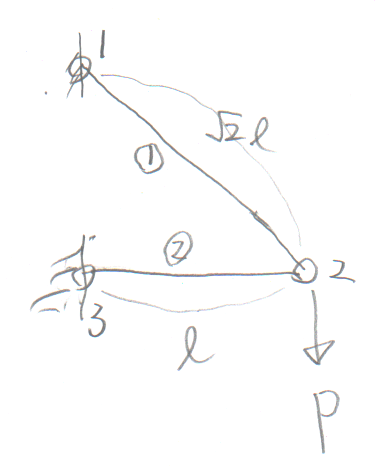 学籍番号の末尾が3か8の人。
学籍番号の末尾が3か8の人。
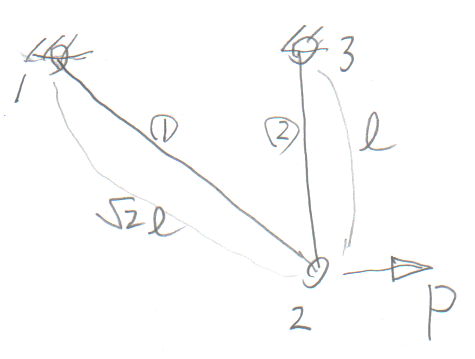 学籍番号の末尾が4か9の人。
学籍番号の末尾が4か9の人。
 学籍番号の末尾が5か0の人。
学籍番号の末尾が5か0の人。
implicit real*8(a-h, o-z)
dimension f(18),& !節点力ベクトル
& d(18),& !節点変位ベクトル
& x(18),& !境界条件(拘束節点に0, その他に1が入る)
& ss(18,18),& !全体剛性行列
& xv(9),xw(9),& !節点ごとの変位境界条件
& fy(9),fz(9),& !節点ごとの荷重条件
& idari(9),migi(9),& !各要素の左節点番号、右節点番号
& s(9,4,4),& !要素剛性行列
& th(9),& !各要素の回転角
& t(4,4),& !座標変換行列(1要素ごとに計算)
& s44(4,4),& !要素剛性行列(1要素ごとに移し替える入れ物)
& ts(4,4),& !TK(1要素ごとに計算)
& tst(4,4) !TKT(1要素ごとに計算)
dimension sn(4) !節点力の出力のために追加
pi=asin(1.d0)*2.d0
nyou=5 !要素数
nset=4 !節点数
! 初期化
do n=1,nyou
do i=1,4
do j=1,4
s(n,i,j)=0.d0
end do
end do
end do
do i=1,18
d(i)=0.d0 !; f(i)=0.d0; x(i)=0.d0
do j=1,18
ss(i,j)=0.d0
end do
end do
do i=1,9
xv(i)=1.d0; xw(i)=1.d0 !境界条件は1で初期化
fy(i)=0.d0; fz(i)=0.d0
end do
E=10.d3!MPa
ell=1000.d0!mm
a=10.d0**2!mm^2
sk1=E*a/ell
! 要素1の剛性マトリクス
s(1,2,2)= sk1; s(1,2,4)=-sk1
s(1,4,2)=-sk1; s(1,4,4)= sk1
! 要素2の剛性マトリクス
sk2=sk1
s(2,2,2)= sk2; s(2,2,4)=-sk2
s(2,4,2)=-sk2; s(2,4,4)= sk2
sk3=sk1
! 要素3の剛性マトリクス
s(3,2,2)= sk3; s(3,2,4)=-sk3
s(3,4,2)=-sk3; s(3,4,4)= sk3
! 要素4の剛性マトリクス
sk4=sk1
s(4,2,2)= sk4; s(4,2,4)=-sk4
s(4,4,2)=-sk4; s(4,4,4)= sk4
! 要素5の剛性マトリクス
sk5=sk1/sqrt(2.d0)
s(5,2,2)= sk5; s(5,2,4)=-sk5
s(5,4,2)=-sk5; s(5,4,4)= sk5
!各要素の左節点番号、右節点番号
idari(1)=1; migi(1)=2
idari(2)=2; migi(2)=3
idari(3)=3; migi(3)=4
idari(4)=1; migi(4)=4
idari(5)=1; migi(5)=3
!各要素の回転角(上の左右節点番号がz軸に横たわる状態からの)
th(1)=0.d0
th(2)=pi+pi/2.d0
th(3)=pi
th(4)=pi+pi/2.d0
th(5)=pi+pi*3.d0/4.d0
!境界条件
xv(3)=0.d0; xw(3)=0.d0
xv(4)=0.d0!; xw(4)=0.d0
do i=1,9
x(2*i-1)=xv(i)
x(2*i)=xw(i)
end do
!
!載荷条件
fz(2)=200.d0 !N
!
do i=1,9
f(2*i-1)=fy(i)
f(2*i)=fz(i)
end do
!
!
!要素ごとのTKTの計算
do n=1,nyou
!
! 座標変換マトリクス
!
call zahyou(t,th(n))
!
do i=1,4
do j=1,4
s44(i,j)=s(n,i,j)
end do
end do
!
call mxtmx(t,s44,ts)
!
call mxmx(ts,t,tst)
!!
!!重ねあわせ
i1=2*idari(n)-1
i2=2*idari(n)
m1=2*migi(n)-1
m2=2*migi(n)
!
ss(i1,i1)=ss(i1,i1)+tst(1,1)
ss(i1,i2)=ss(i1,i2)+tst(1,2)
ss(i1,m1)=ss(i1,m1)+tst(1,3)
ss(i1,m2)=ss(i1,m2)+tst(1,4)
! !
ss(i2,i1)=ss(i2,i1)+tst(2,1)
ss(i2,i2)=ss(i2,i2)+tst(2,2)
ss(i2,m1)=ss(i2,m1)+tst(2,3)
ss(i2,m2)=ss(i2,m2)+tst(2,4)
! !
ss(m1,i1)=ss(m1,i1)+tst(3,1)
ss(m1,i2)=ss(m1,i2)+tst(3,2)
ss(m1,m1)=ss(m1,m1)+tst(3,3)
ss(m1,m2)=ss(m1,m2)+tst(3,4)
! !
ss(m2,i1)=ss(m2,i1)+tst(4,1)
ss(m2,i2)=ss(m2,i2)+tst(4,2)
ss(m2,m1)=ss(m2,m1)+tst(4,3)
ss(m2,m2)=ss(m2,m2)+tst(4,4)
!
!
end do !n要素について
!!
!!
!do i=1,8
!print'(8f10.3)', (ss(i,j),j=1,8)
!end do
!print*
!!
! 境界条件を入れる
do i=1,nset*2
do j=1,nset*2
ss(i,j)=x(i)*ss(i,j)
ss(j,i)=x(i)*ss(j,i)
end do
end do
do i=1,nset*2
if(x(i)<1.d-3) then
ss(i,i)=1.d0
end if
end do
!!
!!
!
!print*,'f=',(f(j),j=1,18)
!
!
call gausu(nset*2,ss,d,f)
!
!print*
!do i=1,8
!print'(8f10.3)', (ss(i,j),j=1,8)
!end do
!
do n=1,nset
print*,'節点番号:',n,'v=',d(n*2-1),'w=',d(n*2)
end do
!追加
!要素ごとのTKTの計算
do n=1,nyou
!
! 座標変換マトリクス
!
call zahyou(t,th(n))
!
do i=1,4
do j=1,4
s44(i,j)=s(n,i,j)
end do
end do
!
call mxtmx(t,s44,ts)
!
call mxmx(ts,t,tst)
!!
sn=0.0
do i=1,4
do j=1,2
sn(i)=sn(i)+tst(i,j)*d((idari(n)-1)*2+j)
enddo
do j=3,4
sn(i)=sn(i)+tst(i,j)*d((migi(n)-1)*2+j-2)
enddo
enddo
print'(A,I2,A,I2,A,f15.10,A,I2,A,f15.10)','部材番号: ',n,&
&' S(',idari(n),')=',sn(1),' ,N(',idari(n),')=',sn(2)
print'(A,A,I2,A,f15.10,A,I2,A,f15.10)',' ',&
&' S(',migi(n),')=',sn(3),' ,N(',migi(n),')=',sn(4)
!
end do !n要素について
!ここまで追加
!print*,'d=',(d(j),j=1,18)
end
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!1!
! 以上がメインプログラム
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!1!
!
subroutine mxmx(a,b,c)
implicit real*8(a-h, o-z)
dimension a(4,4), b(4,4), c(4,4)
!
!
do i=1,4
do j=1,4
c(i,j)=0.
do k=1,4
c(i,j)=c(i,j)+a(i,k)*b(k,j)
end do
end do
end do
!
return
end
!
subroutine zahyou(t,theta)
implicit real*8(a-h, o-z)
dimension t(4,4)
do i=1,2
do j=1,2
t(i+2,j)=0.d0
t(i,j+2)=0.d0
end do
end do
t(1,1)= cos(theta)
t(1,2)= sin(theta)
t(2,1)=-sin(theta)
t(2,2)= cos(theta)
t(3,3)=t(1,1)
t(3,4)=t(1,2)
t(4,3)=t(2,1)
t(4,4)=t(2,2)
return
end
!
subroutine mxtmx(a,b,c)
implicit real*8(a-h, o-z)
dimension a(4,4), b(4,4), c(4,4)
!
do i=1,4
do j=1,4
c(i,j)=0.
do k=1,4
c(i,j)=c(i,j)+a(k,i)*b(k,j)
end do
end do
end do
!
!
return
end
!
!
subroutine gausu(n,a,x,b)
implicit real*8(a-h, o-z)
!dimension a(n,n),x(n),b(n)
dimension a(18,18),x(18),b(18)
!
!ガウスの消去法の参考としたのは、
!名取亮「すうがくぶっくす12 線形計算」(朝倉書店)p.10-15
!!
!print*
!do i=1,8
!print'(8f10.3)', (a(i,j),j=1,8)
!end do
!
!
do k=1,n-1 !a(k,k)を消去
do i=k+1,n !k+1行からn行まで
do j=k+1,n !k+1列からn列まで
a(i,j)=a(i,j)-a(k,j)*a(i,k)/a(k,k)
end do
b(i)=b(i)-b(k)*a(i,k)/a(k,k)
end do
end do
!
! 後退代入
x(n)=b(n)/a(n,n)
do k=n,1,-1
akjxj=0.d0
do j=k+1,n
akjxj=akjxj+a(k,j)*x(j)
end do
x(k)=(b(k)-akjxj)/a(k,k)
end do
!
return
end
!
!