構造力学Iオンライン授業用テキスト
第13回オンライン授業
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
前回やった反力の影響線の場合、 $V_{A}(\zeta)$は支点Aの反力の影響線関数だし、 $V_{B}(\zeta)$は支点Bの反力の影響線関数だし、 という具合に、着目している点(支点Aとか支点Bとか)が決まっていた。 せん断力や曲げモーメントの影響線という場合、 ある着目点（この授業では点Cを使うことにする）での せん断力や曲げモーメントが、荷重の移動に伴ってどう変化するかを 考えることになる。 より一般的には、任意の着目点$z$に対する 影響線関数$S(z,\zeta)$や$M(z,\zeta)$を求めることも できるが、それは、やや難しいので、ここではまず、 具体的な1つの着目点についての影響線を考える。
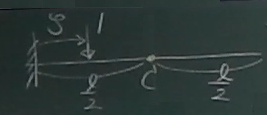
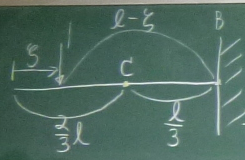
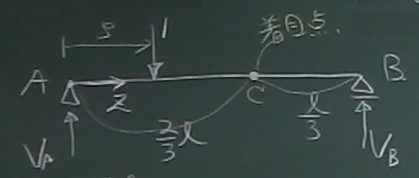ではまず図のように、例えば$z=\frac{2}{3}\ell$の点を着目点Cとし、
点Cでの
せん断力と曲げモーメントの影響線関数
$S(z=\frac{2}{3}\ell, \zeta)$,
$M(z=\frac{2}{3}\ell, \zeta)$
を求めてみる。
着目点の座標をいちいち書くとめんどくさいので、
これらを
$S_{C}(\zeta)$,
$M_{C}(\zeta)$と書くことにする。
まずは、前回の要領で反力の影響線関数を求める。
$\zeta$を定数とみなして
普通に力のつりあいから求めればよいが、時間の関係上、
公式を使うと、
$a=\zeta\,,\; b=\ell-\zeta$だから、
$V_{A}=\frac{\ell-\zeta}{\ell}$
$V_{B}=\frac{\zeta}{\ell}$
と求まる。
内力である
せん断力や曲げモーメントを求める場合、梁を切断して断面力が見えるようにして
やらなければならない。
任意点$z$での$S(z)$や$M(z)$を求めるときは、
第5回でやったように
（場合分けが必要な場合は、場合分けした上で）任意の点$z$で梁を切断したが、
影響線関数を求める場合は、求めるせん断力や曲げモーメントは、
着目点C(今回は$z=\frac{2}{3}\ell$)での値なので、
任意の$z$ではなく、着目点Cで切断する。
すると、
単位荷重が着目点Cより左にある場合と
単位荷重が着目点Cより右にある場合とで場合分けが必要になる。
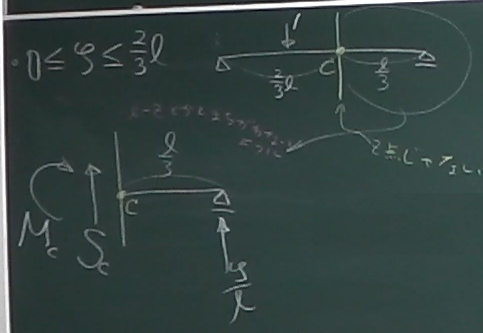
ではまず、
単位荷重が着目点Cより左にある場合(今回の例では$0\le\zeta\le\frac{2}{3}\ell$)
を考える。
梁を着目点Cで2つのピースに切り離し、左側か右側かどちらかのピースを取り出して
つりあいを考える。
単位荷重のないピースの方が楽そうなので、今回は右側のピースを取り出す
ことにする。
右端の反力は、上で$\frac{\zeta}{\ell}$と求まった。
点Cから右端までの長さは、点Cが$z=\frac{2}{3}\ell$だから、
$\frac{\ell}{3}$である。
任意の$z$で切ったわけではないので、$\ell-z$などと混同しないように。
力のつりあいから、
$\sum\downarrow=-S_{C}-\frac{\zeta}{\ell}=0$ よって、
$S_{C}(\zeta)=-\frac{\zeta}{\ell}\;\;\;\;(0\le\zeta\le\frac{2}{3}\ell)$
$\sum_{C}\circlearrowleft=-M_{C}+\frac{\zeta}{\ell}\cdot\frac{\ell}{3}=0$ よって、
$M_{C}(\zeta)=\frac{\zeta}{3}\;\;\;\;(0\le\zeta\le\frac{2}{3}\ell)$
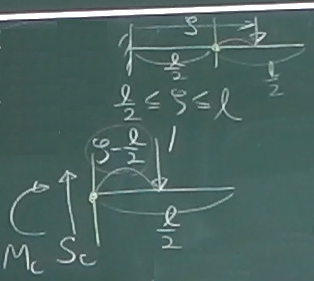
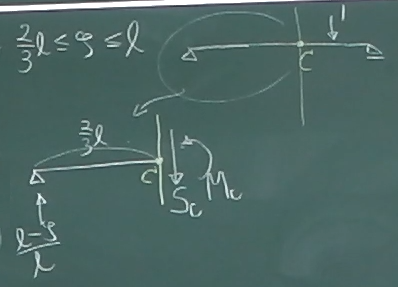次に、
単位荷重が着目点Cより右にある場合(今回の例では$\frac{2}{3}\ell\le \zeta\le\ell$)
を考える。
梁を着目点Cで2つのピースに切り離し、左側か右側かどちらかのピースを取り出して
つりあいを考える。
単位荷重のないピースの方が楽そうなので、今回は左側のピースを取り出す
ことにする。
左端の反力は、上で$\frac{\ell-\zeta}{\ell}$と求まった。
左端から点Cまでの距離は、$\frac{2}{3}\ell$である。
任意の$z$で切ったわけではないので、$z$などと混同しないように。
力のつりあいから、
$\sum\downarrow=-\frac{\ell-\zeta}{\ell}+S_{C}=0$ よって、
$S_{C}(\zeta)=\frac{\ell-\zeta}{\ell}\;\;\;\;(\frac{2}{3}\ell\le \zeta\le\ell)$
$\sum_{C}\circlearrowleft=-\frac{\ell-\zeta}{\ell}\cdot\frac{2}{3}\ell
+M_{C}=0$ よって、
$M_{C}(\zeta)=\frac{2}{3}(\ell-\zeta)\;\;\;\;(\frac{2}{3}\ell\le \zeta\le\ell)$
以上を整理すると、以下のようになる。
$
S_{C}(\zeta)=
\begin{cases}
-\frac{\zeta}{\ell} & \;\;\;\;(0\le\zeta\le\frac{2}{3}\ell)\\
\frac{\ell-\zeta}{\ell} & \;\;\;\;(\frac{2}{3}\ell\le \zeta\le\ell)\\
\end{cases}
\ \\
M_{C}(\zeta)=
\begin{cases}
\frac{\zeta}{3} & \;\;\;\;(0\le\zeta\le\frac{2}{3}\ell)\\
\frac{2}{3}(\ell-\zeta) & \;\;\;\;(\frac{2}{3}\ell\le \zeta\le\ell)\\
\end{cases}
$
ここで注意すべきことは、
$(0\le\zeta\le\frac{2}{3}\ell)$や$(\frac{2}{3}\ell\le \zeta\le\ell)$と
いった領域の意味は、
その領域に荷重がある場合という意味であって、
その領域の$S$や$M$を表しているわけではない。
$S_{C}$や$M_{C}$は、あくまで点C(今回は$z=\frac{2}{3}\ell$)での$S$や$M$を表しているので
混同しないように。
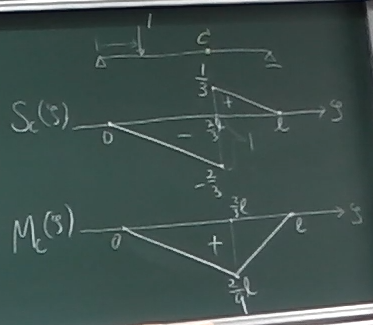横軸を$\zeta$とし、縦軸を$S_{C}(\zeta)$や$M_{C}(\zeta)$として、
影響線を描く。$S$図や$M$図に対応させて、
この授業ではせん断力の影響線は上を正、曲げモーメントの影響線は下を正とする。
$S_{C}(\zeta)$も$M_{C}(\zeta)$も$\zeta$の1次式だから直線である。
領域の両端の値を求めて、それらを直線で結べばよい。
公式を使って手早く描く場合はこちら参照。
$
S_{C}(\zeta)=
\begin{cases}
-\frac{\zeta}{\ell} & \;\;\;\;(0\le\zeta\le\frac{2}{3}\ell)
\;\;\;\;
S_{C}(0)=0,\;\;\;\; S_{C}(\frac{2}{3}\ell)=-\frac{2}{3} \\
\frac{\ell-\zeta}{\ell} & \;\;\;\;(\frac{2}{3}\ell\le \zeta\le\ell)
\;\;\;\; S_{C}(\frac{2}{3}\ell)=\frac{1}{3}
\;\;\;\; S_{C}(\ell)=0
\\
\end{cases}
$
$\zeta=\frac{2}{3}\ell$のところで、$S_{C}$はマイナスからプラスにジャンプしている。
この意味は後で説明する。
荷重が着目点の左にあるときも右にあるときも$\zeta$の係数は$-1$だから、
どちらの直線も傾き$-1$で平行である。
$
M_{C}(\zeta)=
\begin{cases}
\frac{\zeta}{3} & \;\;\;\;(0\le\zeta\le\frac{2}{3}\ell)
\;\;\;\; M_{C}(0)=0,
\;\;\;\; M_{C}(\frac{2}{3}\ell)=\frac{2}{9}\ell
\\
\frac{2}{3}(\ell-\zeta) & \;\;\;\;(\frac{2}{3}\ell\le \zeta\le\ell)
\;\;\;\; M_{C}(\frac{2}{3}\ell)=\frac{2}{9}\ell,
\;\;\;\; M_{C}(\ell)=0
\\
\end{cases}
$
$M_{C}$の方は、点Cでジャンプしない。
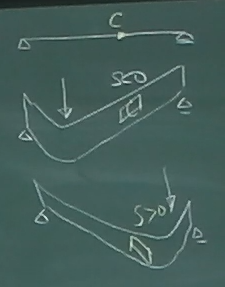さて、せん断力の影響線$S_{C}(\zeta)$が、
着目点Cをまたいで、マイナスからプラスにジャンプする理由だが、
荷重が着目点Cより左にある場合、図のように
着目点Cは右上がりになるから、せん断力はマイナスになる。
一方、荷重が着目点Cより右にある場合は、図のように
着目点Cは右下がりになるから、せん断力はプラスになる。
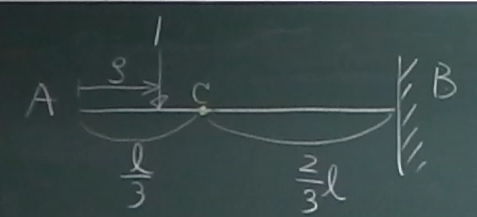
図のような片持ち梁の$z=\frac{\ell}{2}$の点Cでのせん断力、
曲げモーメントの影響線を求めてみよう。
この場合、（反力のない方のピースを取り出すなら）反力を求めなくても、
$S_{C}(\zeta), M_{C}(\zeta)$は求められるが、
前回、既に求めているので、
反力は、$V_{A}(\zeta)=1, \;\;M_{A}(\zeta)=-\zeta$である。
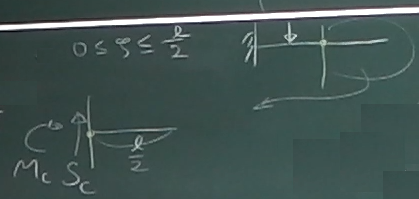まず、梁を切るのは着目点Cと決まっているので、
荷重が着目点Cより左にある場合($0\le\zeta\le\frac{\ell}{2}$)と
荷重が着目点Cより右にある場合($\frac{\ell}{2}\le\zeta\le\ell$)とで
場合分けする。
まず、荷重が着目点Cより左にある場合($0\le\zeta\le\frac{\ell}{2}$)を考える。
梁を着目点Cで2つのピースに切り離し、左側か右側かどちらかのピースを取り出して
つりあいを考える。
単位荷重のないピースの方が楽そうなので、今回は右側のピースを取り出す
ことにする。
点C($z=\frac{\ell}{2}$)から右端までの長さは$\frac{\ell}{2}$である。
任意点$z$で切ったわけではないので、$\ell-z$とかにはならない。
力のつりあいから、
$\sum\downarrow=-S_{C}=0$
よって、
$S_{C}(\zeta)=0\;\;\;\;(0\le\zeta\le\frac{\ell}{2})$
$\sum_{C}\circlearrowleft=-M_{C}=0$ よって、
$M_{C}(\zeta)=0\;\;\;\;(0\le\zeta\le\frac{\ell}{2})$
次に、荷重が着目点Cより右にある場合($\frac{\ell}{2}\le\zeta\le\ell$)を考える。
梁を着目点Cで2つのピースに切り離し、左側か右側かどちらかのピースを取り出して
つりあいを考える。
反力がない方が楽そうなので、今回は単位荷重のある
右側のピースを取り出すことにする。
図のように、梁全体の左端から単位荷重のある位置までの長さが$\zeta$だから、
切断した着目点C($z=\frac{\ell}{2}$)から単位荷重のある位置までの長さは、
$\zeta-\frac{\ell}{2}$となる。
こういうのは、梁の全体を描いて落ち着いて考えるとよい。
力のつりあいから、
$\sum\downarrow=-S_{C}+1=0$
よって、
$S_{C}(\zeta)=1\;\;\;\;(\frac{\ell}{2}\le\zeta\le\ell)$
$\sum_{C}\circlearrowleft=-M_{C}-1(\zeta-\frac{\ell}{2})=0$ よって、
$M_{C}(\zeta)=-(\zeta-\frac{\ell}{2})\;\;\;\;(\frac{\ell}{2}\le\zeta\le\ell)$
もちろん、$M_{C}(\zeta)=\frac{\ell}{2}-\zeta$と書いてもよい。
$\zeta-\frac{\ell}{2}$などの正の長さを正の長さのまま書いておいた方が、
モーメントが正なのか負なのかわかりやすいという程度のことである。
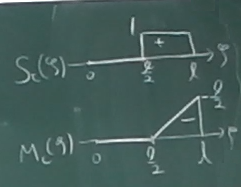以上をまとめて、1次式については各領域の両端の値を求める。
$
S_{C}(\zeta)=
\begin{cases}
0 &\;\;\;\;(0\le\zeta\le\frac{\ell}{2})\\
1 &\;\;\;\;(\frac{\ell}{2}\le\zeta\le\ell)
\\
\end{cases}
$
$
M_{C}(\zeta)=
\begin{cases}
0 &\;\;\;\;(0\le\zeta\le\frac{\ell}{2})\\
-(\zeta-\frac{\ell}{2}) &\;\;\;\;(\frac{\ell}{2}\le\zeta\le\ell)
\;\;\;\;M_{C}(\frac{\ell}{2})=0,\; M_{C}(\ell)=-\frac{\ell}{2}
\end{cases}
$
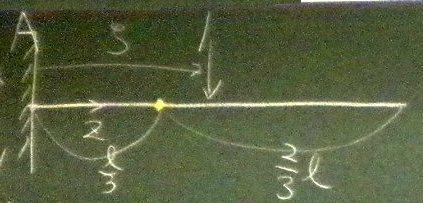
着目点Cでのせん断力、曲げモーメントの影響線関数
$S_{C}(\zeta), M_{C}(\zeta)$を求め、
その影響線（せん断力は上が正、曲げモーメントは下が正）を描け。
答えは、
ここ。
動画の解説は、
第13回 例題。
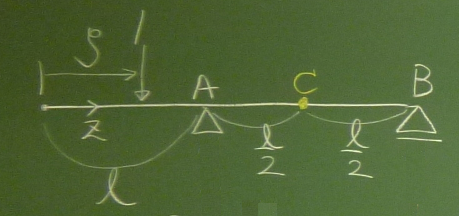ここ。
ここ。
ここ。
2020年度小テスト： 問1, 問2, 問3, 問4, 解答
メモ:
