
構造力学(応用)目次
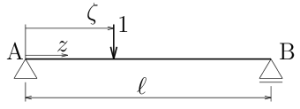 影響線というのは、大きさ1の集中荷重(単位荷重)を
梁の左端から右端まで動かしてみたとき、
着目点の反力や断面力やたわみなどがどのように変化するかを
単位荷重の位置($\zeta$)の関数として表したものである。
その際、着目点を表す座標($z$)と単位荷重の位置を表す座標($\zeta$)とを
区別しないと混乱しやすいので、
このテキストでは、着目点の座標は$z$で表し、
単位荷重の位置は$\zeta$で表すことにする。
影響線というのは、大きさ1の集中荷重(単位荷重)を
梁の左端から右端まで動かしてみたとき、
着目点の反力や断面力やたわみなどがどのように変化するかを
単位荷重の位置($\zeta$)の関数として表したものである。
その際、着目点を表す座標($z$)と単位荷重の位置を表す座標($\zeta$)とを
区別しないと混乱しやすいので、
このテキストでは、着目点の座標は$z$で表し、
単位荷重の位置は$\zeta$で表すことにする。
 図のような単純梁について、両端の反力の影響線と
中央($z=\frac{\ell }{2}$)の曲げモーメントとたわみの影響線を求めてみる。
図のような単純梁について、両端の反力の影響線と
中央($z=\frac{\ell }{2}$)の曲げモーメントとたわみの影響線を求めてみる。
まずは、単位荷重の位置を表す$\zeta$が定数だと考えて、
普通に反力や断面力、たわみを$z$の関数として求める。
この問題は、
静定梁のたわみの練習問題-問4
で、$a=\zeta$, $P=1$と置いたものと同じだから、
$V_{B}(\zeta)=\frac{\zeta}{\ell }$
$V_{A}(\zeta)=\frac{\ell -\zeta}{\ell }$
便宜上、$0<z<\zeta$の領域の断面力やたわみに添字$\ _{左}$を、
$\zeta<z<\ell $の領域の断面力やたわみに添字$\ _{右}$を
つけて表すことにすると、
$0<z<\zeta$について、
$M_{左}(z,\zeta)=\frac{\ell -\zeta}{\ell }z$
$v_{左}(z,\zeta)=\frac{\zeta-\ell }{6\ell EI}\{z^{3}+(\zeta^{2}-2\ell \zeta)z\}$
$\zeta<z<\ell $について、
$M_{右}(z,\zeta)=\frac{\zeta}{\ell }(\ell -z)$
$v_{右}(z,\zeta)=\frac{\zeta}{6\ell EI}\{(z^{3}-3\ell z^{2})+(2\ell^{2}+\zeta^{2})z-\zeta^{2}\ell \}$
が普通の梁の断面力やたわみを解く要領で得られる。
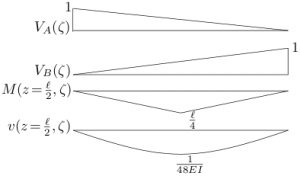
まず両端の反力の影響線は
$V_{A}(\zeta)$と$V_{B}(\zeta)$
を$\zeta$の関数として横軸に$\zeta$をとって
グラフを描けばいい。
中央($z=\frac{\ell }{2}$)の曲げモーメントやたわみの影響線を描く場合は
ちょっと注意が必要である。
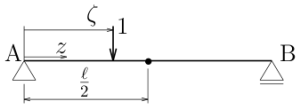 $0<\zeta<\frac{\ell }{2}$の場合
$0<\zeta<\frac{\ell }{2}$の場合
単位荷重が着目点の$z=\frac{\ell }{2}$よりも左側にある場合
(つまり着目点が単位荷重よりも右側にある場合ということだから)、
着目点の曲げモーメントやたわみを表す式は、
$\zeta<z<\ell $の場合の式つまり$M_{右}(z,\zeta)$や
$v_{右}(z,\zeta)$になる。
よって中央($z=\frac{\ell }{2}$)の曲げモーメントの影響線は、
$M_{右}(z=\frac{\ell }{2},\zeta)=\frac{\zeta}{2}
\;\;\;\;(0<\zeta<\frac{\ell }{2})$
たわみの影響線は、
$v_{右}(z=\frac{\ell }{2},\zeta)=
\frac{3\ell^{2}\zeta-4\zeta^{3}}{48EI}
\;\;\;\;(0<\zeta<\frac{\ell }{2})$
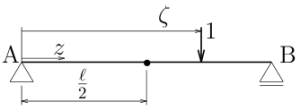 $\frac{\ell }{2}<\zeta<\ell $の場合
$\frac{\ell }{2}<\zeta<\ell $の場合
単位荷重が着目点の$z=\frac{\ell }{2}$よりも右側にある場合
(つまり着目点が単位荷重よりも左側にある場合ということだから)、
着目点の曲げモーメントやたわみを表す式は、
$0<z<\zeta$の場合の式つまり$M_{左}(z,\zeta)$や
$v_{左}(z,\zeta)$になる。
よって中央($z=\frac{\ell }{2}$)の曲げモーメントの影響線は、
$M_{左}(z=\frac{\ell }{2},\zeta)=\frac{\ell -\zeta}{2}
\;\;\;\;(\frac{\ell }{2}<\zeta<\ell )$
たわみの影響線は、
$v_{左}(z=\frac{\ell }{2},\zeta)=
\frac{4\zeta^{3}-12\ell \zeta^{2}+9\ell^{2}\zeta-\ell^{3}}{48EI}
\;\;\;\;(\frac{\ell }{2}<\zeta<\ell )$
メモ: