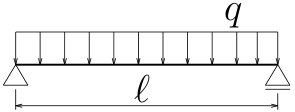
 図の片持ち梁のたわみを座標($z$)の関数として求めよ。
曲げ剛性は$EI$としてよい。
図の片持ち梁のたわみを座標($z$)の関数として求めよ。
曲げ剛性は$EI$としてよい。
注意: このページの数式は、 MathJaxを使って書いてます。 数式部分がおかしい場合は、更新ボタンをクリックすると 改善するかも知れません。 太文字のギリシャ文字($\mathbf{\sigma}$など)が、 太文字になっていない($\sigma$)かもしれません。 印刷版で確認して下さい。 その他、おかしい記述があると思ったら、 メールなどで指摘して下さい。
 図の片持ち梁のたわみを座標($z$)の関数として求めよ。
曲げ剛性は$EI$としてよい。
図の片持ち梁のたわみを座標($z$)の関数として求めよ。
曲げ剛性は$EI$としてよい。
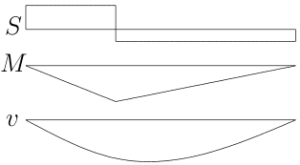
$M=\frac{q}{2}(\ell z-z^{2})$
$M=-EIv''$より
$EIv''=\frac{q}{2}(z^{2}-\ell z)$
$EIv'=\frac{q}{2}(\frac{z^{3}}{3}-\frac{\ell }{2}z^{2})+A$
$EIv=\frac{q}{2}(\frac{z^{4}}{12}-\frac{\ell }{6}z^{3})+Az+B$
境界条件:$v(0)=0, v(\ell )=0$より
${\displaystyle B=0,\ \ \
A=\frac{q\ell^{3}}{24}}$
${\displaystyle v=\frac{q}{24EI}(z^{4}-2\ell z^{3}+\ell^{3}z)}$
中央のたわみ: ${\displaystyle v\left(\frac{\ell }{2}\right)=\frac{5q\ell^{4}}{384EI}}$
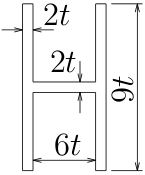 また、この梁が図のような2軸対称のH型断面をしている場合、
直応力と曲げモーメントの関係を用いて、直応力の最大値と、
それが発生する場所$(y, z)$を求めよ。
また、この梁が図のような2軸対称のH型断面をしている場合、
直応力と曲げモーメントの関係を用いて、直応力の最大値と、
それが発生する場所$(y, z)$を求めよ。
$I=\frac{2t(9t)^{3}}{12}\times 2 +\frac{6t(2t)^{3}}{12}=247t^{4}$
$M$-図より$M_{max}=M(\frac{\ell }{2})=\frac{q\ell^{2}}{8}$
$\sigma_{zz}=\frac{M}{I}y$より
$\sigma_{zz}(y=-\frac{9}{2}t, z=\frac{\ell }{2})
=\frac{\frac{q\ell^{2}}{8}}{247t^{4}}(-\frac{9}{2}t)
=-\frac{9q\ell^{2}}{3952t^{3}}$
$\sigma_{zz}(y=\frac{9}{2}t, z=\frac{\ell }{2})
=\frac{9q\ell^{2}}{3952t^{3}}$
中央のたわみを単位荷重法で求めてみる。
$M=\frac{q}{2}(\ell z-z^{2})$
左右対称なので、$0\le z\le \frac{\ell }{2}$の左半分の
$\bar{M}_{左}=\frac{z}{2}$を用いて、
左半分の積分を2倍する。
$EIv(\frac{\ell }{2})=\int_{0}^{\ell }M\bar{M}dz$
$=2\int_{0}^{\frac{\ell }{2}}M\bar{M}dz$
$=\frac{q}{2}\int_{0}^{\frac{\ell }{2}}(\ell z^{2}-z^{3})dz$
$=\frac{q}{2}[\ell \frac{z^{3}}{3}-\frac{z^{4}}{4}]_{0}^{\frac{\ell }{2}}$
$=\frac{5q\ell^{4}}{384}$
$\therefore v(\frac{\ell }{2})=\frac{5q\ell^{4}}{384EI}$
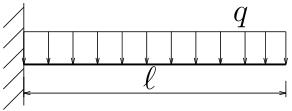 図の片持ち梁のたわみを座標($z$)の関数として求めよ。
曲げ剛性は$EI$としてよい。
図の片持ち梁のたわみを座標($z$)の関数として求めよ。
曲げ剛性は$EI$としてよい。
$M=-\frac{q}{2}(z-\ell )^{2}$
$M=-EIv''$より
$EIv''=\frac{q}{2}(z^{2}-2\ell z+\ell^{2})$
$EIv'=\frac{q}{2}(\frac{z^{3}}{3}-\ell z^{2}+\ell^{2}z)+A$
$EIv=\frac{q}{2}(\frac{z^{4}}{12}-\frac{\ell }{3}z^{3}+\frac{\ell^{2}}{2}z^{2})
+Az+B$
境界条件: $v'(0)=0, v(0)=0$より
$A=0, B=0$
$v=\frac{q}{24EI}(z^{4}-4\ell z^{3}+6\ell^{2}z^{2})$
先端のたわみ: $v(\ell )=\frac{q\ell^{4}}{8EI}$
先端のたわみを単位荷重法で求めてみる。
$M=-\frac{q}{2}(z-\ell )^{2}$
$\bar{M}=z-\ell $
$EIv(\ell )=\int_{0}^{\ell }M\bar{M}dz$
$=-\int_{0}^{\ell }\frac{q}{2}(z-\ell )^{3}dz$
$=-\frac{q}{2}[\frac{(z-\ell )^{4}}{4}]_{0}^{\ell }$
$=\frac{q\ell^{4}}{8}$
$\therefore v(\ell )=\frac{q\ell^{4}}{8EI}$
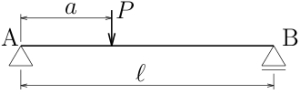 図の単純梁のたわみを座標($z$)の関数として求めよ。
曲げ剛性は$EI$としてよい。
図の単純梁のたわみを座標($z$)の関数として求めよ。
曲げ剛性は$EI$としてよい。
鉛直方向の力のつりあい: $-V_{A}+P-V_{B}=0$
A点左回りのモーメントのつりあい: $-aP+\ell V_{B}=0$
$V_{B}=\frac{a}{\ell }P$
$V_{A}=\frac{\ell -a}{\ell }P$
便宜上、$0<z<a$の領域の断面力やたわみに添字$\ _{左}$を、
$a<z<\ell $の領域の断面力やたわみに添字$\ _{右}$を
つけて表すことにすると、
$0<z<a$について、断面を切ってつりあいを考えると
$S_{左}=\frac{\ell -a}{\ell }P$
$M_{左}=\frac{\ell -a}{\ell }Pz$
$a<z<\ell $について、断面を切ってつりあいを考えると
$S_{右}=-\frac{a}{\ell }P$
$M_{右}=\frac{a}{\ell }P(\ell -z)$
$M=-EIv''$より
$0<z<a$について
$EIv_{左}''=\frac{a-\ell }{\ell }Pz$
$EIv_{左}'=\frac{a-\ell }{2\ell }Pz^{2}+A$
$EIv_{左}=\frac{a-\ell }{6\ell }Pz^{3}+Az+B$
$a<z<\ell $について
$EIv_{右}''=\frac{a}{\ell }P(z-\ell )$
$EIv_{右}'=\frac{a}{\ell }P(\frac{z^{2}}{2}-\ell z)+C$
$EIv_{右}=\frac{a}{\ell }P(\frac{z^{3}}{6}-\frac{\ell }{2}z^{2})+Cz+D$
境界条件は両端でたわみが$0$, つまり
$v_{左}(0)=0, v_{右}(\ell )=0$
これらより
$B=0$
$D=\frac{a\ell^{2}P}{3}-C\ell $
$EIv_{右}=\frac{a}{\ell }P(\frac{z^{3}}{6}-\frac{\ell }{2}z^{2})+Cz+\frac{a\ell^{2}P}{3}-C\ell $
連続条件は、$z=a$でたわみとたわみ角がそれぞれ連続、つまり
$v_{左}(a)=v_{右}(a)$
$v_{左}'(a)=v_{右}'(a)$
これらより
$C=\frac{Pa}{6\ell }(2\ell^{2}+a^{2})$
$A=\frac{Pa}{6\ell }(a-\ell )(a-2\ell )$
よって、たわみは、
$v_{左}=\frac{P(a-\ell )}{6\ell EI}\{z^{3}+(a^{2}-2\ell a)z\}
\;\;\;\;
(0<z<a)$
$v_{右}=\frac{Pa}{6\ell EI}\{(z^{3}-3\ell z^{2})+(2\ell^{2}+a^{2})z-a^{2}\ell \}
\;\;\;\;
(a<z<\ell )$
メモ: