
構造力学(基礎)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
 今回は、間接荷重とか間接載荷と呼ばれるモデルをやってみる。
橋梁では、
車などの荷重が、
荷重に抵抗する主構造(主桁とか)に直接 載荷されるのではなく、
主桁の上に間隔を空けて横桁を並べ、その上に縦桁を並べて、
まずは縦桁が荷重を受けて、それを横桁、主桁へと伝達する構造に
なっていることも多い。特にトラス橋などでは、
そういう構造になっている。
図の単純梁の上に並んでいる $\text{I}$ の形が、横桁を表していて、
イメージとしては、$\text{I}$型断面の桁みたいなものだ。
その上に $\text{I}$ と $\text{I}$ の間に 一枚ずつ板みたいなのが渡してあるが、
これが縦桁に相当する。
間接荷重のモデルとしては、単純梁の上に$\text{I}$桁が並んでいて、その上に
板が渡してあるというイメージでいいが、
実際の縦桁は、板ではなく、$\text{I}$型断面とかの桁である。
実際の
トラス橋などで、縦桁や横桁がどんな形状や配置になっていて、
それらを介して荷重が格点にどのように伝達されるか
というイメージは、
トラス橋 縦桁 横桁 格点とかで画像検索してみてほしい。
ちなみに、今までやってきた梁のように、縦桁や横桁がなく、
梁に直接 荷重が載荷されることを直接荷重とか直接載荷という。
今回は、間接荷重とか間接載荷と呼ばれるモデルをやってみる。
橋梁では、
車などの荷重が、
荷重に抵抗する主構造(主桁とか)に直接 載荷されるのではなく、
主桁の上に間隔を空けて横桁を並べ、その上に縦桁を並べて、
まずは縦桁が荷重を受けて、それを横桁、主桁へと伝達する構造に
なっていることも多い。特にトラス橋などでは、
そういう構造になっている。
図の単純梁の上に並んでいる $\text{I}$ の形が、横桁を表していて、
イメージとしては、$\text{I}$型断面の桁みたいなものだ。
その上に $\text{I}$ と $\text{I}$ の間に 一枚ずつ板みたいなのが渡してあるが、
これが縦桁に相当する。
間接荷重のモデルとしては、単純梁の上に$\text{I}$桁が並んでいて、その上に
板が渡してあるというイメージでいいが、
実際の縦桁は、板ではなく、$\text{I}$型断面とかの桁である。
実際の
トラス橋などで、縦桁や横桁がどんな形状や配置になっていて、
それらを介して荷重が格点にどのように伝達されるか
というイメージは、
トラス橋 縦桁 横桁 格点とかで画像検索してみてほしい。
ちなみに、今までやってきた梁のように、縦桁や横桁がなく、
梁に直接 荷重が載荷されることを直接荷重とか直接載荷という。
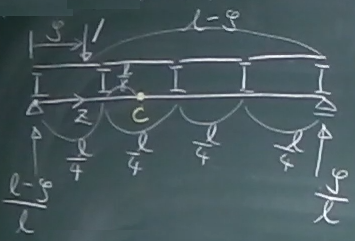
 今回は、図のような長さ$\ell$の単純梁に、$\frac{\ell}{4}$ずつの
間隔で横桁が並んでいて、横桁に長さ$\frac{\ell}{4}$の縦桁が渡してある
梁の影響線を考える。
縦桁は横桁の上にのっているだけというモデルだが、
長さ$\ell$の単純梁の上に、長さ$\frac{\ell}{4}$の単純梁が並んでいると
考えてもよい。
縦桁に載荷された荷重は、縦桁の両端の横桁からしか、下の梁に伝達されない。
例えば、縦桁の上を荷重が左端から右端へと移動していく場合、
左端から1つ目の縦桁に荷重が載っている間は、左端から1つ目と2つ目の
横桁にしか荷重はかからず、
左端から2つ目の縦桁に荷重が載っている間は、左端から2つ目と3つ目の
横桁にしか荷重はかからず、、、といった具合である。
このように荷重がある縦桁から隣の縦桁に移るごとに荷重の状態が変わるため、
1つの縦桁の間隔
(この例では、
$0\le z\le\frac{\ell}{4}$,
$\frac{\ell}{4}\le z\le\frac{2\ell}{4}$,
$\frac{2\ell}{4}\le z\le\frac{3\ell}{4}$,
$\frac{3\ell}{4}\le z\le\frac{4\ell}{4}$)
のことを、
この授業では、間接荷重区間と呼ぶことにする。
さて、
例えば左端から2つめの間接荷重区間の真ん中($z=\frac{\ell}{4}+\frac{\ell}{8}
=\frac{3}{8}\ell$)を着目点Cとして、点Cの曲げモーメントの影響線を求めてみる。
なお、今回は曲げモーメントの影響線しか求めないが、
せん断力の影響線も以下に示す同様のやり方で求められる。
今回は、図のような長さ$\ell$の単純梁に、$\frac{\ell}{4}$ずつの
間隔で横桁が並んでいて、横桁に長さ$\frac{\ell}{4}$の縦桁が渡してある
梁の影響線を考える。
縦桁は横桁の上にのっているだけというモデルだが、
長さ$\ell$の単純梁の上に、長さ$\frac{\ell}{4}$の単純梁が並んでいると
考えてもよい。
縦桁に載荷された荷重は、縦桁の両端の横桁からしか、下の梁に伝達されない。
例えば、縦桁の上を荷重が左端から右端へと移動していく場合、
左端から1つ目の縦桁に荷重が載っている間は、左端から1つ目と2つ目の
横桁にしか荷重はかからず、
左端から2つ目の縦桁に荷重が載っている間は、左端から2つ目と3つ目の
横桁にしか荷重はかからず、、、といった具合である。
このように荷重がある縦桁から隣の縦桁に移るごとに荷重の状態が変わるため、
1つの縦桁の間隔
(この例では、
$0\le z\le\frac{\ell}{4}$,
$\frac{\ell}{4}\le z\le\frac{2\ell}{4}$,
$\frac{2\ell}{4}\le z\le\frac{3\ell}{4}$,
$\frac{3\ell}{4}\le z\le\frac{4\ell}{4}$)
のことを、
この授業では、間接荷重区間と呼ぶことにする。
さて、
例えば左端から2つめの間接荷重区間の真ん中($z=\frac{\ell}{4}+\frac{\ell}{8}
=\frac{3}{8}\ell$)を着目点Cとして、点Cの曲げモーメントの影響線を求めてみる。
なお、今回は曲げモーメントの影響線しか求めないが、
せん断力の影響線も以下に示す同様のやり方で求められる。
まずは、反力を求めるが、 反力の公式を 使えば、左端が$\frac{\ell-\zeta}{\ell}$, 右端が$\frac{\zeta}{\ell}$となる。 もちろん、公式を覚えてなくても力のつりあいから求めればよい。
上述したように、間接荷重では、荷重がある間接荷重区間から隣の間接荷重区間に
乗り移る度に荷重の状態が変わるので、
1)荷重が着目点のある間接荷重区間よりも左側の間接荷重区間にある場合
2)荷重が着目点のある間接荷重区間にある場合
3)荷重が着目点のある間接荷重区間よりも右側の間接荷重区間にある場合
の3つの場合に場合分けする。
今回の場合だと、以下のようになる。
1) $0\le \zeta\le\frac{\ell}{4}$
2) $\frac{\ell}{4}\le \zeta\le\frac{\ell}{2}$
3) $\frac{\ell}{2}\le \zeta\le\ell$
着目点が左から一番目の間接荷重区間にある場合は、上記の1)の場合はなくなるし、
着目点が一番右側の間接荷重区間にある場合は、上記の3)の場合はなくなる。
 荷重が左から一番目の間接荷重区間($0\le z \le \frac{\ell}{4}$)
にある場合、つまり$\zeta$が$0\le \zeta \le \frac{\ell}{4}$となっているときの
着目点C($z=\frac{3}{8}\ell$)での曲げモーメントの影響線関数$M_{C}(\zeta)$を求める。
着目点Cで梁を切断すべきだから、まずは
点Cで梁を切断し、梁を2つの
ピースに分ける。
その際、
左側のピースは、荷重の載っている間接荷重区間を含むから、
荷重の載っている縦桁や横桁も含めてピースを取り出さなければいけない
(図の左側に、こちゃこちゃと小さく描いてある)。
一方、右側のピースは、点Cより右にある横桁は、どれも荷重がかかっていないから、
横桁から上は考えなくてよい。
左側のピースか右側のピースどちらかを取り出して力のつりあいを考えればよいが、
今回は、
横桁から上を考えなくてよい右側を取り出す。
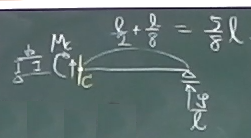
点Cから右端までの長さは、$\frac{\ell}{8}+\frac{\ell}{2}=\frac{5}{8}\ell$である。
点C回りのモーメントのつりあいから、
荷重が左から一番目の間接荷重区間($0\le z \le \frac{\ell}{4}$)
にある場合、つまり$\zeta$が$0\le \zeta \le \frac{\ell}{4}$となっているときの
着目点C($z=\frac{3}{8}\ell$)での曲げモーメントの影響線関数$M_{C}(\zeta)$を求める。
着目点Cで梁を切断すべきだから、まずは
点Cで梁を切断し、梁を2つの
ピースに分ける。
その際、
左側のピースは、荷重の載っている間接荷重区間を含むから、
荷重の載っている縦桁や横桁も含めてピースを取り出さなければいけない
(図の左側に、こちゃこちゃと小さく描いてある)。
一方、右側のピースは、点Cより右にある横桁は、どれも荷重がかかっていないから、
横桁から上は考えなくてよい。
左側のピースか右側のピースどちらかを取り出して力のつりあいを考えればよいが、
今回は、
横桁から上を考えなくてよい右側を取り出す。
点Cから右端までの長さは、$\frac{\ell}{8}+\frac{\ell}{2}=\frac{5}{8}\ell$である。
点C回りのモーメントのつりあいから、
$\sum_{C}\circlearrowleft=-M_{C}+\frac{\zeta}{\ell}\cdot\frac{5}{8}\ell=0$ よって、
$M_{C}(\zeta)=\frac{5}{8}\zeta\;\;\;\;(0\le\zeta\le\frac{\ell}{4})$
 次に、左から2つ目の間接荷重区間
($\frac{\ell}{4}\le z\le\frac{\ell}{2}$)
に荷重がある場合、つまり、
$\frac{\ell}{4}\le \zeta\le\frac{\ell}{2}$の場合を考える。
この場合、荷重のある間接荷重区間内に着目点Cがあるから、
点Cで梁を2つのピースに切り離したときに、
左側のピースの横桁にも右側のピースの横桁にも荷重が分配されてしまう。
どちらのピースを取り出しても荷重の分配を考えざるを得ないので、
そういう場合は、ゲルバー梁と同じ要領で
上に載っている縦桁から考えていく。
縦桁部分は、単純梁として、下の梁から切り離して考えればよい。
縦桁
($\frac{\ell}{4}\le z\le\frac{\ell}{2}$)
の左端($z=\frac{\ell}{4}$)から
単位荷重の載荷位置($z=\zeta$)までの
長さは$\zeta-\frac{\ell}{4}$だし、
単位荷重の載荷位置($z=\zeta$)から
縦桁の右端($z=\frac{\ell}{2}$)までの
長さは$\frac{\ell}{2}-\zeta$だから、
この縦桁の両端の反力は、
反力の公式から、
次に、左から2つ目の間接荷重区間
($\frac{\ell}{4}\le z\le\frac{\ell}{2}$)
に荷重がある場合、つまり、
$\frac{\ell}{4}\le \zeta\le\frac{\ell}{2}$の場合を考える。
この場合、荷重のある間接荷重区間内に着目点Cがあるから、
点Cで梁を2つのピースに切り離したときに、
左側のピースの横桁にも右側のピースの横桁にも荷重が分配されてしまう。
どちらのピースを取り出しても荷重の分配を考えざるを得ないので、
そういう場合は、ゲルバー梁と同じ要領で
上に載っている縦桁から考えていく。
縦桁部分は、単純梁として、下の梁から切り離して考えればよい。
縦桁
($\frac{\ell}{4}\le z\le\frac{\ell}{2}$)
の左端($z=\frac{\ell}{4}$)から
単位荷重の載荷位置($z=\zeta$)までの
長さは$\zeta-\frac{\ell}{4}$だし、
単位荷重の載荷位置($z=\zeta$)から
縦桁の右端($z=\frac{\ell}{2}$)までの
長さは$\frac{\ell}{2}-\zeta$だから、
この縦桁の両端の反力は、
反力の公式から、
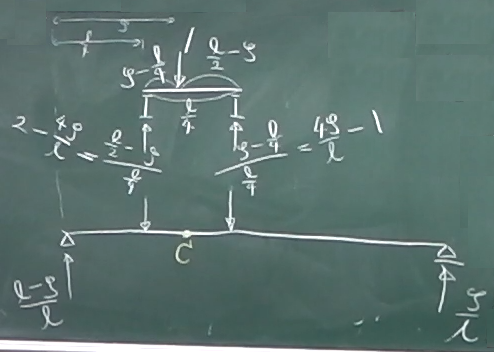
左端では$\frac{\frac{\ell}{2}-\zeta}{\frac{\ell}{4}}\cdot 1=2-\frac{4\zeta}{\ell}$
右端では$\frac{\zeta-\frac{\ell}{4}}{\frac{\ell}{4}}\cdot 1=\frac{4\zeta}{\ell}-1$
これらの反力が作用・反作用の関係で、下の梁の横桁の位置に載荷されている
と考えて、下の梁を解けばよい。
とういことで、これらの反力を下の梁の横桁の位置に載荷した状態で、
下の梁の点Cを切断し、2つのピースに切り離す。
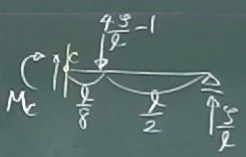 どちらかのピースを取り出して力のつりあいを考えればよいが、
今回は右側のピースを取り出す。
点C($z=\frac{3}{8}\ell$)から横桁のある載荷点($z=\frac{\ell}{2}$)
までの長さは、$\frac{\ell}{8}$である。
載荷点から右端までの長さは$\frac{\ell}{2}$である。
点C回りのモーメントのつりあいから、
どちらかのピースを取り出して力のつりあいを考えればよいが、
今回は右側のピースを取り出す。
点C($z=\frac{3}{8}\ell$)から横桁のある載荷点($z=\frac{\ell}{2}$)
までの長さは、$\frac{\ell}{8}$である。
載荷点から右端までの長さは$\frac{\ell}{2}$である。
点C回りのモーメントのつりあいから、
$\sum_{C}\circlearrowleft=-M_{C}
-(\frac{4\zeta}{\ell}-1)\cdot\frac{\ell}{8}+\frac{\zeta}{\ell}
(\frac{\ell}{8}+\frac{\ell}{2})=0$
よって、
$M_{C}(\zeta)=\frac{\zeta+\ell}{8}\;\;\;\;
(\frac{\ell}{4}\le\zeta\le\frac{\ell}{2})$
 荷重が着目点Cのある間接荷重区間よりも右側($\frac{\ell}{2}\ell\le z \le \ell$)の
間接荷重区間にある場合、
つまり$\zeta$が$\frac{\ell}{2}\le \zeta \le \ell$となっているときの
着目点C($z=\frac{3}{8}\ell$)での曲げモーメントの影響線関数$M_{C}(\zeta)$を
求める。
着目点Cで梁を切断すべきだから、まずは
点Cで梁を切断し、梁を2つの
ピースに分ける。
その際、
右側のピースは、荷重の載っている間接荷重区間を含むから、
荷重の載っている縦桁や横桁も含めてピースを取り出さなければいけない
(図の右側に、こちゃこちゃと描いてある)。
一方、左側のピースは、点Cより左にある横桁は、どれも荷重がかかっていないから、
横桁から上は考えなくてよい。
左側のピースか右側のピースどちらかを取り出して力のつりあいを考えればよいが、
今回は、
横桁から上を考えなくてよい左側を取り出す。
左端から
点Cまでの長さは、
$\frac{\ell}{4}+\frac{\ell}{8}=\frac{3}{8}\ell$である。
点C回りのモーメントのつりあいから、
荷重が着目点Cのある間接荷重区間よりも右側($\frac{\ell}{2}\ell\le z \le \ell$)の
間接荷重区間にある場合、
つまり$\zeta$が$\frac{\ell}{2}\le \zeta \le \ell$となっているときの
着目点C($z=\frac{3}{8}\ell$)での曲げモーメントの影響線関数$M_{C}(\zeta)$を
求める。
着目点Cで梁を切断すべきだから、まずは
点Cで梁を切断し、梁を2つの
ピースに分ける。
その際、
右側のピースは、荷重の載っている間接荷重区間を含むから、
荷重の載っている縦桁や横桁も含めてピースを取り出さなければいけない
(図の右側に、こちゃこちゃと描いてある)。
一方、左側のピースは、点Cより左にある横桁は、どれも荷重がかかっていないから、
横桁から上は考えなくてよい。
左側のピースか右側のピースどちらかを取り出して力のつりあいを考えればよいが、
今回は、
横桁から上を考えなくてよい左側を取り出す。
左端から
点Cまでの長さは、
$\frac{\ell}{4}+\frac{\ell}{8}=\frac{3}{8}\ell$である。
点C回りのモーメントのつりあいから、
$\sum_{C}\circlearrowleft=-\frac{\ell-\zeta}{\ell}\cdot \frac{3}{8}\ell
+M_{C}=0$ よって、
$M_{C}(\zeta)=\frac{3}{8}(\ell-\zeta)\;\;\;\;(\frac{\ell}{2}\le\zeta\le\ell)$
求めた影響線関数を間接荷重区間ごとに整理して、
それぞれの区間の両端の値を求める。
$
M_{C}(\zeta)=
\begin{cases}
\frac{5}{8}\zeta & \;\;\;\;(0\le\zeta\le\frac{\ell}{4})
\;\;\;\; M_{C}(0)=0,\; M_{C}(\frac{\ell}{4})=\frac{5}{32}\ell
\\
\frac{\zeta+\ell}{8} & \;\;\;\;
(\frac{\ell}{4}\le\zeta\le\frac{\ell}{2})
\;\;\;\; M_{C}(\frac{\ell}{4})=\frac{5}{32}\ell,\;
M_{C}(\frac{\ell}{2})=\frac{3}{16}\ell
\\
\frac{3}{8}(\ell-\zeta) & \;\;\;\;(\frac{\ell}{2}\le\zeta\le\ell)
\;\;\;\; M_{C}(\frac{\ell}{2})=\frac{3}{16}\ell,\;
M_{C}(\ell)=0
\\
\end{cases}
$
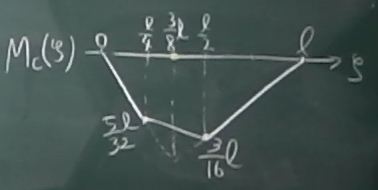 影響線関数は、どの区間でも$\zeta$の1次式で直線だから、
各区間の両端の値を直線で結べばよい。
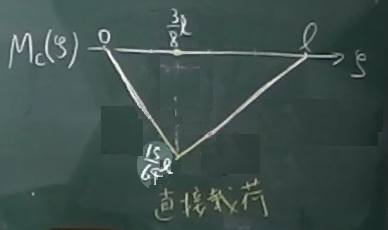
すると、図のようになる。
ちなみに、間接荷重の影響線は、
点Cに直接載荷されている梁の影響線を描いて(図の点線)から、
着目点Cのある間接荷重区間($\frac{\ell}{4}$から$\frac{\ell}{2}$まで)を
直線で結ぶことで描ける。
つまり、影響線を描けさえすればいいのであれば、
上の手順2$\sim$手順6のめんどくさいことをせずに、
直接荷重の影響線を求め、着目点を含む間接荷重区間を直線で結べばよい。
影響線関数は、どの区間でも$\zeta$の1次式で直線だから、
各区間の両端の値を直線で結べばよい。
すると、図のようになる。
ちなみに、間接荷重の影響線は、
点Cに直接載荷されている梁の影響線を描いて(図の点線)から、
着目点Cのある間接荷重区間($\frac{\ell}{4}$から$\frac{\ell}{2}$まで)を
直線で結ぶことで描ける。
つまり、影響線を描けさえすればいいのであれば、
上の手順2$\sim$手順6のめんどくさいことをせずに、
直接荷重の影響線を求め、着目点を含む間接荷重区間を直線で結べばよい。
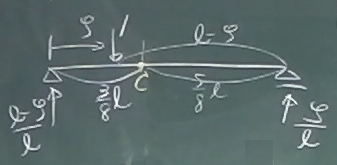 では、直接荷重の影響線を描いてから間接荷重区間を直線で結ぶ方法でも、
同じ影響線が描けることを確認してみる。
図のように、直接載荷されている単純梁について、
着目点C($z=\frac{3}{8}\ell$)での曲げモーメントの影響線$M_{C}^{直}(\zeta)$
を求めてみる。
では、直接荷重の影響線を描いてから間接荷重区間を直線で結ぶ方法でも、
同じ影響線が描けることを確認してみる。
図のように、直接載荷されている単純梁について、
着目点C($z=\frac{3}{8}\ell$)での曲げモーメントの影響線$M_{C}^{直}(\zeta)$
を求めてみる。
単位荷重が着目点Cより左にある場合
$(0\le\zeta\le\frac{3}{8}\ell)$
着目点C($z=\frac{3}{8}\ell$)で梁を切断し、左側と右側の2つのピースに切り離す。
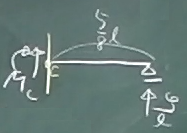 左側か右側かどちらかのピースを取り出して力のつりあいを考えればよいが、
今回は、単位荷重を含まない右側のピースを取り出す。
点C回りのモーメントのつりあいから、
左側か右側かどちらかのピースを取り出して力のつりあいを考えればよいが、
今回は、単位荷重を含まない右側のピースを取り出す。
点C回りのモーメントのつりあいから、
$\sum_{C}\circlearrowleft=-M_{C}^{直}+\frac{\zeta}{\ell}\cdot\frac{5}{8}\ell=0$ よって、
$M_{C}^{直}(\zeta)=\frac{5}{8}\zeta\;\;\;\;(0\le\zeta\le\frac{3}{8}\ell)$
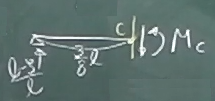 単位荷重が着目点Cより右にある場合
$(\frac{3}{8}\ell\le\zeta\le\ell)$
単位荷重が着目点Cより右にある場合
$(\frac{3}{8}\ell\le\zeta\le\ell)$
着目点C($z=\frac{3}{8}\ell$)で梁を切断し、左側と右側の2つのピースに切り離す。
左側か右側かどちらかのピースを取り出して力のつりあいを考えればよいが、
今回は、単位荷重を含まない左側のピースを取り出す。
点C回りのモーメントのつりあいから、
$\sum_{C}^{直}\circlearrowleft=-\frac{\ell-\zeta}{\ell}\cdot \frac{3}{8}\ell
+M_{C}^{直}=0$ よって、
$M_{C}^{直}(\zeta)=\frac{3}{8}(\ell-\zeta)\;\;\;\;(\frac{3}{8}\ell\le\zeta\le\ell)$
 以上を整理して、領域の境界の値を求める。
以上を整理して、領域の境界の値を求める。
$M_{C}^{直}(\zeta)=
\begin{cases}
\frac{5}{8}\zeta &\;\;\;\;(0\le\zeta\le\frac{3}{8}\ell)
\;\;\;\; M_{C}^{直}(0)=0,\; M_{C}^{直}(\frac{3}{8}\ell)=\frac{15}{64}\ell\\
\frac{3}{8}(\ell-\zeta) &\;\;\;\;(\frac{3}{8}\ell\le\zeta\le\ell)
\;\;\;\; M_{C}^{直}(\frac{3}{8}\ell)=\frac{15}{64}\ell,\;
M_{C}^{直}(\ell)=0
\end{cases}
$
影響線関数はどちらの領域でも$\zeta$の1次式で直線だから、
各領域の両端の値を結べば、図のように直接載荷の場合の影響線が描ける。
 次に、着目点Cがある間接荷重区間($\frac{\ell}{4}\le \zeta \le \frac{\ell}{2}$)の両端での影響線の値を求める。
次に、着目点Cがある間接荷重区間($\frac{\ell}{4}\le \zeta \le \frac{\ell}{2}$)の両端での影響線の値を求める。
$M_{C}^{直}(\frac{\ell}{4})=
\frac{5}{8}\cdot\frac{\ell}{4}=\frac{5}{32}\ell$
$M_{C}^{直}(\frac{\ell}{2})=
\frac{3}{8}(\ell-\frac{\ell}{2})=\frac{3}{16}\ell$
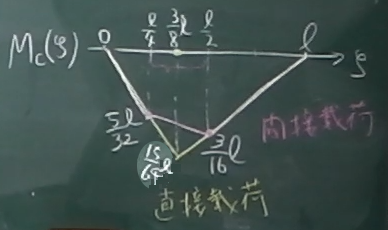 着目点Cのある間接荷重区間の両端での直接載荷の$M_{C}^{直}$の値を
図の赤線のように直線で結べば、それが間接載荷の影響線となる。
着目点Cのある間接荷重区間の両端での直接載荷の$M_{C}^{直}$の値を
図の赤線のように直線で結べば、それが間接載荷の影響線となる。
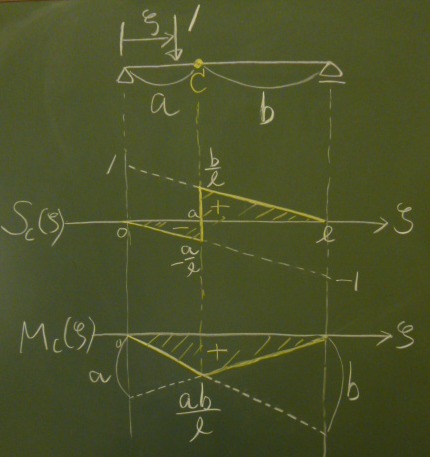 図のように、長さ$\ell$の単純梁を$a:b$の比に分ける点を着目点Cとして、
せん断力と曲げモーメントの影響線関数を求め、影響線を描いてみると、図のようになる
(各自、確かめてみよう)。
この影響線図を覚えておけば、公式のように使うことができる。
図のように、長さ$\ell$の単純梁を$a:b$の比に分ける点を着目点Cとして、
せん断力と曲げモーメントの影響線関数を求め、影響線を描いてみると、図のようになる
(各自、確かめてみよう)。
この影響線図を覚えておけば、公式のように使うことができる。
 例えば、上で影響線を求めた直接載荷の梁に、
この公式を適用するなら、
例えば、上で影響線を求めた直接載荷の梁に、
この公式を適用するなら、
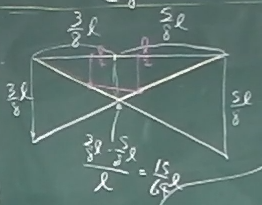 図のように、あっという間に影響線が描けてしまう。
まあ、大学院入試とか就職試験とか公務員試験の際には、こうした
公式各種を覚えておくと時間短縮になって便利ではある。が、
上でややめんどくさい方法で求めたように、
適切な場合分けをして、力のつりあいを考えさえすれば
影響線が求まるということの方がより本質的で重要なことだろう。
図のように、あっという間に影響線が描けてしまう。
まあ、大学院入試とか就職試験とか公務員試験の際には、こうした
公式各種を覚えておくと時間短縮になって便利ではある。が、
上でややめんどくさい方法で求めたように、
適切な場合分けをして、力のつりあいを考えさえすれば
影響線が求まるということの方がより本質的で重要なことだろう。
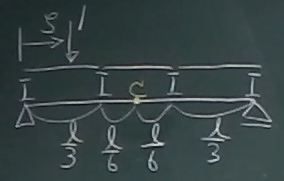 着目点Cでの曲げモーメントの影響線関数
$S_{C}(\zeta), M_{C}(\zeta)$を求め、
その影響線(下が正)を描け。
答えは、
ここ。
動画の解説は、
第14回 例題。
着目点Cでの曲げモーメントの影響線関数
$S_{C}(\zeta), M_{C}(\zeta)$を求め、
その影響線(下が正)を描け。
答えは、
ここ。
動画の解説は、
第14回 例題。
2024年度小テスト:
小テスト240726
2020年度小テスト:
問1,
問2,
問3,
問4,
解答
メモ: