
構造力学(マトリクス構造解析)目次
(授業動画)
小さい字は補足説明なので、読み飛ばしてもいいです。
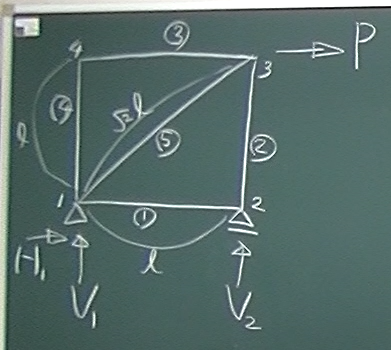 マトリクス構造解析IIの第5回(13回)で、
図のような5要素トラスをトラス要素のプログラム(torasu5.py)で解いたが、
今回は、この同じ5要素トラスを、節点を剛結として骨組のプログラム(hone5.py)で
解いて比較してみたい。
現代の一般的なトラスは、
格点部にヒンジはなく、上弦材や
下弦材から突き出した ガセットプレートと言われるプレート部分に、
トラス部材がボルトでしっかりと連結されているが、
それでも、変位や部材力はトラスモデルとして計算した結果とよく合うと考えられている
。
それを確かめてみようという趣旨である。
なので、
マトリクス構造解析IIの第5回(13回)
と同様に、ホームセンターに売っている10mm角の
1m程度の角材を想定し、第13回と同じく
マトリクス構造解析IIの第5回(13回)で、
図のような5要素トラスをトラス要素のプログラム(torasu5.py)で解いたが、
今回は、この同じ5要素トラスを、節点を剛結として骨組のプログラム(hone5.py)で
解いて比較してみたい。
現代の一般的なトラスは、
格点部にヒンジはなく、上弦材や
下弦材から突き出した ガセットプレートと言われるプレート部分に、
トラス部材がボルトでしっかりと連結されているが、
それでも、変位や部材力はトラスモデルとして計算した結果とよく合うと考えられている
。
それを確かめてみようという趣旨である。
なので、
マトリクス構造解析IIの第5回(13回)
と同様に、ホームセンターに売っている10mm角の
1m程度の角材を想定し、第13回と同じく
$E=10$GPa$=10000$N/mm$^{2}$
$A=(10$mm$)^{2}=100$mm$^{2}$
$\ell=1$m$=1000$mm
$P=500$N
とする。
まず、 hone5.pyを ダウンロードするか、 このページの末尾のソースをテキストエディタに貼り付けて保存する。 設定内容は、torasu5.pyやhone2.pyとほぼ同じだが、一応、説明する。
nyou = 5 #要素数 nset = 4 #節点数
まず、以下のように書いてあるところを見つける。
# 要素1の剛性マトリクス el = 1000.0 #1要素の長さ[mm] ea = 10.0e3 * 10.0**2 #EA, ヤング率[N/mm^2]*面積[mm^2] ei = 10.0e3 * 10.0**4 / 12.0 #EI, ヤング率[N/mm^2]*断面2次モーメント[mm^4] s[1][2][2] = ea/el s[1][2][5] = -ea/el s[1][5][2] = -ea/el s[1][5][5] = ea/el s[1][1][1] = 12.0*ei/el**3 s[1][1][3] = -6.0*ei/el**2 s[1][1][4] = -12.0*ei/el**3 s[1][1][6] = -6.0*ei/el**2 s[1][3][1] = -6.0*ei/el**2 s[1][3][3] = 4.0*ei/el s[1][3][4] = 6.0*ei/el**2 s[1][3][6] = 2.0*ei/el s[1][4][1] = -12.0*ei/el**3 s[1][4][3] = 6.0*ei/el**2 s[1][4][4] = 12.0*ei/el**3 s[1][4][6] = 6.0*ei/el**2 s[1][6][1] = -6.0*ei/el**2 s[1][6][3] = 2.0*ei/el s[1][6][4] = 6.0*ei/el**2 s[1][6][6] = 4.0*ei/el
単位は力を[N], 長さを[mm]で与えている。
$\ell=1000$mmだから el=1000.0
ヤング率は、10GPa=10kMPa=10kN/mm$^{2}=10\times 10^{3}$N/mm$^{2}$だから、10.0e3となる。
$A=(10$mm$)^{2}$だから
$EA=10\times 10^{3}$N/mm$^{2}\times(10$mm$)^{2}$ よって、ea=10.0e3*10.0e0**2
1辺10mmの正方形の断面2次モーメントは、$I=(10$mm$)^{4}/12$だから、
$EI=10\times 10^{3}$N/mm$^{2}\times(10$mm$)^{4}/12$ よって、
ei=10.0e3*10.0e0**4/12.0
#要素2から要素4までの剛性マトリクス
for k in range(2, 5):
for i in range(1, 7):
for j in range(1, 7):
s[k][i][j] = s[1][i][j]
要素②から要素④までは、要素①と同じでいいから、 要素①の剛性マトリクスを代入すればよい。 for文の説明は5要素トラスのときの説明参照。 トラスの剛性マトリクスは$4\times 4$だったが、骨組では$6\times 6$になってるから、 range(1, 7)になる。
#要素5の剛性マトリクス el = el * math.sqrt(2.0) s[5][2][2] = ea/el s[5][2][5] = -ea/el s[5][5][2] = -ea/el s[5][5][5] = ea/el s[5][1][1] = 12.0*ei/el**3 s[5][1][3] = -6.0*ei/el**2 s[5][1][4] = -12.0*ei/el**3 s[5][1][6] = -6.0*ei/el**2 s[5][3][1] = -6.0*ei/el**2 s[5][3][3] = 4.0*ei/el s[5][3][4] = 6.0*ei/el**2 s[5][3][6] = 2.0*ei/el s[5][4][1] = -12.0*ei/el**3 s[5][4][3] = 6.0*ei/el**2 s[5][4][4] = 12.0*ei/el**3 s[5][4][6] = 6.0*ei/el**2 s[5][6][1] = -6.0*ei/el**2 s[5][6][3] = 2.0*ei/el s[5][6][4] = 6.0*ei/el**2 s[5][6][6] = 4.0*ei/el
要素⑤は、$\ell=1000\sqrt{2}$mmとすればいい。
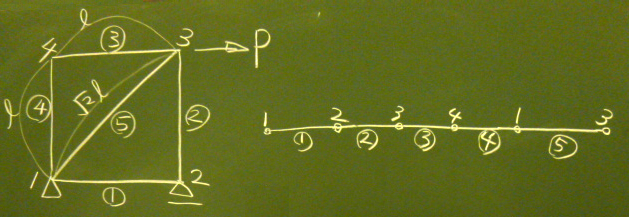 5要素トラスのときと同様に設定。
5要素トラスのときと同様に設定。
#各要素の左節点番号、右節点番号 hidari[1]=1; migi[1]=2 hidari[2]=2; migi[2]=3 hidari[3]=3; migi[3]=4 hidari[4]=4; migi[4]=1 hidari[5]=1; migi[5]=3
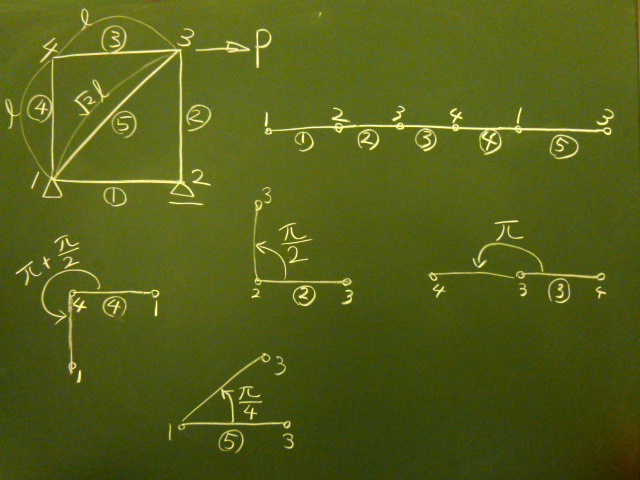 5要素トラスのときと同様に設定。
5要素トラスのときと同様に設定。
#各要素の回転角(上の左右節点番号がz軸に横たわる状態からの) th[1]=0.0 th[2]=pi/2.0 th[3]=pi th[4]=pi+pi/2.0 th[5]=pi/4.0
5要素トラスのときと同様に設定。 節点1と節点2は回転は自由だから、xt[]は拘束しない。
# 境界条件 xv[1]=0.0 xw[1]=0.0 xv[2]=0.0
5要素トラスのときと同様に設定。
# 荷重条件(y方向:fy[節点番号], z方向:fz[節点番号], モーメント外力:cx[節点番号]) fz[3]=500.0 #[N]
まずは、$\ell=1000$mmとして トラス要素のプログラム(torasu5.py)と 梁要素のプログラム(hone5.py)を実行してみる。
$ python3 torasu5.py
節点番号:1 v=0.0000000000, w=0.0000000000
節点番号:2 v=0.0000000000, w=-0.0000000000
節点番号:3 v=0.5000000000, w=1.9142135624
節点番号:4 v=0.0000000000, w=1.9142135624
部材番号: 1 S(1)= 0.0000000000, N(1)= 0.0000000000
S(2)= 0.0000000000, N(2)= -0.0000000000
部材番号: 2 S(2)=-500.0000000000, N(2)= 0.0000000000
S(3)= 500.0000000000, N(3)= -0.0000000000
部材番号: 3 S(3)= -0.0000000000, N(3)= -0.0000000000
S(4)= 0.0000000000, N(4)= 0.0000000000
部材番号: 4 S(4)= -0.0000000000, N(4)= 0.0000000000
S(1)= 0.0000000000, N(1)= 0.0000000000
部材番号: 5 S(1)= 500.0000000000, N(1)=-500.0000000000
S(3)=-500.0000000000, N(3)= 500.0000000000
$ python3 hone5.py
節点番号:1 v=0.0, w=0.0, th=-0.0009742290735677584
節点番号:2 v=0.0, w=8.329266630847247e-05, th=-0.0008683972868173793
節点番号:3 v=0.49990786868198056, w=1.9136509005161437, th=-0.0012928846027122304
節点番号:4 v=-7.681515735391396e-05, w=1.9135704243229923, th=-0.0012433879120517478
曲げモーメントの単位に注意!
部材番号: 1 S(1)= 0.0921313180, N(1)= -0.0832926663, M(1)= -46.9475905659
S(2)= -0.0921313180, N(2)= 0.0832926663, M(2)= -45.1837274534
部材番号: 2 S(2)=-499.9078686820, N(2)= -0.0832926663, M(2)= 45.1837274534
S(3)= 499.9078686820, N(3)= 0.0832926663, M(3)= 38.1089388551
部材番号: 3 S(3)= -0.0768151574, N(3)= 0.0804761932, M(3)= -38.8200510993
S(4)= 0.0768151574, N(4)= -0.0804761932, M(4)= -37.9951062550
部材番号: 4 S(4)= -0.0768151574, N(4)= 0.0804761932, M(4)= 37.9951062550
S(1)= 0.0768151574, N(1)= -0.0804761932, M(1)= 42.4810868964
部材番号: 5 S(1)= 499.8310535246, N(1)=-499.8362311405, M(1)= 4.4665036695
S(3)=-499.8310535246, N(3)= 499.8362311405, M(3)= 0.7111122442
変位については、表示桁数すべてが 手計算と一致するトラス要素が$v_{3}=0.5000000000, w_{3}=1.9142135624$に対して、 梁要素が$v_{3}=0.49990786868198056, w_{3}=1.9136509005161437$と 有効桁5桁目ぐらいからずれてきている。とはいえ、トラス要素と有効桁3桁以上が一致する。 節点力も、トラス要素は理論値通りの鉛直・水平に500Nずつとなるところが、 梁要素だと、499.8Nぐらいだ。まあ、四捨五入すればトラスモデルと有効桁3桁は一致する。 節点は剛結なので、モーメントも発生しているが、最も大きい値でも 47Nmm とかだ。 50mmの片持ち梁の先端に1N($\simeq$100gf)を載せたぐらいのモーメントだから、 500Nの荷重から考えて、大したことはない。 これなら、トラスモデルでも十分に実用的予測に使えるのではないか。
では、10mm角の部材を、断面はそのままで もっと短くして$\ell=100$mm にして解いてみる。 上がトラス要素、下が梁要素である。
$ python3 torasu5_100.py
節点番号:1 v=0.0000000000, w=0.0000000000
節点番号:2 v=0.0000000000, w=-0.0000000000
節点番号:3 v=0.0500000000, w=0.1914213562
節点番号:4 v=0.0000000000, w=0.1914213562
部材番号: 1 S(1)= 0.0000000000, N(1)= 0.0000000000
S(2)= 0.0000000000, N(2)= -0.0000000000
部材番号: 2 S(2)=-500.0000000000, N(2)= 0.0000000000
S(3)= 500.0000000000, N(3)= -0.0000000000
部材番号: 3 S(3)= 0.0000000000, N(3)= 0.0000000000
S(4)= -0.0000000000, N(4)= -0.0000000000
部材番号: 4 S(4)= 0.0000000000, N(4)= -0.0000000000
S(1)= 0.0000000000, N(1)= 0.0000000000
部材番号: 5 S(1)= 500.0000000000, N(1)=-500.0000000000
S(3)=-500.0000000000, N(3)= 500.0000000000
$ python3 hone5_100.py
節点番号:1 v=0.0, w=0.0, th=-0.0009436267529166757
節点番号:2 v=0.0, w=0.000802491377301718, th=-0.000837767415225925
節点番号:3 v=0.0491093029159287, w=0.18599711577640254, th=-0.0012611423181526494
節点番号:4 v=-0.0007380141153292914, w=0.185222619088541, th=-0.0012118322531311611
曲げモーメントの単位に注意!
部材番号: 1 S(1)= 8.9069708407, N(1)= -8.0249137730, M(1)=-454.1701535099
S(2)= -8.9069708407, N(2)= 8.0249137730, M(2)=-436.5269305614
部材番号: 2 S(2)=-491.0930291593, N(2)= -8.0249137730, M(2)= 436.5269305614
S(3)= 491.0930291593, N(3)= 8.0249137730, M(3)= 365.9644467403
部材番号: 3 S(3)= -7.3801411533, N(3)= 7.7449668786, M(3)=-373.1162297498
S(4)= 7.3801411533, N(4)= -7.7449668786, M(4)=-364.8978855795
部材番号: 4 S(4)= -7.3801411533, N(4)= 7.7449668786, M(4)= 364.8978855795
S(1)= 7.3801411533, N(1)= -7.7449668786, M(1)= 409.5988022820
部材番号: 5 S(1)= 483.7128880060, N(1)=-484.2301193484, M(1)= 44.5713512279
S(3)=-483.7128880060, N(3)= 484.2301193484, M(3)= 7.1517830095
トラス要素の方は、恐らく手計算にほぼ一致する答えが出ているのだと思うが、 実際の剛結トラスに近いであろう梁要素の結果は、やや違いが出てきた。 節点3の変位は、トラス要素が $v_{3}=0.0500000000$, $w_{3}=0.1914213562$に対して、 梁要素では、 $v_{3}=0.0491093029159287$, $w_{3}=0.18599711577640254$だから、 トラス要素に対して$2\sim 3\%$程度、小さい値となっている。 それでも$2\sim 3\%$しか違わない。 節点力も、理想的トラスモデルでは、500Nとなるところが、 484Nとかだから約3%ぐらい違っている。 それでも誤差3%程度だ。 節点のモーメントは、大きいところで454Nmmとかだが、 100mmの片持ち梁に 5N($\simeq$500gf)を載せたぐらいのモーメントだから 500N($\simeq$50kgf)の荷重から考えると、大したことはない。 このように、節点が剛結のトラスがトラスモデルとして扱えるかどうかは、 部材の細長さに関係する。 後期に鋼構造設計学の授業で「細長比」というパラメーターについて習うと思うが、 鋼構造では部材の細長さを表す細長比はとても重要である。
第5回でやった
以下の5要素トラス(自分の学籍番号のもの)を、
節点を剛結とみなして梁要素のプログラム(hone5.py)で解き、
節点変位や節点力がトラス要素(torasu5.py)で解いたものと
どれくらい変わるか考察せよ。
トラスの諸元は第5回と同じとするが、
長さ$\ell$については、短くして(torasu5.pyとhone5.pyそれぞれで)
解いたものと比較した上で、
部材の細長さと、節点が剛結のトラスをトラスモデルとして扱うことの妥当性について考察せよ。
長さ$\ell$の水平、鉛直の4本の部材が正方形を作り、
長さ$\sqrt{2}\ell$の斜材が1本入っている。
$E=10$GPa$=10000$N/mm$^{2}$
$A=(10$mm$)^{2}=100$mm$^{2}$
$\ell=200\sim 1000$mm
$P=500$N
とする。
WebClassの「プログラム課題7」から、
hone5.pyを修正したプログラム(ellは変えて計算するので)の代表的な
1つ(例えば hone5_100.py とか)と、
その出力ファイル(例えば kekka7.txt とか)を
それぞれアップロードせよ。
どうしてもエラーが取れないなどの場合は、
出力ファイルの代わりに、エラー画面等
をテキストエディタに貼り付けて保存したものをアップロードする。
また、最後のコメント欄に、
節点が剛結のトラスをトラスモデルとして扱う妥当性についての
考察を書くこと。
うまく実行できなかった場合は、
どういう症状で実行できないのかの説明を書き込むこと。
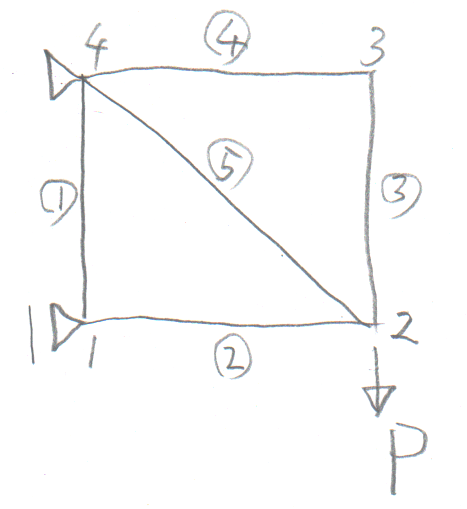 学籍番号の末尾が1か7の人。
学籍番号の末尾が1か7の人。
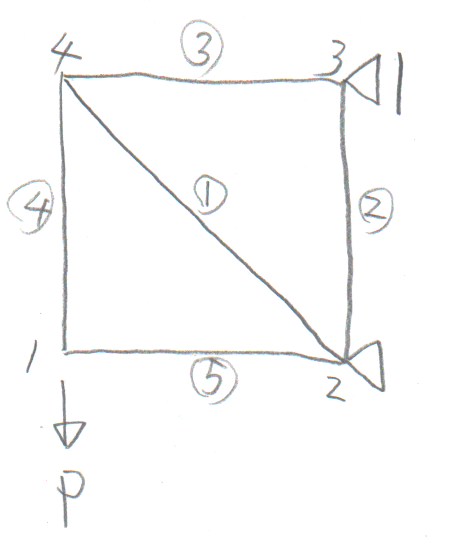 学籍番号の末尾が2か8の人。
学籍番号の末尾が2か8の人。
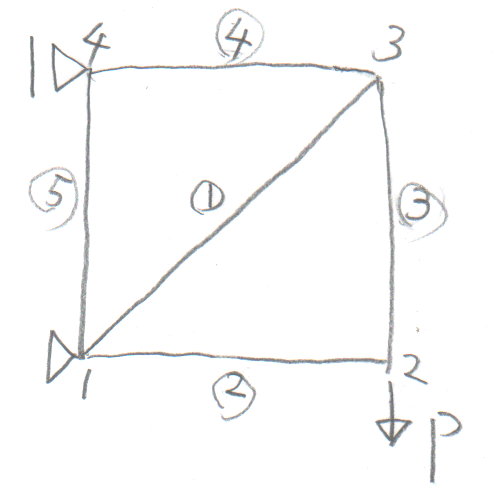 学籍番号の末尾が3か9の人。
学籍番号の末尾が3か9の人。
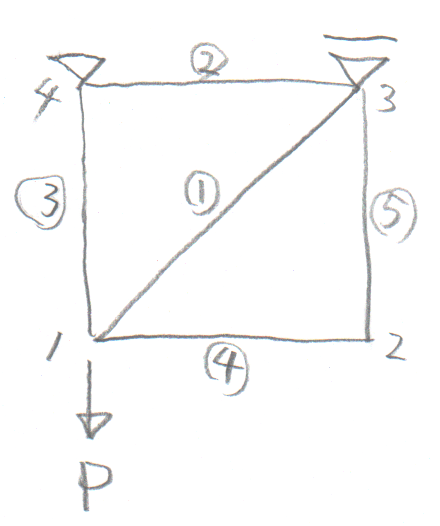 学籍番号の末尾が4か6の人。
学籍番号の末尾が4か6の人。
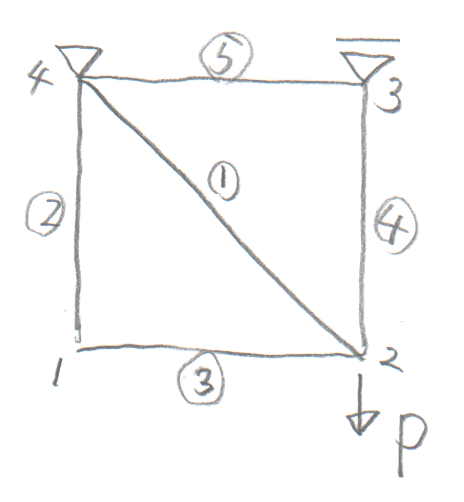 学籍番号の末尾が5か0の人。
学籍番号の末尾が5か0の人。
import math
# 1始まり配列を作るユーティリティ
def zeros1d(n):
return [0.0] * (n + 1) # 0番目はダミー
def zeros2d(n, m):
return [[0.0] * (m + 1) for _ in range(n + 1)]
def zeros3d(n, m, l):
return [[[0.0] * (l + 1) for _ in range(m + 1)] for _ in range(n + 1)]
# ---- サブルーチン ----
def zahyou(t, theta):
for i in range(1, 4):
for j in range(1, 4):
t[i+3][j] = 0.0
t[i][j+3] = 0.0
t[1][1] = math.cos(theta)
t[1][2] = math.sin(theta)
t[2][1] = -math.sin(theta)
t[2][2] = math.cos(theta)
t[3][3] = 1.0
t[4][4] = t[1][1]
t[4][5] = t[1][2]
t[5][4] = t[2][1]
t[5][5] = t[2][2]
t[6][6] = 1.0
def mxmx(a, b, c):
for i in range(1, 7):
for j in range(1, 7):
c[i][j] = 0.0
for k in range(1, 7):
c[i][j] += a[i][k] * b[k][j]
def mxtmx(a, b, c):
for i in range(1, 7):
for j in range(1, 7):
c[i][j] = 0.0
for k in range(1, 7):
c[i][j] += a[k][i] * b[k][j]
def gausu(n, a, x, b):
# 前進消去
for k in range(1, n):
for i in range(k+1, n+1):
for j in range(k+1, n+1):
a[i][j] -= a[k][j] * a[i][k] / a[k][k]
b[i] -= b[k] * a[i][k] / a[k][k]
# 後退代入
x[n] = b[n] / a[n][n]
for k in range(n, 0, -1):
akjxj = 0.0
for j in range(k+1, n+1):
akjxj += a[k][j] * x[j]
x[k] = (b[k] - akjxj) / a[k][k]
# ---- メインプログラム ----
# 配列定義
f = zeros1d(27) #節点力ベクトル
d = zeros1d(27) #節点変位ベクトル
x = zeros1d(27) #境界条件(拘束節点に0, その他に1が入る)
ss = zeros2d(27, 27) #全体剛性行列
xv = zeros1d(9) #節点ごとの変位境界 y方向
xw = zeros1d(9) #節点ごとの変位境界 z方向
xt = zeros1d(9) #節点ごとの変位境界 回転
fy = zeros1d(9) #節点ごとの荷重条件 z方向
fz = zeros1d(9) #節点ごとの荷重条件 y方向
cx = zeros1d(9) #節点ごとの荷重条件 モーメント外力
hidari = zeros1d(9) #各要素の左節点番号
migi = zeros1d(9) #各要素の右節点番号
s = zeros3d(9, 6, 6) #要素剛性行列
th = zeros1d(9) #各要素の回転角
t = zeros2d(6, 6) #座標変換行列(1要素ごとに計算)
s66 = zeros2d(6, 6) #要素剛性行列(1要素ごとに移し替える入れ物)
ts = zeros2d(6, 6) #TK(1要素ごとに計算)
tst = zeros2d(6, 6) #TKT(1要素ごとに計算)
snm = zeros1d(6) #節点力の出力のために追加
pi = math.asin(1.0) * 2.0
nyou = 5 #要素数
nset = 4 #節点数
# 初期化
for n in range(1, nyou+1):
for i in range(1, 7):
for j in range(1, 7):
s[n][i][j] = 0.0
for i in range(1, 28):
d[i] = 0.0
for j in range(1, 28):
ss[i][j] = 0.0
for i in range(1, 10):
xv[i] = 1.0
xw[i] = 1.0
xt[i] = 1.0
fy[i] = 0.0
fz[i] = 0.0
cx[i] = 0.0
# 要素1の剛性マトリクス
el = 1000.0 #1要素の長さ[mm]
ea = 10.0e3 * 10.0**2 #EA, ヤング率[N/mm^2]*面積[mm^2]
ei = 10.0e3 * 10.0**4 / 12.0 #EI, ヤング率[N/mm^2]*断面2次モーメント[mm^4]
s[1][2][2] = ea/el
s[1][2][5] = -ea/el
s[1][5][2] = -ea/el
s[1][5][5] = ea/el
s[1][1][1] = 12.0*ei/el**3
s[1][1][3] = -6.0*ei/el**2
s[1][1][4] = -12.0*ei/el**3
s[1][1][6] = -6.0*ei/el**2
s[1][3][1] = -6.0*ei/el**2
s[1][3][3] = 4.0*ei/el
s[1][3][4] = 6.0*ei/el**2
s[1][3][6] = 2.0*ei/el
s[1][4][1] = -12.0*ei/el**3
s[1][4][3] = 6.0*ei/el**2
s[1][4][4] = 12.0*ei/el**3
s[1][4][6] = 6.0*ei/el**2
s[1][6][1] = -6.0*ei/el**2
s[1][6][3] = 2.0*ei/el
s[1][6][4] = 6.0*ei/el**2
s[1][6][6] = 4.0*ei/el
#要素2から要素4までの剛性マトリクス
for k in range(2, 5):
for i in range(1, 7):
for j in range(1, 7):
s[k][i][j] = s[1][i][j]
#要素5の剛性マトリクス
el = el * math.sqrt(2.0)
s[5][2][2] = ea/el
s[5][2][5] = -ea/el
s[5][5][2] = -ea/el
s[5][5][5] = ea/el
s[5][1][1] = 12.0*ei/el**3
s[5][1][3] = -6.0*ei/el**2
s[5][1][4] = -12.0*ei/el**3
s[5][1][6] = -6.0*ei/el**2
s[5][3][1] = -6.0*ei/el**2
s[5][3][3] = 4.0*ei/el
s[5][3][4] = 6.0*ei/el**2
s[5][3][6] = 2.0*ei/el
s[5][4][1] = -12.0*ei/el**3
s[5][4][3] = 6.0*ei/el**2
s[5][4][4] = 12.0*ei/el**3
s[5][4][6] = 6.0*ei/el**2
s[5][6][1] = -6.0*ei/el**2
s[5][6][3] = 2.0*ei/el
s[5][6][4] = 6.0*ei/el**2
s[5][6][6] = 4.0*ei/el
#各要素の左節点番号、右節点番号
hidari[1]=1; migi[1]=2
hidari[2]=2; migi[2]=3
hidari[3]=3; migi[3]=4
hidari[4]=4; migi[4]=1
hidari[5]=1; migi[5]=3
#各要素の回転角(上の左右節点番号がz軸に横たわる状態からの)
th[1]=0.0
th[2]=pi/2.0
th[3]=pi
th[4]=pi+pi/2.0
th[5]=pi/4.0
# 境界条件
xv[1]=0.0
xw[1]=0.0
xv[2]=0.0
for i in range(1, 10):
x[3*i-2] = xv[i]
x[3*i-1] = xw[i]
x[3*i] = xt[i]
# 荷重条件(y方向:fy[節点番号], z方向:fz[節点番号], モーメント外力:cx[節点番号])
fz[3]=500.0 #[N]
for i in range(1, 10):
f[3*i-2] = fy[i]
f[3*i-1] = fz[i]
f[3*i] = cx[i]
# 要素ごとのTKTの計算
for n in range(1, nyou+1):
zahyou(t, th[n])
for i in range(1, 7):
for j in range(1, 7):
s66[i][j] = s[n][i][j]
mxtmx(t, s66, ts)
mxmx(ts, t, tst)
i1 = 3*hidari[n]-2
i2 = 3*hidari[n]-1
i3 = 3*hidari[n]
m1 = 3*migi[n]-2
m2 = 3*migi[n]-1
m3 = 3*migi[n]
ss[i1][i1] += tst[1][1]
ss[i1][i2] += tst[1][2]
ss[i1][i3] += tst[1][3]
ss[i1][m1] += tst[1][4]
ss[i1][m2] += tst[1][5]
ss[i1][m3] += tst[1][6]
ss[i2][i1] += tst[2][1]
ss[i2][i2] += tst[2][2]
ss[i2][i3] += tst[2][3]
ss[i2][m1] += tst[2][4]
ss[i2][m2] += tst[2][5]
ss[i2][m3] += tst[2][6]
ss[i3][i1] += tst[3][1]
ss[i3][i2] += tst[3][2]
ss[i3][i3] += tst[3][3]
ss[i3][m1] += tst[3][4]
ss[i3][m2] += tst[3][5]
ss[i3][m3] += tst[3][6]
ss[m1][i1] += tst[4][1]
ss[m1][i2] += tst[4][2]
ss[m1][i3] += tst[4][3]
ss[m1][m1] += tst[4][4]
ss[m1][m2] += tst[4][5]
ss[m1][m3] += tst[4][6]
ss[m2][i1] += tst[5][1]
ss[m2][i2] += tst[5][2]
ss[m2][i3] += tst[5][3]
ss[m2][m1] += tst[5][4]
ss[m2][m2] += tst[5][5]
ss[m2][m3] += tst[5][6]
ss[m3][i1] += tst[6][1]
ss[m3][i2] += tst[6][2]
ss[m3][i3] += tst[6][3]
ss[m3][m1] += tst[6][4]
ss[m3][m2] += tst[6][5]
ss[m3][m3] += tst[6][6]
# 境界条件を入れる
for i in range(1, nset*3+1):
for j in range(1, nset*3+1):
ss[i][j] = x[i] * ss[i][j]
ss[j][i] = x[i] * ss[j][i]
for i in range(1, nset*3+1):
if x[i] < 1e-3:
ss[i][i] = 1.0
# 線形方程式を解く
gausu(nset*3, ss, d, f)
# 結果出力
for n in range(1, nset+1):
print(f"節点番号:{n} v={d[n*3-2]}, w={d[n*3-1]}, th={d[n*3]}")
print(" 曲げモーメントの単位に注意!")
for n in range(1, nyou+1):
zahyou(t, th[n])
for i in range(1, 7):
for j in range(1, 7):
s66[i][j] = s[n][i][j]
mxtmx(t, s66, ts)
mxmx(ts, t, tst)
for i in range(1, 7):
snm[i] = 0.0
for j in range(1, 4):
snm[i] += tst[i][j] * d[(hidari[n]-1)*3 + j]
for j in range(4, 7):
snm[i] += tst[i][j] * d[(migi[n]-1)*3 + j-3]
print(f"部材番号: {n} S({hidari[n]})={snm[1]:15.10f}, N({hidari[n]})={snm[2]:15.10f}, M({hidari[n]})={snm[3]:15.10f}")
print(f" S({migi[n]})={snm[4]:15.10f}, N({migi[n]})={snm[5]:15.10f}, M({migi[n]})={snm[6]:15.10f}")