
構造力学(基礎)目次
(授業動画)
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
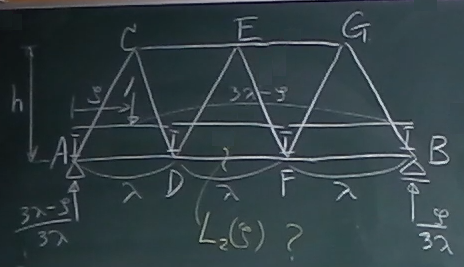 前回、間接荷重の影響線をやったが、今回は、
実構造物としての間接荷重の典型とも言える、トラスの部材力の影響線を
求めてみよう。
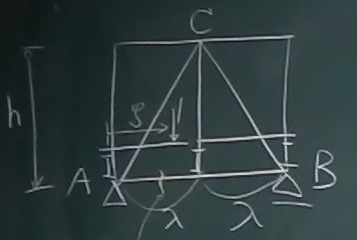
図のような、底辺$\lambda$, 高さ$h$の二等辺三角形が5個並んでいるワーレントラス
を考える。
$\lambda$はギリシャ文字の「ラムダ」。
書く時は、とりあえず漢字の「入」みたいに書いておけばいいだろう。
このトラスは下路トラスで、
下弦材の格点間を間接荷重区間とする間接載荷になっているものとする。
この図では、下弦材の格点部分に $\text{I}$ 型の横桁が載っていて、
横桁と横桁の間に縦桁が渡してあるが、
これはあくまで間接載荷のモデルである。
実際のトラス橋で、縦桁や横桁がどんな形状や配置になっていて、
それらを介して荷重が格点にどのように伝達されるか
というイメージは、
トラス橋 縦桁 横桁 格点とかで画像検索してみてほしい。
前回、間接荷重の影響線をやったが、今回は、
実構造物としての間接荷重の典型とも言える、トラスの部材力の影響線を
求めてみよう。
図のような、底辺$\lambda$, 高さ$h$の二等辺三角形が5個並んでいるワーレントラス
を考える。
$\lambda$はギリシャ文字の「ラムダ」。
書く時は、とりあえず漢字の「入」みたいに書いておけばいいだろう。
このトラスは下路トラスで、
下弦材の格点間を間接荷重区間とする間接載荷になっているものとする。
この図では、下弦材の格点部分に $\text{I}$ 型の横桁が載っていて、
横桁と横桁の間に縦桁が渡してあるが、
これはあくまで間接載荷のモデルである。
実際のトラス橋で、縦桁や横桁がどんな形状や配置になっていて、
それらを介して荷重が格点にどのように伝達されるか
というイメージは、
トラス橋 縦桁 横桁 格点とかで画像検索してみてほしい。
さて、今回は、下弦材DFの部材力の影響線を求めてみたい。
第4回の流儀で書くなら、
下弦材DFの部材力は、$N_{DF}$と書くべきだが、
過去の授業動画の資料と合わせるため、ここでは、$L_{2}$と書くことにする。
実際のトラスというのは、部材がいっぱいあるので、
下弦材(lower chord member)の部材力は、左から$L_{1}, L_{2}, L_{3}...$,
上弦材(upper chord member)の部材力は、左から$U_{1}, U_{2}, U_{3}...$,
斜材(diagonal member)の部材力は、左から$D_{1}, D_{2}, D_{3}...$,
みたいに書くことも多い。
まあ本質ではないので、書き方はどうでもいい。
部材力というのは、下弦材DFのどこで切っても同じ値だから、
この場合、どこか1つの点に着目しているわけではなくて、
下弦材DFに着目していることになる。つまり、
着目部材がDFということだ。
それだと考えにくいという場合は、
便宜的に
影響線の着目点は、下弦材DFのどこか適当なところ(例えば中点)と考えても
いい。どちらにしても、
単位荷重の位置$\zeta$によって、
下弦材DFの部材力$L_{2}$がどう変化するかを$\zeta$の関数として表したものが
影響線関数$L_{2}(\zeta)$となる。
まずは、反力を求める。 第4回でやったように 力のつりあいから求めればいいが、 このつりあいは、長さ$3\lambda$の単純梁を $\zeta : (3\lambda-\zeta)$に分ける点に単位荷重が作用している問題と 同じだから、 反力の公式を 使えば、 左端の反力が$\frac{3\lambda-\zeta}{3\lambda}$, 右端の反力が$\frac{\zeta}{3\lambda}$となる。
前回の梁の間接載荷と同じ様な考え方で、
1)荷重が着目部材のある間接荷重区間よりも左側の間接荷重区間にある場合
2)荷重が着目部材のある間接荷重区間にある場合
3)荷重が着目部材のある間接荷重区間よりも右側の間接荷重区間にある場合
の3つの場合に場合分けする。
今回の場合だと、以下のようになる。
1) $0\le \zeta\le\lambda$
2) $\lambda\le \zeta\le 2\lambda$
3) $2\lambda\le \zeta\le3\lambda$
着目部材が左から一番目の間接荷重区間にある場合は、上記の1)の場合はなくなるし、
着目部材が一番右側の間接荷重区間にある場合は、上記の3)の場合はなくなる。
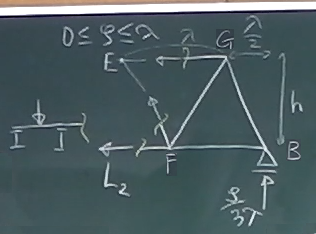 荷重が左から一番目の間接荷重区間($0\le z \le \lambda$)
にある場合、つまり$\zeta$が$0\le \zeta \le \lambda$となっているときの
着目部材DFでの部材力の影響線関数$L_{2}(\zeta)$を求める。
第4回の切断法でやったように、
着目部材を含めてトラス部材を3箇所で切ってトラスを2つのパーツに切り離し、
左側か右側のパーツを取り出してつりあいを考える。
このとき、間接荷重の横桁や縦桁は、取り除いて切り離し、
取り出したパーツに後から載せ直す
(単位荷重の位置によって、横桁への荷重の分配がない場合は、載せなくてよい)。
部材を図のような3箇所(元の図でいうなら、部材EG, EF, DFの3箇所)で
切り離した場合、左側のピースは、間接荷重が載っているから、
間接荷重を含まない右側のピースを取り出すことにする。
今、荷重の位置は、$0\le z \le \lambda$だから、
少なくとも格点Fの横桁には荷重は分配されない。
格点Eから右端Bまでの水平距離は、
三角形の底辺が1つと半分だから$\frac{3}{2}\lambda$である。
点E回りのモーメントのつりあいから、
荷重が左から一番目の間接荷重区間($0\le z \le \lambda$)
にある場合、つまり$\zeta$が$0\le \zeta \le \lambda$となっているときの
着目部材DFでの部材力の影響線関数$L_{2}(\zeta)$を求める。
第4回の切断法でやったように、
着目部材を含めてトラス部材を3箇所で切ってトラスを2つのパーツに切り離し、
左側か右側のパーツを取り出してつりあいを考える。
このとき、間接荷重の横桁や縦桁は、取り除いて切り離し、
取り出したパーツに後から載せ直す
(単位荷重の位置によって、横桁への荷重の分配がない場合は、載せなくてよい)。
部材を図のような3箇所(元の図でいうなら、部材EG, EF, DFの3箇所)で
切り離した場合、左側のピースは、間接荷重が載っているから、
間接荷重を含まない右側のピースを取り出すことにする。
今、荷重の位置は、$0\le z \le \lambda$だから、
少なくとも格点Fの横桁には荷重は分配されない。
格点Eから右端Bまでの水平距離は、
三角形の底辺が1つと半分だから$\frac{3}{2}\lambda$である。
点E回りのモーメントのつりあいから、
$\sum_{E}\circlearrowleft=-L_{2}h+\frac{\zeta}{3\lambda}\cdot\frac{3}{2}\lambda
=0$ よって、
$L_{2}(\zeta)=\frac{\zeta}{2h}\;\;\;\;(0\le\zeta\le\lambda)$
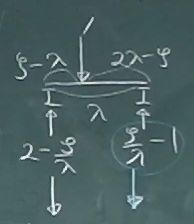 次に、左から2つ目の間接荷重区間
($\lambda\le z\le2\lambda$)
に荷重がある場合、つまり、
$\lambda\le \zeta\le2\lambda$ の場合を考える。
この場合、荷重のある間接荷重区間内に着目部材DFがあるから、
上と同様の3箇所でトラスを2つのピースに切り離したときに、
左側のピースの格点Dの横桁にも、
右側のピースの格点Fの横桁にも、
荷重が分配されてしまう。
どちらのピースを取り出しても荷重の分配を考えざるを得ないので、
梁の間接荷重のときと同じ要領で、
格点の上に載っている縦桁から考えていく。
縦桁部分は、単純梁として、下のトラス下弦材から切り離して考えればよい。
縦桁
($\lambda\le z\le2\lambda$)
の左端($z=\lambda$)から
単位荷重の載荷位置($z=\zeta$)までの
長さは$\zeta-\lambda$だし、
単位荷重の載荷位置($z=\zeta$)から
縦桁の右端($z=2\lambda$)までの
長さは$2\lambda-\zeta$だから、
この縦桁の両端の反力は、
反力の公式から、
次に、左から2つ目の間接荷重区間
($\lambda\le z\le2\lambda$)
に荷重がある場合、つまり、
$\lambda\le \zeta\le2\lambda$ の場合を考える。
この場合、荷重のある間接荷重区間内に着目部材DFがあるから、
上と同様の3箇所でトラスを2つのピースに切り離したときに、
左側のピースの格点Dの横桁にも、
右側のピースの格点Fの横桁にも、
荷重が分配されてしまう。
どちらのピースを取り出しても荷重の分配を考えざるを得ないので、
梁の間接荷重のときと同じ要領で、
格点の上に載っている縦桁から考えていく。
縦桁部分は、単純梁として、下のトラス下弦材から切り離して考えればよい。
縦桁
($\lambda\le z\le2\lambda$)
の左端($z=\lambda$)から
単位荷重の載荷位置($z=\zeta$)までの
長さは$\zeta-\lambda$だし、
単位荷重の載荷位置($z=\zeta$)から
縦桁の右端($z=2\lambda$)までの
長さは$2\lambda-\zeta$だから、
この縦桁の両端の反力は、
反力の公式から、
左端では$\frac{2\lambda-\zeta}{\lambda}\cdot 1=2-\frac{\zeta}{\lambda}$
右端では$\frac{\zeta-\lambda}{\lambda}\cdot 1=\frac{\zeta}{\lambda}-1$
これらの反力が作用・反作用の関係で、下のトラスの横桁の位置に載荷されている
と考えて、下のトラスを解けばよい。
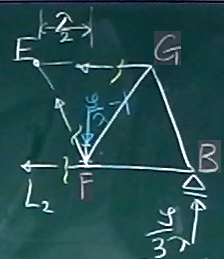 とういことで、これらの反力が格点DとFに載荷された状態のトラスを、
さきほどと同様の3箇所で切断し、
今回も右側のピースを取り出す。
格点Fには、縦桁の右端の反力$\frac{\zeta}{\lambda}-1$が作用・反作用で載荷されている。
点Eから点Fまでの水平距離は、$\frac{\lambda}{2}$, 点Eから点Bまでの水平距離は
$\frac{3}{2}\lambda$である。
点E回りのモーメントのつりあいから、
とういことで、これらの反力が格点DとFに載荷された状態のトラスを、
さきほどと同様の3箇所で切断し、
今回も右側のピースを取り出す。
格点Fには、縦桁の右端の反力$\frac{\zeta}{\lambda}-1$が作用・反作用で載荷されている。
点Eから点Fまでの水平距離は、$\frac{\lambda}{2}$, 点Eから点Bまでの水平距離は
$\frac{3}{2}\lambda$である。
点E回りのモーメントのつりあいから、
$\sum_{E}\circlearrowleft=-L_{2}h-(\frac{\zeta}{\lambda}-1)\cdot\frac{\lambda}{2}
+\frac{\zeta}{3\lambda}\cdot\frac{3}{2}\lambda
=0$ よって、
$L_{2}(\zeta)=\frac{\lambda}{2h}\;\;\;\;(\lambda\le\zeta\le 2\lambda)$
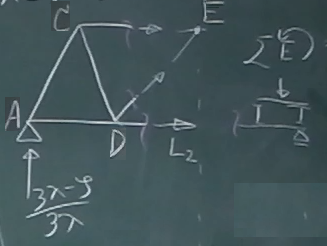 荷重が一番右端の間接荷重区間($2\lambda\le z \le 3\lambda$)
にある場合、つまり$\zeta$が$2\lambda\le \zeta \le 3\lambda$となっているときの
着目部材DFでの部材力の影響線関数$L_{2}(\zeta)$を求める。
トラスの切断方法は、今までと同じ3箇所で2つのピースに切り離す。
今回は、荷重が$2\lambda\le \zeta \le 3\lambda$にあるので、
間接荷重は格点FとBに分配されている。右側のピースは格点FもBも含むので、
今回は
荷重が分配されない左側のピースを取り出してつりあいを考える。
点Aから点Eまでの水平距離は$\frac{3}{2}\lambda$である。
点E回りのモーメントのつりあいから、
荷重が一番右端の間接荷重区間($2\lambda\le z \le 3\lambda$)
にある場合、つまり$\zeta$が$2\lambda\le \zeta \le 3\lambda$となっているときの
着目部材DFでの部材力の影響線関数$L_{2}(\zeta)$を求める。
トラスの切断方法は、今までと同じ3箇所で2つのピースに切り離す。
今回は、荷重が$2\lambda\le \zeta \le 3\lambda$にあるので、
間接荷重は格点FとBに分配されている。右側のピースは格点FもBも含むので、
今回は
荷重が分配されない左側のピースを取り出してつりあいを考える。
点Aから点Eまでの水平距離は$\frac{3}{2}\lambda$である。
点E回りのモーメントのつりあいから、
$\sum_{E}\circlearrowleft=-\frac{3\lambda-\zeta}{3\lambda}\cdot\frac{3}{2}\lambda
+L_{2}h=0$ よって、
$L_{2}(\zeta)=\frac{3\lambda-\zeta}{2h}\;\;\;\;(2\lambda\le\zeta\le 3\lambda)$
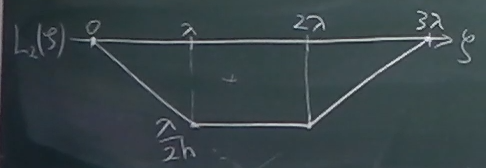
求めた影響線関数を間接荷重区間ごとに整理して、
それぞれの区間の両端の値を求める。
$
L_{2}(\zeta)=
\begin{cases}
\frac{\zeta}{2h}&\;\;\;\;(0\le\zeta\le\lambda)
\;\;\;\;L_{2}(0)=0, \; L_{2}(\lambda)=\frac{\lambda}{2h}
\\
\frac{\lambda}{2h}&\;\;\;\;(\lambda\le\zeta\le 2\lambda)\\
\frac{3\lambda-\zeta}{2h}&\;\;\;\;(2\lambda\le\zeta\le 3\lambda)
\;\;\;\;L_{2}(2\lambda)=\frac{\lambda}{2h}, \;L_{2}(3\lambda)=0
\\
\end{cases}
$
 部材力の影響線は、下を正にしておく。次項で述べるように
梁の曲げモーメントの影響線からも求められるので、
曲げモーメントの影響線の向きとひとまず合わせておく。
影響線関数は、どの区間でも$\zeta$の1次式または定数で直線だから、
各区間の両端の値を直線で結べばよい。
すると、図のようになる。
部材力の影響線は、下を正にしておく。次項で述べるように
梁の曲げモーメントの影響線からも求められるので、
曲げモーメントの影響線の向きとひとまず合わせておく。
影響線関数は、どの区間でも$\zeta$の1次式または定数で直線だから、
各区間の両端の値を直線で結べばよい。
すると、図のようになる。
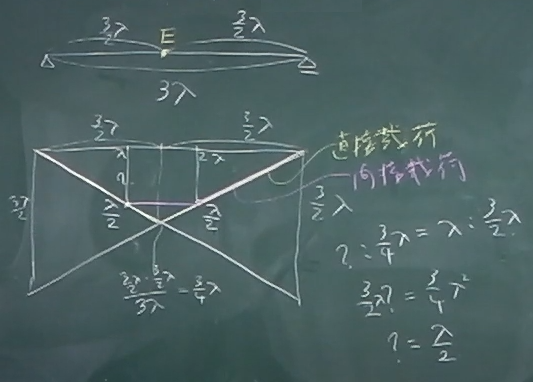 トラスの影響線は、前回やった
間接載荷の梁のモーメントの影響線を利用して描くこともできる。
例えば、トラスの全長が$3\lambda$だから、長さ$3\lambda$の単純梁を考える。
着目点は、
トラスの着目部材DFの例えば真ん中と考えて、
梁の真ん中に着目点Eを取る。
影響線の公式で点Eの
曲げモーメントの影響線を描き、
間接荷重区間$\lambda\le \zeta \le 2\lambda$の両端を直線で結ぶ。
そうすると、もう形としては、トラスの影響線が描けている。
縦軸は、モーメントの次元になっているが、これをトラスの高さ
$h$で割るとトラスの部材力の影響線となる。
トラスの影響線は、前回やった
間接載荷の梁のモーメントの影響線を利用して描くこともできる。
例えば、トラスの全長が$3\lambda$だから、長さ$3\lambda$の単純梁を考える。
着目点は、
トラスの着目部材DFの例えば真ん中と考えて、
梁の真ん中に着目点Eを取る。
影響線の公式で点Eの
曲げモーメントの影響線を描き、
間接荷重区間$\lambda\le \zeta \le 2\lambda$の両端を直線で結ぶ。
そうすると、もう形としては、トラスの影響線が描けている。
縦軸は、モーメントの次元になっているが、これをトラスの高さ
$h$で割るとトラスの部材力の影響線となる。
こういう方法は、部材がいっぱいあるトラスの設計等の実務では有用であるが、
プラットトラスやハウトラスといった形の違うトラスごとに、
着目点をどこに取るべきかということには注意が必要となる。
まあ、実務の際は、構造力学公式集に載っているトラスの影響線の公式を
利用すればいいのだとは思うし、
今は、公式集レベルの計算なんて、ソフトウェアに数値を入力するだけで
計算できたりするかもしれないが、
どんな構造でも(まあ、静定構造なら)、適切に部材を切断して、
適切に場合分けをして、
力のつりあいを考えれば解けるということは理解してほしい。
そうすれば、公式集に載ってない新たな静定トラス構造みたいなものが
提案されたとしても、どうやって解けばいいかがわかる
(複雑な構造ならプログラムを組んでもいいし)ということが重要なことかなと思う。
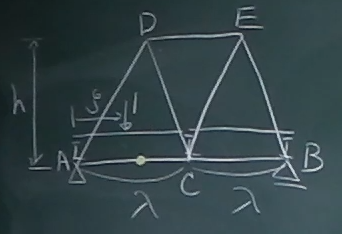 左から1番目の下弦材ACの部材力の影響線関数
$L_{AC}(\zeta)$を求め、
その影響線(下が正)を描け。
答えは、
ここ。
動画の解説は、
第15回 例題1。
左から1番目の下弦材ACの部材力の影響線関数
$L_{AC}(\zeta)$を求め、
その影響線(下が正)を描け。
答えは、
ここ。
動画の解説は、
第15回 例題1。
 左から1番目の下弦材
(左下の黄色の波線で切断線を入れてある部材)の部材力の影響線関数
$L_{1}(\zeta)$を求め、
その影響線(下が正)を描け。
答えは、
ここ。
動画の解説は、
第15回 例題2。
左から1番目の下弦材
(左下の黄色の波線で切断線を入れてある部材)の部材力の影響線関数
$L_{1}(\zeta)$を求め、
その影響線(下が正)を描け。
答えは、
ここ。
動画の解説は、
第15回 例題2。
2021年度小テスト:
問題,
解答
2020年度小テスト:
問1,
問2,
解答
メモ: