
マトリクス構造解析オンライン授業用テキスト
第13回オンライン授業
YouTube授業動画リスト
小さい字は補足説明なので、読み飛ばしてもいいです。
 前回、プログラム(torasu2.py)の
使い方をやったので、このプログラムを使って、今回は、
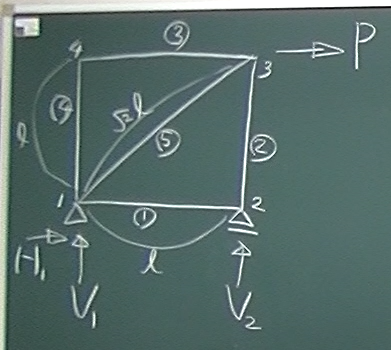
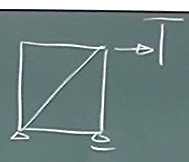
図のような、トラスを解いてみたい。
まず、正解を単位荷重法で求めておく。
伸び剛性は$EA$とするが、今回は、想像できるぐらいの大きさ、固さの
材料諸元で解いてみよう。
ホームセンターに売ってるような
10mm角の角材1m(斜材は$\sqrt{2}$m)で、図のようなトラスを作って、
50kgfぐらいの体重で引っ張ったぐらい
(図のトラスを90$^{\circ}$回転させて壁に固定して、人がぶら下がったぐらい)の
問題を想定して、
前回、プログラム(torasu2.py)の
使い方をやったので、このプログラムを使って、今回は、
図のような、トラスを解いてみたい。
まず、正解を単位荷重法で求めておく。
伸び剛性は$EA$とするが、今回は、想像できるぐらいの大きさ、固さの
材料諸元で解いてみよう。
ホームセンターに売ってるような
10mm角の角材1m(斜材は$\sqrt{2}$m)で、図のようなトラスを作って、
50kgfぐらいの体重で引っ張ったぐらい
(図のトラスを90$^{\circ}$回転させて壁に固定して、人がぶら下がったぐらい)の
問題を想定して、
$E=10$GPa$=10000$N/mm$^{2}$
$A=(10$mm$)^{2}=100$mm$^{2}$
$\ell=1$m$=1000$mm
$P=500$N
とする。
$\sum\uparrow=V_{1}+V_{2}=0$
$\sum\rightarrow=H_{1}+P=0\;$ よって、$H_{1}=-P$
$\sum_{1}\circlearrowleft=V_{2}\ell-P\ell=0\;$よって、$V_{2}=P$
よって、$V_{1}=-P$
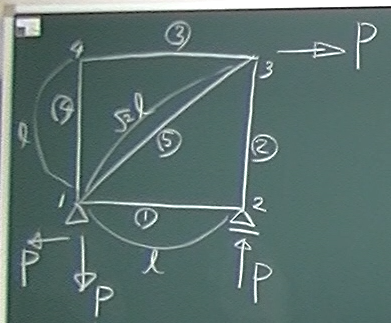 反力は求まったので、次に各要素の部材力を求める。
まず要素③、⑤、①を切断して、トラスを2つのピースに切り離し、
今回は左側のピースを取り出してつりあいを考える。
反力は求まったので、次に各要素の部材力を求める。
まず要素③、⑤、①を切断して、トラスを2つのピースに切り離し、
今回は左側のピースを取り出してつりあいを考える。
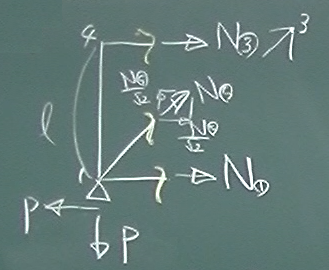 $\sum_{1}\circlearrowright=N_{③}\ell=0$よって、$N_{③}=0$
$\sum_{1}\circlearrowright=N_{③}\ell=0$よって、$N_{③}=0$
$\sum_{3}\circlearrowleft=N_{①}\ell-P\ell+P\ell=0$よって、$N_{①}=0$
$\sum\uparrow=\frac{N_{⑤}}{\sqrt{2}}-P=0\;$ よって、$N_{⑤}=\sqrt{2}P$
 次に、要素④と③を切断して、節点4側のピースを取り出す。
$N_{③}=0$と上で求まっているから、
$N_{④}$しか力はないので、力のつりあいから、$N_{④}=0$
次に、要素④と③を切断して、節点4側のピースを取り出す。
$N_{③}=0$と上で求まっているから、
$N_{④}$しか力はないので、力のつりあいから、$N_{④}=0$
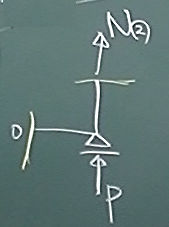 次に、要素①と②を切断して、節点2側のピースを取り出す。
$N_{①}=0$と上で求まっているから、
力のつりあいから、
次に、要素①と②を切断して、節点2側のピースを取り出す。
$N_{①}=0$と上で求まっているから、
力のつりあいから、
$\sum\uparrow=P+N_{②}=0\;$よって、
$N_{②}=-P$
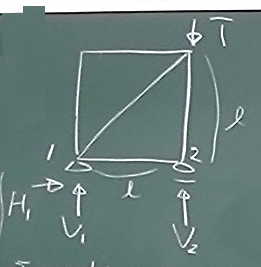
 まず、載荷点の$z$方向変位$w_{3}$を求めよう。
単位荷重法で求めるには、節点変位を求めたい節点の求めたい変位の方向に、
仮想単位荷重を載荷して、各節点力を求める。
元の構造の部材力の$P$に$1$を代入すればいいから、この仮想構造の部材力は、
以下のように求まる。
まず、載荷点の$z$方向変位$w_{3}$を求めよう。
単位荷重法で求めるには、節点変位を求めたい節点の求めたい変位の方向に、
仮想単位荷重を載荷して、各節点力を求める。
元の構造の部材力の$P$に$1$を代入すればいいから、この仮想構造の部材力は、
以下のように求まる。
$\overline{N}_{①}=\overline{N}_{③}=\overline{N}_{④}=0$
$\overline{N}_{②}=-1$
$\overline{N}_{⑤}=\sqrt{2}$
第5回でやったように
公式から、
$$\overline{1}\cdot w_{3}
=\int_{全部材}\frac{N\overline{N}}{EA}dz^{\ell}$$
$$=\frac{1}{EA}\left(N_{②}\overline{N}_{②}\ell+N_{⑤}\overline{N}_{⑤}\cdot \sqrt{2}\ell
\right)$$
$$=\frac{1}{EA}\left( (-P)(-1)\ell + \sqrt{2}P\cdot\sqrt{2}\cdot\sqrt{2}\ell \right)$$
$$=(1+2\sqrt{2})\frac{P\ell}{EA}\simeq 3.8284271\frac{P\ell}{EA}$$
$\frac{P\ell}{EA}$に、冒頭に示した以下の諸元を代入すると
$E=10$GPa$=10000$N/mm$^{2}$
$A=(10$mm$)^{2}=100$mm$^{2}$
$\ell=1$m$=1000$mm
$P=500$N
$$\frac{P\ell}{EA}=
\frac{500\text{N}\times 1000\text{mm}}{10000\text{N}/\text{mm}^{2}
\times 100\text{mm}^{2}}=0.5\text{mm}$$
すると
$w_{3}=(1+2\sqrt{2})\times 0.5
\simeq 1.914213562373\text{mm}$
つまり、だいたい 2mm ぐらいということだ。
 $v_{3}$を求めるには、
節点3の$v_{3}$方向に、単位荷重を与えて各要素の部材力を求める。
$v_{3}$を求めるには、
節点3の$v_{3}$方向に、単位荷重を与えて各要素の部材力を求める。
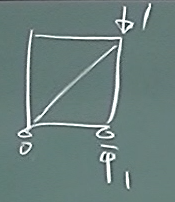 この場合、反力は、$V_{2}=1$だけだから、
この場合、反力は、$V_{2}=1$だけだから、
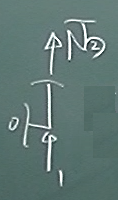 $\sum\uparrow=1+\overline{N}_{②}=0\;$
よって、
$\overline{N}_{②}=-1$
$\sum\uparrow=1+\overline{N}_{②}=0\;$
よって、
$\overline{N}_{②}=-1$
その他の要素の部材力はすべて0.
上で解いた
元の構造の要素②の部材力は、${N}_{②}=-P$
公式から、
$$\overline{1}\cdot v_{3}
=\int_{全部材}\frac{N\overline{N}}{EA}dz^{\ell}$$
$$=\frac{1}{EA}\left(N_{②}\overline{N}_{②}\ell\right)$$
$$=\frac{1}{EA}\left( (-P)(-1)\cdot \ell \right)$$
$$=\frac{P\ell}{EA}=0.5\text{mm}$$
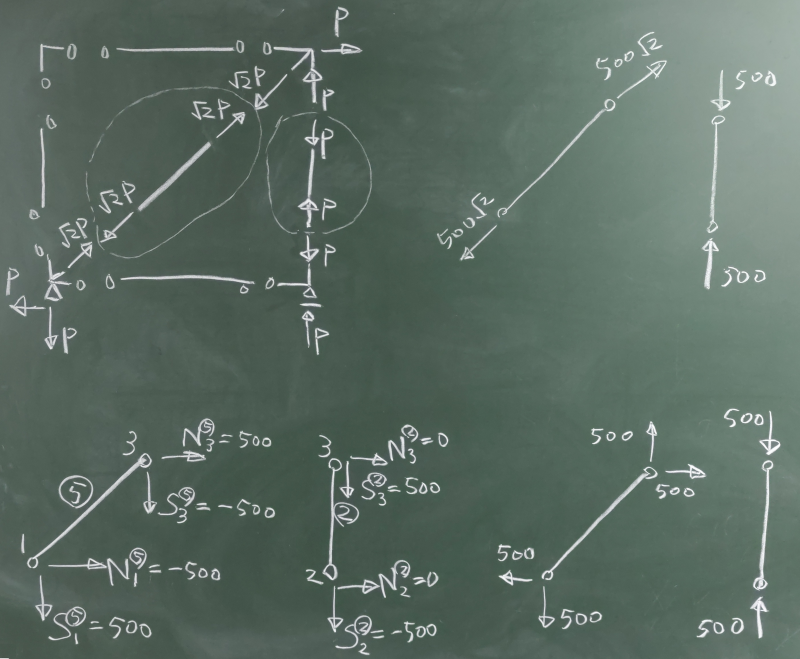 各要素を節点の近傍で切断して、部材力を書き込んでみると、
要素にゼロでない部材力が作用しているのは、⑤要素と②要素のみ。
⑤要素は$\sqrt{2}P=500\sqrt{2}$Nの引張、
②要素は$P=500$Nの圧縮。
ということは、これらを$yz$方向の節点力で表してやると、
各要素を節点の近傍で切断して、部材力を書き込んでみると、
要素にゼロでない部材力が作用しているのは、⑤要素と②要素のみ。
⑤要素は$\sqrt{2}P=500\sqrt{2}$Nの引張、
②要素は$P=500$Nの圧縮。
ということは、これらを$yz$方向の節点力で表してやると、
⑤要素の節点1に、$S_{1}^{⑤}=500$N, $N_{1}^{⑤}=-500$N
⑤要素の節点3に、$S_{3}^{⑤}=-500$N, $N_{3}^{⑤}=500$N
②要素の節点2に、$S_{2}^{②}=-500$N, $N_{2}^{②}=0$
②要素の節点3に、$S_{3}^{②}=500$N, $N_{3}^{②}=0$
では、 前回のプログラム(torasu2.py)を 使って、上のトラスを解いてみよう。 torasu2.pyを適当な別名(torasu5.pyとか)で保存し、 書き換えていく。
 今回は、要素数は5要素、節点数は4節点。
今回は、要素数は5要素、節点数は4節点。
nyou = 5 #要素数
nset = 4 #節点数
今回は、ホームセンターで売ってる10mm角の角材1mぐらいの材料で作った
トラスを体重ぐらいで引っ張るということで、
$E=10$GPa$=10000$N/mm$^{2}$
$A=(10$mm$)^{2}=100$mm$^{2}$
$\ell=1$m$=1000$mm
$P=500$N
を与える。
プログラムに与える単位系は、自分で決められるが、
今回は、小さいものを解くので、力はN, 長さはmmの単位系を使う。
そうすると、ヤング率($\frac{力}{{長さ}^{2}}$)は、N/mm$^{2}=$MPaで与えなければならない。
まず、要素①は長さ$\ell=1000$mmだから、
E = 10.0e3 #ヤング率 N/mm^2(MPa)
ell = 1000.0 #1要素の長さ mm
A = 10.0**2 #面積 mm^2
sk1 = E*A/ell #要素1のばね定数
# 要素剛性マトリクス
s[1][2][2] = sk1; s[1][2][4] = -sk1
s[1][4][2] = -sk1; s[1][4][4] = sk1
要素②、③、④はすべて長さ$\ell=1000$mmで要素①と同じだから、 要素①の剛性マトリクスs[1][i][j]をfor文を使って、 要素②、③、④の剛性マトリクスs[2][i][j], s[3][i][j], s[4][i][j]に そのまま代入すればよい。 あるいは、for文を書きたくなければ、上と同じように sk[2][2][2] = sk1; sk[2][2][4] = -sk1みたいに1要素ずつの剛性マトリクスを定義しても構わない。
#要素2から要素4までの剛性マトリクス
for k in range(2, 5):
for i in range(1, 5):
for j in range(1, 5):
s[k][i][j] = s[1][i][j]
s[k][i][j]のkは要素番号なので、k=2から4まで変化させながら、 それぞれのkに対して、①要素の剛性マトリクスs[1][i][j]を s[k][i][j]に代入する。 剛性マトリクスは$4\times 4$なのでiとjは、それぞれ1から4まで変化させる。 初期値は1からでも回数は0から数えるので5回で、range(1,5)となる。
要素⑤は長さ$\sqrt{2}\ell=1000\sqrt{2}$mmだから、 sk1$=k_{①}=\frac{EA}{\ell}$とすると、 sk5$=k_{⑤}=\frac{EA}{\sqrt{2}\ell}=k_{①}/\sqrt{2}=$sk1/sqrt(2) とすればよい。
#要素5の剛性マトリクス
sk5 = sk1 / math.sqrt(2.0) #要素5のばね定数
s[5][2][2] = sk5; s[5][2][4] = -sk5
s[5][4][2] = -sk5; s[5][4][4] = sk5
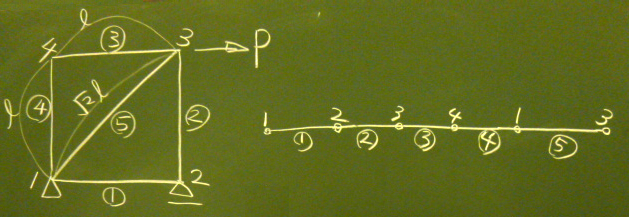 なるべく一筆書きできるように、
なるべく要素番号と節点番号が左から右に増えるように、
図のように、初期状態の要素を$z$軸上に並べる。
このトラスは、一筆書きで書けるので、1直線上に並ぶが、
複数の直線になっても構わない。
なるべく一筆書きできるように、
なるべく要素番号と節点番号が左から右に増えるように、
図のように、初期状態の要素を$z$軸上に並べる。
このトラスは、一筆書きで書けるので、1直線上に並ぶが、
複数の直線になっても構わない。
各要素ごとに、初期状態での左節点番号(idari)と右節点番号(migi)を与える。
#各要素の左節点番号、右節点番号
hidari[1] = 1; migi[1] = 2
hidari[2] = 2; migi[2] = 3
hidari[3] = 3; migi[3] = 4
hidari[4] = 4; migi[4] = 1
hidari[5] = 1; migi[5] = 3
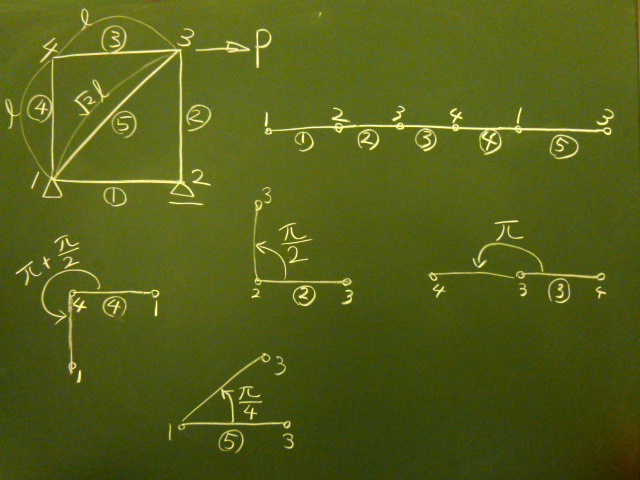 次に各要素の回転角を、初期状態での左節点を中心に反時計回りの回転角で与える。
$yz$平面の回転角は、$x$軸右ねじ回転なので、反時計回りになる。
次に各要素の回転角を、初期状態での左節点を中心に反時計回りの回転角で与える。
$yz$平面の回転角は、$x$軸右ねじ回転なので、反時計回りになる。
#各要素の回転角(上の左右節点番号がz軸に横たわる状態からの)
th[1] = 0.0
th[2] = pi/2.0
th[3] = pi
th[4] = pi+pi/2.0
th[5] = pi/4.0
次は境界条件である。 回転角の下の以下のように書いてあるところを見つける。
# 境界条件
xv[1] = 0.0; xw[1] = 0.0
xv[2] = 0.0
今回は、節点1で$v_{1}=w_{1}=0\;$, 節点2で、$v_{2}=0$
今回は、節点3の$z$方向に、500Nを与えるので、
# 荷重条件(y方向:fy[節点番号], z方向:fz[節点番号])
#fy[2] = 1.0
fz[3] = 500.0 #[N]
とする。ちなみに、$y$方向に与える場合は、fy[]を用いる。
プログラムの修正が終わったら、 修正したプログラムは、例えば"torasu5.py"みたいな名前で保存する。 プログラムを実行すると、以下のように表示される。
節点番号:1 v=0.0000000000, w=0.0000000000
節点番号:2 v=0.0000000000, w=-0.0000000000
節点番号:3 v=0.5000000000, w=1.9142135624
節点番号:4 v=0.0000000000, w=1.9142135624
部材番号: 1 S(1)= 0.0000000000, N(1)= 0.0000000000
S(2)= 0.0000000000, N(2)= -0.0000000000
部材番号: 2 S(2)=-500.0000000000, N(2)= 0.0000000000
S(3)= 500.0000000000, N(3)= -0.0000000000
部材番号: 3 S(3)= -0.0000000000, N(3)= -0.0000000000
S(4)= 0.0000000000, N(4)= 0.0000000000
部材番号: 4 S(4)= -0.0000000000, N(4)= 0.0000000000
S(1)= 0.0000000000, N(1)= 0.0000000000
部材番号: 5 S(1)= 500.0000000000, N(1)=-500.0000000000
S(3)=-500.0000000000, N(3)= 500.0000000000
単位荷重法では、$v_{3}=0.5$mm, $w_{3}=(1+2\sqrt{2})\times 0.5 \simeq 1.914213562373$mmと求まっていたが、 節点番号3のところを見ると、表示されている桁は四捨五入すると合っている。
 各要素を節点の近傍で切断して、部材力を書き込んでみると、
要素にゼロでない部材力が作用しているのは、⑤要素と②要素のみ。
⑤要素は$\sqrt{2}P=500\sqrt{2}$Nの引張、
②要素は$P=500$Nの圧縮。
ということは、これらを$yz$方向の節点力で表してやると、
各要素を節点の近傍で切断して、部材力を書き込んでみると、
要素にゼロでない部材力が作用しているのは、⑤要素と②要素のみ。
⑤要素は$\sqrt{2}P=500\sqrt{2}$Nの引張、
②要素は$P=500$Nの圧縮。
ということは、これらを$yz$方向の節点力で表してやると、
②要素の節点2に、$S_{2}^{②}=-500$N, $N_{2}^{②}=0$
②要素の節点3に、$S_{3}^{②}=500$N, $N_{3}^{②}=0$
⑤要素の節点1に、$S_{1}^{⑤}=500$N, $N_{1}^{⑤}=-500$N
⑤要素の節点3に、$S_{3}^{⑤}=-500$N, $N_{3}^{⑤}=500$N
以下の5要素トラス(自分の学籍番号のもの)の
載荷点の節点変位($v, w$)を単位荷重法で求めよ。
長さ$\ell$の水平、鉛直の4本の部材が正方形を作り、
長さ$\sqrt{2}\ell$の斜材が1本入っている。
$E=10$GPa$=10000$N/mm$^{2}$
$A=(10$mm$)^{2}=100$mm$^{2}$
$\ell=1$m$=1000$mm
$P=500$N
とする。
torasu5.pyで解いて、
手計算の答えとどれくらい合うか考察せよ。
WebClassの「プログラム課題5」から、
単位荷重法の手計算を撮影した画像と
プログラム本体(例えば torasu5_gotou.py とか)と、
出力ファイル(例えば kekka5.txt とか)を
それぞれアップロードせよ。
どうしてもエラーが取れないなどの場合は、
kekka5.txtの代わりに、エラー画面等
をテキストエディタに貼り付けて保存したものをアップロードする。
また、最後のコメント欄に、手計算とプログラムの計算とを比較した考察や、
うまく実行できなかった場合は、
どういう症状で実行できないのかの説明を書き込むこと。
要素番号は、初期状態で左から①②③④⑤の順番に並べれば、
一筆書きできるようにしているつもりだが、
一筆書きできないように並べたとしても、適切に節点番号を指定すれば、
解けるはずである。
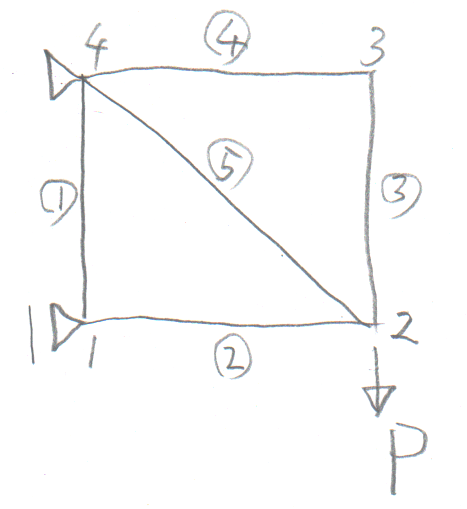 学籍番号の末尾が1か7の人。
学籍番号の末尾が1か7の人。
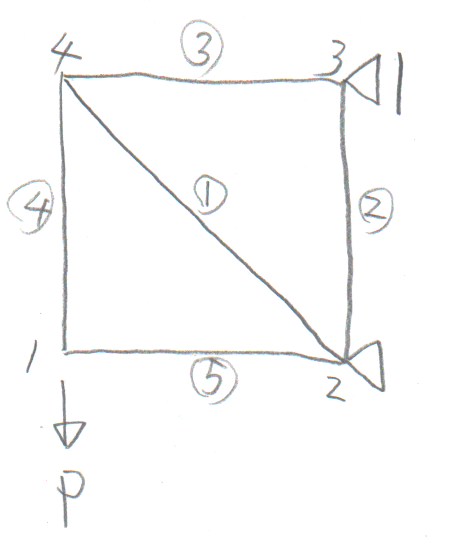 学籍番号の末尾が2か8の人。
学籍番号の末尾が2か8の人。
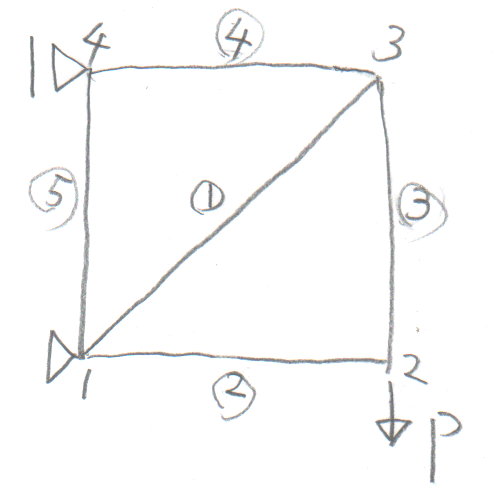 学籍番号の末尾が3か9の人。
学籍番号の末尾が3か9の人。
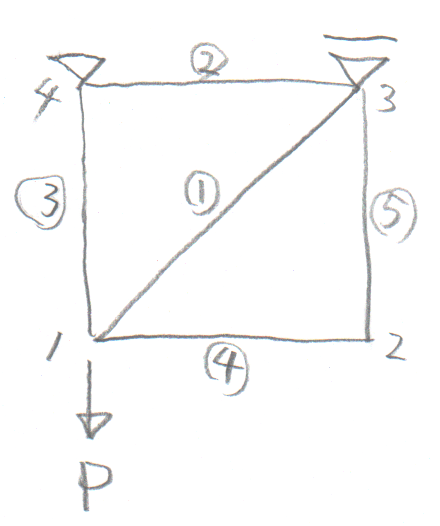 学籍番号の末尾が4か6の人。
学籍番号の末尾が4か6の人。
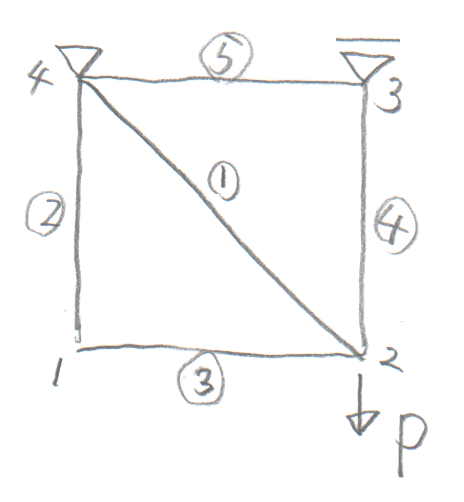 学籍番号の末尾が5か0の人。
学籍番号の末尾が5か0の人。
import math
def mxmx(a, b, c):
# c = a @ b
for i in range(1, 5):
for j in range(1, 5):
c[i][j] = 0.0
for k in range(1, 5):
c[i][j] += a[i][k] * b[k][j]
def zahyou(t, theta):
# 4x4座標変換行列
for i in range(1, 3):
for j in range(1, 3):
t[i+2][j] = 0.0
t[i][j+2] = 0.0
t[1][1] = math.cos(theta)
t[1][2] = math.sin(theta)
t[2][1] = -math.sin(theta)
t[2][2] = math.cos(theta)
t[3][3] = t[1][1]
t[3][4] = t[1][2]
t[4][3] = t[2][1]
t[4][4] = t[2][2]
def mxtmx(a, b, c):
# c = a^T @ b
for i in range(1, 5):
for j in range(1, 5):
c[i][j] = 0.0
for k in range(1, 5):
c[i][j] += a[k][i] * b[k][j]
def gausu(n, a, x, b):
# ガウス消去法による連立一次方程式 a x = b の解
# a: (n+1)x(n+1), x: (n+1), b: (n+1) (0番目ダミー)
for k in range(1, n):
for i in range(k+1, n+1):
for j in range(k+1, n+1):
a[i][j] -= a[k][j] * a[i][k] / a[k][k]
b[i] -= b[k] * a[i][k] / a[k][k]
# 後退代入
x[n] = b[n] / a[n][n]
for k in range(n-1, 0, -1):
akjxj = 0.0
for j in range(k+1, n+1):
akjxj += a[k][j] * x[j]
x[k] = (b[k] - akjxj) / a[k][k]
def main():
# 配列は0番目ダミー
f = [0.0] * 19 #節点力ベクトル
d = [0.0] * 19 #節点変位ベクトル
x = [0.0] * 19 #境界条件(拘束節点に0, その他に1が入る)
ss = [[0.0]*19 for _ in range(19)] #全体剛性行列
xv = [0.0] * 10 #節点ごとの変位境界 y方向
xw = [0.0] * 10 #節点ごとの変位境界 z方向
fy = [0.0] * 10 #節点ごとの荷重条件 y方向
fz = [0.0] * 10 #節点ごとの荷重条件 z方向
hidari = [0] * 10 #各要素の左節点番号
migi = [0] * 10 #各要素の右節点番号
s = [[[0.0]*5 for _ in range(5)] for _ in range(10)] #要素剛性行列
th = [0.0] * 10 #各要素の回転角
t = [[0.0]*5 for _ in range(5)] #座標変換行列(1要素ごとに計算)
s44 = [[0.0]*5 for _ in range(5)] #要素剛性行列(1要素ごとに移し替える入れ物)
ts = [[0.0]*5 for _ in range(5)] #TK(1要素ごとに計算)
tst = [[0.0]*5 for _ in range(5)] #TKT(1要素ごとに計算)
sn = [0.0] * 5 #節点力の出力のために追加
pi = math.pi
nyou = 5 #要素数
nset = 4 #節点数
# 初期化
for n in range(1, nyou+1):
for i in range(1, 5):
for j in range(1, 5):
s[n][i][j] = 0.0
for i in range(1, 19):
d[i] = 0.0
# f[i] = 0.0
# x[i] = 0.0
for j in range(1, 19):
ss[i][j] = 0.0
for i in range(1, 10):
xv[i] = 1.0
xw[i] = 1.0
fy[i] = 0.0
fz[i] = 0.0
E = 10.0e3 #ヤング率 N/mm^2(MPa)
ell = 1000.0 #1要素の長さ mm
A = 10.0**2 #面積 mm^2
sk1 = E*A/ell #要素1のばね定数
#要素剛性マトリクス
#要素1の剛性マトリクス
s[1][2][2] = sk1; s[1][2][4] = -sk1
s[1][4][2] = -sk1; s[1][4][4] = sk1
#要素2から要素4までの剛性マトリクス
for k in range(2, 5):
for i in range(1, 5):
for j in range(1, 5):
s[k][i][j] = s[1][i][j]
#要素5の剛性マトリクス
sk5 = sk1 / math.sqrt(2.0) #要素5のばね定数
s[5][2][2] = sk5; s[5][2][4] = -sk5
s[5][4][2] = -sk5; s[5][4][4] = sk5
#各要素の左節点番号、右節点番号
hidari[1] = 1; migi[1] = 2
hidari[2] = 2; migi[2] = 3
hidari[3] = 3; migi[3] = 4
hidari[4] = 4; migi[4] = 1
hidari[5] = 1; migi[5] = 3
#各要素の回転角(上の左右節点番号がz軸に横たわる状態からの)
th[1] = 0.0
th[2] = pi/2.0
th[3] = pi
th[4] = pi+pi/2.0
th[5] = pi/4.0
# 境界条件
xv[1] = 0.0; xw[1] = 0.0
xv[2] = 0.0
for i in range(1, 10):
x[2*i-1] = xv[i]
x[2*i] = xw[i]
# 荷重条件(y方向:fy[節点番号], z方向:fz[節点番号])
#fy[2] = 1.0
fz[3] = 500.0 #[N]
for i in range(1, 10):
f[2*i-1] = fy[i]
f[2*i] = fz[i]
# 要素ごとのTKTの計算
for n in range(1, nyou+1):
zahyou(t, th[n])
for i in range(1, 5):
for j in range(1, 5):
s44[i][j] = s[n][i][j]
mxtmx(t, s44, ts)
mxmx(ts, t, tst)
i1 = 2*hidari[n] - 1
i2 = 2*hidari[n]
m1 = 2*migi[n] - 1
m2 = 2*migi[n]
ss[i1][i1] += tst[1][1]
ss[i1][i2] += tst[1][2]
ss[i1][m1] += tst[1][3]
ss[i1][m2] += tst[1][4]
ss[i2][i1] += tst[2][1]
ss[i2][i2] += tst[2][2]
ss[i2][m1] += tst[2][3]
ss[i2][m2] += tst[2][4]
ss[m1][i1] += tst[3][1]
ss[m1][i2] += tst[3][2]
ss[m1][m1] += tst[3][3]
ss[m1][m2] += tst[3][4]
ss[m2][i1] += tst[4][1]
ss[m2][i2] += tst[4][2]
ss[m2][m1] += tst[4][3]
ss[m2][m2] += tst[4][4]
# 境界条件を入れる
for i in range(1, nset*2+1):
for j in range(1, nset*2+1):
ss[i][j] = x[i]*ss[i][j]
ss[j][i] = x[i]*ss[j][i]
for i in range(1, nset*2+1):
if x[i] < 1e-3:
ss[i][i] = 1.0
gausu(nset*2, ss, d, f)
for n in range(1, nset+1):
print(f"節点番号:{n} v={d[n*2-1]:.10f}, w={d[n*2]:.10f}")
# 要素ごとのTKTの計算
for n in range(1, nyou+1):
zahyou(t, th[n])
for i in range(1, 5):
for j in range(1, 5):
s44[i][j] = s[n][i][j]
mxtmx(t, s44, ts)
mxmx(ts, t, tst)
for i in range(1, 5):
sn[i] = 0.0
for j in range(1, 3):
sn[i] += tst[i][j] * d[(hidari[n]-1)*2 + j]
for j in range(3, 5):
sn[i] += tst[i][j] * d[(migi[n]-1)*2 + j-2]
print(f"部材番号: {n} S({hidari[n]})={sn[1]:15.10f}, N({hidari[n]})={sn[2]:15.10f}")
print(f" S({migi[n]})={sn[3]:15.10f}, N({migi[n]})={sn[4]:15.10f}")
if __name__ == "__main__":
main()