春休みの課題†
4/18†
- 鋼材の長方形断面の梁の片持ち梁と単純梁を曲げる
SS400のヤング率E : 205GPa, 降伏応力 : 235MPa
- 載荷点での荷重、たわみのプロット
- 片持ち梁の場合
固定していない方の面に荷重を掛けた(面載荷)ので、荷重を掛けた面上にあるどこか一つの点を選択して荷重ーたわみ曲線を作成する。
- ある点の座標を時間経過(1.0sの0.1s刻み = 10ステップ)ごとに表示させてそれをCSVファイルで保存したい
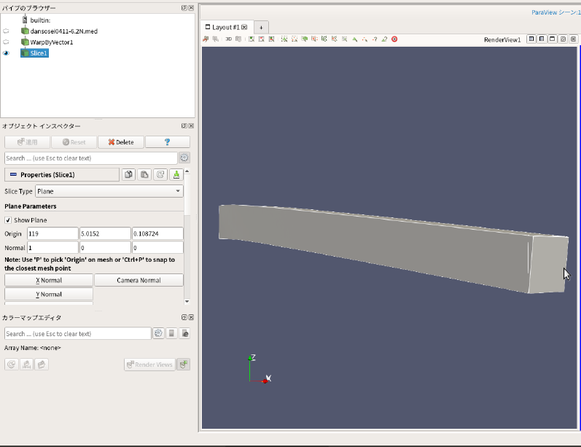
- Sliceを選択してオブジェクトインスペクター内にある Plane Parameters でSliceする位置を記入するとその面におけるたわみや応力の情報を確認できる(SpreadSheetViewで)。
- 梁モデルの変形が大きすぎるとSliceの位置をx=120に設定した際に断面が縦方向に潰れたり消失したりすることがあるが、Sliceする位置を118, 119とかにすると大体解決する(左上図)
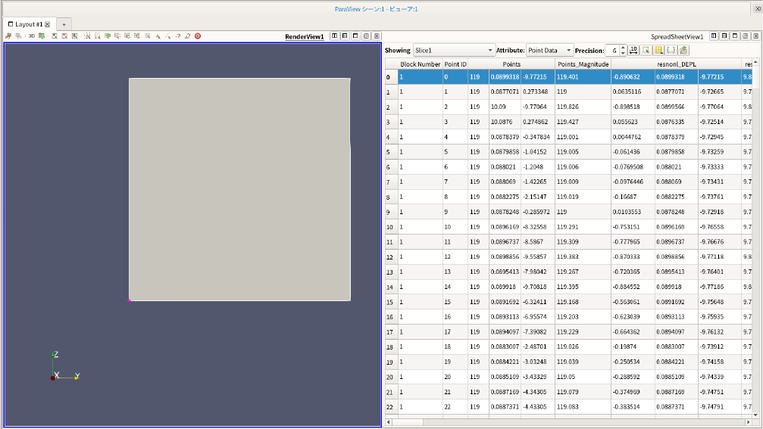
- 右上はSliceした面上にある1点を選択したときの写真で、右の表のどこかを選択状態にする(青くなる)と左側のモデルにピンクの点が表れる。今回は左下の隅に表示されている。
- 右上の画像の状態から フィルター → Seach... → Plot Selection Over Timeと打つ → 出てきたらEnterキーを押す → オブジェクトインスペクターの適用をクリックすると下の画像のように表示される。
- 下の画像に表示されているグラフはステップ毎のたわみや応力の関係を表したものである。
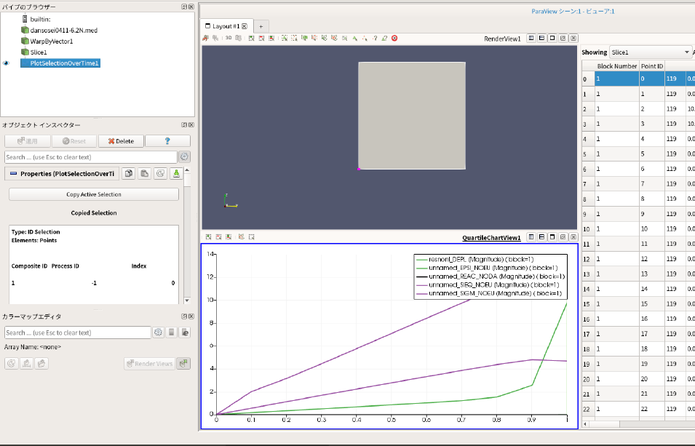
- 左側の上らへんに Showing という文字があると思うのでその右側を Plot Selection Over Time にすると下の画像のように表示される。この状態でCSVファイルに保存すればある1点におけるたわみや応力等の時間変化のグラフを作成できる。
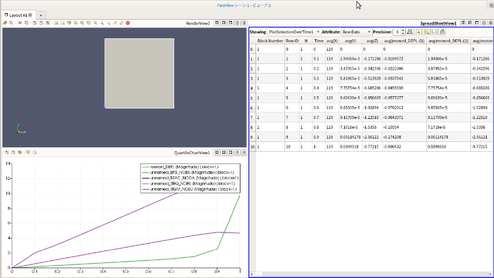
- 荷重は1.0sかけて指定した荷重をかけているわけなので0.1sごとに指定した荷重の10分の1ずつ加わっていることが分かる。たわみを知るにはDEPL(変位量)の部分を見る必要があり、今回の場合はz軸方向にたわむよう設定したためDEPL-(2)の数値を用いる。(x軸方向なら0, y軸なら1)
- ここから荷重ーたわみ曲線の表を書くと以下のような表ができる。今回は梁モデルにかけた面載荷を6.2Nとした。(軸方向:x , たわみ方向:z)
| たわみ [avg(resnonl_DEPL (2))] | 荷重 (N) |
| 0 | 0 |
| 0.173432 | 0.62 |
| 0.346841 | 1.24 |
| 0.520225 | 1.86 |
| 0.693586 | 2.48 |
| 0.866922 | 3.1 |
| 1.04111 | 3.72 |
| 1.23941 | 4.34 |
| 1.55289 | 4.96 |
| 2.58588 | 5.58 |
| 9.82065 | 6.2 |
- 直応力-直ひずみのプロット(今回は直ひずみが最大となった点を先に探しそこから直応力とのグラフを作成した)
- Paravis上で○軸方向の直応力を見たい場合はSIGM_NOEUのSI○○を、○軸方向直ひずみの場合はEPSI_NOEUのEP○○をそれぞれ選択すると見ることができる。(○には\( x \), \( y \), \( z \)のどれか一文字が入り、同時に2つ見ることは不可能。)
- 軸方向直応力が最大となる点はParavisでWarpByVectorを選択した状態でその上にあるEPSI_NOEUのEP○○を選択すると赤と青のグラデーションで表示された分布図(?)が表示される。直応力も同様の手順。
- モデルの中で特に色の濃い箇所を探し、見つけられたらその部分をSliceして1点を時間経過ごとにcsvファイルとして抽出する。その方法は上記に記載。
- csvファイルを開いたら直応力はSIGM_NOEU, 直ひずみはEPSI_NOEUなので知りたい軸方向の情報を取り出してグラフを描く。下の表は軸方向:\( x \) とした梁モデルにおけるステップ毎の直応力-直ひずみの関係である。
| 直ひずみ [avg(unnamed_EPSI_NOEU (0))] | 直応力MPa [avg(unnamed_SIGM_NOEU (0))] |
| 0 | 0 |
| 0.000163705 | 39.2887 |
| 0.000327421 | 78.5892 |
| 0.000491148 | 117.901 |
| 0.000654883 | 157.224 |
| 0.000818626 | 196.558 |
| 0.000993534 | 233.027 |
| 0.0012371 | 247.027 |
| 0.00184441 | 252.747 |
| 0.00502795 | 264.78 |
| 0.0283099 | 291.326 |
- 相当応力(ミーゼス応力)―相当ひずみのプロット
- 相当応力はParavis上であればSIEQ_NOEUのVIMSで確認することができ、1点を時間経過毎にとったcsvファイルではSIEQ_NOEU (0)がそれにあたる。
- 相当ひずみはParavis上であればEPSI_NOEUのMagunitudeで確認することができ、1点を時間経過毎にとったcsvファイルではEPSI_NOEU (Magunitude)がそれにあたる。
- 相当ひずみは一応計算式が存在し\( x \)~\( z \)の直ひずみと\( xy, yz, zx \)のせん断ひずみの計6つの値を用いることになるが、計算で求めた値とEPSI_NOEU (Magunitude)の値は殆ど同じになる。
- 下の表に相当応力―相当ひずみの関係を示しておく。
| 相当ひずみ[avg(unnamed_EPSI_NOEU (Magunitude))] | 相当ひずみ[計算式から求めた値] | 相当応力MPa [avg(unnamed_SIEQ_NOEU (0))] |
| 0 | 0 | 0 |
| 0.000177244 | 0.000141138019653 | 38.8404 |
| 0.000354521 | 0.000282331197335 | 77.6913 |
| 0.00053183 | 0.000423531884191 | 116.552 |
| 0.000709169 | 0.000564776351602 | 155.424 |
| 0.000886536 | 0.000706053036519 | 194.304 |
| 0.00107728 | 0.000858495560505 | 228.822 |
| 0.0013591 | 0.001089542714271 | 237.896 |
| 0.00208858 | 0.001690454081658 | 237.894 |
| 0.00598366 | 0.004877997525343 | 237.911 |
| 0.0348534 | 0.028444256381814 | 238.12 |
- 曲げモーメントが最大となる断面の軸方向直応力を各荷重レベルでプロットし応力の三角形分布を確認し、上下縁から徐々に降伏が入って最終的に全塑性の状態になるか。
- 曲げモーメントが最大となる所は片持ち梁のM図を想像すると分かるだろう。その部分でスライスし軸方向直応力 = SIGM_NOEUのSI○○ の分布を見る。(○には\( x \), \( y \), \( z \)のどれか一文字が入る)
- ここから三角形分布を確認していくが、その前にウォーミングアップとしてSliceした面においてどの点が一番直応力のかかっている点なのかをスカラーで可視化していく。
→パイプブラウザーでSliceを選択した状態で フィルター → Seach... → Warp By Scalar と打つ → 出てきたらEnterキーを押す → オブジェクトインスペクターにあるScalarsを "unnamed_SIGM_NOEU_SI○○"にScale Factorを1から0.001~0.1程度にそれぞれ書き換えて適用をクリックすると下の画像のように表示される。
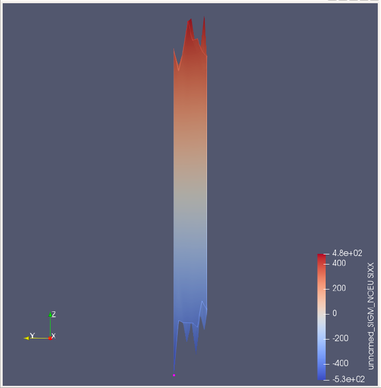
- このように直応力をスカラーで表示させることでどの点にどのくらいの応力がかかっているかひと目で分かる。中心から一番離れている点を選択すれば直応力と荷重のグラフを作成できる。
- 上の画像から直応力最大点(付近)を点を選びその直応力と荷重の関係表を以下に示す。
| 荷重(N) | x軸方向直応力(MPa)[avg(unnamed_SIGM_NOEU (0))] |
| 0 | 0 |
| 0.62 | 45.7055 |
| 1.24 | 91.416 |
| 1.86 | 137.131 |
| 2.48 | 182.851 |
| 3.1 | 228.574 |
| 3.72 | 267.812 |
| 4.34 | 289.333 |
| 4.96 | 304.662 |
| 5.58 | 347.945 |
| 6.2 | 529.847 |
- 次にパイプブラウザーでWarpByVectorを選択した状態で Warp By Scalar を選択 → オブジェクトインスペクターにあるScalarsを "unnamed_SIGM_NOEU_SI○○"にScale Factorを1から0.001~0.1程度にそれぞれ書き換えて適用をクリックすると下の画像のように表示される。


- 上の2枚からは直応力の三角形分布を確認できることに加えて梁が降伏したかどうか赤と青のグラデーションで判別することもできる。今回は梁の中心部分がまだグレーの状態にあるため全塑性状態になったとは言えず、さらに面載荷を増やす必要がある。
4/9†
2/18†
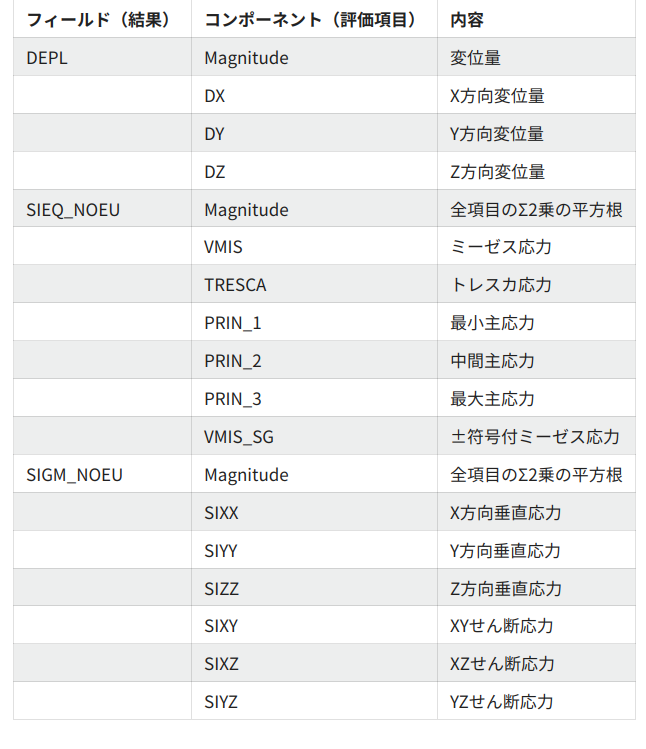
- SS400について
- ヤング率…205\( GPa \)
- 降伏応力…235\( N/mm^2 \)
- 弾塑性とは
- 加えた力が降伏応力に満たない場合は物体が元の形に戻る弾性の性質を持ち、
加えた力が降伏応力を上回る場合は物体が元の形に戻らなくなる塑性の性質の両方を持っている性質のこと。
また弾塑性体は上記の性質を持つ物体の事を呼ぶ。
- ミーゼス応力
- ある物体にかかる応力が複数ある場合(x軸方向に垂直応力が、z軸方向にせん断応力がかかっている等)においてせん断エネルギーが1軸の応力と同じになる応力のこと。
式は応力の差を2乗した和を2で割り、各方向のせん断応力の2乗の和に3を掛けたものを足して√をつけたもので表される。
- また式が平方根で表されているためミーゼス応力は引張や圧縮に関係なく常に正の値をとる。また方向の情報を持たないスカラーである。
2/7†
- 弾塑性班
- 鋼材の長方形断面の梁(想像しやすい大きさ)の片持ち梁と単純梁を曲げる
- 軸方向:\( z \), たわみ方向:\( y \)
- SS400ぐらいのヤング率と降伏応力で弾塑性解析の設定
- 載荷点での荷重、たわみのプロット
- 軸方向直応力が最大となる点での直応力-直ひずみのプロット(降伏点付近で折れ曲がるか)
- その点での相当応力(ミーゼス応力)―相当ひずみのプロット(上記との違いは)
- 曲げモーメントが最大となる断面の軸方向直応力\( \sigma_{zz} \)を各荷重レベルでプロット(\( yz \)の2次元と、できれば3次元も)し応力の三角形分布を確認する
- 上記の三角形分布において、上下縁から徐々に降伏が入ってきて、最終的に全塑性の状態になるか。
- 上記を確認できたら、I型断面とかの三角形分布や全塑性が、どういう応力分布になっているのかを確認。
- やること
- SS400のヤング率と降伏応力を調べる
- salome上でモデル作成
- 荷重条件を変化させながらたわみを測定
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)