�ܼ�
2018ǯ��
- ����13:00���饼�ߡ�3ǯ�ϻ��ü�ͳ��
- ����14:30������¤��˼�½���3ǯ��ɬ����
- 11/23(��)�Υ��ߤϵ٤�
3ǯ��
2/1(�յ٤ߤβ���)
- 10mm$\times$10mm$\times$100mm���¤ξ�1mm�Ȳ�1mm��ݺ���Ѥ��ơ�����ߤ��
- �ݺ�ϥ��Ψ��206GPa, �ݥ������桧0.3
- �ں�ϰ������ΤȤ���Ʊ������
- ��«���Ⱥܲپ���Ʊ������Ω����˹�����������
- �����$E_{��}I_{��}+E_{��}I_{��}$���ᡢ�ƥ��⥷�����¤Τ���ߤȽ����¤Τ���ߤ����
- Salome-Meca�Τ���ߤ���Timoshenko������¤Ȥɤ줯�餤�礦�����岼��Ǥ���ΤǶ��������ɥ��å��¤Ǥϡ��������ѷ������������Τ��ष����Ĺ�����Τ��ˤĤ��ƹͻ�
- ������ˡ�����Ϸ�̡��ͻ����Ƥ�$\TeX$�����̻������ץ�������ǤޤȤ�롣
1/11(����)
- ���ޤǤ����и����Υ���դ��������̤��ƺ��ľ��
- �ǽ�˺�ä��һ����¤�comm�ե���������ݡ��Ȥ��Ƥ���
- �ǽ�˺�ä��һ����¤�Ʊ��
- ������:10mm$^2$
- ��:100mm
�ǡ��ʤ�٤��������礭���һ����¤��롥
- ���̤�100mm$^2$�Ǥ���С������ϼ�ͳ��I���Ȥ�Ȣ���Ȥ��߷��Ȥ���
- Salome��������Ѥ�Ĵ�٤�ˤϡ�Geometry�Υ��֥������ȥ֥饦�������̤Υ��֥�������(Face_3�Ȥ�)�������ַ�¬�ץ�˥塼�Ρִ��ܥץ��ѥƥ��פ����֤ȥ����ե����ΤȤ��������Ѥο��ͤ��Ф�ʤ��֤��
- ���������̤ϡ��ǽ�˺�ä��һ����¤����̤�Ʊ����ɸ��(xy�̤Ȥ�yz�̤Ȥ�)�˺��
- 1/25�ϡ���ƣ���Ժߤ�������ʬ�Ǻ�ä��һ����¤ˡ�comm�ե�������ɤ߹���ǡ��ٽŤ�ݤ��Ƥ���ߤ���Ǥ��뤫�Ƽ���äƤߤ롥
12/21(4ǯ��M2�����ȯɽ)
12/21��4ǯ��M2�����ȯɽ�ʤΤǥ��ߤϵ٤ߡ������1/11(��)������3ǯ���ϡ����̻������ץ�������(sibup2.tex)��Ȥäơ�����ޤǥ��ߤǹԤä��½������Ƥ�Ƽ��ޤȤ���ȤϤ��뤳�ȡ�2�ڡ����ʾ�ǹ���ʤ�)��
12/14(����)
Salome-Meca�Υ�å���ޤʤɤ�GIMP�ǥ������åȤ���eps�ե�����˥������ݡ��Ȥ��������sibup2.tex��Ž���դ��롣
12/7(����)
gnuplot�οޤ������������ä���LaTeX�˼�����(PS/LaTeX��)�Τ�����ǡ�
���ޤ������Ƥ������и����Υ���դ˼��䥿���ȥ�������������ä��ơ�zu.tex�˼����ࡣ
pdf���������̤�wiki��Ž���դ��������ϡ�A4�Τޤޤ��ȤǤ����ʤ�Τǡ���1�示�ĤȤ����������åȤ���Ž���դ���ʤ���ϡ���äƤߤ����ͤ����Ǥ������ɡˡ�
11/30(����)
LaTeX �� XHTML ����˳ؤܤ�
��web1w.tex����web4w.tex�ޤǤ�����ƥ���ѥ��뤷�������ǻȤ��Ƥ���$\TeX$���ޥ�ɤν����˴���롣
11/16(����)
- $z$�����¼������Ȥ����硢$E_{x}=E_{y}=\frac{E_{z}}{25}, G=\frac{E_{z}}{15}$��ľ������������DzƤߤ�
- �����إ�ǥ�ϡ��轵����Ω����˹�������ƹ�«���Ⱥܲ������ߤ������
- �ƥ��⥷�����¤�������$v=\frac{P\ell^{3}}{48E_{z}I}+\frac{P\ell}{4kGA}$���Ф������и�������롣
- Ĺ�������̤Τ�������������$k=\frac{5}{6}$
- ���ǿ������и����δط���դˤ���´������˥��å�
11/9(����)
- ��Ū���¥�ǥ�ȶᤤ���ˤ��뤿��ˡ���Ω�̾������«�����ܲ٤�������
- ʪ���������������˺ܲ٤���ȥ��顼���Ф�褦�ʤΤǡ���Ω��������֤ˡ�
�⤵0.1mm, Ĺ��0.2mm, ���Ԥ�10mm��ľ���Τι������������̤���Ω�̤˹礦�褦�ˡ�
- �����ơ��������̤ο���������˱�ä����ܲ٤��롣
- ��«���ˤĤ��Ƥ⡢Ʊ�ͤ�ľ���Τι�������ʾ��̤���Ω�̤ȹ礦�褦�ˡˡ�
���ξ��̤ο���������˱�äƹ�«�����ñ��ٻ���
- ����Ǥ����ȷ��Ǥ���褦�ʤ顢
- ĥ��Ф�������¤ˤĤ��ơ�
��å���Ĺ��6, 5, 4, 3, 2, 1.5, 1.3, 1, 0.7, 0.5�ξ���������Ѱ̡ʺܲ���ξü��ʿ�ѡˤȼ�������и��������ǿ��δط���ץ��å�
- ĥ��Ф����ʤ��¤ˤĤ��Ƥ�����˹������Ʊ�ͤη���ξü������«��ʬ��ɽ�̤˽ФƤ���Τǹ�����ɬ�פϤʤ���
11/2(����)
- ���������Τǥ��ѥ�100mm��Ĺ120mm��ñ���¤��ǥ벽����
����β����Ʊ�ͤ˥�å���Ĺ��8, 7, 6, 5, 4, 3, 2, 1.5, 1, 0.5�ξ���
������Ѱ�(�����ߤ�ʿ�ѡˤ�����롣
- ���ǿ����ˡ�$\frac{P\ell^{3}}{48EI}$���Ф������и�����ļ��ˤ���gnuplot������������դ��С��˥��åפ��Ƽ�ʬ��´���ڡ�����Ž���դ��롣
- Ĺ�����礦��100mm�Υ�ǥ�������������ξü��¦������«����ñ���¤ˤĤ��ơ���å���Ĺ��1mm�η��롣ξü��10mm���Ĥ�ĥ��Ф��Τ�����Ȥʤ����Ȥǡ��ɤ���������˰㤤���Ф뤫���ɤ��餬$\frac{P\ell^{3}}{48EI}$�˶ᤤ�ͤˤʤ뤫��������ͳ�ˤĤ��ƹͻ����롣
10/26(����)
- ��å���Ĺ��0.5, 1.5, 3,5,6,7���ɲä��ơ�ɽ���ľ����
- ���ǿ����Ѱ̤Υ���դ�����ľ�������åץ����ɤ��ơ�wiki��Ž���դ��롣
10/19(����)
- Salome-Meca���һ����¤����ͳü4���ߤ��Ѱ̤�ʿ�Ѥ����
- ��å����Ĺ��local length=1, 2, 4, 8�ξ��ˤĤ���Ʊ�ͤ˷�
- ���줾��Υ�å���Ĺ���ξ������ǿ����⤹��
- �����Ƽ���´�������ɽ�ˤ��ƤޤȤ��
- ����ǵ��һ����¤��Ѱ̤���Ӥ���
- ü�����顢UNIX���ޥ�ɤǼ�ʬ����¸����Salome�Υե����뤬�ɤ�����¸����Ƥ��뤫���ǧ���Ƥ�����
| ��å���Ĺ�� | ���ǿ� | ��ü�Ѱ� | ���и���($\frac{salome-���}{���}$) |
- �����6GPa
- �ݥ������桧0.4
- 10mm$\times$10mm$\times$100mm
- ��ü�ٽš�100N
10/12�ʲ����
- ��¤��wiki��´����������
- ���å������ס��轵�ޤǤǤ���褦�ˡ�
���å������פ�����
- abcdefghijklmnopqrstuvwxyz
- ABCDEFGHIJKLMNOPQRSTUVWXYZ
- aBcDeFgHiJkLmNoPqRsTuVwXyZ
- AbCdEfGhIjKlMnOpQrStUvWxYz?
- 3.1415926535(5��)
- 1.7320508075(5��)
- �ʾ��3ʬ�������ɸ�ˡ�
ABCDEFG�ʤɺ����ʸ�����ǤĤȤ��ϱ���ξ��ؤ�
SHFT����������
HIJKLMN�ʤɱ����ʸ�����ǤĤȤ��Ϻ���ξ��ؤ�
SHFT���������롣
����Ū���Ҽ��SHFT��ʸ����������Ĥ�����Ȥ���
���ȤΤʤ��褦�ˡ�Enter������(�����ž������)����ξ��ؤǡ�
�ؤ��Ϥ��¤���Ӥ���ʬ�ϴ��ˤ��äĤ������֤ǻش���ζʤ����Ф��ȼ��β�ž�Τߤ�
��ͳ�٤�Ȥ��������Ӥ�����夲�ʤ��褦�ˤ��롣
ã����ɸ
- ������������ľ�����¤�3D��ǥ벽����Salome-Meca�Ǥ���ߤ���ơ� ��������
- ���ǿ������и����δط���gnuplot�ǥե�ղ�
- ������������ľ�����¤�3D��ǥ벽����Salome-Meca�Ǥ���ߤ���ơ� ��������
- �ݺ���ں�ι����¤�3D��ǥ벽����Salome-Meca�Ǥ���ߤ���ơ� ��������
- �⤷;͵������С������������δ�����3D��ǥ벽������������Ϳ���ư���ĥ��Τ��������Ƿ��ʥ���դ�������
- �����η�̤�LaTeX�Ȥ������ǥġ����´���������ˤޤȤ�ơ� ��¤��˼�½�������ʪ(pdf�ե�����)�Ȥ������
´���ơ���
- CLT�ζʤ������ʤ���줿��δޤ�ˤȤ���β���(Salome��Marc)
- �饰������塼��Ϣ�뤵�줿CLT�ȥ���Ȥΰ���ȴ����Ȥ��β���
- I��ˤΤ���CLT���Ǥ��ɸ����Ĥ��Ƥζʤ���Ȥ���β���(Salome��Marc)
- �����Ф�CLT����I�嶶�Υȥ�å��ܲٻ�Ȥ��β���
- �ץ쥹�ȥ쥹��Ȣ�嶶�β��ϡ����Ӥ�2�ܥå��������ס��Ѥ������α��ϡ�
- �����ޤ�����ΤФ������ޤꤿ���ߤ䤹���ȼ�Ω���䤹���δط���
5/7
�ե����ȥ�������β���1����3�ޤǤ��äƤߤ�(����)��
4/23
- vi�λȤ���
- vi�ǡ�2018ǯ�Υ�����������
- vi�ǥѥ�����λ��ѷ����(6�ʰʾ�)
- vi�����ܸ��Ŭ����ʸ�ϡ������Ȥ����ˤ��������
1��
�� �� �� �� �� �� ��
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30 31
2��
�� �� �� �� �� �� ��
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28
1
/ \
1 1
/ \ / \
1 2 1
/ \ / \ / \
1 3 3 1
4/17����
����
- ���å������פϤ����ȤǤ���褦�ˡʤ����Ǥʤ����轵��vi�Ƕ�ϫ�����
- ������UNIX���ޥ���ϤҤ��̤�Ȥ���褦�ˤʤ롣
- echo, >, >>, cat ���ޥ�ɤ�Ȥä�2018ǯ�٥����������롣
���
echo "�� �� �� �� �� �� ��" >4gatu
echo " 1 2 3 4 5 6 7" >>4gatu
echo " 8 9 10 11 12 13 14">>4gatu
�ߤ����ˤ��ơ�5gatu, 6gatu,.....,1gatu, 2gatu, 3gatu �����
cat 4gatu 5gatu 6gatu .......3gatu >cal2018
cat cal2018�dz�ǧ
2017ǯ��
- ����϶���13:00����
- 1���֤ο�Ľ�����ȼ���1���֤ηײ�����
- 14:00������¤��˼�ʤΤǡ��ѥ������3ǯ���˻Ȥ碌��ȤȤ�ˡ��Թ�ε����¤ꡢ3ǯ�������Salome2017��
- Ubuntu��kouzou�桼������¾��souzou�桼�������ꡢ3ǯ���ˤϤ������Ȥ碌��
8��ʹߤ�ͽ��
- 8/22(��)13:00��Ľ��ǧ
- 9/22(��)13:00���ȯɽ
- ´����Ʊ��������´�����ס�ȯɽ���饤�ɤ������
- ´����Ʊ��������ʬ(6ʬ���ä������ˤ�ȯɽ��
- ´�����פϡ�
- �������� ���ܥե�����Linux��UTF-8��
9/15��20�ˡ����������ڤȤΥ��եȥܡ�������ĤǤ���ޤ���
�����Ǥ���¤껲�ä��Ƥۤ����Ȼפ��ޤ���
���������ڤζ����������������Ȥθ�ή����Ū�ʤΤǡ�
���եȥܡ���ϤǤ��ʤ��Ƥ�褯�ơ�
���θ�κ��Ʋ���Ū�Ǥ���
5/22(���̲���)
- ��Į��5/15�β���ޤǤǤ���褦�ˤ���
- ��¼���ں�ȹ��ĤΥ���ɥ��å��¤��ǥ벽���ƲƤߤ�
- ���͡�Ŭ����Ω�Τ�G-code���������3D�ץ���ǰ������Ƥߤ�
5/15
- gFTP��k2�����С���str�����С��˥����������ƥե�����Υ��åץ����ɤ����������ɤ��Ǥ���褦�ˤʤ�
- 2017�ǥ��쥯�ȥ����˼�ʬ�ѤΥǥ��쥯�ȥ��Ĥ���
- ����η���̤Υڡ������ɽ���ǽ���
- �����������ˤ���Ʊ�������äƤߤ�
- $E_{zz}=6$GPa, $E_{xx}=E_{yy}=\frac{E_{zz}}{25}$
- $G_{xy}=G_{yz}=G_{zx}=\frac{E_{zz}}{15}$
- �ݥ�������
- ��¼�η��
- ���ͤη��
5/8
- 10mm��10mm���̤γѺ�ʥ��Ψ��6GPa, �ݥ������桧0.3�ˤ�ñ���¤Τ���ߤ����
- ������($\frac{P\ell^{3}}{48EI}$)���ƥ��⥷������($\frac{P\ell^{3}}{48EI}+\frac{P\ell}{4kGA}$)���Ф������и�������롣
- FEM�Τ���ߤ�paravis������κ����Ѱ̤�
- �������ʤ������ϡ���������������$G=\frac{E}{2(1+\nu)}$
- Ĺ�������̤Τ�������������$k=5/6$
- �ٽŤ��̲ٽŤ�100N.
- ���ѥ�Ĺ���ϡ�3�ͤǡ�100mm, 200mm, 1000mm��ʬô��
- ����ʬ��ϡ�Length��8, 4, 2, 1
- 1������(linear)��2������(quadratic)
4/24����
�ե����ȥ�������β���1����3�ޤǤ��äƤߤ�(����)��
4/17����
����
- ������UNIX���ޥ���ϤҤ��̤�Ȥ���褦�ˤʤ롣
- vi�ǡ�2017ǯ�Υ�����������
- vi�ǥѥ�����λ��ѷ����(6��)
1��
�� �� �� �� �� �� ��
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30 31
2��
�� �� �� �� �� �� ��
1 2 3 4
5 6 7 8 9 10 11
12 13 14 15 16 17 18
19 20 21 22 23 24 25
26 27 28
1
/ \
1 1
/ \ / \
1 2 1
/ \ / \ / \
1 3 3 1
2016ǯ��
6/13�ޤ�
- ���Ϥ�ļ�(z)�ˤ��ƽ�����
- ����(z=0)��3�����ץ��åȤ˰��˥ץ��åȤ���
- ľ�������Ǥǡ�����ü����1���ǤȤʤ�����̤α���ʬ�ۤϡ��ɤ줯�餤�Ѥ�뤫
- �¤ο���������̤α���ʬ�ۤϤɤ����ʰʾ��3�ս����ӡ�
- ���$\sigma=\frac{M}{I}y$�Ȥɤ줯�餤�礦��������ǵ�ޤ��̤�3�����ץ��åȤˤ��碌�ƥץ��åȡ�
6/6
gnuplot��ư����
set term png
set output 'gazou.png'
splot 'data' w l
- eog gazou.png��gazou.png���ǧ��
- gftp��str��gotouhan�˥�������
- FTP��Preference��FTP��Passive�Υ����å����Ƥ���
- ��¦����������ʼ�ʬ��PC�ˡ���¦�������С�
- �����С�¦��public_html���椬�����־�˸�������Ƥ�
- public_html/j2016/����˳Ƽ��Υǥ��쥯�ȥ��Ĥ���ʺ����٤��ʤ���С�ï�Υǥ��쥯�ȥ꤫�狼��褦�ʥǥ��쥯�ȥ�̾�ǡ�
- ���ä���ä�PC��β����ե������֢��פ�å����ơ������С�¦�μ�ʬ�Υǥ��쥯�ȥ�˥��åץ�����
- str�����Ф�public_html�β��ϡ�http://www.str.ce.akita-u.ac.jp/~gotouhan/���б����Ƥ��롣
- �����顢gotouhan/j2016/gotou/��������ä������ե�����ϡ��㤨�С�
�ߤ����ˤ��β����ե�����Υѥ����˽���ȡ�
��ưŪ�˥��Ž���ơ�������Ž���դ����롣
5/9
�礭�����ٽš�Ŭ���ǡ��һ����¤�Salome�Ǻ�äơ��������Ⱥܲ������äơ�
��å���ʬ�䤷�ơ��ܲ٤��ơ��Ѱ̤�뤫��
5/16
10mm��10mm���̤γѺ�ʥ��Ψ��6GPa, �ݥ������桧0.3�ˤ��һ����¤�
�����¡��ƥ��⥷�����¤��Ф������и�������롣�ٽŤ��̲ٽŤ�100N.
Ĺ���ϡ�7�ͤǡ�50mm, 100mm, 200mm, 400mm, 800mm, 1000mm, 2000mm��ʬô��
����ʬ��ϡ�Length��16, 8, 4, 2, 1
5/23
�轵�β���ǡ����������Ǥ�Ω�������ǤΤ��줾����Ф����������Ǥ�2�����ǤΤ��줾��4�̤������Ƥߤ롣
Ω�������Ǥ�����Ĺ���ϡ�2mm, 1mm, 0.5mm
4/25
����
�ե����ȥ�������β���1����3�ޤǤ��äƤߤ롣
���ޤ�
scratch�ȡ��뤷�������
- �����ƥࢪ�����ƥ������Synaptic���ѥ��������
- scratch�Ǹ���
- scratch(easy to use programming environment for ages 8 and up)�˥����å������좪���ȡ�����ꢪ�ޡ���
- Ŭ�Ѣ�Ŭ��
- ���ȡ��뤬��λ�����颪�ե����뢪��λ
- ���ץꥱ������ץ�����ߥ�Scratch �ǵ�ư
4/18����
����
- ������UNIX���ޥ���ϤҤ��̤�Ȥ���褦�ˤʤ롣
- vi�ǡ�2016ǯ�٤Υ�����������
- vi�ǥѥ�����λ��ѷ����(10��)
4��
�� �� �� �� �� �� ��
1 2
3 4 5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23
24 25 26 27 28 29 30
5��
�� �� �� �� �� �� ��
1 2 3 4 5 6 7
8 9 10 11 12 13 14
15 16 17 18 19 20 21
22 23 24 25 26 27 28
29 30 31
1
/ \
1 1
/ \ / \
1 2 1
/ \ / \ / \
1 3 3 1
4/11����
�ѥ���������
- ���ܸ�/Ⱦ�ѱѿ����ڤ��ؤ���̵�Ѵ������ʺ��ƻء�
- ���ԥڡ�������å������ơ�������ܥ����Ž���դ�
�֥饤��ɥ��å�������
- abcdefghijklmnopqrstuvwxyz
- ABCDEFGHIJKLMNOPQRSTUVWXYZ
- aBcDeFgHiJkLmNoPqRsTuVwXyZ
- AbCdEfGhIjKlMnOpQrStUvWxYz?
- 3.1415926535(5��)
- 1.7320508075(5��)
- �ʾ��3ʬ�������ɸ�ˡ�
ABCDEFG�ʤɺ����ʸ�����ǤĤȤ��ϱ���ξ��ؤ�
SHFT����������
HIJKLMN�ʤɱ����ʸ�����ǤĤȤ��Ϻ���ξ��ؤ�
SHFT���������롣
����Ū���Ҽ��SHFT��ʸ����������Ĥ�����Ȥ���
���ȤΤʤ��褦�ˡ�Enter������(�����ž������)����ξ��ؤǡ�
�ؤ��Ϥ��¤���Ӥ���ʬ�ϴ��ˤ��äĤ������֤ǻش���ζʤ����Ф��ȼ��β�ž�Τߤ�
��ͳ�٤�Ȥ��������Ӥ�����夲�ʤ��褦�ˤ��롣
2015ǯ��
- �ѥ����ߡ�����14:30
- �Ѹ쥼�ߡ�����13:00�ʤ��Ф餯�ϥѥ����ߡ�
6/1����
����(6/22�ޤ�)
�ʲ��ξ��Υ�ǥ��Salome�Ǻ������롣
FEM�Ѥι�«�����ܲ������äƤ�����
��å���κ٤�����Ŭ���ˤ��ơ�
���ѥ�100mm��ñ��ٻ���������������ܲ٤βٽž�������ơ�
aster�DzƤߤ롣
- �߷��
- ���ѡ�12000mm$^3$����
- ���ѥ�100mm
- �����2.84GPa
- �ݥ�������:0.313
- �ٽ�:1000N/�� (���ٽŤ�ñ�������ͤˤʤ뤫��)
- �ºݤˣ�D�ץ���Ȥ��Ǻ�äƲٽŤ����Ƽ¸�������ˡ�Ĺ�������礦��100mm���ȼ¸�����֤��ʤ��ʤä��㤦�Τǡ��֤���褦�˺�äƤ�������
- �㤨�С�ξü��10mm���餤���Ф��Ƥ����Ȥ�
- ���漼�Υۥ磻�ȥܡ��ɤ˳����Ƥ���ΤǤ��Υ������
- ñ��ٻ�����ܲ�
- ��«����FEM�Ǥ�����«������������ʶ���ˤ�����褦��
- �ܲ�����FEM�Ǥ����ܲ٤�����10mm���٤�ɳ������褦��
| ���� | ����(mm$^3$) | �����(mm) | ����$\frac{P\ell^{3}}{48v}$ | ������ʹ���/���ѡ� | ���ǿ� |
| ���� | 11956.7 | 0.73 | 28538813 | 2387 | 80404 |
| ��ƣ | 11276 | 1.16 | 17959770 | 1593 | 32705 |
| ���� | 11520 | 1.06 | 19654088 | 1706 | 128687 |
| ���� | 11302 | 23. 1 | 1301348 | 115 | 35491 |
| ��¼ | 12000 | 2.395 | 8698678 | 725 | 27151 |
| �ⶶ | 11952 | 1.25 | 16666666 | 1394 | 91074 |
| �ظ� | 12000 | 1.78 | 1170120 | 975 | 14536 |
| ���� | 12000 | 3.02 | 6898455 | 575 | 9567 |
| ��ƣ | 10682 | 2.64 | 13636363 | 1276 | 123951 |
| ��ƣ | 10920 | 3.82 | 7232633 | 662 | 175577 |
�����ǿ���Mesh�ڤä�����Volumes���ͤǤ�


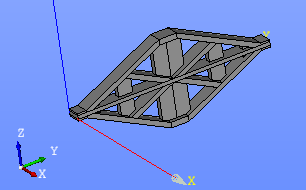

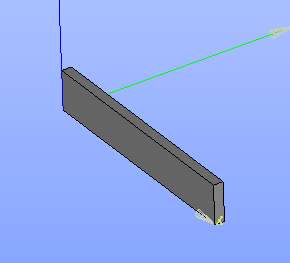
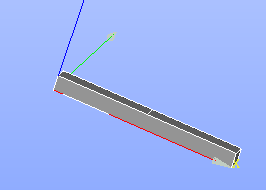
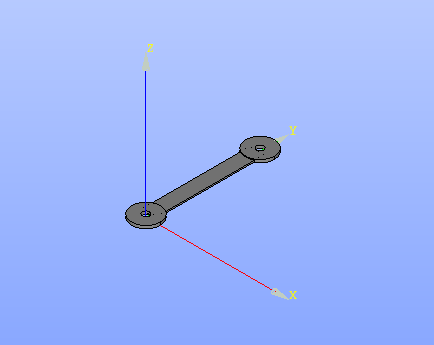
- ��ΤŤ��ꥻ�����ѿ�������ΤŤ��ꥻ������Ф��Ƥ���(�Ƽ�)
5/25����
- code-aster�δ���Ū�ʻȤ���������
- aster�ǡ���������ʪ�ΤȤ���ʪ���͡���������������
- E,��,��«���,�ٽŤμ��������,�ٽŤ��礭����comm�ե�����dz�ǧ
- �ٽŤμ����(������֤�)�̺ܲ٤���ܤȤ��ơ�����ͤ����ܲ٤ޤǻ��
- Eficas(aster�ˤĤ��Ƥ��뵡ǽ��GUI)�ϻȤ鷺��vi���ޥ�ɤ��Խ�
- ��������mess�ե�����Ǥ��ä�į�
- ��̤ϡ�post-pro�Dzٽ������Τ����(����դ�ɽ��)�ȥߡ��������Ϥ�
����
- Ŭ�����һ����¤���
- aster����ü�Τ���ߤ������
- ����ơ�aster�η�̤���٤�
5/18����
- compound�ǿ������
- mesh�ǿ����ڤ�
- partition�ǿ�����ڤ�
����
- ��Ŭ�����һ����¤�Ĥ���(�������ϵ��ˤ��ʤ��Ƥ������)
- �������̤ȹ����ʤȤ����˺ܲ���(��)����
- geometory�Ǥ��ˤ�
- ������å��Ρ�criate group�פȤ�����new��entity�פΡ�explode�פȤ����ġ�
- �����¤βٽ�����ϡ�����ٽ��(��ñ��������)
- �ܲپ�ﭡ���������Τˡ���ʬ�۲ٽ�(N/m^2)����
- �ܲپ�ﭢ������ü�ξ��̤˺ܲ٤��뤿��ξ������̤���(partition��criate group)����������ü����ٽ�(N/m^2)����
- �ܲپ�ﭣ����ü¦�̤ˡ���ü����ٽ�(N/m^2)����(�ٽ����������)
- �ܲپ�ﭤ���¤Υ��å��ˡ���ü����ܲ�(N/m)����(�ٽż��ࡦ�������ɲ��ѹ�)
- �ܲپ�ﭥ������ü�ˤ������ǤΥΡ��ɤˡ���ü����ٽ�(N)����(�ٽż��ࡦ�������ɲ��ѹ�)
- �ʤΤǡ����֤����ä��ۤ���������Ǥ����Ȥ����Τ⡢�������֤ϥ��ޥ�ɥե�����ν��������뤫�顣���֤ϡ�ɬ�פʤ����⡩
- ��Ŭ���˥�å�����ڤ�(������ˤ�äƤ⤤��)
- ���ʤߤ˸����̤Ⱥٰܲ��֤ϡ���å�����ڤä����Ȥˤ�Ĥ��뤳�Ȥ��Ǥ���
- mesh�ˤơ�������å��Ρ�criate group��
- �Ȥ��ǡ���롣���줫�顢���ٽŤ������Ȥ��ϡ�¿���ξ��ˤϡ���å���ʬ���Ǥʤ��ȤǤ��ʤ��Ȼפ��ޤ���
4/20����
- �ץ���������ˤĤ��ơ�������ץȷϡ�����ѥ����
- Fortran�ˤĤ���
- ���ꡧFortran������
�褯�ɤߤʤ��顢����1, ����2�ޤǤ��äƤ�����
4/14����
- vi�λȤ��� �Ф���
- ���ꡧ2015ǯ�Υ���������vi�ǽ�
4/9����
2014ǯ��
´���ơ���
- �ڶ��ϡ�3$\sim$4��
- �ڹ�������ȹ��Τ����ǵ�ư��1��
- �ޤ�桦3D�ϡ�2$\sim$3��
- ���1��
- �����������Ĥ��ڶ���1��
- ����¾��1��
5/15�ޤǤ˷��롣
5/26����
- mokuzai.f90�ͤˡ�ľ��������ǥ�ǥ벽�����ں�κ��������inp�ե�����˽���ǡ��ں���һ����¤�Ƥߤ롣
- �ƥ��⥷�����¤μ�$v=\frac{P\ell^{3}}{3EI}+\frac{P\ell}{kGA}$�ʤ�����$k=5/6$)�Ȥθ�����դˤ��Ƥߤ롣
5/19����
- gnuplot�ǥ���դ�������png�����˽��Ϥ��ơ�
- ������str�˥��åפ��ơ�wiki��Ž���դ���
����
- 3D�Ϥ��ꤿ���ͤϡ�3D�ץ������Υڡ�����
- Eden260V�ǻȤ�������ǡ�
- ���Ψ�����������ư�����ʤ�����
- �����Ȥϡ�
5/12����
- �����������ˤ��äơ�
- Salome��Ŭ����ľ���Ρ��������䤹��1cm��1m���٤γѺ�Ȥ�)��Ĥ���
- ��å���ʬ�䤷��unv���������
- c3d4unv.f90��Ȥäơ�CalculiX�����Ѥ�inp�ե��������
- �һ����¤ǡ���ͳü�˺ܲ�
- �������ں����٤Υ��Ψ������������
- ��å���ʬ�������������⡢��Ĺ����Ψ�����Ψ�����Ƥߤơ�
����ߤμ�($v=\frac{P\ell^{3}}{3EI}+\frac{P\ell}{kGA}$)�Ȥ����и������ɤ�
�Ѥ�뤫��ͻ�������̤�ɽ�ˤ��ơ��Ƽ���´������ˡ�
4/28����
4/22����
gfortran�Υ���ѥ���
gfortran -o hoge hoge.f90
������Fortran�����β���2�ޤǽ��ꡣ
4/14����
- ������UNIX���ޥ�ɤ�vi�λȤ�����Ф��롣
- ���ξ�ǡ��ʲ���Linux����ˤΥƥ����Ȥ�Ŭ���ʥե�������Ǥ����ࡣ�����ԥ�vi�������롣
- vi��Ȥ��Ȥ������������Ȥ鷺��hjkl�ǰ�ư����Τˤʤ��
- ���Ԥϡ��������Ȥ��ζ��ڤ�Τ����Ȥ��ǡ����ޤ������롣
- ���塢TeX�ʤɤΥġ����ʸ���Ȥ��ϡ����Ԥϵ����ޤ����Ȥʤ롣
4/10����
Linux�����
�ѥ���������
- ���ܸ�/Ⱦ�ѱѿ����ڤ��ؤ���̵�Ѵ������ʺ��ƻء�
- ���ԥڡ�������å������ơ�������ܥ����Ž���դ�
�֥饤��ɥ��å�������
- abcdefghijklmnopqrstuvwxyz
- ABCDEFGHIJKLMNOPQRSTUVWXYZ
- aBcDeFgHiJkLmNoPqRsTuVwXyZ
- AbCdEfGhIjKlMnOpQrStUvWxYz?
- 3.1415926535(5��)
- 1.7320508075(5��)
- �ʾ��3ʬ�������ɸ�ˡ�
ABCDEFG�ʤɺ����ʸ�����ǤĤȤ��ϱ���ξ��ؤ�
SHFT����������
HIJKLMN�ʤɱ����ʸ�����ǤĤȤ��Ϻ���ξ��ؤ�
SHFT���������롣
����Ū���Ҽ��SHFT��ʸ����������Ĥ�����Ȥ���
���ȤΤʤ��褦�ˡ�Enter������(�����ž������)����ξ��ؤǡ�
�ؤ��Ϥ��¤���Ӥ���ʬ�ϴ��ˤ��äĤ������֤ǻش���ζʤ����Ф��ȼ��β�ž�Τߤ�
��ͳ�٤�Ȥ��������Ӥ�����夲�ʤ��褦�ˤ��롣
���������´����������
UNIX���ޥ��
MATEü�����ơ�
- ls
- cd �ǥ��쥯�ȥ�̾
- mkdir �ǥ��쥯�ȥ�̾
- pwd
��¤��Ʊ�륦�������Ĺë���������ӽ��ꥹ�Ȥ�����
ubuntu�Υ��åץǡ��ȤˤĤ���
���åץǡ��ȡ��ޥ͡�����ǡ֤��Υ���ԥ塼�������ѤǤ��륽�եȥ��������åץǡ��Ȥ�����ޤ��פ�ɽ�����줿��硢
�֥��åץǡ��Ȥȡ���פ�å����ƥ��åץǡ��Ȥ�
���ȡ��뤷�Ƥ����Ʋ�������
''����������Ubuntu�ο���������'12.04.1 LTS'�����Ѳ�ǽ�Ǥ��פ�ɽ������Ƥ�����ϡ֥��åץ��졼�ȡפΤȤ����ϥ���å����ʤ��褦�ˡ�''
ubuntu��12.04�˥��åץ��졼�ɤ��Ƥ��ޤ��ȡ�CAE Linux�Υġ����Salome�Ȥ��ˤ�
ư���ʤ��ʤäƤ��ޤ��Τǡ����åץ��졼�ɤϹԤ鷺�ˡ�
���åץǡ��ȤΤߤ�Ԥ����ȡ�
2013ǯ������
- ����14:30����ѥ�����
- ����13:00����Ѹ쥼��
���߲����ڶ�(6/24�ޤ�)
- �����䥪�����ڶ����һ�����ǥ�ޤǤβ���ߤ����˲�
- ��«�Υ���դ䡢�����Υ���դ�Ƥߤ�
���߲���(6/17�ޤ�)
- salome���轵�β����Ʊ�����Υ�ǥ���äƥ�å�����ڤ�
- �����ccx��inp�ե�����ˤ��Ʒ����롣
- �轵�ߤ����˥���դ��
���߲���(6/10�ޤ�)
- �һ����¤η����ľ��
- �����ͤϥƥ��⥷�����¤Τ���ߤ������
- �����̤Ͻ�Ĺ������������Ĺ�Σ���
- ����ʬ���$nx=2\sim 10, ny=10\sim 40, nz=10\sim 500$
- nz�ޤ���ny���Ѱ̤ʤɤΥ���դ�gnuplot�������Ƥߤ�
- str�����С���gotouhan��gftp�ǥ�����������Ŭ���ʡ�̾�����¬�Ǥ���˥��֥ǥ��쥯�ȥ�������������դåץ����ɤ��ƳƼ���´�������Ž���դ���
- ���������Ͽޤ�����ʤ��Ƥ����Τǡ����������������
����Ž���դ�������
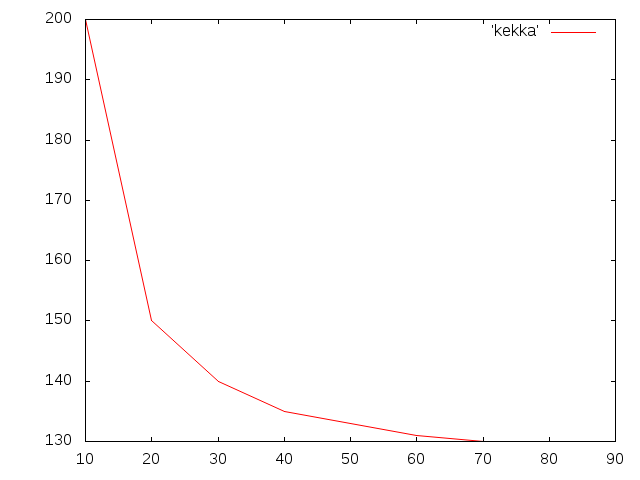
���߲���(6/3�ޤ�)
- ccxkataz.f90��Ȥäơ�(1���Ǥ��礭����1mm��꾮�����ʤ�ʤ�f9.3�ΤȤ������Ѥ��롢���ȲٽŤΤȤ�����ե����ޥåȤƤ��뤫��inp�ե�����βٽŤο����η�ʤ�����)
�����Ǥ����礭�����������һ����¥�ǥ���������ccx_2.3�DzƤߤ롣
- x������y������z����������ʬ����Ѥ��Ƥ��������$\frac{P\ell^{3}}{3EI}$�Ȥθ��������
- �����ϡ���ʬ�ǸǤ��������Ǥ����Τ����������㤨���ں�Ȥ��Ǥ������������Ȥߤʤ��ơ����Ψ������Ϳ���ʥ����ʤ�7GPa���餤�Ȥ��ˡ��ݥ�������ϤҤȤޤ�0.3�Ȥ��Ƥ褤��
���߲���(5/20�ޤ�)
������Fortran�����β���2�ޤǡ�
���߲���(4/15�ޤ�)
4/15�ʹߤβ���
�֥饤��ɥ��å�������
- abcdefghijklmnopqrstuvwxyz
- ABCDEFGHIJKLMNOPQRSTUVWXYZ
- aBcDeFgHiJkLmNoPqRsTuVwXyZ
- AbCdEfGhIjKlMnOpQrStUvWxYz?
- 3.1415926535(5��)
- 1.7320508075(5��)
- �ʾ��3ʬ�������ɸ�ˡ�
ABCDEFG�ʤɺ����ʸ�����ǤĤȤ��ϱ���ξ��ؤ�
SHFT����������
HIJKLMN�ʤɱ����ʸ�����ǤĤȤ��Ϻ���ξ��ؤ�
SHFT���������롣
����Ū���Ҽ��SHFT��ʸ����������Ĥ�����Ȥ���
���ȤΤʤ��褦�ˡ�Enter������(�����ž������)����ξ��ؤǡ�
�ؤ��Ϥ��¤���Ӥ���ʬ�ϴ��ˤ��äĤ������֤ǻش���ζʤ����Ф��ȼ��β�ž�Τߤ�
��ͳ�٤�Ȥ��������Ӥ�����夲�ʤ��褦�ˤ��롣
2012ǯ�ٸ��
- ���������ơ����ˤ�13:00����
- ���ˤ���¤��˼�½�����������Ǻ�Ȥ��뤳��
���������ڡ��漼�Ҳ�:M2�����Τˤʤäơ�����1�ԤϤʤˤ��Ƥ������ȡ�
�����ץ��ѥ�(7/28��)
2012ǯ��
�Ƶ٤ߤβ���
- ���桧salome��ǥ�ǥ벽�Ǥ�������䥫�åȤˤĤ��ơ���ƣ����ν����ˤʤ�äơ�
���̡���ĥ��ܲ٤������ΤФ�����������
- ���𡧤ޤ���ľ�����һ����¤�salome�ǥ�ǥ벽���ơ�CalculiX�Dz�ʼ������ӡˤ��Ȥ��ǧ���Ƥ��顢���ı�����salome�ǥ�ǥ벽����CalculiX�Dz�
- ��߷���������ڶ���ccxonsaito.f90�ǹ��Ĥ�G���Ѥ��ʤ���CalculiX�Dz�salome+CalculiX�ǹ��Ĥ��ں�Τ��äĤ���2������ľ���Υ�ǥ���ǥ벽���Ƥߤ롣
- �ʾ��´����������TeX�����ǤޤȤ�롣
- �ѥ����߷���14:30-16:00
- �Ѹ�FEM��������13:00-14:30
���������ڡ��漼�Ҳ�
- ���ä��ǿ����ʳ���Τߡ�
M2�����Τˤʤäơ�����1�ԤϤʤˤ��Ƥ������ȡ�
�Ѹ쥼��
- �з�(����Τߥ���������)
- ����(����Τߥ���������)
�ѥ�����
´���ơ���
- ���ĤȳѺ�α���(�¸���FEM����)
- �������ڶ�(���μ¸��ǡ����ν�����FEM����)
- �ޤ�湽¤(�����䥫�å�Ⱦ�����Ȥ�)��Salome�Ƽ�Υ�å���Dz����
- ������λ����Υ������ȥǡ����١�������
����
6/25�ޤ�
- Ŭ���ʥ���դ�������$\LaTex?$�˼�����
- �㤨�С�fortran��$\frac{x^{2}}{\sin(x)}$�Ȥ���x,y�ǡ��������
implicit real*8(a-h,o-z)
x=0.
do i=1,100
x=real(i)/10.
print*, x,x**2/sin(x)
end do
end
6/21�ޤ�
- Salome-Gmsh-cgx-ccx��ľ���Τ̤���������4ǯ���Ƕ�ͭ����
- ������
web1w.tex, web2w.tex, web4w.tex(�����ե������)�����������ɤ��ơ�
vi���Խ���platex�ǥ���ѥ��롢pxdvi��ɽ���ʤ�TeX�λȤ����˴���Ƥ�����
5/28�ޤ�
������g77�����β���3�ޤǤ�vi�ǥץ������������������ѥ��뤷�Ƽ¹ԤǤ��뤳�Ȥ��ǧ���롣
5/21�ޤ�
������vi�λȤ��������̤�Ǥ���褦�ˤʤä���ǡ�
������g77�����β���2�ޤǤ�vi�ǥץ������������������ѥ��뤷�Ƽ¹ԤǤ��뤳�Ȥ��ǧ���롣
�ߤʤ���δĶ��Ǥ�gfortran�Υ���ѥ���ȼ¹Ԥϡ�
$vi hoge.f90 ����ǥץ������hoge.f90��ͳ�����Ǻ���
$gfortran -o hoge hoge.f90�����ǥ���ѥ���
ls�dz�ǧ����ȡ��п�ɽ����hoge*�Ȥ����¹ԥե����뤬�Ǥ��Ƥ��롣
$./hoge �Ǽ¹�
5/14
ǽ��Ǽ¸�
4/23�ʹߤβ���
4/23�ޤ�
- �����Υ֥饤��ɥ��å���������5ʬ���٤��ܰ¤ˡ�
2011ǯ��
�����ץ��ѥ�
����
15�Ĥο����
��û52.4cm�����Ĺ120.0cm�ޤǤ�ʲ��Τ褦����ʬ(�����1ʬ�Ǹ������Ϥ�)
1 cos(��t)= -0.244964 L= 120
2 cos(��t)= -0.244859 L= 111.666335
3 cos(��t)= -0.244754 L= 104.171583
4 cos(��t)= -0.244649 L= 97.40681
5 cos(��t)= -0.244544 L= 91.280206
6 cos(��t)= -0.24444 L= 85.713953
7 cos(��t)= -0.244335 L= 80.641744
8 cos(��t)= -0.24423 L= 76.006796
9 cos(��t)= -0.244125 L= 71.760255
10 cos(��t)= -0.24402 L= 67.859907
11 cos(��t)= -0.243915 L= 64.269118
12 cos(��t)= -0.24381 L= 60.955975
13 cos(��t)= -0.243705 L= 57.892576
14 cos(��t)= -0.2436 L= 55.054436
15 cos(��t)= -0.243496 L= 52.42
�ϥ��֥�å��ڶ�
������
�νŷ�ñ����
�Ƶ٤ߤβ���
- ���ġ�����(�ޤ��Ϲ��ʤ�)��ñ����(��ʬ�۲ٽ�)�������ǤDzơ�
������(��¤�ϳؤθ���)��3��礦�������줬�Ǥ����顢���ѹ�������ǥ��Ƥߤ롣
- ��ƣ�������ȱ���������Ϥ⤦�ҤȲ�������ʢ�ޤ�پ��Υץ���������Ĥ�����äơ��⡼�ɲ��Ϥ��Ƥߤ롣
- ������ʬ����ˡ��������ˡ�θ�Ƥ����ä����Ȥ�ޤȤ�롣�ޤ��ϻŪ�˻��Ƥ����̿���Ȥäƥ����֥���Х�����������������äƤߤ롣����������ͥ��������Ƥ���С�����ˤĤ��Ƥ�Ÿ˾��
- ����ڹ⸦���������Τ��Ф���ʤ���ˤ��G¬��Υ��ߥ�졼������CalculiX�Ǥ�롣
- ���ġ���λ�Τ�105*105*150���餤���ڤ�Ф�����ǥ���Ф��ơ��������Ȥ����Ϥ��ơ�������뤫�ɤ�����
��ȵ�Ͽ�ʤ�
�Ѹ쥼��
����ץ��ݡ�����
4/18�ˤ�äƤۤ�������
- ��������/����������
- root�桼�����ˤʤäơ����åץ��졼�ɤǤ���
- ���ܸ�ε�ư/��λ(����ƻص�ư�����������Ϥ������ʤ�)
- Wiki��´���������
- ���Υ֥饤��ɥ��å���3ʬ����ǤǤ���褦�ˡ�
- ������UNIX���ޥ����Ф��롣
- ;͵������С�2010ǯ�٤���Ȥ�����˿ʤ�
2010ǯ��
6/10�ޤǤν���
�����������Τǡ���«������ɽ��gnuplot�ǥ���դˤ��ơ�xfig�˼�����ǡ���������������ߡ�
����������TeX�ե�������������ơ����������ʸ�ʤɤ�TeX�����ˤʤ����ơ�
���֤ʤɤ���Ĵ�����롣
6/3�ޤǤν���
web2e.tex�դ�ͤˤ��ơ���wiki�ˤΤ��Ƥ�ɽ��TeX�ǽơ�����äȤ����ͻ���ä��ơ�
��ݡ��ȤˤޤȤ�Ƥߤ롣
5/27�ޤǤν���
ccxkataz.f
�κܲپ���ͳü��4���ߤ�p, 2���Ǥ����äĤ��Ƥ�������(4���߰ʳ���4��)��2p,
4���Ǥ����äĤ��Ƥ�������(���հʳ�������)��4p�Ⱥܲ٤Ǥ���褦�˽������ơ����١������Ѱ̤�dat�ե����뤫���ɤ�롣
;͵�Τ���ͤϡ�����ü����Ω����ʿ����y,z���ꡢ�������о�����x,z���ꡢ����ʳ���z�Τ߸���˽������Ƥߤ�(Ⱦ���Ϥ��������ccxkata.f�ζ�����郎���ͤˤʤ롣
5/20�ޤǤν���
ccxkataz.f��Ȥäơ��һ����¤ζʤ���������������x,y,z����������ʬ����Ѥ��Ƥ��äơ�
$v=\frac{P\ell^{3}}{3EI}$�ǵ�ޤ뤿��ߤȤ����и�����ͻ���
�ߤ�ʤ�Ʊ����Τ�Ƥ⤪�⤷�����ʤ��Τǡ�����������礭���ʤɤϡ��Ƽ���
��ͳ�����ꡣâ����1m*1m�����̤ιݺ�Ȥ�����Ū�ʤΤ��롣
���ͻ����Ȥ��ơ�CalculiX���
�ۤ�Ȥϡ�����դ������Τ�˾�ޤ������ɡ�
����ɽ
�ͤ����и�����ɽ��ƤߤƤ⤤�����⡣
5/13�ޤǤν���
������
������
(�����������¤���)�Υޥ˥奢��ͤˤ��ʤ��顢
- ccx�����ϥǡ�����Ȥ���
��������
beam8p.inp �ʤɤ����������������
- ccx_1.7 beam8p �Ȥ��Ƽ¹�
- beam8p.dat��beam8p.frd�ʤɤν��ϥե����뤬�Ǥ������Ȥ��ǧ����vi�ʤɤ���Ȥ��ɤ��ʤäƤ��뤫���ǧ����
- cgx_1.7 beam8p.frd��cgx�Dz��Ϸ�̤�ɽ���Ǥ��뤫�ɤ�����ǧ��cgx_1.7�Ǥ��ޤ������ʤ��Ȥ��ϡ�cgx_1.6�⤿�ᤷ�Ƥߤ롣
- salome������������(�����������¤��ꡣ����Τߥ��������ġˤ˽���Ǥ�����salome�����餻�Ƥߤ������ϡ�Salome��������Τǡ�
4/23�ޤǤν���
������vi�λȤ��������̤�Ǥ���褦�ˤʤä���ǡ�
������g77�����β���2�ޤǤ�vi�ǥץ������������������ѥ��뤷�Ƽ¹ԤǤ��뤳�Ȥ��ǧ���롣
�ߤʤ���δĶ��Ǥ�g77�Υ���ѥ���ȼ¹Ԥϡ�
$vi hoge.f ����ǥץ������hoge.f�����
��ͳ�����Ǻ����������ϡ�
$g77f -o hoge hoge.f�����ǥ���ѥ���
ls�dz�ǧ����ȡ��п�ɽ����hoge*�Ȥ����¹ԥե����뤬�Ǥ��Ƥ��롣
$./hoge �Ǽ¹�
4/15�ޤǤν���
TeX�ط�
TeX�Τ褯�Ȥ����ޥ�ɤϡ�Anthy�˼�����Ͽ���Ƥ���Τǡ�
����
�ˤ���褦�ˡ���bc�פ�\begin{center}�Ȥ����֤�c�פ�\end{center}�Ȥ��Ф��ޤ���
2009ǯ��
���߽з�
| ���� | ���� | �ĸ� | Ȫ�� | ��� |
| 4��22�� | | | | |
| 5��13�� | | | | |
| 5��20�� | | �� | | |
| 5��27�� | | | | |
| 6��3�� | | | | |
| 6��10�� | | | | |
| 6��17�� | | | | |
| 6��24�� | | | | |
| 7��1�� | | | | |
| 7��8�� | | | | |
| 7��15�� | | | | |
| 7��22�� | | | | |
| 7��29�� | | | | |
�Ƶ٤ߤν���
4�Ͷ���(���ʬô���Ϥä��ꤹ��ޤǤ�)
- ����Ȼ�ΰ�ĥ���Ԥʤ����Ψ�����������Ȥߤʤ����ݥ��������¬�ꤷ�Ƥߤ롣
- ��������������ڹ��ܥ�ɤ��������Ȥ���������¬��ϽŤͤƷפ뤫�Ȥ�������
- ��ǯ�٤���¤��˼�Τ褦�ʥ����䥫�åȱ������ޤ���߱����ΰ��̡���ĥ����äƤߤ롣�����̤ϼФ�ˤ��ơ�
- �¸��Υ���Ȼ���ޤ���߱����ν�����CalculiX������ƿ��Ͳ��Ϥ��Ƥߤ롣
- �����������פβ����Ĥ��������ꤷ�ơ������䥫�åȤλ��ѥץ졼�Ȥ˼���Ū������������¤��CalculiX�ѥǡ�����ץ������ޤ���Blender(obj��������)�Ǻ�äƤߤơ�����ζʤ����Ϥ��äƤߤ롣
�롣
ʬô�β�ǽ���Ȥ��Ƥ�
- �����䥫�åȼ¸����ޤ���߱����¸�������¾���ޤ�湽¤�¸�
- �����䥫�åȼ¸����ޤ���߱����¸��������Ĥ�����ǥ��
���Ĥ���
- ��ǯ��´����������Ʊ�����Τ��ޤ���߱����ο�ʿ�Х���ʬ�η���
- �ǽ�Ū�ˤϡ��ʲ��γƼ��β���ˤĤ��ƤȤ�ޤȤ��Τ�TeX�����ơ�
��������
�֤��Ƥ������ڳز����̻�����������ǤޤȤ�Ƥۤ�����
���Τ���ˤϡ�
LaTeX�δ���Ū�ʻȤ�����
��
gnuplot��Xfig�οޤ�LaTeX�˼�������ˡ�ˤĤ��ƻ�Ժ������ʤ�����������ɬ�פ����롣
´�����ס�´�����Ρ����̻������Ƥʤɤϡ�������ˡ�Ǻ������Ƥ�餤��
pdf��
���롣�Ƶ٤ߤν���ǤϤʤ�����´��ȯɽ��ز�ȯɽ�Υ��饤�ɤϡ�LaTeX�Ǻ�äƤ�OpenOffice?�Ǻ�äƤ�褤��
5/19�ޤǤν���
5/19�ޤǤν���
- g77������
�����¹Ԥ����ʤ������2�ޤǤ�롣;͵�Τ���ͤϲ���3�ޤǡ�
5/27�ޤǤν���
�嵭�β���3���Ǥ����ͤϡ��ʲ��Υץ��������롣
- 2�ѿ�x,y�����
- x,y��Ŭ���ʿ��������Ϥ���
- x��y�����촹����(x=3,y=2)
- �ʾ��x,y�ʳ��ˤ��ѿ���Ȥ鷺�˹Ԥ���
���Τ餻
����10:30������ر��������˹�¤�ϳ������μ��Ȥ�c317�Ǥ�äƤޤ���
���Ƥϡ�3�����ΤҤ��ߥƥ����ϥƥ�Τ����ȯ���ơ�
�¤���ʬ������$-EI\frac{d^{4}v}{dz^{4}}+q(z)=0$��Ƴ���ޤǤ�Ƴ�Ф˽������֤��ޤ���
�����Ϥ��ޤ����Ǥ���������ä���ȡ�
(��¤�ϳشط����ä��̤��䤹���ʤä�)�������ʤȻפ��ޤ���
����5/12(��)�ޤǤν���
- 5/12�˴�ñ�ʼµ����Ԥ���
- vi�����ܸ���Խ���Ԥ����ϡ����ܸ줬���äѤ�����С����ܸ쥳����(EUC)��
��ưȽ�̤ˤۤ��������뤬�����ܸ줬���ʤ���Τ��Խ�������ϡ�
��Ƭ�ˡ֤�������ܸ�פʤɤ����餫�����ܸ��Ƥ����Ȥ褤��
�����ʸ��
�����䥫�åȤ�����������(����Τߥ���������)�˽Ƥ�����
���ߤˤĤ���
- ���ߤϿ���13:00����
- �Ƶ٤���ϥ��ߤϵ٤ߡ�������������Ф���
´������ˤĤ���
- ���ߤؤλ��ä�´������˽ƤϤ���
- �����ʸ�����ɤȤ�´���ץ��ݡ�����μ��Ȼ��֤Ȥ��ƿ������Ƥ����Τ��ʣ���Ƥϥ���Ȥ�����̣
- ´���˴ط��������ߤβ���ʤɤ�Ԥä���Ȼ��֤�ΤϤ�����
�֥饤��ɥ��å�������
- abcdefghijklmnopqrstuvwxyz
- ABCDEFGHIJKLMNOPQRSTUVWXYZ
- aBcDeFgHiJkLmNoPqRsTuVwXyZ
- AbCdEfGhIjKlMnOpQrStUvWxYz?
- 3.1415926535(5��)
- 1.7320508075(5��)
ABCDEFG�ʤɺ����ʸ�����ǤĤȤ��ϱ���ξ��ؤ�
SHFT����������
HIJKLMN�ʤɱ����ʸ�����ǤĤȤ��Ϻ���ξ��ؤ�
SHFT���������롣
����Ū���Ҽ��SHFT��ʸ����������Ĥ�����Ȥ���
���ȤΤʤ��褦�ˡ�Enter������(�����ž������)����ξ��ؤǡ�
�ؤ��Ϥ��¤���Ӥ���ʬ�ϴ��ˤ��äĤ������֤ǻش���ζʤ����Ф��ȼ��β�ž�Τߤ�
��ͳ�٤�Ȥ��������Ӥ�����夲�ʤ��褦�ˤ��롣
�ơ��ط����
��ǽʬΥ���پ�
2008ǯ��
���Τ餻08/10/17
��ñ�ʼ��ʤ顢
ASCIIMathML��
�Ȥäơ�TeX�����ǽ�褦�ˤ��Ƥߤޤ�����
���Ф餯����Ѥ��ޤ���
$\epsilon_{zz}(x,y,z)=\lim_{dz \to 0}\frac{u_{z}(z+dz)-u_{z}(z)}{dz}
=\frac{\partial u_{z}}{\partial z}$
��¤�ϳ�����
��ر��μ��Ȥ����ˤ�14:30-16:00�ˤ��ͽ��Ǥ���
���Ƥϡ�
��¤�ϳ�II������δ��������ˤΤäȤäơ�
��Ϣ³�Τ��ϳءפˤɤΤ褦�ʶ����Ԥäơ�
�ɤΤ褦�ʿ���Ū��Ƴ�Ф�Ԥ���
��¤�ϳؤ��¥�ǥ���¤���ʬ��������
Ƴ����뤫�Ȥ������Ȥ�����Ȥ�ꤿ����
�פ��ޤ���
�Թ�ε����ͤϡ��Ǥ���������ä��Ƥ���������
ʸ���ʤ�
�Ƶ٤ߤν���
����
����Υ��ߤ���ˤ����ˤθ��1������ˤ������Ȼפ��ޤ�����4�ͤ��Թ�˱����Ʒ��Ƥ�������
(���ˤ���ˤ��Բ�ǽ�ǤϤʤ��Ǥ�)��
�ǡ�10��κǽ�Υ��ߤ����˲Ƶ٤ߤν��������ʪ1�����˰������Ƹ�ƣ����Ф�����ǡ�
����(���������Ȥ��Ƥ��ơ������ä��顢�ɤ��ʤä��������ޤ����äƤ��ʤ����Ȥ�ޤ�ơ�
�����ɤ����������ʤΤ�)��ۥ磻�ȥܡ��ɤ�Ȥäƴ�ñ��ȯɽ���Ƥ���������
���̻���
- �ǽ�Ū�ˤϡ��ʲ��γƼ��β���ˤĤ��ƤȤ�ޤȤ��Τ�TeX�����ơ�
��������
�֤��Ƥ������ڳز����̻�����������ǤޤȤ�Ƥۤ�����
���Τ���ˤϡ�
LaTeX�δ���Ū�ʻȤ�����
��
gnuplot��Xfig�οޤ�LaTeX�˼�������ˡ�ˤĤ��ƻ�Ժ������ʤ�����������ɬ�פ����롣
´�����ס�´�����Ρ����̻������Ƥʤɤϡ�������ˡ�Ǻ������Ƥ�餤��
pdf��
���롣�Ƶ٤ߤν���ǤϤʤ�����´��ȯɽ��ز�ȯɽ�Υ��饤�ɤϡ�LaTeX�Ǻ�äƤ�OpenOffice?�Ǻ�äƤ�褤��
- ʸ������������¾�Ǵ�Ϣʸ������Ը������Ĵ�����뤳�ȡ�
- ���������һ����¤�8�������������Ǥβ��Ϥǡ��������������ʬ�䤷���顢
�ƥ��⥷�����¤Τ���ߤ˶��դ����ɤ����ν���⤢�ä���
����
- �����䥫�åȴ�(�����Ϥ���������ݺ�Ǥ⥢��ߤǤ�)�β��Ϥ롣
- PCCP�������ΤȤ��ˤ���daiya.f��ble6ccx.f��Ȥ���ˡ��ƣ���鶵���ʤɤ��Ƥۤ�����
- daiya.f������ʬ��Ͼ��ʤ��Τǡ����������ʬ������䤹��ˡ��(��٤���乩ƣ����Ȱ���?)�ͤ��Ƥۤ�����
- daiya.f�����������ʬ������䤻�뤳�Ȥ�˾�ޤ����������Ԥ�daiya.f�ν���(daiya.obf)��
blender2.40���ɤ߹��������ʬ���٤�������obj�ե�������Ǥ��Ф��Ȥ���������Ǥ�褤��
- Ŭ���ʱ���(�ޤ�����ϥ��̤��餤���礭���Τ�Τ��оݤȤ��Ƥ�褤)���Ф��ơ���ü����ǡ���ͳü¦���鰵�̤�ä��롣
- �˲��⡼�ɤ��ɤ��ʤ뤫�Ϥ狼��ʤ������¶����Ϥ�ԤäƤߤơ��⤷�¶�������¶��ٽŤȺ¶��⡼�ɤ�Ĵ�٤롣
- �¶��⡼�ɤ�cgx������������ˡ�ϡ�tasu.f���ȡ��⤷�����ƺ���cgx���ȡ�"add displacements"�ߤ�����"add mode"��Ǥ�����
�������������
- �Ѳ�������ѥ����Ȥ��Ƥϡ��⤵�����Υ�����Ŀ����������Υ�����Ŀ����Ѥ��ʤ��顢�¶��ٽŤ��ɤ��Ѥ�뤫��Ĵ�٤�
(����оݤϡ��ޤ��ܤΤʤ����֤α���)��
x�����������Υ��������y�����⤵�����Υ��������z�����¶��ٽŤߤ�����3�����ץ��åȤ⤤�������Τ�ʤ���
- ������Ǻ¶����������ˤʤ����ϡ��ɤ���ʬ�α���(�ߡ���������)���������Ϥ�ã���뤫��Ĵ�٤롣
���
- �ޤ���߱���(�����Ϥ���������ݺ�Ǥ⥢��ߤǤ�)�β��Ϥ롣
- PCCP�������ΤȤ��ˤ���tubure.f��ble6ccx.f��Ȥ���ˡ��ƣ���鶵���ʤɤ��Ƥۤ�����
- tubure.f������ʬ��Ͼ��ʤ������ޤ���ߤ��Ӥ����ʤ֤��ʤ��Τǡ����������ʬ����ޤ�����ʿ������䤹��ˡ��(��������乩ƣ����Ȱ���?)�ͤ��Ƥۤ�����
- �ʲ��˽Ҥ٤�褦��1�Ĥ��ޤ���ĺ�����ն�ζ����¶���Ĵ�٤뤳�Ȥ�1�Ĥδؿ����ʤΤǡ��ޤ�����ʿ���2�ʤǤ⤤��������2�ʤ��Ȳٽźܲ�����¦�˱��Ͻ���Ȥ��αƶ����Ф����ʤΤǡ������4��(����ü/\/\��)���餤�Ϥ��ä����������ΤǤϤʤ����Ȼפ���
- tubure.f�����������ʬ��(��2�ܤ��餤�κ٤����Ǹ���Ǥ⤤������)��Ǥ�դ��ʿ���ư������Ǥ��뤳�Ȥ�˾�ޤ����������Ԥ�tubure.f�ν���(daiya.obf)��blender2.40���ɤ߹���ʤɤ��Ƽ�ư������ʬ���٤����������ʿ������䤷��obj�ե�������Ǥ��Ф��Ȥ���������Ǥ�褤(�����դΥΥ��ϥ��Ϲ�ƣ�����ΤäƤ�)��
- �ޤ���ޤ줿�����ʿ���������Ӥ���̤����ʤ��ä��ꤻ���˹��ΤǤ���С��ޤ���߱����Ϲ⤵0�ΤԤä���ξ��֤ˤʤ롣���ξ��֤������֤Ȥ��ơ������ΰ�ü����ꤷ��¾ü�����ĥ�äƤ��äơ��ޤ��ܤ��Ĥ֤줿��ζ����¶��Τ褦�ʸ��ݤ�ѻ����뤿��˺¶����Ϥ��롣�⤷�����ƹ⤵0����β��Ϥ����ޤ������ʤ����ϡ���������Ȥ��Ƥ������٤ι⤵��Ϳ���Ƥ�褤
(���ξ�硢���̤��Ƥ⤭�줤���ޤ����ʤ��ʤ�Τ��ʡ��ޤ����Ϸ����ޤ��ܤγ��٤������Ȥ����ȤԤä���ˤʤ�ʤ����)��
�Ĥޤꡢ�Ԥä���δ������ξ��ϡ��ɤ��ޤǰ���ĥ�äƤ�����פ�(�����¶��������ʤ���)��
�ǽ餫��⤵�Τ����Դ������ξ��ϡ�����˲ä��Ƥɤ��ޤDz�������Ǥ�����פ�(�����¶������ʤ���)�Ȥ������Ȥ�
�ؿ����˲ä�뤫�⡣
- Ŭ���ʱ���(�ޤ�����ϥ��̤��餤���礭���Τ�Τ��оݤȤ��Ƥ�褤)���Ф��ơ���ü����ǡ���ͳü¦�����ĥ��ä��롣
- �˲��⡼�ɤ��ɤ��ʤ뤫�Ϥ狼��ʤ������¶����Ϥ�ԤäƤߤơ��⤷�����¶�������¶��ٽŤȺ¶��⡼�ɤ�Ĵ�٤롣
- �¶��⡼�ɤ�cgx������������ˡ�ϡ�tasu.f���ȡ��⤷�����ƺ���cgx���ȡ�"add displacements"�ߤ�����"add mode"��Ǥ�����
�������������
- �Ѳ�������ѥ����Ȥ��Ƥϡ�������������θĿ�������ξ����������������⤵����Ψ�ʤɤ��Ѥ��ʤ��顢�����¶��ٽŤ��ɤ��Ѥ�뤫��Ĵ�٤�(����оݤϡ��ޤ��ܤΤʤ����֤α���)��
- ������Ƕ����¶����������ˤʤ����ϡ��ɤ���ʬ�α���(�ߡ���������)���������Ϥ�ã���뤫��Ĵ�٤롣
����
����ο����������������(��ư�����Ȥ�)��Ĵ�٤Ƥߤޤ����Ȥ��������Ǥ���ʸ�ˤʤ�ʤ��Τǡ�
������Ū�˽����蹽¤(���ϥ�٥뤬�����������������फ��ʤ륷���빽¤�Ȥ�)����ͭ���������
(���ٺ��ˤ�뿶ư��¶��Ȥ�)�˴ؤ���ơ��ޤ�ʸ�������ʤɤǸ��դ��Ƥ���ɬ�פ�����Ȼפ��ޤ���
�ǡ����ˡ����蹽¤�Τ���ѥ���(�����Ȥ����¹�¤�Ǥ�����Ĺ��ѥ����ߤ����ʤ�ΤȤ���������Ȥ���
���٤Ƥ�����������Ѥ�ʿ�Ѹ��������Ѥ���Ψ�Ȥ���ñ�̻���������β��ٺ��Ȥ�)��
�Ф��뿶ư����(��ͭ��ư��)�Ȥ���Ĵ�٤뤳�Ȥ���ĤΥơ��ޤˤʤ�����Ȥ��ơ�
��ñ�ʿ�����(�ޤ��ϱ��蹽¤)��ǥ�(ñ�ʤ�Ȣ�Ȥ��ĤȤ���ñ��ʥ�ǥ�)���Ф��ơ�
���Υѥ����������ͤ˶��դ��ȸ�ͭ��ư�����������ʤ�Ȥ�����������
(����Ū�����Τ�ʤ�)�θ��Ф����Ȥ��ơ������θ��γ������
�ǥ�ȥ졼�����Ȥ��ơ���������¤�μ�����Ф��Ƥ��Υѥ�����Ĵ�᤹�뤳�Ȥ�
����Ū�ʱ��蹽¤���߷פκݤ˸�ͭ��ư������Ĵ������Τ˺����ȯ��
(����ѥ����������ͤ˶��դ��ȿ�ư�������ɤ��ʤ�)�����ѤǤ���Ȥ��ä�
����Ū�ʹͻ���Ȥ��ä������Ǥ��礦����
- pccp������?�ΤȤ��ˤ���ble6ccx.f��blender2.46��obj�ե�������ɤ߹���褦�˲�¤����Τϡ�
�������ʤ��褦�ʡ�
- ���뤤�ϡ�blender2.46��obj�ե������vi�dz����Ƽ�ư�ǡ�blender2.40��obj�ե���������˽�����
���Ȥ�Ǥ��ʤ��Ϥʤ��Ȼפ��������ֹ椬0�֤���ǤϤʤ�1�֤���Ϥޤ�Ȥ����������Τϡ�ble6ccx.f�������б���������
�������������ɡ�
����
- ���Ĺ�ʡ�¸����
- ��ǯ�ι�ʡ��������Ĥ������ʸ���ɤ�ǡ���ʡ��������Ĥ���������Ф��ƹԤä���Ϣ�β��Ϥ�
�����Υޥĺ���Ф��Ƥ�ԤäƲ�������
�����������ʸ��Τ�(���֤�)�������������ʤ��顢�������ؤ�Ǥ���������
����줿��������ˤ�ȤŤ��ơ�ccx�ǤΥ��ߥ�졼�������äƤۤ���������ɡ������դ��������������̡�
���ߤˤĤ���
- ���ߤϿ���13:00����
- �Ƶ٤���ϥ��ߤϵ٤ߡ�������������Ф���
´������ˤĤ���
- ���ߤؤλ��ä�´������˽ƤϤ���
- �����ʸ�����ɤȤ�´���ץ��ݡ�����μ��Ȼ��֤Ȥ��ƿ������Ƥ����Τ��ʣ���Ƥϥ���Ȥ�����̣
- ´���˴ط��������ߤβ���ʤɤ�Ԥä���Ȼ��֤�ΤϤ�����
�֥饤��ɥ��å�������
- abcdefghijklmnopqrstuvwxyz
- ABCDEFGHIJKLMNOPQRSTUVWXYZ
- aBcDeFgHiJkLmNoPqRsTuVwXyZ
- AbCdEfGhIjKlMnOpQrStUvWxYz?
- 3.1415926535(5��)
- 1.7320508075(5��)
ABCDEFG�ʤɺ����ʸ�����ǤĤȤ��ϱ���ξ��ؤ�
SHFT����������
HIJKLMN�ʤɱ����ʸ�����ǤĤȤ��Ϻ���ξ��ؤ�
SHFT���������롣
����Ū���Ҽ��SHFT��ʸ����������Ĥ�����Ȥ���
���ȤΤʤ��褦�ˡ�
| �� | �� | �� | �� | �� |
| ���� | | | | �� | |
| ��� | �� | �� | | �� | �� |
2007ǯ��
ʸ������
�����ץ��ѥ�
�����ޤǤλŻ�
- ����Խ���ᡢ��¤�������ɽ��ޥ��å��ǽ��ɤ�Ž�������ɡ�
�ޥ��å����ɤ˼̤�Ⱥ���Τ���¤����˿�ʹ�椫�ʤ�Ž�롣
- �����ˤҤ���դ���
- �ݥ�������Ž��(�¸����Υɥ����ս�ˤϡ֣����Ǥ��פ�Ž��)
- ���10�����¤٤�����Ѱդ���(ï�ζ���ʬ����褦�ˤ���)
- ��ǯ�Υݥ�������Ž��(������ά��)
- �ɥ�¦�˥ơ��֥��2�Ĥʤ�١��嶶�������������������������Ĥ궶����Ÿ��)
- ����Linux�ѥ������ɤä����֤��ƥǥ����ȥåפ�spa���������å�����totem-xine�ǵ�ǯ��
��¤��˼��ư����ԡ��Ⱥ������Ƥ���
�����η�
- �̿���(����ξ��֡��ܲ��桢�˲�ľ��ξ��֤�)
- �ӥǥ���(�������ͻҤ�)
- ��Ͽ��(���š������ٽš������ٽ�/���Ťʤɤη�̤���¤���Wiki�˵�Ͽ)
- ���ڤ���(�������ǤϤ��줫���˲��¸���Ϥ�ޤ��Τǡ�����)
����Υ��ߤ�����Ĵ��
- ����13:00
- ��ƣ�����ܤ���
- ����?����ʪ���¸��äƲ�������?
- ����10:00-12:00�������ʪ��
- ����8:50-10:20��¤��˼�½�(���뤤�ϡ��虜�ȥ��ߤȤ��֤��Ƥ⤤�����⡣�ܲٻ�ΤȤ��Ȥ�)
- ����14:30-16:00��������ε�ˡ
�Ƶ٤ߤν���
Calculix
- ����:�¸���Ʊ�����̤�PLASTIC������ƲƤߤ�
- ��ʡ:���������μ�����
- ����:�ߴɤ�ɽ�̤˱�ä�8�������������Ǥ��ʤǥ�ǥ벽�Ǥ��뤫
- ����:�¶�����Ѱ��̤�����ɸ�����ơ��ѷ��ޤ�cgx�������뤫
Xfig+LaTeX
- ��ƣ�μ������β���(�㤨�и��ե�����̾:hoge.png)��Xfig������ľ����
�����Ԥ�̾���˱�����(����:oo, ��ʡ:ta, ����:ho, ����:ya)hoge07oo.fig�ߤ�����
̾�����դ�����¸��
- LaTeX eepic��Export���ơ�hoge07oo.tex�Ȥ�����¸��
- Ŭ����tex�ե�������ɤ߹���ǡ�ʸ���������
- ��¤�ϳإƥ����ȤΥڡ���
�˼ռ��Ȥ��Ʋ�����ԤΤߤʤ����̾����ܤ��뤬��
fig�ե������tex�ե�����ϸ�������ï�Ǥ⼫ͳ�˻ȤäƤ������Ȥˤ�����
(�Τǡ����ξ��ˤɤ����Ƥ⽾�������ʤ����ϡ����ν���Ϥ��ʤ��Ƥ⤤��)��
���ѥ��åƥ����ζ�
- 1��1��(10/20�Υ����ץ��ѥ������и�����)
- �����ʤμ��š�200g�ʲ�
- ���ѥ�60cm�ʾ�
- �����ٽš����ŤǶ���
- ���ѥ��åƥ�������ޤ����äƤ�VALLE DEL SOLE(4kg��400�ߤ��餤��)
- �ִ�����ޡ�100�ߥ���åפΥĥ���� �ץ�����3g
- ��������˺ܲ��Ѥβٺ��Ҥ�(��47mm)���̤����֤��ߤ���
- �ܲ�����������Ǥ���в����Ǥ�����Ǥ��ʤ�
����䥢�ѡ��ȤǶ�����ͤϡ����夦�֤�˴������ʤ����Ȥ��Ʋ������� ������ե��ʤ��������㤽���Ǥ������ĥ����ϥ����Υ�����졼�Ȱʳ�����ʬ���ɤ����ٴޤޤ�Ƥ��뤫�ʤ������ʤΤǡ�
����6/4�ޤ�
ccxkataz.f��
���һ����¤Τ���ߤ�PL^{3}/(3EI)����Ӥ��롣
����5/28�ޤ�
���̤β���
| �� | �� | �� | �� | �� |
| ���� | �� | �� | �� | | |
| ��� | ��1���� | �� | �� | 14:20���ޤ� | �� |
´���ơ���
- ´���ơ��ް�(4����)
- ��������������μ¸��Ȳ���(�ں�ȹݺ�Υ������αƶ�)(�����ڤ���ƣ)
- �¸��Ϻ���1�ͤ�ô�����Ƥۤ������¸��ˤ�ô���ʳ���ˤʸ¤������ǽ��˹Ԥ������Ĥ���μ¸���Ŭ�� ��������(����)
- ���������������¤Τ������������������������Τ������������ʬ������ͤȡ�ͭ������ˡ����εջ��ͤȤ����(sounyuuk.f)(��ʡ)
- �ݴɤ������¶�(�ݤ��¶�):���ܹݹ�¤����饤�֥�Vol10,No39: �ݤ��¶��ˤ����������ȼ¸����¤�ЪΥ�Τ褦�������CalculiX�Dz���(����)
- ���ͤ���¶��ο��Ͳ���: ��û���ȼ¸��ͤ�Ω������FEM���ϲ��������FEM��Υ��뷹������
���ޤ��¸�������Ω������FEM�ο������η��������Ƥ��뤫��ʤΤ����¤ϸ����Τ����ǤϤʤ��Τ���CalculiX��
Ω�����Ǥ������¶����ϤǤϤʤ������������Ϳ�����ѷ����ɤ������ʤ���¶����Ϥ������̤��Ѥ�äƤ��뤫�ɤ���
(��ƣ)(����)
- ͽ����
- ���å��夵��FEM��ǥ벽���褦�Ȥ��Ƥ���?�������Ȥ����ݶ��ѻ�����ˤ���褦�ʿ�����ʣ�繽¤��ͭ�����ǥ�ǥ벽
- ���蹽¤�ͥ�:����ܥ��դ������κ¶����ϡ��ȶ�ʻ�ΤȤ��ơ�
����ܥ��դ������̤��ڤ�Ф��ƺ��������ǡ����̻��Ԥ��������CalculiX�ǥ��ߥ�졼����Ƥɤ줯�餤�礦���Ȥ���
- �ݹ�¤(�������Ȥ�)��ʣ�繽¤(���ӤȤ�)�ο��Ͳ���(��ƣ)
- ����¾�Υͥ���ʸ�������Ǹ���
- ���ϥܥ�Ȱ�ĥ�ܹ�ΤƤ�ȿ��
- ���̻����ˤĤ���
CalculiX����(�Ѹ쥼��)
- Calculix��1��1�㤺�ķ����Ƽ�������(�Ѹ쥼��?4��)
- CLOAD��DLOAD����Ӥ�����ʬ�ۺܲ٤�ư���Ǥ��뤫�ɤ�����ǧ(�¸�ô���Ԥ���������������ô����)
- ����������(�ں�)������������(��)�����Ǥ����Ȥ��ˡ������������Ǥ���������Ǥ�Ϳ���ʤ��Ȳʤ����ɤ�����ǧ(ELASTIC�¸�ô���Ԥ���������������ô����)
- �������ΰ��ֲ��˼�����Ƥ���褦�ˡ��ٽ�������Ѱ���������ؤ��ʤ����¶������ɤ��뤫�ɤ�����ǧ���Ȥ�������CalculiX¦����ưŪ�˲ٽ�������Ѱ���������ؤ��Ƥ����Τ�(�¶�ô����)
- ������������礵���ʤ������ʷ�ϩ�Ǻ¶�������פ����硢�����¶����Ϥθ�ͭ�٥��ȥ�Ȥ��ƺ¶��⡼�ɤ����Ф���ȡ�����������������ѤǤ���Τ������ʤΤ����������¶�����(��ƣ����ä�)����¶��⡼�ɤ����Ф��뤫�ɤ�����ǧ
(BUCKLE�¶�ô����)
- �ٽš��Ѱ���������ؤ����ꡢ���椫�����������줿�ꤷ������硢��Ĥη�����λ���������ΤĤꤢ�����֤Υǡ�������Ϥ��Ƥ����ơ����η��ν�����֤����η��κǽ����֤ΤȤ����������Ԥ���ˡ��ɬ�פˤʤ뤫���Τ�ʤ��Τ�(*)�����줬�Ǥ��뤫�ɤ�����ǧ(�¶�ô����)
- ����¾�β���
- cgx��ץ�ץ����å����Ȥ����������ߤ����ʤ��ʣ����ʣ�繽¤�Υ�ǥ벽���Ǥ��������ɤ������ǧ(������ô����)
- CalculiX�Ǥϥߡ���������(��������)�����������Ҥ��ߴط���Ϳ������������ǥ���ǥ벽���뤬��
�ޥ˥奢��Ǹ����ֺǽ�����פˡ֤����ǹ������ϡפ�Ϳ����Ф����Ȥ������ȤʤΤ��ɤ�����ǧ��
���Ͳ��ϥ��ߤ�������ǧ(�ⶶ�ɤ�Ĵ��)�����ʬô
����(ͽ��)
| 5/25 | unix���ޥ�ɡ�vi(��ƣ��) |
| 6/1 | vi(��ƣ��) |
| 6/8 | Fortran(��ƣ��) |
| 6/15 | �� |
| 6/22 | �� |
| 6/29 | c����(�带) |
| 7/6 | �� |
| 7/13 | �� |
| 7/20 | �� |
| 7/27 | LaTeX(��ƣ��) |
| 8/3 | �� |
��ƣ��ô��
| �� |
| vi | |
| unix | |
| Fortran | |
| LaTeX | |
�ʲ���2006ǯ�٤�����
�����ץ��ѥ�
- �嶶:��ë
- �ȥ饹:��ƣ
- �Ĥ궶:���
- ��ޤ䥸�塼��
- �����åȥƥ��å���
- Ǵ��
- �ڡ��ѡ�����ե�
- �֥ꥳ��mpg
���Τ餻
06/6/9�ʸ�ƣ)
vi���ޤ��Ȥ��Ƥʤ��ͤ⤤��褦�ʤΤǡ�
vi�λȤ���
���ɲä��Ƥ����ޤ�����
2006ǯ�٤�ͽ��
Ϣ������(��ƣ)
- ´������ˡ֥��ߡפȤ��ֱѸ�ʸ���פȽƤϥ���(������´���κ�Ȼ��֤ˤ�����ʤ�)��
- ��Wiki�ġ���λȤ����פȤ��ʤ餤�����ɡ�
- Ω��Ԥϱ����Ǥ��(����ɬ�ܻ������ȡ�
- 5/2�Υ��ߤϵ٤ߡ��٤���˾����Ǥ�CalculiX��������ʤ�Ƥ������ȡ�
- �����5/8(��)14:00���顣
���Ͳ��ϥ���
| 5/24 | Unix; vi(��ƣ��) |
| 5/31 | vi(��ƣ��) |
| 6/7 | C |
| 6/14 | C |
| 6/21 | C |
| 6/28 | C |
| 7/5 | C |
| 7/12 | C |
| 7/19 | Fortran(��ƣ��) |
| 7/26 | Fortran(��ƣ��) |
| 8/2 | Fortran(��ƣ��) |
´���ơ���˾(�ޤ�̤������ɡ��������ĥ�����ͤ�ͥ��?)
- ���ġ��¸�
- �̡���
- ��ë���ʴ�
- ��ƣ��
- CalculiX��Ω�����Ǥ��¤β��ͤ���¶���Ƥߤ�
- ���줬�Ǥ���ʤ顢�ͤ������������������Vlasov��ƥ��⥷���β��ϲ�������Ǥο��Ͳ���Ƥ�������
- �ں�β��ͤ���¶��μ¸��ͤȺ�Ĺ��Ȥδط��������ͤȵդˤʤ�����
- �����
- tyokum<mage.d��5���ܲٻ�Ǥ�äƤߤ롣
- �������¤κ¶�(�ե����ȥ�����������Calculix��Ω�����Ǥ����)
- ��Ĺ��Ⱥ¶��ٽŤδط����¸��ȿ��Ͳ�ǰ��פ��ʤ�
- �����������������������ʤäƤ����Ȳ��ϲ�ȿ��Ͳ��פ��ʤ�
- �ե����ȥ���Ω������(���������ѥ��ȥ�å��б��ˤ���)�Ǥ����ǥ��å���
- �ե����ȥ���Ω������(�˹���Ƚ��������)���������¤�����������(��CalculiX�����)
4/25��Ϣ������
- CalculiX�ޥ˥奢��μ�ʬ��ô���ս���������Wiki��Ž��Ĥ��Ƥ�����
4/18�ν���(�����äȽ���)
������abcdefghijklmnopqrstrvwxyzABCDEFGHIJKLMNOPQRSTRVWXYZ0123456789
��10���Ǥ����ࡣ��ʸ�����ǤĻ��ϡ�ABCDEFG�Τ褦�˺����ʸ���������Ǥľ��ϱ���ξ��ؤ�
���եȥ���������HIJKLMNOP�Τ褦�˱����ʸ���������Ǥľ��Ϻ���ξ��ؤǥ��եȥ��������롣
�Ѹ쥼��
��ǯ�ϡ����20�ڡ������٤��ܰ¤ߤ����ʤ�ǡ�
CalculiX�Υޥ˥奢��ԡ�����20�ڡ�������ʬô���ޤ�����
CalculiX�Υޥ˥奢������������Ѥ�Wiki�ڡ�����ѥ�������¤Ĥ��ǡ�
�������Ѱդ��ޤ�����
�ѥ���ɤϥ��Ǥ��Τ餻���ޤ���
���Ͳ��ϥ���
�带�ȹ�Ʊ�ο��Ͳ��ϥ��ߤϡ�5/24�����轵��������12:50-14:20�ˤʤ�ͽ��Ǥ���
��ƣ�ɤ�ô���ϡ��ǽ��2�餤�ǡ�UNIX���ޥ�ɡ�vi�λȤ�����
�ⶶ�ɤ�C¾�Τ��Ȥˡ��ե����ȥ��3�餤��TeX4�餤
�ʲ���2005ǯ�٤�����
�Ƶ٤ߤν�������
- �ģ֣Ĥ�����ʬ�Τ�����ơ��ݥ��Ȥ�����Ƥ����ޤ�����
���Τ餻
- 9/21(��)�����ѥ������ǡ�
- ���ʤ��Ȼפ����ɡ������ޡ��Ȥ���֤�����ؤ���ʤ��褦��
- 9/12�ν��˻�Ĵ���˹Ԥ��ʤ�����
- 9/20�����Ϣ�٤ϸ�ƣ���ߵ٤�
�����ץ��ѥ�����
- �����ץ��ѥ���(10/8��)
- ����Ȼ�η嶶��Ĥ���
- ���ѥ��åƥ����Ĥ궶�ν���
- ���ѥ��åƥ����ȥ饹��⤦�춶
- ���ڥ������ν���
- �ݥ���������
- �ץ쥼������
- ��ǯ����¤��˼�κܲٻDVD��mpeg��
�Ƶ٤ߤν���
- ��¤�¸�
��Ԥ���LaTeX,Xfig,gnuplot�ǥ�ݡ��Ȥ�������롣
- gnuplot�������������ˡ���ط��������Ϥ���ʤ������Τ�ʤ��Τǡ�
������
kaiki.f
��Ȥä���ط�������Ƥߤޤ��礦��
- CalculiX�����Ϥ����ȿʤ�Ƥ������ȡ�
´���ơ���
- ���ڡ���ƣ�����������Ϸ�
- �����ϼ¸���
- ���ڤϥե����ȥ��
- ��ƣ��CalculiX
- ƣ������
- ���Ӥ��ʴ�
���ͻ���
����6/21
�⤷���ʤ�;͵������С�13:30����C319��(�ػһ�����)�������������ֵ̹���
����6/15
- LaTeX³����
- web3e.tex��hyperref��pdf�����ʤ��ȥ��ͭ���ˤʤ�ʤ���
- AdobeReader?��pdf���������ϡ��֥��ץꥱ�������ע��֥��ե����ע�AdobeReader?
����6/8
����6/1
����5/25
- xfig��hoge.eps���������ץ��åȤ������������롣
- gftp�Ƿ������С��˥ե�����åץ����ɤ����ꡢ�����С�����ե���������������ɤ��롣
����5/18
- �轵������������������Ŭ���������˽��Ͻ�����
- ����줿y=f(x)��x,y�ǡ�����gnuplot�����褷��eps��������¸��
- $ ggv hoge.eps �Ǻ������줿�����ե�������ǧ��
- xfig��hoge.eps���������ץ��åȤ������������롣
����5/11
- g77�ǹ����ʴؿ�y=f(x)�������ץ���������������¹ԡ�
- �ޤ��ϡ�x���ܡ������Ϥ���y����̽��Ϥ���ץ������
(rei1.f��
����������ɤ���vi���Խ�)
- ���ˡ�x��x�����Ѳ��������Ȥ���x,y��ǡ������Ϥ���ץ������
(rei2.f��
����������ɤ���vi���Խ�)
����4/27
- �ޤ����֥饤��ɥ��å��δ��ܡ��ۡ���ݥ������γ�ǧ��
�ѥ�����Ǥ������κ�Ȥ�Ϥ������
abcdefghijklmnopqrstrvwxyz
ABCDEFGHIJKLMNOPQRSTUVWXYZ
01234567890��3���Ǥ����ࡣSHFT�����ϡ�ʸ�����ǤäƤ륭���Ȥ�ȿ�Фμ�ξ��ؤǡ�
- �ۡ���ݥ�������Ф����Ȥ�����vi�δ�����
vi��(��ȸ�Ψ���ò�����)���ϥ֥饤��ɥ��å����Ǥ��Ƥ뤳�Ȥ�����ʤΤǡ��֥饤��ɥ��å����Ǥ��Ƥʤ���
�Ҥ��������ؤǻȤ��ˤ����ʤäƤ��ޤ���
- �ե��������ʸ���������������¸��λ�Ǥ��롣
- hjkl�Υ�����Ȥ��ʤ�����ۡ���ݥ��������֤����ޤޤǥ���������岼�˰�ư�Ǥ��롣
- ʸ���κ�����ִ����Ԥκ��������������
- ����
����4/20
- FD�ǥǥ��쥯�ȥ����ꤷ�ơ��ե�����Υ��ԡ����ư���Ǥ��롣
- MO�ɥ饤�֡�DVD�ɥ饤�֡��ե�å������ʤɤ���³����FD�ǥե�����ԡ��������
�ޥ���Ȳ�����Ƽ�곰����
- �������С�����³����cgx -b dummy.fbd��cgx��ư����CalculiX�Υޥ˥奢�����
����4/13
- ���ޥ�ɥ饤��ǥǥ��쥯�ȥ�β��γ��ؤ��γ��ؤ˰�ư�Ǥ���
- �ǥ��쥯�ȥ�κ����Ⱥ�����Ǥ���
- �ե�����Υ��ԡ�����ư��������Ǥ���
- vi��ư���ƥƥ����ȥե��������Ȥƽ�λ�Ǥ���
- (�ɲ�)��������ˡ�ǥƥ����ȥե������EUC�����ɤ���¸��ľ����more����Ȥ�뤳�Ȥ��ǧ
��4/13
�ƥ����ȥ��ǥ�����(gedit)�ǡ���¸�פ����֤ȡ���¸�ǥ��쥯�ȥ�ȥե�����̾�����
���̤��ФƤ��ޤ����������ˡ�ʸ�������ɡפ�����Ȥ���������Ȼפ��ޤ���
�ǥե������(���⤷�ʤ�����)�Ǥϡ�������Unicode(UTF-8)�ˤʤäƤ���Ȼפ��ޤ�����
���Τޤ���¸����ȡ����ޥ�ɥ饤���more�Ǹ��褦���Ƥ�ʸ���������Ƹ���ޤ���
EUC-jp��������¸���Ʋ���������������С����ޥ�ɥ饤���more �ե�����̾��
��Ȥ������Ȼפ��ޤ���
����4/13
�����ͽ��ʤ�
- TeX�Ǵ�ñ��ʸ�Ϥ�Ƥߤ롣web1e.tex-web4e.tex
- y=f(x)��x,y�ǡ�����gnuplot�����褷�������xfig�˼������������ä����塢
eepic���Ϥ���TeX�˼����ࡣ�ǡ���Ĵ����
