注意:
このページの数式は、
MathJaxを使って書いてます。
数式部分がおかしい場合は、更新ボタンをクリックすると
改善するかも知れません。
太文字のギリシャ文字($\mathbf{\sigma}$など)が、
太文字になっていない($\sigma$)かもしれません。
印刷版で確認して下さい。
その他、おかしい記述があると思ったら、
メールなどで指摘して下さい。
土木の構造物は、橋とか($x,y,z$の3つの軸のうち)1つの軸方向に
細長い棒状のものが多い。
細長い棒が細長い軸の方向(このテキストでは$z$方向)に
圧縮や引張の力を受ける場合は、
(圧縮を受けた際の座屈などを考えなくていいなら)
1次元のバネの伸び縮みでモデル化できるかも知れないが、
橋みたいな構造物は、細長い棒が水平に横たわっていて、
車の重さとか自重とかが鉛直方向に作用するから、
細長い棒が曲げられるような変形をする。
このような変形を表現するには、1次元のバネのフックの法則では
対処できない。
現時点で我々が使える道具としての知識は、
である。
例えば細長い棒が任意の外力を受けて変形したとき、
その任意点の変位を求めることを1つの目的としてみよう。
外力と内力(断面力)の関係は、
力のつりあい
で関係づけられそうだ。
断面の応力を断面で積分して合計すれば、断面力と応力を関係づけられそうだ。
任意点の応力とひずみは、
応力-ひずみ関係で関係づけられる。
任意点のひずみと変位は
ひずみ-変位関係で関係づけられる。
ということは、現時点で我々が持っている道具を使って、
細長い棒が任意の外力を受けて変形したときの外力と任意点の変位の関係を、
ある条件下で求められそうだ。
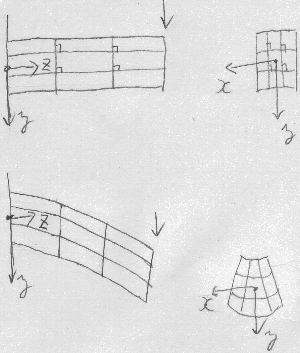 割と太短い棒の場合、図のように棒の側面に直角な枡目を描いておいて
曲げてやると、曲げを受ける平面内でせん断変形が生じて枡目の角は直角では
なくなるだろう。また棒の断面についても、
例えば引っ張られる上辺は軸方向に伸びたぶん幅方向には縮んだり、
圧縮される下辺は軸方向に縮んだぶん幅方向には膨れたりといった変形も
生じるかも知れない。
これらの変形を考慮すると式の導出がなかなか繁雑になってしまうので
(もちろん、それらを考慮すべき場合は、
考慮して繁雑な式を導出すべきだろうが)、
ここではまず簡単な問題として、上記の変形が無視できるような
「非常に細長い棒が、ちょっとだけ曲がる」
場合に限定して考えたい。
という訳で次の2つの仮定を設けることにする。
なお、
このテキストの方針で
梁の細長い軸に沿って$z$軸を取り、下にたわむ方向に$y$軸を取る。
割と太短い棒の場合、図のように棒の側面に直角な枡目を描いておいて
曲げてやると、曲げを受ける平面内でせん断変形が生じて枡目の角は直角では
なくなるだろう。また棒の断面についても、
例えば引っ張られる上辺は軸方向に伸びたぶん幅方向には縮んだり、
圧縮される下辺は軸方向に縮んだぶん幅方向には膨れたりといった変形も
生じるかも知れない。
これらの変形を考慮すると式の導出がなかなか繁雑になってしまうので
(もちろん、それらを考慮すべき場合は、
考慮して繁雑な式を導出すべきだろうが)、
ここではまず簡単な問題として、上記の変形が無視できるような
「非常に細長い棒が、ちょっとだけ曲がる」
場合に限定して考えたい。
という訳で次の2つの仮定を設けることにする。
なお、
このテキストの方針で
梁の細長い軸に沿って$z$軸を取り、下にたわむ方向に$y$軸を取る。
-
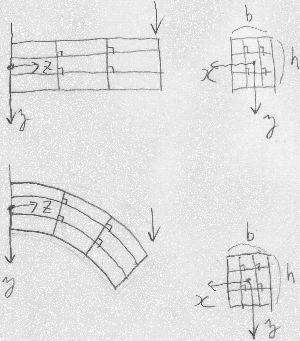
ベルヌーイ・オイラーの仮定
:
図のように棒の側面に描き込んだ直角な枡目は、
棒が曲がった後も直角を保つ。
つまり曲げを受ける平面内のせん断変形は生じない。
ひずみ成分で表すなら、
$\varepsilon_{yz}=0$ ($yz$面内のせん断変形がない)
$\varepsilon_{zx}=0$ ($zx$面内のせん断変形がない)
-
断面形不変の仮定:
棒の断面は、伸び縮み変形もせん断変形もしない。
つまり、棒が曲がった後も断面は変形しない。
ひずみ成分で表すなら、
$\varepsilon_{x x}=\varepsilon_{yy}=0$ ($x,y$方向の
伸び縮み変形がない)
$\varepsilon_{xy}=0$ ($xy$面内のせん断変形がない)
これらの仮定を満たす棒のことをベルヌーイ・オイラー梁
(Bernoulli-Euler梁)とか初等梁と言う。
このテキストで特に注意書きなしで「梁」と書く場合は
初等梁のことを指す。
ちなみに、
ティモシェンコ梁(Timoshenko梁)は、
曲げを受ける平面内のせん断変形を考慮した梁である。
3次元の問題は難しいので、まずは
初等梁が2次元($yz$)平面内で
外力を受け、その平面内で変形する問題を考えたい。
初等梁
の図心を連ねた軸に
沿って$z$軸を取り、梁が下にたわむ方向に$y$軸を取る。
初等梁は、
せん断ひずみ成分や断面の伸びひずみ成分がなく、
ゼロでない唯一のひずみ成分は
$z$軸方向の伸びひずみ$\varepsilon_{zz}$である。
我々は、任意点のひずみと変位の関係を
知っているが、梁の問題では主に図心の変位が分かることが重要なので
(というか任意点の変位は図心の変位と幾何学的に関係づけられるので)、
問題を簡単にするため、
任意点$(x,y,z)$の軸方向伸びひずみ$\varepsilon_{zz}(x,y,z)$を、
以下に定義する図心$(0,0,z)$の変位と関係づけることを試みる。
$v(z)=u_{y}(0,0,z)$ (図心の$y$方向変位: たわみ)
$w(z)=u_{z}(0,0,z)$ (図心の$z$方向変位: 軸方向変位)
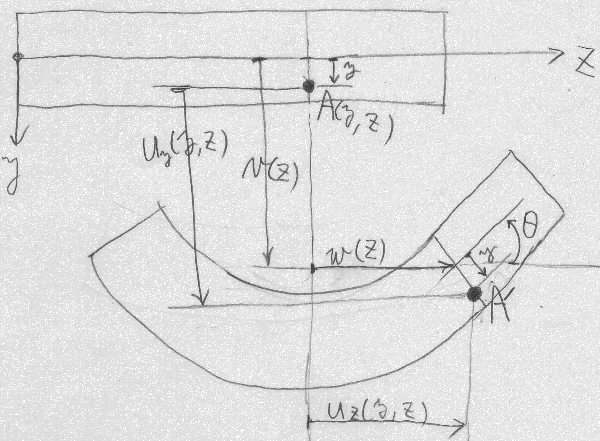 図のように初期状態で梁の
ある断面にある任意点$A$が、梁が外力を受けて変形した後、
$A'$に移動したとするとき、
点$A$の変位ベクトル成分は、
図の幾何学的な関係から次式で表される。
図のように初期状態で梁の
ある断面にある任意点$A$が、梁が外力を受けて変形した後、
$A'$に移動したとするとき、
点$A$の変位ベクトル成分は、
図の幾何学的な関係から次式で表される。
$u_{y}(y,z)=v(z)+y\cos\theta(z)-y$
$u_{z}(y,z)=w(z)+y\sin\theta(z)$
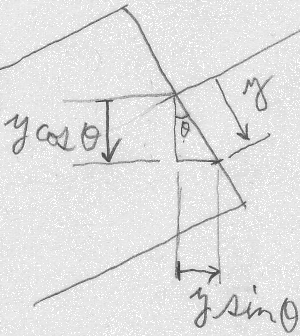 上式の$\theta(z)$は、
初期状態では水平だった(座標$z$での)図心軸
(初等梁では断面の法線と一致)が、
変形後に$x$軸の右ねじまわり(図を見ている人にとっては左回りに)
何ラジアン回転したかを示している。
ここでは、
ベルヌーイ・オイラーの仮定
が成り立つような
$\theta(z)$が1に比べて非常に小さい問題を考えているので、
$\sin\theta(z)\cong \theta(z)$, $\cos\theta(z)\cong 1$と
見なすと、
点$A$の変位成分
は、
上式の$\theta(z)$は、
初期状態では水平だった(座標$z$での)図心軸
(初等梁では断面の法線と一致)が、
変形後に$x$軸の右ねじまわり(図を見ている人にとっては左回りに)
何ラジアン回転したかを示している。
ここでは、
ベルヌーイ・オイラーの仮定
が成り立つような
$\theta(z)$が1に比べて非常に小さい問題を考えているので、
$\sin\theta(z)\cong \theta(z)$, $\cos\theta(z)\cong 1$と
見なすと、
点$A$の変位成分
は、
$u_{y}(y,z)\cong v(z)$
$u_{z}(y,z)\cong w(z)+y\theta(z)$
と書ける。
さてせん断ひずみの定義は、
$\varepsilon_{yz}=\frac{1}{2}
(\frac{\partial u_{y}}{\partial z}
+
\frac{\partial u_{z}}{\partial y})
$
で与えられるが、この式に
ベルヌーイ・オイラーの仮定
$\varepsilon_{yz}=0$と
点$A$の変位成分
$u_{y}(y,z), u_{z}(y,z)$
とを代入してみる。
すると、
$0=\frac{1}{2}(\frac{d v(z)}{dz} + \theta(z) )=0$
つまり、
$\theta(z)=-\frac{d v(z)}{dz}$
となる。
なお、微分記号を偏微分から常微分に書き換えたのは、
$v(z)$は、$z$だけの関数として扱っているからである。
つまり、図心軸の回転量は、(初等梁の場合)
たわみの微分(にマイナスをつけたもの)と
等しくなるが、このたわみの1回微分$+\frac{d v(z)}{dz}$を
たわみ角と呼ぶ。
梁軸方向に$z$(右正)、たわみ方向に$y$(下正)を取る
このテキストの座標では
$\theta$は、
$x$軸右ねじまわりの回転角で、$\frac{d v(z)}{dz}$とは符号が逆になる。
座標の取り方によっては、$\frac{d v(z)}{dz}$の正の向きがそのまま座標軸の
右ねじ回転と一致するように定義されている文献もある。
いずれにせよ($\frac{d v(z)}{dz}$が座標軸の右ねじ回転に一致するかしないかに
かかわらず)
$\frac{d v(z)}{dz}$のことをたわみ角と言う文献もあれば、
$-\frac{d v(z)}{dz}$のことをたわみ角と言う文献もあるので注意が必要である。
この
$\theta(z)=-\frac{d v(z)}{dz}$
の式を点$A$の変位成分
$u_{y}(y,z), u_{z}(y,z)$
に代入すると、以下のように
図心変位
(たわみ$v(z)$と軸方向変位$w(z)$)の関数として書ける。
$u_{y}(y,z)= v(z)$
$u_{z}(y,z)= w(z)-y\frac{d v(z)}{dz}$
さて、
初等梁
でゼロでない
唯一のひずみは$\varepsilon_{zz}$であるが、
任意点$(y,z)$における$\varepsilon_{zz}$は、
伸びひずみの定義から、
$\varepsilon_{zz}(y,z)=\frac{\partial u_{z}}{\partial z}$
であるから、この式に$u_{z}(y,z)$を代入してみる。すると、
$\varepsilon_{zz}(y,z)=\frac{d w(z)}{dz}-y\frac{d^{2}v(z)}{dz^{2}}$
となる。
なお、微分記号を偏微分から常微分に書き換えたのは、
$w(z)$や$v(z)$は、$z$だけの関数として扱っているからである。
今、見やすくするために微分記号を$'$で省略して
$\varepsilon_{zz}(y,z)=w'(z)-yv''(z)$
と書いて、ある断面に着目して例えば$z=z_{A}$を代入してみると、
$\varepsilon_{zz}(y)=w'(z_{A})-yv''(z_{A})$
となる。
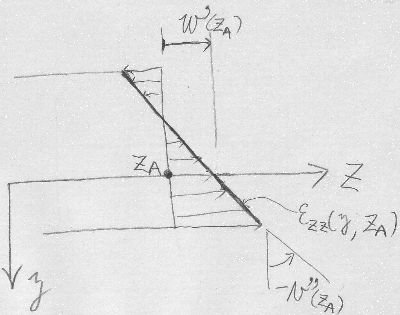 $w'(z_{A})$や$v''(z_{A})$は定数であるから、
$\varepsilon_{zz}$は$y$と線形関係にあり、
$-v''(z_{A})$がその傾き、
$w'(z_{A})$が$z$軸の切片を表している。
つまり、
初等梁
では、軸方向ひずみ$\varepsilon_{zz}$だけが存在し、
任意の断面の軸方向ひずみは、梁の桁高(けただか)$y$方向に対して線形分布
していることが分かる。
これをひずみの三角形分布と呼ぶ。
$w'(z_{A})$や$v''(z_{A})$は定数であるから、
$\varepsilon_{zz}$は$y$と線形関係にあり、
$-v''(z_{A})$がその傾き、
$w'(z_{A})$が$z$軸の切片を表している。
つまり、
初等梁
では、軸方向ひずみ$\varepsilon_{zz}$だけが存在し、
任意の断面の軸方向ひずみは、梁の桁高(けただか)$y$方向に対して線形分布
していることが分かる。
これをひずみの三角形分布と呼ぶ。
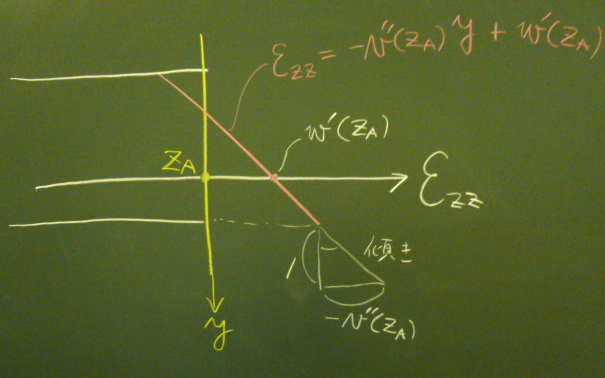 上の図のように、梁の断面上にひずみ(や次回やる応力など)の分布を
重ねて描くということはよくやられるが、
慣れないとちょっとわかりにくいかもしれないので、補足する。
図の断面$z=z_{A}$上に$y$軸を持ってきて、
$z$軸を$\varepsilon_{zz}$としてグラフを描いているということである。
上の図のように、梁の断面上にひずみ(や次回やる応力など)の分布を
重ねて描くということはよくやられるが、
慣れないとちょっとわかりにくいかもしれないので、補足する。
図の断面$z=z_{A}$上に$y$軸を持ってきて、
$z$軸を$\varepsilon_{zz}$としてグラフを描いているということである。
メモ:
 割と太短い棒の場合、図のように棒の側面に直角な枡目を描いておいて
曲げてやると、曲げを受ける平面内でせん断変形が生じて枡目の角は直角では
なくなるだろう。また棒の断面についても、
例えば引っ張られる上辺は軸方向に伸びたぶん幅方向には縮んだり、
圧縮される下辺は軸方向に縮んだぶん幅方向には膨れたりといった変形も
生じるかも知れない。
これらの変形を考慮すると式の導出がなかなか繁雑になってしまうので
(もちろん、それらを考慮すべき場合は、
考慮して繁雑な式を導出すべきだろうが)、
ここではまず簡単な問題として、上記の変形が無視できるような
「非常に細長い棒が、ちょっとだけ曲がる」
場合に限定して考えたい。
という訳で次の2つの仮定を設けることにする。
なお、
このテキストの方針で
梁の細長い軸に沿って$z$軸を取り、下にたわむ方向に$y$軸を取る。
割と太短い棒の場合、図のように棒の側面に直角な枡目を描いておいて
曲げてやると、曲げを受ける平面内でせん断変形が生じて枡目の角は直角では
なくなるだろう。また棒の断面についても、
例えば引っ張られる上辺は軸方向に伸びたぶん幅方向には縮んだり、
圧縮される下辺は軸方向に縮んだぶん幅方向には膨れたりといった変形も
生じるかも知れない。
これらの変形を考慮すると式の導出がなかなか繁雑になってしまうので
(もちろん、それらを考慮すべき場合は、
考慮して繁雑な式を導出すべきだろうが)、
ここではまず簡単な問題として、上記の変形が無視できるような
「非常に細長い棒が、ちょっとだけ曲がる」
場合に限定して考えたい。
という訳で次の2つの仮定を設けることにする。
なお、
このテキストの方針で
梁の細長い軸に沿って$z$軸を取り、下にたわむ方向に$y$軸を取る。

 図のように初期状態で梁の
ある断面にある任意点$A$が、梁が外力を受けて変形した後、
$A'$に移動したとするとき、
図のように初期状態で梁の
ある断面にある任意点$A$が、梁が外力を受けて変形した後、
$A'$に移動したとするとき、
 上式の$\theta(z)$は、
初期状態では水平だった(座標$z$での)図心軸
(初等梁では断面の法線と一致)が、
変形後に$x$軸の右ねじまわり(図を見ている人にとっては左回りに)
何ラジアン回転したかを示している。
ここでは、
上式の$\theta(z)$は、
初期状態では水平だった(座標$z$での)図心軸
(初等梁では断面の法線と一致)が、
変形後に$x$軸の右ねじまわり(図を見ている人にとっては左回りに)
何ラジアン回転したかを示している。
ここでは、
 $w'(z_{A})$や$v''(z_{A})$は定数であるから、
$\varepsilon_{zz}$は$y$と線形関係にあり、
$-v''(z_{A})$がその傾き、
$w'(z_{A})$が$z$軸の切片を表している。
つまり、
$w'(z_{A})$や$v''(z_{A})$は定数であるから、
$\varepsilon_{zz}$は$y$と線形関係にあり、
$-v''(z_{A})$がその傾き、
$w'(z_{A})$が$z$軸の切片を表している。
つまり、
 上の図のように、梁の断面上にひずみ(や次回やる応力など)の分布を
重ねて描くということはよくやられるが、
慣れないとちょっとわかりにくいかもしれないので、補足する。
図の断面$z=z_{A}$上に$y$軸を持ってきて、
$z$軸を$\varepsilon_{zz}$としてグラフを描いているということである。
上の図のように、梁の断面上にひずみ(や次回やる応力など)の分布を
重ねて描くということはよくやられるが、
慣れないとちょっとわかりにくいかもしれないので、補足する。
図の断面$z=z_{A}$上に$y$軸を持ってきて、
$z$軸を$\varepsilon_{zz}$としてグラフを描いているということである。