注意:
このページの数式は、
MathJaxを使って書いてます。
数式部分がおかしい場合は、更新ボタンをクリックすると
改善するかも知れません。
太文字のギリシャ文字($\mathbf{\sigma}$など)が、
太文字になっていない($\sigma$)かもしれません。
印刷版で確認して下さい。
その他、おかしい記述があると思ったら、
メールなどで指摘して下さい。
梁の支配微分方程式の章で、
梁の支配微分方程式が
$-EI\frac{d^{4}v(z)}{dz^{4}}+q(z)=0$
とたわみの4解微分と分布外力の関係で表されることが示された。
ということは、曲げモーメント分布が力のつりあいから求められない
不静定梁でも
この式を4回積分するとたわみ$v$の一般解が得られるから、
あとは、積分定数を境界条件や連続条件やその他の条件から連立方程式を
立てて解いてやれば、不静定梁でもたわみの式が求まりそうである。
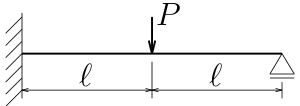 という訳で、
図のような左端固定、右端ローラー支承で中央に集中荷重を受ける不静定梁について、
上の4階の微分方程式を使ってたわみを求めてみる。
梁の左端を原点として梁軸に沿って右側正に$z$軸を取る。
便宜上、
$0<z <\ell $
の左半分のたわみを$v_{左}$と書いて、
$\ell <z<2\ell $
の右半分のたわみを$v_{右}$と書くことにし、
$\frac{d}{dz}$の微分を$'$で表すと、分布外力がないので、
という訳で、
図のような左端固定、右端ローラー支承で中央に集中荷重を受ける不静定梁について、
上の4階の微分方程式を使ってたわみを求めてみる。
梁の左端を原点として梁軸に沿って右側正に$z$軸を取る。
便宜上、
$0<z <\ell $
の左半分のたわみを$v_{左}$と書いて、
$\ell <z<2\ell $
の右半分のたわみを$v_{右}$と書くことにし、
$\frac{d}{dz}$の微分を$'$で表すと、分布外力がないので、
$EIv_{左}''''=0\;\;\;\;(0<z <\ell )$
$EIv_{右}''''=0\;\;\;\;(\ell <z<2\ell )$
それぞれ$z$について
4回積分してみると、
$0<z <\ell $
について
$EIv''''_{左}=0$
$EIv'''_{左}=A$
$EIv''_{左}=Az+B$
$EIv'_{左}=\frac{A}{2}z^{2}+Bz+C$
$EIv_{左}=\frac{A}{6}z^{3}+\frac{B}{2}z^{2}+Cz+D$
$\ell <z<2\ell $
について
$EIv''''_{右}=0$
$EIv'''_{右}=F$
$EIv''_{右}=Fz+G$
$EIv'_{右}=\frac{F}{2}z^{2}+Gz+H$
$EIv_{右}=\frac{F}{6}z^{3}+\frac{G}{2}z^{2}+Hz+J$
となる。積分定数が$A,B,C,D,F,G,H,J$の8個あるので、
条件式が8個必要である。
まず境界条件として使えるのは、
左の固定端でたわみとたわみ角が0つまり
$v_{左}(0)=0$,
$v'_{左}(0)=0$
と
右のローラー支承でたわみとモーメントが0つまり
$v_{右}(2\ell )=0$,
$v''_{右}(2\ell )=0$
の4つの条件で、これらの条件から、
$C=0$
$D=0$
$G=-2F\ell $
$J=\frac{8}{3}F\ell^{3}-2H\ell $
となる。
これらを代入して式を書き直すと、
$0<z <\ell $
について
$EIv''''_{左}=0$
$EIv'''_{左}=A$
$EIv''_{左}=Az+B$
$EIv'_{左}=\frac{A}{2}z^{2}+Bz$
$EIv_{左}=\frac{A}{6}z^{3}+\frac{B}{2}z^{2}$
$\ell <z<2\ell $
について
$EIv''''_{右}=0$
$EIv'''_{右}=F$
$EIv''_{右}=Fz-2F\ell $
$EIv'_{右}=\frac{F}{2}z^{2}-2F\ell z+H$
$EIv_{右}=\frac{F}{6}z^{3}-F\ell z^{2}+Hz+\frac{8}{3}F\ell^{3}-2H\ell $
となる。
連続条件として使えるのは、
中央の集中荷重載荷部で、たわみとたわみ角が等しい、つまり
$v_{左}(\ell )=v_{右}(\ell )$
$v'_{左}(\ell )=v'_{右}(\ell )$
の2つの条件で、これらの条件から、
$\frac{A}{2}\ell^{2}+B\ell +\frac{3F}{2}\ell^{2}=H$と
$\frac{A}{6}\ell^{2}+\frac{B}{2}\ell -\frac{11}{6}F\ell^{2}=-H$
の2式が求まり、辺々足して整理すると、
$4A\ell +9B-2F\ell =0$
となる。
さて、未知数8個に対して境界条件4つと、連続条件2つ使ったが、
あと2つの条件式が必要である。
ここで、中央の集中荷重載荷部の微小部分を図のように薄くスライスして
切り取ってみる。
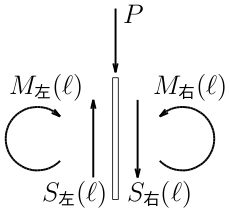 この微小部分の左の切断面にはせん断力$S_{左}(\ell )$と
曲げモーメント$M_{左}(\ell )$が作用し、
右の切断面にはせん断力$S_{右}(\ell )$と
曲げモーメント$M_{右}(\ell )$が作用し、
微小部分に集中荷重外力$P$が作用している。
この微小部分の左の切断面にはせん断力$S_{左}(\ell )$と
曲げモーメント$M_{左}(\ell )$が作用し、
右の切断面にはせん断力$S_{右}(\ell )$と
曲げモーメント$M_{右}(\ell )$が作用し、
微小部分に集中荷重外力$P$が作用している。
この集中荷重外力が作用する微小部分のつりあい条件を考えると
鉛直方向の力のつりあい(下+): $-S_{左}(\ell )+P+S_{右}(\ell )=0$
となる。また、このスライスの厚さが0だとしてモーメントの
つりあいを考えると
モーメントのつりあい(左まわり正): $-M_{左}(\ell )+M_{右}(\ell )=0$
となる。
せん断力は$S=-EIv'''$と曲げモーメントは$M=-EIv''$とそれぞれ関係づけられるから
、
これらのつりあい条件は、
$-(-EIv_{左}'''(\ell ))+P+(-EIv_{右}'''(\ell ))=0$
$-(-EIv_{左}''(\ell ))+(-EIv_{右}''(\ell ))=0$
と書け、残りの2つの条件式が得られる。
これらの式から
$A=F-P$
$A\ell +B=-F\ell $
が得られる。
まず、
$4A\ell +9B-2F\ell =0$
$A=F-P$
$A\ell +B=-F\ell $
の$A,B,F$についての連立方程式を解けば、
$B=\frac{3}{8}P\ell $
$F=\frac{5}{16}P$
$A=-\frac{11}{16}P$
が求まる。すると、
$H=\frac{A}{2}\ell^{2}+B\ell +\frac{3F}{2}\ell^{2}=\frac{P\ell^{2}}{2}$と
$G=-2F\ell =-\frac{5}{8}P\ell $
が求まり、
$J=\frac{8}{3}F\ell^{3}-2H\ell =-\frac{P\ell^3}{6}$
が求まる。
よって、
$v_{左}(z)=\frac{P}{96EI}(-11z^{3}+18\ell z^{2})
\;\;\;\;(0<z <\ell )$
$v_{右}(z)=\frac{P}{96EI}(5z^{3}-30\ell z^{2}+48\ell^{2}z-16\ell^{3})
\;\;\;\;(\ell <z<2\ell )$
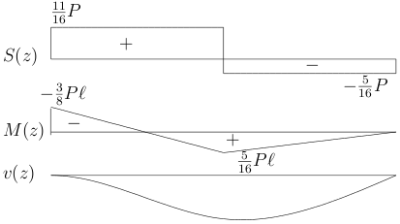
せん断力は、
$S_{左}(z)=-EIv_{左}'''(z)=-A=\frac{11}{16}P
\;\;\;\;(0<z <\ell )$
$S_{右}(z)=-EIv_{右}'''(z)=-F=-\frac{5}{16}P
\;\;\;\;(\ell <z<2\ell )$
曲げモーメントは、
$M_{左}(z)=-EIv_{左}''(z)=-Az-B=\frac{P}{16}(11z-6\ell )
\;\;\;\;(0<z <\ell )$
$M_{右}(z)=-EIv_{右}''(z)=-Fz-G=\frac{5P}{16}(-z+2\ell )
\;\;\;\;(\ell <z<2\ell )$
$M_{左}(\ell )=M_{右}(\ell )=\frac{5}{16}P\ell $
メモ:
 という訳で、
図のような左端固定、右端ローラー支承で中央に集中荷重を受ける不静定梁について、
上の4階の微分方程式を使ってたわみを求めてみる。
梁の左端を原点として梁軸に沿って右側正に$z$軸を取る。
便宜上、
$0<z <\ell $
の左半分のたわみを$v_{左}$と書いて、
$\ell <z<2\ell $
の右半分のたわみを$v_{右}$と書くことにし、
$\frac{d}{dz}$の微分を$'$で表すと、分布外力がないので、
という訳で、
図のような左端固定、右端ローラー支承で中央に集中荷重を受ける不静定梁について、
上の4階の微分方程式を使ってたわみを求めてみる。
梁の左端を原点として梁軸に沿って右側正に$z$軸を取る。
便宜上、
$0<z <\ell $
の左半分のたわみを$v_{左}$と書いて、
$\ell <z<2\ell $
の右半分のたわみを$v_{右}$と書くことにし、
$\frac{d}{dz}$の微分を$'$で表すと、分布外力がないので、
 この微小部分の左の切断面にはせん断力$S_{左}(\ell )$と
曲げモーメント$M_{左}(\ell )$が作用し、
右の切断面にはせん断力$S_{右}(\ell )$と
曲げモーメント$M_{右}(\ell )$が作用し、
微小部分に集中荷重外力$P$が作用している。
この微小部分の左の切断面にはせん断力$S_{左}(\ell )$と
曲げモーメント$M_{左}(\ell )$が作用し、
右の切断面にはせん断力$S_{右}(\ell )$と
曲げモーメント$M_{右}(\ell )$が作用し、
微小部分に集中荷重外力$P$が作用している。
