
構造力学Iオンライン授業用テキスト
第12回オンライン授業
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
 今回からまた新しいことをやる。
今までは、梁の任意点$z$でのせん断力とか曲げモーメントを
$z$の関数として、$S(z)$とか$M(z)$で表した。
今回は、荷重が移動したらどうなるかということを考える。
荷重が梁の左端($z=0$)から右端($z=\ell$)まで移動したとき、
ある点C($z=z_{C}$)のせん断力$S(z_{C})$や
曲げモーメント$M(z_{C})$は、
荷重の移動に応じて変化する。
それを、荷重の位置の関数として表したものを影響線関数といい、
影響線関数をグラフにしたものを影響線という。
今回は、簡単のため、反力の影響線を考える。
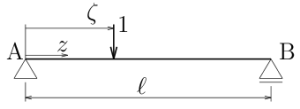
図のような単純梁の反力は、
$V_{A}$と$V_{B}$だが、
$V_{A}$は点A($z=0$)での反力だし、
$V_{B}$は点B($z=\ell$)での反力だから、
$z$の着目点が決まっているので、せん断力や曲げモーメントの影響線よりは、
わかりやすいと思う。
今回からまた新しいことをやる。
今までは、梁の任意点$z$でのせん断力とか曲げモーメントを
$z$の関数として、$S(z)$とか$M(z)$で表した。
今回は、荷重が移動したらどうなるかということを考える。
荷重が梁の左端($z=0$)から右端($z=\ell$)まで移動したとき、
ある点C($z=z_{C}$)のせん断力$S(z_{C})$や
曲げモーメント$M(z_{C})$は、
荷重の移動に応じて変化する。
それを、荷重の位置の関数として表したものを影響線関数といい、
影響線関数をグラフにしたものを影響線という。
今回は、簡単のため、反力の影響線を考える。
図のような単純梁の反力は、
$V_{A}$と$V_{B}$だが、
$V_{A}$は点A($z=0$)での反力だし、
$V_{B}$は点B($z=\ell$)での反力だから、
$z$の着目点が決まっているので、せん断力や曲げモーメントの影響線よりは、
わかりやすいと思う。
梁の左端から右端に移動する荷重として、大きさが 1 の単位荷重を与える。
荷重の位置を表すために、
$z$とは別の座標$\zeta$(ギリシャ文字のzに相当して、読み方は、
ゼータとかツェータとか。書き方は好きなように書いて下さい。
私はひらがなの「ち」を一筆で書くように書くけど)を使う。
テキストによっては、影響線の荷重位置を表す座標も、
せん断力$S(z)$や曲げモーメント$M(z)$の$z$と同じ記号を
使っているものも多いが、それは混乱の原因になるので、
明らかに違う記号で区別した方がいい。
そうすれば、例えば$z=\frac{\ell}{2}$におけるせん断力の影響線を
$\zeta$の関数として$S(z=\frac{\ell}{2},\zeta)$と表すこともできるし、
更に
任意点$z$の影響線を$z$と$\zeta$の関数として$S(z,\zeta)$と表すこともできる。
$z'$みたいな記号で$z$と区別するテキストもあるかもしれないが、
微分と紛らわしいのは避けたい。
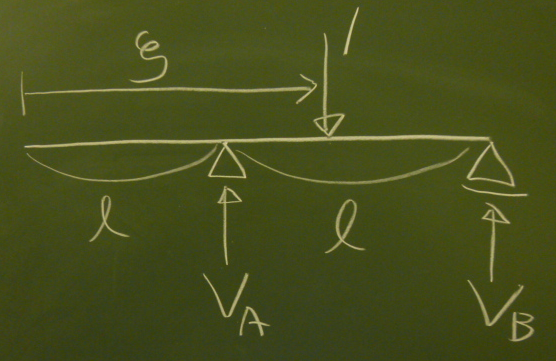
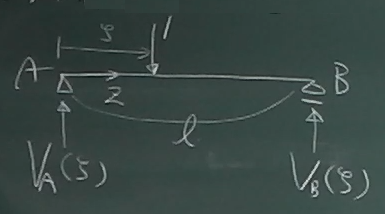 では、図のような単純梁の反力の$V_{A}, V_{B}$の影響線関数を考える。
$V_{A}$は$z=0$での値だし、
$V_{B}$は$z=\ell$での値だから、
$\zeta=0$から$\zeta=\ell$まで荷重が移動するときの$V_{A}, V_{B}$の影響線関数は、
厳密には、$V_{A}(z=0,\zeta)\;, V_{B}(z=\ell,\zeta)$と書くべきだろうが、
$V_{A}$は$z=0$での値だし、
$V_{B}$は$z=\ell$での値というのは決まっているので、
$V_{A}(\zeta)\;, V_{B}(\zeta)$と書けば十分だろう。
では、図のような単純梁の反力の$V_{A}, V_{B}$の影響線関数を考える。
$V_{A}$は$z=0$での値だし、
$V_{B}$は$z=\ell$での値だから、
$\zeta=0$から$\zeta=\ell$まで荷重が移動するときの$V_{A}, V_{B}$の影響線関数は、
厳密には、$V_{A}(z=0,\zeta)\;, V_{B}(z=\ell,\zeta)$と書くべきだろうが、
$V_{A}$は$z=0$での値だし、
$V_{B}$は$z=\ell$での値というのは決まっているので、
$V_{A}(\zeta)\;, V_{B}(\zeta)$と書けば十分だろう。
反力の影響線は、$\zeta$を定数だと考えてやれば、
普通に力のつりあいで求まる。
$\zeta$は、実際には$\zeta=0$から$\zeta=\ell$まで変化するのだけど、
図のような適当な位置の$\zeta$を$a$とか$b$とかと同じ定数と見なして、
左端から長さ$\zeta$のところに大きさ1の荷重が作用している梁の問題と考えて、
普通に反力を求める。力のつりあいから、
$\sum\downarrow=-V_{A}(\zeta)+1-V_{B}(\zeta)=0$
$\sum_{A}\circlearrowleft=-1\cdot\zeta+V_{B}(\zeta)\ell=0$ よって、
$V_{B}(\zeta)=\frac{\zeta}{\ell}$
$V_{A}(\zeta)=1-\frac{\zeta}{\ell}=\frac{\ell-\zeta}{\ell}$
求まった
$V_{A}(\zeta)=\frac{\ell-\zeta}{\ell}$
$V_{B}(\zeta)=\frac{\zeta}{\ell}$
を$\zeta$の関数と捉えれば、これらが反力の影響線関数である。
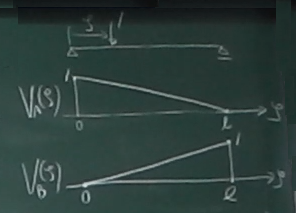 影響線は、影響線関数を$\zeta$を横軸にとって、グラフに描いたものである。
縦軸は反力だが、この授業では反力の影響線は、
せん断力図と合わせて上を正に取ることにする。
$V_{A}(\zeta)$も
$V_{B}(\zeta)$も$\zeta$の1次式で直線のグラフだから、両端の値を求めて
直線で結べばよい。
$V_{A}(\zeta=0)=\frac{\ell-0}{\ell}=1, \;\;$
$V_{A}(\zeta=\ell)=\frac{\ell-\ell}{\ell}=0$
だから、
$V_{A}(\zeta)$は、左端($z=0$)で1で、右端($z=\ell$)で0の直線となる。
荷重1が左端にあれば、左端の反力は荷重1そのものになるから1で、
荷重がだんだん右に移動していけば、左端の反力はだんだん小さくなっていって、
荷重が右端に達したら、左端の反力は0になるということだ。
これは、直感とも対応していると思う。
影響線は、影響線関数を$\zeta$を横軸にとって、グラフに描いたものである。
縦軸は反力だが、この授業では反力の影響線は、
せん断力図と合わせて上を正に取ることにする。
$V_{A}(\zeta)$も
$V_{B}(\zeta)$も$\zeta$の1次式で直線のグラフだから、両端の値を求めて
直線で結べばよい。
$V_{A}(\zeta=0)=\frac{\ell-0}{\ell}=1, \;\;$
$V_{A}(\zeta=\ell)=\frac{\ell-\ell}{\ell}=0$
だから、
$V_{A}(\zeta)$は、左端($z=0$)で1で、右端($z=\ell$)で0の直線となる。
荷重1が左端にあれば、左端の反力は荷重1そのものになるから1で、
荷重がだんだん右に移動していけば、左端の反力はだんだん小さくなっていって、
荷重が右端に達したら、左端の反力は0になるということだ。
これは、直感とも対応していると思う。
$V_{B}(\zeta=0)=\frac{0}{\ell}=0, \;\;$
$V_{B}(\zeta=\ell)=\frac{\ell}{\ell}=1$
だから、
$V_{B}(\zeta)$は、左端($z=0$)で0で、右端($z=\ell$)で1の直線となり、
ちょうど
$V_{A}(\zeta)$とは逆の関係となる。
荷重1が左端にあれば、右端の反力は0で、
荷重がだんだん右に移動していけば、右端の反力はだんだん大きくなっていって、
荷重が右端に達したら、右端の反力は荷重1そのものになるということだ。
これも、直感と対応していると思う。
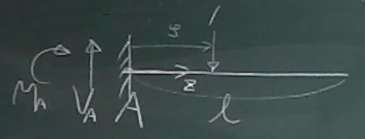 では、同じように片持ち梁の反力の影響線を求めてみよう。
図のような片持ち梁の固定端Aの反力は、
$V_{A}$とモーメント反力の$M_{A}$である。
これらが、$\zeta$の関数で与えられるから、厳密には、
$V_{A}(\zeta)$と$M_{A}(\zeta)$だが、いちいち書くのがめんどくさいので、
$(\zeta)$の部分は計算するときは適宜 省略してもいいだろう。
$\zeta$を定数と考えて普通に力のつりあいを考えると、
第6回でやったのと同様に、
では、同じように片持ち梁の反力の影響線を求めてみよう。
図のような片持ち梁の固定端Aの反力は、
$V_{A}$とモーメント反力の$M_{A}$である。
これらが、$\zeta$の関数で与えられるから、厳密には、
$V_{A}(\zeta)$と$M_{A}(\zeta)$だが、いちいち書くのがめんどくさいので、
$(\zeta)$の部分は計算するときは適宜 省略してもいいだろう。
$\zeta$を定数と考えて普通に力のつりあいを考えると、
第6回でやったのと同様に、
$\sum\downarrow=-V_{A}+1=0$ よって、$V_{A}(\zeta)=1$
$\sum_{A}\circlearrowleft=-M_{A}-1\cdot\zeta=0$ よって、
$M_{A}(\zeta)=-\zeta$
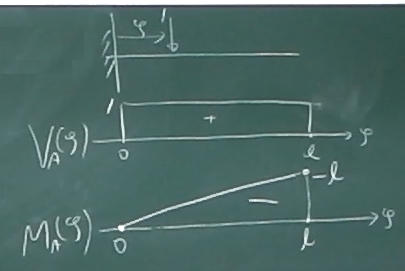 これらをプロットすれば影響線になる。
$V_{A}(\zeta)=1$は定数だから、$0\le \zeta \le\ell$で、常に1である。
これらをプロットすれば影響線になる。
$V_{A}(\zeta)=1$は定数だから、$0\le \zeta \le\ell$で、常に1である。
モーメント反力の影響線は、曲げモーメント図と合わせて、
この授業では下側を正に取ることにする。
$M_{A}(\zeta)=-\zeta$ は、$\zeta$の1次式で直線だから、
$M_{A}(0)=0$と$M_{A}(\ell)=-\ell$を直線で結べばよい。
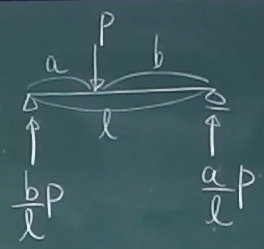 構造力学で静定構造の反力や断面力を求める基本は、あくまで力のつりあいである。
が、集中荷重を受ける単純梁の反力は
頻繁に使うので、つりあいから求めた結果を公式として覚えておくと
便利ではある。
ということで、図のような長さ$\ell$の単純梁を、
長さ$a$と$b$に分ける点に集中荷重$P$が作用している場合の反力を考えてみる。
左端の反力を$V_{A}$, 右端の反力を$V_{B}$とすると、
力のつりあいから
構造力学で静定構造の反力や断面力を求める基本は、あくまで力のつりあいである。
が、集中荷重を受ける単純梁の反力は
頻繁に使うので、つりあいから求めた結果を公式として覚えておくと
便利ではある。
ということで、図のような長さ$\ell$の単純梁を、
長さ$a$と$b$に分ける点に集中荷重$P$が作用している場合の反力を考えてみる。
左端の反力を$V_{A}$, 右端の反力を$V_{B}$とすると、
力のつりあいから
$\sum\downarrow=-V_{A}+P-V_{B}=0$
$\sum_{A}\circlearrowleft=-Pa+V_{B}\ell=0$ よって、$V_{B}=\frac{a}{\ell}P$
$V_{A}=P-\frac{a}{\ell}P=\frac{\ell-a}{\ell}P=\frac{b}{\ell}P$
つまり、長さ$\ell$の単純梁を長さ$a$と$b$に分ける点に集中荷重$P$が作用している
場合の反力は、
$\frac{b}{\ell}P$と
$\frac{a}{\ell}P$になる。
単純梁の長さを$a:b$に分ける点に荷重が作用すれば、
その荷重は、支点で$b:a$に分配されると捉えてもいいだろう。
影響線の反力からもわかるように、
荷重が左端に近づいて$a$が小さくなっていけば、
左端の反力は大きくなっていくわけだから、
長さの比$a:b$と反力の比$b:a$が逆になるのは直感的にも想像しやすい。
 影響線というのは、何のために使うのだろうか。
まあ、橋の上を車が移動したときに、
反力や断面力がどうなるかがわかるということもあるかもしれないけど、
それだけではない。
実は設計計算の際などに大いに役立つ。
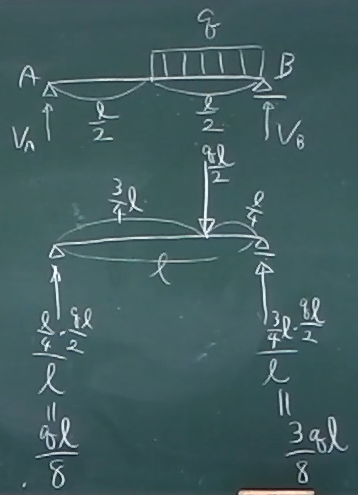
例えば、図のような右半分に等分布荷重が載荷された梁の反力を求めてみてほしい。
力のつりあいから求めるとすれば、
第7回でやったように、
等分布荷重の合計$\frac{q\ell}{2}$を集中荷重に置き換え、
長方形分布の重心の位置に載荷して、それから力のつりあいから
反力を求めなければならない。
それはめんどくさいので、ここでは上の反力の公式を
使って、求めてみると、例えば左端の反力は$\frac{q\ell}{8}$となる。
公式を使ったとしても、ややめんどくさいのではないだろうか。
影響線というのは、何のために使うのだろうか。
まあ、橋の上を車が移動したときに、
反力や断面力がどうなるかがわかるということもあるかもしれないけど、
それだけではない。
実は設計計算の際などに大いに役立つ。
例えば、図のような右半分に等分布荷重が載荷された梁の反力を求めてみてほしい。
力のつりあいから求めるとすれば、
第7回でやったように、
等分布荷重の合計$\frac{q\ell}{2}$を集中荷重に置き換え、
長方形分布の重心の位置に載荷して、それから力のつりあいから
反力を求めなければならない。
それはめんどくさいので、ここでは上の反力の公式を
使って、求めてみると、例えば左端の反力は$\frac{q\ell}{8}$となる。
公式を使ったとしても、ややめんどくさいのではないだろうか。
 さて、単純梁の左端の反力の影響線$V_{A}(\zeta)$は上で求めたが、
これを使って、右半分に等分布荷重が載荷された梁の左端の反力を求めてみよう。
等分布荷重が載荷されている領域$\frac{\ell}{2}\le z\le \ell$に
対応する影響線の面積を求めると、
$\frac{1}{2}\cdot\frac{\ell}{2}\cdot\frac{1}{2}=\frac{\ell}{8}$となる。
これに等分布荷重の$q$をかけた$\frac{q\ell}{8}$が左端の反力となる。
影響線の荷重を単位荷重にしているのは、こういう使い方をするためでもある。
梁の複数の箇所に、異なる大きさの等分布荷重$q_{1}, q_{2},...$が
作用しているような場合にも、
$q_{1}, q_{2},...$に対応する
影響線の面積に$q_{1}, q_{2},...$をかけて足し算することで反力が求まる。
このようなことができるのは、
重ね合わせの原理による。
ちなみに、影響線関数を数学的に捉えるならグリーン関数みたいなものである。
さて、単純梁の左端の反力の影響線$V_{A}(\zeta)$は上で求めたが、
これを使って、右半分に等分布荷重が載荷された梁の左端の反力を求めてみよう。
等分布荷重が載荷されている領域$\frac{\ell}{2}\le z\le \ell$に
対応する影響線の面積を求めると、
$\frac{1}{2}\cdot\frac{\ell}{2}\cdot\frac{1}{2}=\frac{\ell}{8}$となる。
これに等分布荷重の$q$をかけた$\frac{q\ell}{8}$が左端の反力となる。
影響線の荷重を単位荷重にしているのは、こういう使い方をするためでもある。
梁の複数の箇所に、異なる大きさの等分布荷重$q_{1}, q_{2},...$が
作用しているような場合にも、
$q_{1}, q_{2},...$に対応する
影響線の面積に$q_{1}, q_{2},...$をかけて足し算することで反力が求まる。
このようなことができるのは、
重ね合わせの原理による。
ちなみに、影響線関数を数学的に捉えるならグリーン関数みたいなものである。
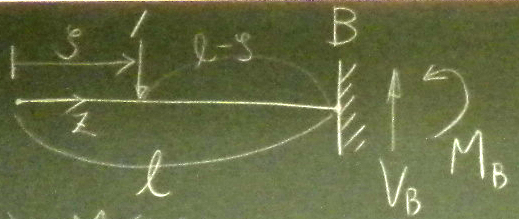 図の片持ち梁について、反力の影響線関数$V_{B}(\zeta), M_{B}(\zeta)$を
求め、その影響線($V_{B}$は上が正、$M_{B}$は下が正)を描け。
答えは、
ここ。
こっちの方が見やすいかも。
図の片持ち梁について、反力の影響線関数$V_{B}(\zeta), M_{B}(\zeta)$を
求め、その影響線($V_{B}$は上が正、$M_{B}$は下が正)を描け。
答えは、
ここ。
こっちの方が見やすいかも。
 図の張り出し梁について、反力の影響線関数$V_{A}(\zeta), V_{B}(\zeta)$を
求め、その影響線(上が正)を描け。
答えは、
ここ。
動画の解説は、
第12回 例題。
図の張り出し梁について、反力の影響線関数$V_{A}(\zeta), V_{B}(\zeta)$を
求め、その影響線(上が正)を描け。
答えは、
ここ。
動画の解説は、
第12回 例題。
 上の問題の答えの補足。
上の問題の図は、
単位荷重が$0\le\zeta\le\ell$の領域にあるときの図で、
モーメントのつりあいもこの状態での点A回りの反時計回りのつりあい
上の問題の答えの補足。
上の問題の図は、
単位荷重が$0\le\zeta\le\ell$の領域にあるときの図で、
モーメントのつりあいもこの状態での点A回りの反時計回りのつりあい
$\sum_{A}\circlearrowleft=1\cdot(\ell-\zeta)+V_{B}\ell=0$から$V_{B}$を求めている。しかし、右の図のように
単位荷重が$\ell\le\zeta\le 2\ell$の領域にある場合は、
モーメントのつりあいが変わって$V_{B}$も変わってしまうような気もする。
ということであれば、
単位荷重が$\ell\le\zeta\le 2\ell$の領域にある場合のつりあいも
ちゃんと考えてみればいいだろう。
点A回りのモーメントのつりあいを考えると、
(上の単位荷重が点Aより左にあった場合は、
単位荷重がつくるモーメントは
反時計回りになったが)単位荷重が点Aより右にある場合は、点Aがつくるモーメントは
時計回りになる。
一方、モーメントの腕の長さは、
(上の単位荷重が点Aより左にある場合は$(\ell-z)$だったが、)
単位荷重が点Aより右にある場合は$(z-\ell)$とこちらも正負が逆になるので、
つまり、右の図のモーメントのつりあいは、
$\sum_{A}\circlearrowleft=-1\cdot(\zeta-\ell)+V_{B}\ell=0$
という式になり、結局、式としては、単位荷重が点Aより左にある場合も右にある
場合も同じ式になる。
2020年度小テスト: 問1, 問2, 問3, 問4, 解答
メモ: