構造力学Iオンライン授業用テキスト
第6回オンライン授業
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
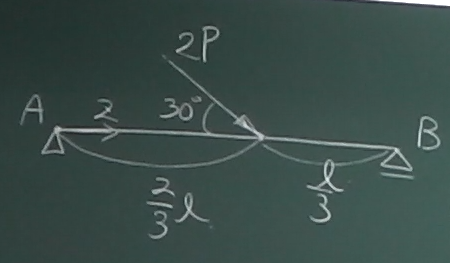前回の例題の3問目で、
図のような梁の断面力を求めた。
まだ求めてない人は、まずは自力で求めておくこと。
式で書いても、梁にどのように分布しているのか、
梁の変形との関係など、イメージがわかないので、
これらの式をグラフに描いてみる。
断面力をグラフとして描いたものは、
N-図、S-図、M-図（まあ、せん断力にQを使う場合は、Q-図とか）みたいに言い、
分野（土木、建築、機械）や国などによっても、
描き方に様々な流儀がある。
ここでは、土木で比較的 一般的な描き方を教える。
まず、求めた断面力は、以下のような$z$の関数である。
$
\ \\
軸力：N(z)=
\begin{cases}
\sqrt{3}P & \;\;\;\;(0\le z \le \frac{2}{3}\ell)\\
0 & \;\;\;\;(\frac{2}{3}\ell\le z \le \ell)
\end{cases}
\ \\
$
$
せん断力：S(z)=
\begin{cases}
\frac{P}{3} & \;\;\;\;(0\le z \le \frac{2}{3}\ell)\\
-\frac{2}{3}P & \;\;\;\;(\frac{2}{3}\ell\le z \le \ell)\\
\end{cases}
\ \\
$
$
曲げモーメント：M(z)=
\begin{cases}
\frac{P}{3}z & \;\;\;\;(0\le z \le \frac{2}{3}\ell) \\
\frac{2}{3}P(\ell-z) & \;\;\;\;(\frac{2}{3}\ell\le z \le \ell)
\end{cases}
\ \\
$
上の断面力は、すべて定数か$z$の1次式だから、
直線だけで描ける簡単なグラフになる。
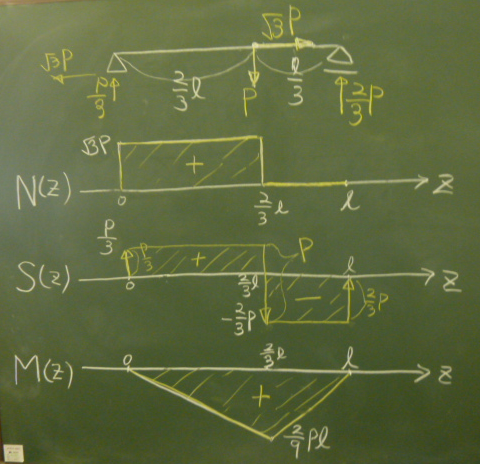まず、$N(z)$とか$S(z)$とか、プロットしたい断面力の記号を書き
（$N$とか$S$とか(z)は省略してもよい）、
その隣に$z$軸を描く。
梁は$z$軸上に横たわっているから、
グラフは梁がある領域(この梁の場合は$0\le z \le\ell)$にしか描かれないことになる
から、横軸を最初から梁の長さぶんしか書かないこともあるし、
$z$と書かないことすらある。
しかし、教育的には、横軸が$z$軸であることをはっきりと意識させた方がよいと
思うので、この授業では、
$z$軸を梁より少し長めに描くことにする。
縦軸は、$N$-図だったら、$N(z)$だし、
$S$-図だったら、$S(z)$なのだが、
縦軸を描くと場所をとって右の図のように縦に各図を並べられなくなるので、
断面力図では、あえて縦軸は描かずに、$z$軸の横に$N$とか$S$と示すことが多い
（ただし、分野によっては縦軸を描く場合もあり、この辺は
あまり本質的なことではない）。
脱線（読まなくてよい）：
今のところ、式を書くときの「書く」と図を描くときの「描く」を
使い分けたりしているが、めんどくさいので、そのうち「書く」に統一するかも
しれない。
もともと日本語の「かく」の語源は、「引っ掻く」から来ており、
そういう意味では、「書く」と「描く」は漢字（要は中国語）の区別であって、
日本語の区別ではない。
私は、自分でしゃべったり書いたりするときに、脳内で
「書く」と「描く」を区別していない。私にとっては同じ概念だ。
似たようなものに、「聞く」「聴く」や「早い」「速い」などがある。
もちろん日本語は漢字を取り入れたおかげで、
多くの造語ができるようになり、大学教育等の高等教育も日本語だけで
行えるようになった
という意味で漢字には感謝しているが、
日本語話者がふだん、日本語の発話の中でまるで区別していない概念を
中国語と同じように区別することにそんなにこだわる必要はない
のではないかと私は思っている。
なので、私の漢字やその他の言葉の使い方はしばしばおかしいと思う。
$
\ \\
軸力：N(z)=
\begin{cases}
\sqrt{3}P & \;\;\;\;(0\le z \le \frac{2}{3}\ell)\\
0 & \;\;\;\;(\frac{2}{3}\ell\le z \le \ell)
\end{cases}
\ \\
$
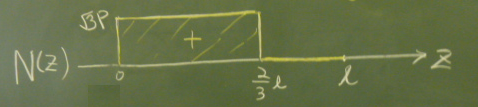
縦軸は描かないものの、
上向きを$N(z)$の正の方向にするか、
下向きを$N(z)$の正の方向にするか決めないといけない。
軸力図は、土木ではあまり使わないので、どちらでもいいが、
この授業では、上側を正とする。
つまり、上向きに$N(z)$軸をとるという意味である。
まず、$N(z)$は、$0\le z \le \frac{2}{3}\ell$で$\sqrt{3}P$で一定だ。
本来の数学的なグラフであれば、
$\sqrt{3}P$の値のある部分にだけ$z$軸に平行に線分を描き入れるのだろうが、
断面力図の場合、見やすいように、図のようにグラフの線を$z$軸と垂直につなげる。
そうすると、グラフの線と$z$軸で囲われた部分ができるが、
ここを更に強調する場合は、斜線を入れたりする。
そして、その領域で値が正なら$+$と、値が負なら$-$と描き入れる。
断面力の正負は、軸力が引張か圧縮かなど力や変形の状態の意味を表すので、
囲われた領域のそれぞれに描き入れる。
$N(z)$は、$\frac{2}{3}\ell\le z \le \ell$では$0$だが、
$0$の場合は、$0$とわかるように、鉛筆で描く場合は、$z$軸上に少し太く線を引く。
領域の境界や、グラフと$z$軸の交点、グラフの極大値などを表すところには、
$z$軸に
$0$, $\frac{2}{3}\ell$, $\ell$のように
$z$座標を記入すること。
この梁は、左端のヒンジ支承は水平方向が拘束されているので、
左端から載荷点まで、一定の引張力が生じている。
右端のローラー支承は水平方向が拘束されていないので、
載荷点を右側に引っ張っても、載荷点から右側には軸力は発生しない。
そういう物理的な意味が、図に描くことで捉えやすくなる。
$
せん断力：S(z)=
\begin{cases}
\frac{P}{3} & \;\;\;\;(0\le z \le \frac{2}{3}\ell)\\
-\frac{2}{3}P & \;\;\;\;(\frac{2}{3}\ell\le z \le \ell)\\
\end{cases}
\ \\
$
せん断力図もこの授業では上側を正とする
（これも分野によって様々な流儀があり、土木でも下側を正とする人も多いが、
後述するように、初学者には、上側が正の方が描きやすいので、
この授業では上側を正としておく）。
$S$-図も$N$-図と同様に描けばよい。
上の$S(z)$は、2つの領域でそれぞれ一定の値だから、
それぞれの値で$z$軸に平行な線を引いて、それを$z$軸とつなげる。
それで囲われた領域に、値に応じて$+$とか$-$と入れて、
鉛筆で描く場合は、うっすらと斜線を入れてもいい。
$z=\frac{2}{3}\ell$の点で$S(z)$が2つの値を持っていることになるが、
前回、領域の境界に$=$を入れるかどうかの際にも話したが、
構造力学では、この辺のことはあまり気にしない。
どうしても気になる人は、領域の境界には$=$を入れないでおいて、
各領域の$S(z)$を、$\lim_{z\to\frac{2}{3}\ell}S(z)$みたいに
極限をとった値を、領域の境界点の$S(z)$の値と定義するとかと捉えてもいいが、
実際の構造物で、1点に集中外力が作用することなんてないし
（面積ゼロの点に力が作用したら圧力は無限だ）、だから、
1点で値がジャンプするなんてことも実際にはない。
そういうものを対象にしているのだから、
数学的厳密性よりも設計や実務の際の便利さの方が優先される。
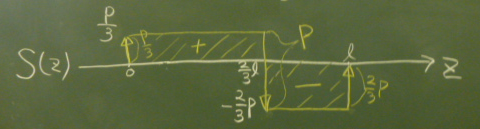
さて、図に変な矢印が描かれているが、せん断力図というのは、
実は、反力や外力をそのままプロットしたものだ。
つまり、実はせん断力$S(z)$を求めなくても、
反力を求めた時点で、せん断力図は描けてしまうのだ。
まず左端の原点には、上向きに$\frac{P}{3}$の反力が作用しているので、
この反力を原点から上向きにそのままプロットする。
そこから$z$軸方向に向かって、せん断力図を描いていくが、
この梁は、$z=\frac{2}{3}\ell$の点までは外力が作用していないので、
外力や反力が作用していない領域では、せん断力は一定に保たれる。
だから、$z=\frac{2}{3}\ell$の点まで、せん断力の線はまっすぐに引く。
$z=\frac{2}{3}\ell$の点に鉛直外力としては$P$が下向きに作用している。
ここで、せん断力の線を$P$だけ下に下げる。
すると、$\frac{P}{3}$の点から$P$だけ下に下がるので、値としては、
$-\frac{2}{3}P$になる。
ここから右に向かって、$z=\ell$までの領域には外力や反力が作用していないので、
ここもせん断力は一定で、そのまままっすぐに線を引いていく。
最後、$z=\ell$のところで上向きに$\frac{2}{3}P$の反力が作用している。
だから、ここから上向きに$\frac{2}{3}P$進むと、
ちょうど$z$軸まで戻る。
このようなせん断力図の描き方は、とても便利で直感的なので、
反力をそのままの向きでプロットできるように、この授業では「上側が正」を採用する。
このような描き方ができるのは、
せん断力$S(z)$と分布荷重$q(z)$(といっても、
分布荷重はまだやっていないが)の間に$q(z)=-S'(z)$の関係があるからだ。
その辺のことは構造力学IIでやる。
さて、前回の授業でせん断力は右下がりが正と
言ったが、このS-図を見ると、左端から載荷点までがプラスで、
載荷点から右側がマイナスだ。物理的には、いったいどういう状況を表しているのだろうか。
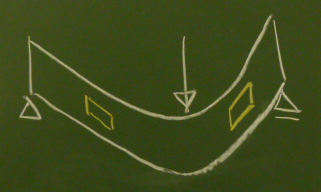図のように、
載荷点より左側では、右下がりのせん断変形をしていて、
載荷点より右側では、右上がりのせん断変形をしているということだ。
載荷点の左右で突然 符号が変わることの意味はこういうことだ。
$
曲げモーメント：M(z)=
\begin{cases}
\frac{P}{3}z & \;\;\;\;(0\le z \le \frac{2}{3}\ell) \\
\frac{2}{3}P(\ell-z) & \;\;\;\;(\frac{2}{3}\ell\le z \le \ell)
\end{cases}
\ \\
$
曲げモーメントに関しては、この授業でも、
土木分野の習慣に従って、下側を正にする。つまり、
下向きに$M(z)$軸を取るという意味である。
これも本質的なことではなく、分野によっては上を正に描くこともあるが、
特に土木構造物の場合、梁とか橋みたいなものは、下にたわむことが多く
(だから、$y$軸も下に取る)、
単純梁のような構造が下にたわんだ場合には、梁の下側が引張になることが多い
（だから、曲げモーメントは、ほぼ世界的に「下側引張が正」である）。
なので、単純梁が下にたわんで、梁の下側が引張になったときに、
グラフも下側に飛び出た方が、グラフと実際の梁の変形が対応していて見やすい
というような意味あいがある。
$N$-図や$S$-図と比べて、$M$-図は、梁の変形（要はたわみ具合）と、
強く関連している。
構造力学IIでやるが、
$M(z)$は、梁の曲率を定数倍したものだ。
だから、
梁の下側が引張で下に凸のときに正となる$M(z)$のプロットが
$M$-図の下側に飛び出して、
梁の上側が引張で上に凸のときに負となる$M(z)$のプロットが
$M$-図の上側に飛び出すように描かれた方が、実際の梁の変形と対応していて、
見やすいということである。
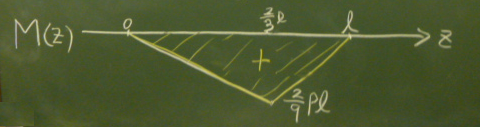
さて、上の$M(z)$は、載荷点の左右、それぞれの領域ともに、
$z$の1次式だから、直線のグラフである。
つまり、各領域の境界の値を求めて、それらを直線で結べばグラフが描けるということだ。
まず、$0\le z \le \frac{2}{3}\ell$の領域の左端$z=0$を、
この領域の式に代入する。すると、
$M(0)=\frac{P}{3}\cdot 0=0$である。
つぎに、$0\le z \le \frac{2}{3}\ell$の領域の右端$z=\frac{2}{3}\ell$を、
この領域の式に代入する。すると、
$M(\frac{2}{3}\ell)=\frac{P}{3}\cdot \frac{2}{3}\ell=\frac{2}{9}P\ell$である。
求まった$(0,0)$と
$(\frac{2}{3}\ell, \frac{2}{9}P\ell)$を直線で結べば、
$0\le z \le \frac{2}{3}\ell$の領域のグラフは描ける。
次に、$\frac{2}{3}\ell\le z \le \ell$の領域の左端$z=\frac{2}{3}\ell$を、
この領域の式に代入する。すると、
$M(\frac{2}{3}\ell )=\frac{2}{3}P(\ell-\frac{2}{3}\ell)=\frac{2}{9}P\ell$となり、
$0\le z \le \frac{2}{3}\ell$の領域の右端での値と同じ値となった。
つまり、この$M(z)$は、上の$S(z)$みたいに、載荷点で急にジャンプしたりしないということだ。
次に、$\frac{2}{3}\ell\le z \le \ell$の領域の右端$z=\ell$を、
この領域の式に代入する。すると、
$M(\ell )=\frac{2}{3}P(\ell-\ell)=0$となる。
求まった
$(\frac{2}{3}\ell, \frac{2}{9}P\ell)$
と
$(0,\ell)$
を直線で結べば、
$\frac{2}{3}\ell \le z \le \ell$の領域のグラフも描ける。
囲われた領域すべてが、正の値であるから、$+$と書き入れ、
強調する場合は、斜線を引く。
曲げモーメントは載荷点$z=\frac{2}{3}\ell$で、
最大値$\frac{2}{9}P\ell$を取り、両端はヒンジで回転できるので、
モーメントは$0$になる。
すべての領域で、正だから、梁は、すべての領域で下側が伸びている
下側が引張の状態である。
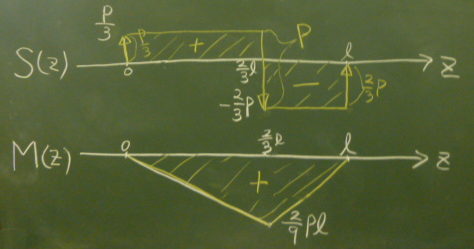さて、曲げモーメント図は、実はせん断力図を見ながら描くことができる。
構造力学IIでやるが、
せん断力は曲げモーメントの微分で表わせ、$S(z)=M'(z)$という関係がある。
つまり、$M(z)$は、$S(z)$を積分したものだということだ。
これを利用して、$M$-図を描いてみる。
まず、左端にモーメント反力はないから、左端の初期値は$0$となる。
$0\le z \le \frac{2}{3}\ell$の領域で、
$S(z)$は正の値で一定だから、ここから$M(z)$は一定の傾き（直線）で
増えていく。どこまで増えるかというと、$S(z)$を
$0\le z \le \frac{2}{3}\ell$の領域で積分した値だから、
この領域の面積を求めればいい
（面積を求める際は、正か負かを区別しておく）。
そうすると、縦$\frac{P}{3}\times$
横$\frac{2}{3}\ell=\frac{2}{9}P\ell$となるから、
$\frac{2}{9}P\ell$まで、まっすぐ増えるということだ。
次に、$\frac{2}{3}\ell \le z \le \ell$の領域は、
$S(z)$は負の値で一定だから、$\frac{2}{9}P\ell$から$M(z)$は一定の傾きで減っていく。
どれだけ減るかというと、$S(z)$を
$\frac{2}{3}\ell \le z \le \ell$の領域をで積分した値だから、
この領域の面積を求めればいい
（面積を求める際は、正か負かを区別しておく）。
そうすると、縦$-\frac{2}{3}P\times$
横$\frac{\ell}{3}=-\frac{2}{9}P\ell$となるから、
$\frac{2}{9}P\ell-\frac{2}{9}P\ell=0$まで戻る。
もし途中にモーメント外力がある場合は、
そこで$M(z)$の値がジャンプする（鉛直外力のある点で$S(z)$がジャンプするように）。
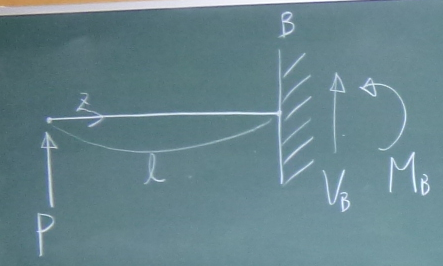
図の梁について、せん断力$S(z)$, 曲げモーメント$M(z)$を
$z$の関数として求め、
$S(z)$-図（上が正）、
$M(z)$-図（下が正）を描け。
水平方向の力は作用していないから、今回は軸力は発生しない。
図の梁のように、壁に埋め込まれた支承は、
固定支承とか固定端といい、鉛直反力、水平反力、モーメント反力の3つの
反力が生じる。
図の梁は左端が固定端で、右端は固定されていない
自由端だから、
反力が3個の静定梁で、力のつりあいで反力や断面力が求まる。
このように一端が壁に固定されている梁を
片持ち
鉛直方向のつりあい(下向き正):$\Sigma\downarrow=-V_{A}+P=0$よって$V_{A}=P$
点Aまわりのモーメントのつりあい(左回り正):
$\sum_{A}\circlearrowleft=-M_{A}-P\ell=0$
よって$M_{A}=-P\ell$
では、断面力を求める。
この梁は、左端に反力が作用し、右端には外力が作用しているが、
それ以外のすべての領域には外力や反力が作用していないから、
$S(z)$や$M(z)$は、
すべての領域$0\le z \le \ell$を場合分けせずに1つの式で表せる。
つまり、
$0\le z \le \ell$の任意点で梁を切り離して、
2つのピースに分け、そのどちらか簡単そうな方を取り出して、
力のつりあいを考えればいい。
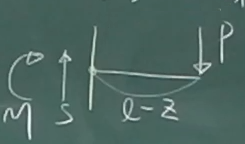今回は、反力を考えなくていい右のピースを取り出す。
鉛直方向のつりあい(下向き正):
$\Sigma\downarrow=-S+P=0$
よって$S(z)=P\;\;\;\;\;(0\le z \le \ell)$
切断点($z$点)
まわりのモーメントのつりあい(左回り正):
$\sum_{z}\circlearrowleft=-M-P(\ell-z)=0$
よって$M(z)=-P(\ell-z)\;\;\;\;\;(0\le z \le \ell)$
$M(z)=P(z-\ell)$と書いてもいいが、
$(\ell-z)$のように正の長さを表すものは、なるべく、
そのまま正の値を表すように書いておいた方が、$M(z)$としては正なのか負なのか
判断しやすい。好みの問題でもある。
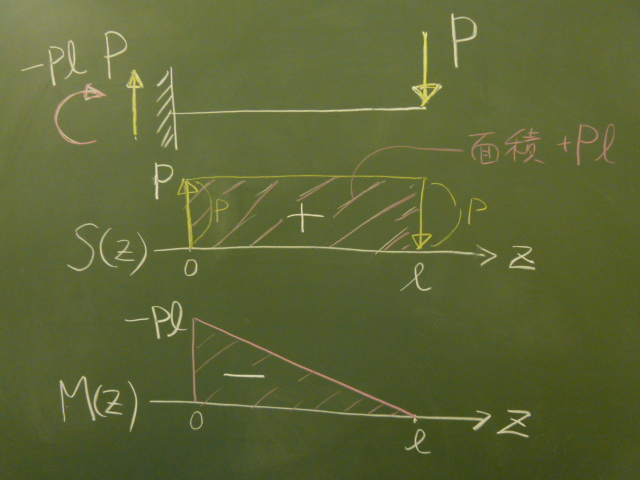まず$S$図は、$S(z)=P$で一定。
反力と外力をそのままプロットという描き方でいくと、
左端で上向き反力$P$だけ持ち上がり、途中は外力がないのでそのまま。
右端で下向き外力$P$だけ下がって$0$に戻る。
次に$M$図。
1次式だから、領域の両端の値を直線で結べばよい。
左端の値は、$M(0)=-P(\ell-0)=-P\ell$で、右端の値は
$M(\ell)=-P(\ell-\ell)=0$. これらを直線で結ぶ。
$S$図を利用して描く場合。
まず、左端にモーメント反力（下側引張を正）として$-P\ell$があるから、
これが初期値になる。
$S$図を見ると、すべての領域で$P > 0$で一定だから、
$M$はこの初期値から、一定の傾きで（直線で）正方向（下）に増えていくことになる。
どれだけ増えるかというと、
$S$図の面積は、縦$P\times$横$\ell=P\ell$だから、
$-P\ell$に$P\ell$を足して、$0$まで戻るということ。
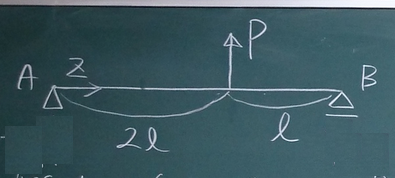
以下の梁について、$S(z)$, $M(z)$を求め、
$S$図（上が正）、$M$図（下が正）を描け。
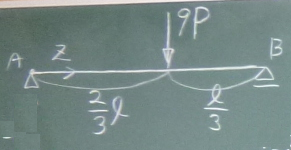
答えは、ここ
答えは、ここ
答えは、ここ
2020年度 小テスト： 問1, 問2, 問3, 問4, 解答
メモ:
答えは、
