構造力学Iオンライン授業用テキスト
第9回オンライン授業
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
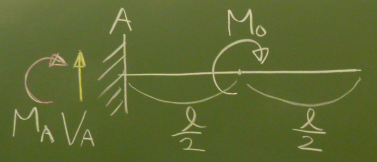図のように、片持ち梁の中央に、$M_{0}$のモーメント外力を受ける梁を
解いてみる。
モーメント外力というのは、その点につまみを取り付けてそのつまみを
ひねっているようなイメージで想像できるだろうか。
まず反力を求める。
$\sum\downarrow=-V_{A}=0$ つまり、$V_{A}=0$
$\sum_{A}\circlearrowleft=-M_{A}-M_{0}=0$ つまり、$M_{A}=-M_{0}$
次に、$S(z), M(z)$を求める。
1点に集中的なモーメント外力を受ける場合は、
集中荷重を受ける場合と同様に、
集中外力や反力の作用していない領域ごとに場合分けする必用がある。
この場合は、
$0\le z\le \frac{\ell}{2}$の領域と、$\frac{\ell}{2}\le z \le \ell$の領域に場合分けしてやればよい。
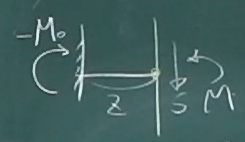まず、$0\le z\le \frac{\ell}{2}$の領域について、
任意の$z$で梁を左右のピースに切り離し、
どちらかのピースを取り出す。今回は左側のピースを取り出して、力のつりあいを
考える。
$\sum\downarrow=S(z)=0\;\;\;\;\;(0\le z\le\frac{\ell}{2})$ $V_{A}=0$だから、鉛直方向の力はない。
$\sum_{z}\circlearrowleft=-(-M_{0})+M=0$ つまり、$M(z)=-M_{0}\;\;\;\;\;(0\le z\le\frac{\ell}{2})$
左端の反力モーメントを下側引張正の向きで$-M_{0}$と書いているが、
反時計回りに$M_{0}$と同じことである。
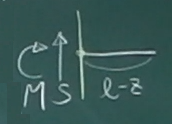次に、$\frac{\ell}{2} \le z \le\ell$の領域について、
任意の$z$で梁を左右のピースに切り離し、
どちらかのピースを取り出す。今回は右側のピースを取り出して、力のつりあいを
考える。
$\sum\downarrow=-S=0$ つまり、$S(z)=0\;\;\;\;\;(\frac{\ell}{2}\le z\le\ell)$
$\sum_{z}\circlearrowleft=-M=0$ つまり、$M(z)=0\;\;\;\;\;(\frac{\ell}{2}\le z\le\ell)$
以上をまとめると、
$S(z)=0\;\;\;\;(0\le z \le \ell)\\$
$
M(z)=
\begin{cases}
-M_{0} & \;\;\;\;(0\le z \le \frac{\ell}{2})\\
0 & \;\;\;\;(\frac{\ell}{2}\le z \le \ell)\\
\end{cases}
\ \\
$
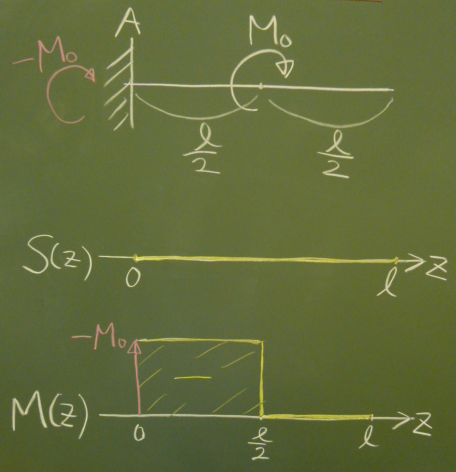$S$図、$M$図を描く。$S(z)$は梁の全長で0だから、
鉛筆で描く場合は、$0$から$\ell$まで少し太く描く。
$M(z)$は、$0$から$\frac{\ell}{2}$までが$-M_{0}$で、
$\frac{\ell}{2}$から$\ell$までが0だ。0の部分は、少し太く描く。
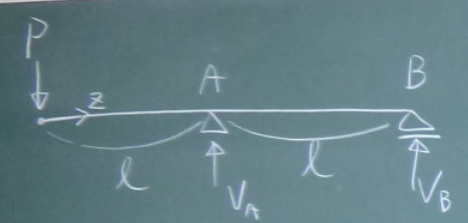
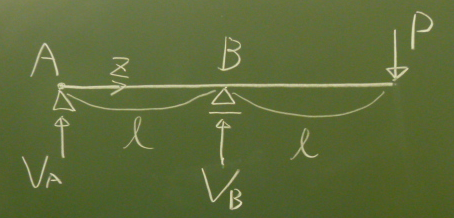図のように、単純梁の一方の先端が支承から張り出しているような梁を
張り出し梁と言う。
点Bで、梁自体にヒンジがあるわけではない。
梁自体にヒンジがついてたら、支点Bで梁の先端は折れ曲がってしまう。
梁は
支点Bのローラー支承の上にのっかているイメージ。
まあ、てこの原理を表す梁と考えてもいい。
点Aが作用点で点Bが支点で張り出した先端が力点みたいに。
まずは反力を求める。
$\sum\downarrow=-V_{A}-V_{B}+P=0$
$\sum_{A}\circlearrowleft=V_{B}\ell-P\cdot 2\ell=0$ よって、$V_{B}=2P$
$V_{A}=-V_{B}+P=-P$
つまり、点Aには下向きにPの反力が作用している
（点Aが上に持ち上げられようとするのを下側に押さえている）。
これを てこと捉えて、張り出し部分をどんどん長くしていったら、
点Aの反力がどれくらい大きくなるか計算してみるのもいいだろう。
次に$S(z), M(z)$を求める。
張り出し梁は、支承のある位置で反力を受けるから、
集中荷重を受ける単純梁の場合と同様に、
少なくとも支点の反力や張り出し部先端の外力の作用していない領域ごとに
場合分けする必用がある。
この場合は、
$0\le z\le \ell$の領域と、
$\ell\le z \le 2\ell$の領域に場合分けしてやればよい。
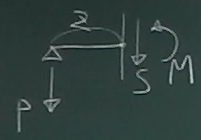まず、$0\le z\le \ell$の領域について、
任意の$z$で梁を左右のピースに切り離し、
どちらかのピースを取り出す。今回は左側のピースを取り出して、力のつりあいを
考える。
$\sum\downarrow=P+S=0$ よって、$S(z)=-P\;\;\;\;\;(0\le z\le\ell)$
$\sum_{z}\circlearrowleft=Pz+M=0$ よって、$M(z)=-Pz\;\;\;\;\;(0\le z\le\ell)$
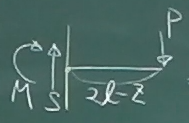次に、$\ell\le z\le 2\ell$の領域について、
任意の$z$で梁を左右のピースに切り離し、
どちらかのピースを取り出す。今回は右側のピースを取り出して、力のつりあいを
考える。
$\sum\downarrow=-S+P=0$ よって、$S(z)=P\;\;\;\;\;(\ell\le z\le2\ell)$
$\sum_{z}\circlearrowleft=-M-P(2\ell-z)=0$ よって、$M(z)=-P(2\ell-z)\;\;\;\;\;(\ell\le z\le2\ell)$
以上をまとめると、
$
S(z)=
\begin{cases}
-P & \;\;\;\;(0\le z \le \ell)\\
P & \;\;\;\;(\ell\le z \le 2\ell)
\end{cases}
\ \\
$
$
M(z)=
\begin{cases}
-Pz & \;\;\;\;(0\le z \le \ell)\\
-P(2\ell-z) & \;\;\;\;(\ell\le z \le 2\ell)
\end{cases}
\ \\
$
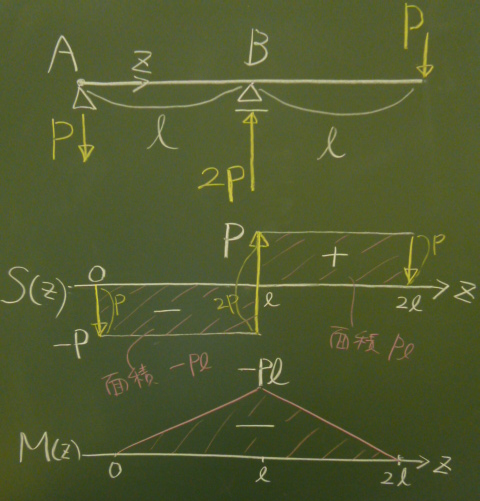$S$図、$M$図を描く。
$S(z)$は、$0$から$\ell$までが$-P$で、
$\ell$から$2\ell$までが$P$、反力をそのままプロットしても描ける。
$M(z)$はどちらの領域でも1次式で直線なので、
領域ごとの境界の値を直線で結べばよい。
まず、$0\le z\le \ell$の領域について、
$M(0)=-P\cdot 0=0, M(\ell)=-P\ell$を直線で結ぶ。
次に、$\ell \le z \le 2\ell$の領域について、
$M(\ell)=-P(2\ell-\ell)=-P\ell$となり、$z=\ell$で
モーメントはジャンプしない。
$M(2\ell)=-P(2\ell-2\ell)=0$ これらを直線で結ぶ。
$S$図の面積を求めて、
S図を積分しながら描いてもよい。
以下の梁について、$S(z)$, $M(z)$を求め、 $S$図（上が正）、$M$図（下が正）を描け。
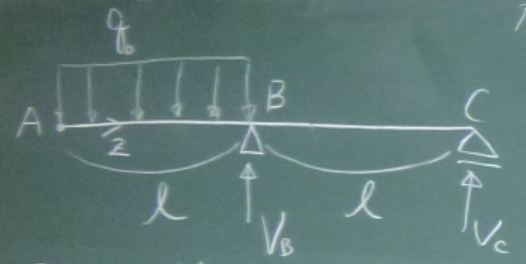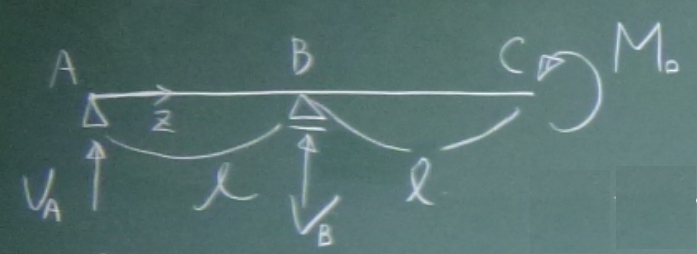答えは、ここ
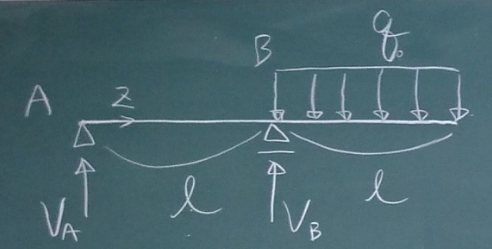答えは、ここ
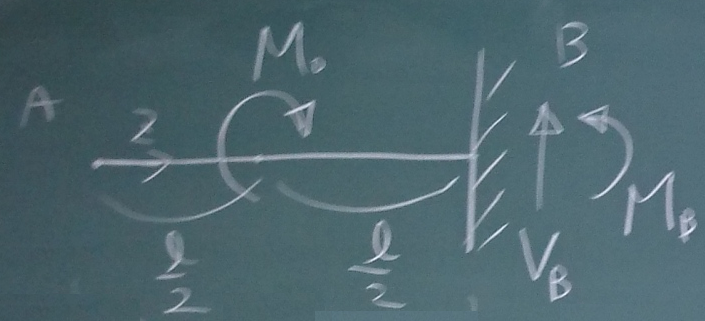答えは、ここ
答えは、ここ
答えは、ここ
2020年度小テスト： 問1, 問2, 問3, 問4, 問5, 解答
メモ:
