構造力学Iオンライン授業用テキスト
第8回オンライン授業
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
前回は、
等分布荷重をやった。
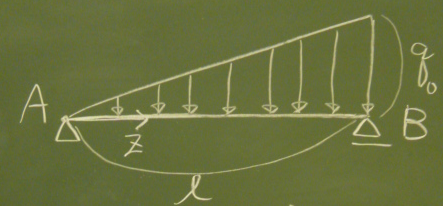
今回は図のような三角形分布荷重をやってみよう。
この荷重は、梁の左端では0で、
右に行くに従って、$z$に比例して増えて、
右端では$q_{0}$の荷重になっている。
今回の分布荷重$q(z)$は定数ではなく、
$z$の関数となっている。
どのように表せるだろうか。
比例の式だから、比例定数を$a$として$q(z)=az$と置いてみれば、
左端では$q(0)=a\times 0=0$で、
右端では$q(\ell)=a\times\ell=q_{0}$だから、
$a=\frac{q_{0}}{\ell}$と求まり、
分布荷重の式は、$q(z)=\frac{q_{0}}{\ell}z$と表されることがわかる。
この式は、梁の全長($0\le z\le \ell$)で成り立つから、
場合分けは不要である。
ちなみに、左端が$q_{0}$で、右端が0の三角形分布の場合は、
$q(z)$は比例の式ではないけど、直線の式だから、
$q(z)=az+b$みたいにおいて、左端、右端の値を代入して$a, b$を
求めればよい。まあ、ちょっと考えれば
そんなことをしなくても左右逆の場合は、
$\frac{q_{0}}{\ell}(\ell-z)$となる。
等分布荷重のとき
と同様にまずは、反力を求めるために分布荷重を集中荷重に置き換える。
まず、分布荷重の合計を求める。
数学的には、$\int_{0}^{\ell}q(z)dz$ということになるが、
要は、三角形の面積を求めればいいから、
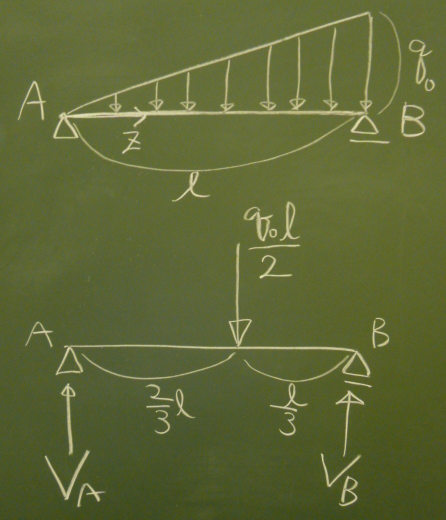
荷重の合計：$\frac{1}{2}\times\ell\times q_{0}=\frac{q_{0}\ell}{2}$
となる。
モーメントのつりあいがくずれないように荷重の合計を一箇所に
載荷するには、
等分布荷重のときと同様に、
分布荷重（今回は三角形分布）の重心（要は三角形の重心）の位置に
作用させればよい。
つまり、$z=\frac{2}{3}\ell$の位置に$\frac{q_{0}\ell}{2}$を作用させる。
この置き換えた梁について反力を求めれば、
それは上の三角形分布荷重の梁の反力と同じになる。
ただし、反力については上の三角形分布と同じになるが、
断面力については同じにならないので注意すること。
さて、力のつりあいから反力を求める。
$\sum\downarrow=-V_{A}+\frac{q_{0}\ell}{2}-V_{B}=0$
$\sum_{A}\circlearrowleft=-\frac{q_{0}\ell}{2}\cdot\frac{2}{3}\ell
+V_{B}\ell=0$
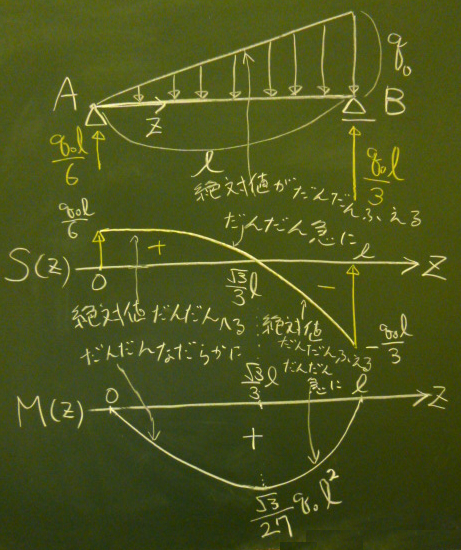
よって、$V_{B}=\frac{q_{0}\ell}{3}, \;V_{A}=\frac{q_{0}\ell}{6}$
等分布荷重のとき
と同様に$S(z), M(z)$を求めるには、
もとの梁を任意の$z$で切り離してつりあいを考える。
反力用に荷重を集中荷重に置き換えた梁のS(z)やM(z)を求めるわけではない
ので注意すること。
もとの梁は、全長($0\le z \le \ell$)で$q(z)$が1つの式$\frac{q_{0}}{\ell}z$で
表されているから、場合分けは不要である
($S(z)$や$M(z)$も全長で1つの式で表せる)。
というわけで、どこで切ってもいいので、適当な$z$で梁を切断して、
2つのパーツに切り離し、今回は左のパーツを取り出してつりあいを考えてみる。
切断面には、
向きに注意して$S, M$を描き込む。
分布荷重のままだと力のつりあいを考えにくいので、
ここで$S, M$を求めるために分布荷重を集中荷重に置き換える。
荷重の合計は、この領域(長さ$z$)の三角形の面積であるが、
切断面($z$点)での荷重の大きさは、
$q(z)=\frac{q_{0}}{\ell}z$に切断点の$z$を代入した値だから、
$\frac{q_{0}}{\ell}z$でいいことになる。
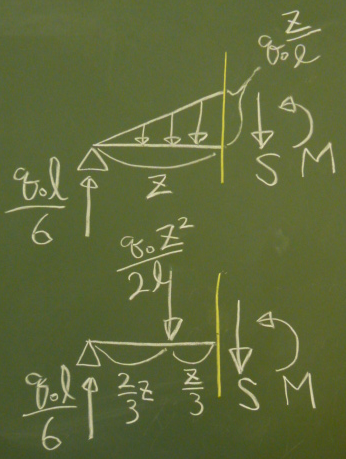
荷重の合計：$\frac{1}{2}\times z\times\frac{q_{0}}{\ell}z=\frac{q_{0}z^{2}}{2\ell}$
この合計した集中荷重をモーメントのつりあいがくずれないように
1箇所に作用させるには、三角形の重心に作用させればよい。
つまり、$z=\frac{2}{3}z$の位置に$\frac{q_{0}z^{2}}{2\ell}$を作用させて
力のつりあいを考える。
$\sum\downarrow=-\frac{q_{0}\ell}{6}+\frac{q_{0}z^{2}}{2\ell}+S=0$
よって、$S(z)=\frac{q_{0}}{6\ell}(-3z^{2}+\ell^{2})\;\;\;\;\;(0\le z\le\ell)$
$\sum_{z}\circlearrowleft=-\frac{q_{0}\ell}{6}z
+\frac{q_{0}z^{2}}{2\ell}\cdot\frac{z}{3}+M=0$
よって、$M(z)=\frac{q_{0}}{6\ell}(-z^{3}+\ell^{2}z)\;\;\;\;\;(0\le z\le\ell)$
3次式とか、式が複雑になってきたら、$M'(z)=S(z)$になるか確かめて検算する。
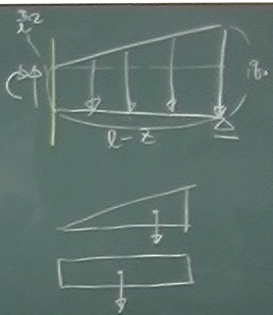もし、右側のパーツを取り出して解くとすると、台形分布を考えなければならなくなる。
台形の面積で荷重の合計を求めて、それを台形の重心に載荷するということでもいいが、
台形の重心を求めるのは、ちょっとめんどくさい（一般的な図形の図心の求め方は、
構造力学IIでやる）。
なので、台形を長方形と三角形に分割して、長方形の面積ぶん荷重を長方形の重心の位置に、
三角形の面積ぶんの荷重を三角形の重心の位置に載荷して考えればよい。
等分布荷重のときの要領で
$S$図、$M$図を描いていきたいが、
今回は$S(z)$も2次式で曲線だし、$M(z)$は3次式だ。まず$S(z)$から。
ひとまず両端の値を求める。
$S(0)=\frac{q_{0}}{6\ell}(-3\cdot 0^{2}+\ell^{2})=\frac{q_{0}\ell}{6}$,
$\;S(\ell)=\frac{q_{0}}{6\ell}(-3\cdot \ell^{2}+\ell^{2})=-\frac{q_{0}\ell}{3}$
反力をそのままプロットという考えでいくと、
左端は上に$\frac{q_{0}\ell}{6}$だし、
右端は上に$\frac{q_{0}\ell}{3}$で0に戻るから、値としては$-\frac{q_{0}\ell}{3}$
でなければならない。
分布荷重は常に下向きだから、初期値$\frac{q_{0}\ell}{6}$から、
常に下に下がり続け、右端では$-\frac{q_{0}\ell}{3}$になっているから、
途中で$z$軸を通過する。
$z$軸との交点も求めておく。
$0=S(z)=\frac{q_{0}}{6\ell}(-3z^{2}+\ell^{2})$とおけば$z=\frac{\sqrt{3}}{3}\ell$
さて、ここまで求めておいて、$S(z)$の傾きが上に凸なのか下に凸なのかを考える。
$M$図が曲線になる場合、
$M'(z)=S(z)$になることを利用して$S$図を見ながら、
$M$図の上に凸か下に凸かを判断することができた。
$S$図が曲線の場合は、
後期の構造力学II第9回でやるが、
$S'(z)=-q(z)$になることを利用して、
分布荷重$q(z)$を見ながら、$S$図の上に凸か下に凸かを以下のように判断する。
今回の例で上記を適用してみる。
これは前回の M図が曲線になるときの描き方と同様の 手順でよい。 まずは両端の値は、両端ヒンジだからどちらもゼロ。
すると、 $M(z)$は$z=\frac{\sqrt{3}}{3}\ell$で最大値を取ることになるから、 その値を計算して記入する。 $M(\frac{\sqrt{3}}{3}\ell)=\frac{q_{0}}{6\ell} (-(\frac{\sqrt{3}}{3}\ell)^{3}+\ell^{2}\cdot\frac{\sqrt{3}}{3}\ell) =\frac{\sqrt{3}}{27}q_{0}\ell^{2}$
以下の梁について、$S(z)$, $M(z)$を求め、
$S$図（上が正）、$M$図（下が正）を描け。
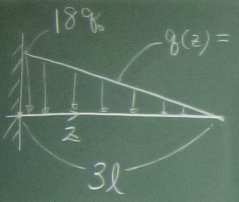答えは、ここ
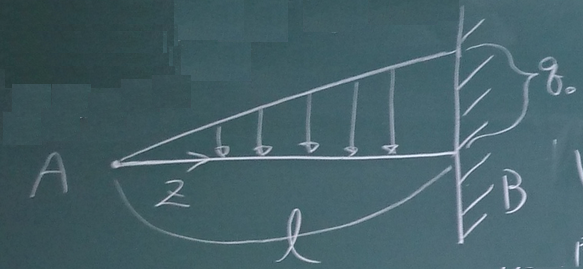答えは、ここ
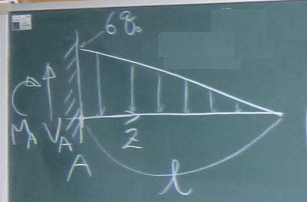答えは、ここ
2020年度 小テスト 問1, 問2, 問3, 問4, 解答
メモ:
