構造力学Iオンライン授業用テキスト
第10回オンライン授業
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
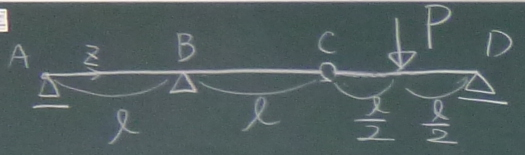図のように、張り出し梁の先端に、ヒンジを挟んでもう1つの梁をくっつけたような梁を
ゲルバー梁という。
これは、張り出し梁の先端に単純梁がのっかていると考えればよい。
実物のイメージは、
"ゲルバー梁"で画像検索
とかしてみてほしい。
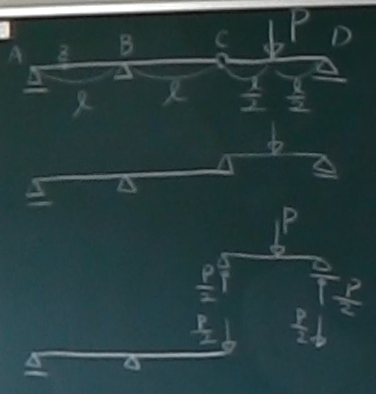どっちに、どっちがのっているかわからなければ、
ヒンジのところで梁を切り離し、梁が自立する方
（この場合は、左側の張り出し梁）を下にして、
切り離されたヒンジ部が、下に落ちてしまう方を単純梁として、上にのっければよい
ということ。
解く順番は、張り出し梁にのっている上の単純梁から解いていく。
この場合、上の単純梁の両端の反力は、左右対称で、
$\frac{P}{2}$ずつだ。
この反力は、ヒンジを介して下の張り出し梁の先端とくっついているから、
作用・反作用の関係から、下の梁の先端には、
下向きに$\frac{P}{2}$の力が作用している。
つまり、上にのっかっている梁（の反力や断面力)が解き終わったら、
下の張り出し梁を、
先端に
$\frac{P}{2}$の外力が作用しているものとして解けばよい。
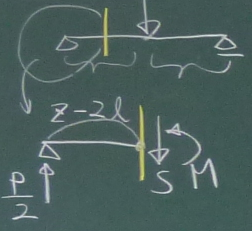上にのっかてる単純梁は、真ん中に集中外力を受けるから、
左端から中央までと、中央から右端までで場合分けすればよい。
さて、$z$軸の原点は、ゲルバー梁の左端(点A)にあるから、上にのってる単純梁の
左端(点C)は、$z=2\ell$ということになる。
つまり、上にのってる梁の左端(点C)から中央(載荷点)までの領域は、
$2\ell \le z\le \frac{5}{2}\ell$ということになる。
この領域の
任意の$z$で梁を左右のピースに切り離し、どちらかのピースを
取り出す。今回は左側のピースを取り出して、力のつりあいを考える。
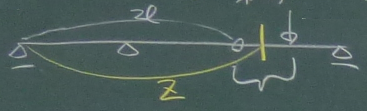取り出した左端から切断点($z$点)までの距離は、図のように
$z-2\ell$であるが、ゲルバー梁とか、
支承が複数あって長くなってくると混乱しやすいので、
梁全体を図に描いて確かめると間違いにくい。
$\sum\downarrow=-\frac{P}{2}+S=0$ よって、$S(z)=\frac{P}{2}\;\;\;\;\;(2\ell \le z\le \frac{5}{2}\ell)$
$\sum_{z}\circlearrowleft=-\frac{P}{2}(z-2\ell)+M=0$ よって、
$M(z)=\frac{P}{2}(z-2\ell)\;\;\;\;\;(2\ell \le z\le \frac{5}{2}\ell)$
次に、
$\frac{5}{2}\ell \le z \le 3\ell$の領域について、
任意の$z$で梁を左右のピースに切り離し、どちらかのピースを
取り出す。今回は右側のピースを取り出して、力のつりあいを考える。
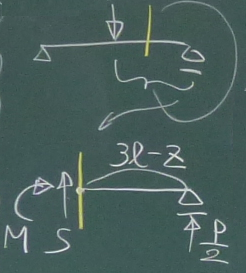
切断点($z$点)から右端(点D)までの距離は、$3\ell-z$であるが、
混乱しそうになったら梁全体を図に描いてみる。
$\sum\downarrow=-S-\frac{P}{2}=0$ よって、
$S(z)=-\frac{P}{2}\;\;\;\;\;(\frac{5}{2}\ell \le z\le 3\ell)$
$\sum_{z}\circlearrowleft=-M
+\frac{P}{2}(3\ell-z)=0$ よって、
$M(z)=\frac{P}{2}(3\ell-z)\;\;\;\;\;(\frac{5}{2}\ell \le z\le 3\ell)$
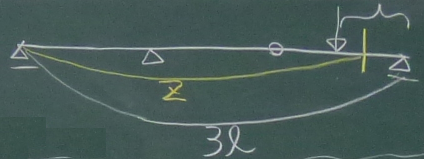
次に、下の張り出し梁を解く。
張り出し梁の先端には、上にのってる梁の反力$\frac{P}{2}$が、
作用・反作用の関係で下向きに作用していると考えればよい。
場合分けは、支点反力や先端の外力の作用していないところを1つの領域と
考えればいいから、$0\le z \le \ell$と$\ell \le z \le 2\ell$で場合分け
すればよい。
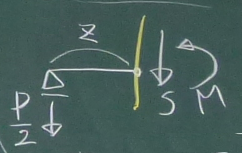まず、$0\le z \le \ell$の領域について、
任意の$z$で梁を左右のピースに切り離し、どちらかのピースを
取り出す。今回は左側のピースを取り出して、力のつりあいを考える。
$\sum\downarrow=\frac{P}{2}+S=0$ よって、
$S(z)=-\frac{P}{2}\;\;\;\;\;(0 \le z\le \ell)$
$\sum_{z}\circlearrowleft=
\frac{P}{2}z+M=0$ よって、
$M(z)=-\frac{P}{2}z\;\;\;\;\;(0 \le z\le \ell)$
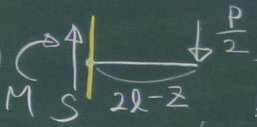次に、$\ell\le z \le 2\ell$の領域について、
任意の$z$で梁を左右のピースに切り離し、どちらかのピースを
取り出す。今回は右側のピースを取り出して、力のつりあいを考える。
$\sum\downarrow=-S+\frac{P}{2}=0$ よって、
$S(z)=\frac{P}{2}\;\;\;\;\;(\ell \le z\le 2\ell)$
$\sum_{z}\circlearrowleft=
-M-\frac{P}{2}(2\ell-z)=0$ よって、
$M(z)=-\frac{P}{2}(2\ell-z)\;\;\;\;\;(\ell \le z\le 2\ell)$
以上をまとめると、
$
S(z)=
\begin{cases}
-\frac{P}{2} & \;\;\;\;(0\le z \le \ell)\\
\frac{P}{2} & \;\;\;\;(\ell \le z \le \frac{5}{2}\ell)\\
-\frac{P}{2} & \;\;\;\;(\frac{5}{2}\ell \le z \le 3\ell)\\
\end{cases}
\ \\
$
$
M(z)=
\begin{cases}
-\frac{P}{2}z & \;\;\;\;(0\le z \le \ell)\\
-\frac{P}{2}(2\ell-z) & \;\;\;\;(\ell \le z \le \frac{5}{2}\ell)\\
\frac{P}{2}(3\ell-z) & \;\;\;\;(\frac{5}{2}\ell \le z \le 3\ell)\\
\end{cases}
\ \\
$
$\ell \le z \le 2\ell$の$S(z), M(z)$の式は、 $2\ell \le z \le \frac{5}{2}\ell$の$S(z), M(z)$の式と同じになったので、 2つの領域をつなげて、 $\ell \le z \le \frac{5}{2}\ell$の領域を1つの式で表している。
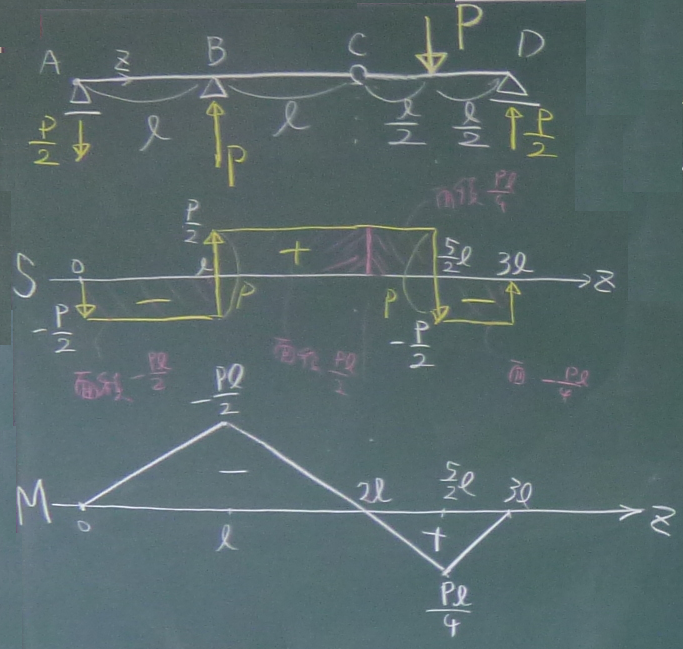$S(z)$はどの領域でも定数だから、
$S$図は、$S(z)$をそのままプロットしてもいいし、
反力・外力をプロットしても、すぐ描ける。
$M(z)$はどの領域でも1次式だから、
各領域の両端の値をプロットしてもいいし、
せん断力図を見ながら、（傾き一定で直線になることはわかるから）
せん断力図の各領域の長方形の面積をプロットしていっても描ける。
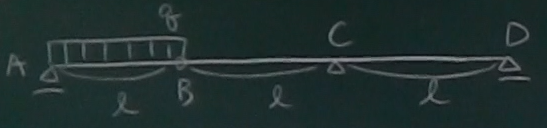図の梁について、$S(z)$, $M(z)$を求め、
$S$図（上が正）、$M$図（下が正）を描け。
答えは、各領域の$S(z)$, $M(z)$を求めたとこまでが
ここ、
それらをまとめてから$S$図、$M$図を描いたのが
ここ。
動画のスクリーンショットなので、画質が悪いが、
上にのっかってる梁は、$0\le z\le \ell$の等分布荷重だから、
第7回の問題と同じ。
動画の解説は、第10回 例題。
メモ:
