
構造力学Iオンライン授業用テキスト
第4回オンライン授業
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
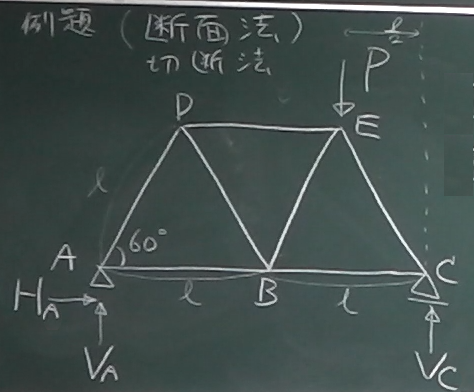 では、図のような正三角形が3つ並んでいる
トラスの部材力を求めてみよう。
反力は3つだから、外的静定で、
力のつりあいだけで反力が求まる。
この問題のように外力が$P$と文字変数で与えられている場合に
反力を求めるというのは、反力を$P$で表すという意味だ。
これは、第2回の要領で解けばいいだろう。
では、図のような正三角形が3つ並んでいる
トラスの部材力を求めてみよう。
反力は3つだから、外的静定で、
力のつりあいだけで反力が求まる。
この問題のように外力が$P$と文字変数で与えられている場合に
反力を求めるというのは、反力を$P$で表すという意味だ。
これは、第2回の要領で解けばいいだろう。
まず鉛直方向のつりあい:
$\Sigma\downarrow=-V_\text{A}+P -V_\text{C} =0$
水平方向のつりあい:
$\Sigma\rightarrow=H_\text{A}=0$
つまり$H_\text{A}=0$で水平反力はないということだ。
モーメントのつりあいは、どの点回りでもいいが、
今回は点C回りで考える。
点Cを回転中心にして、
$V_\text{A}$方向に押すとトラスは右回りするから、
左回りで足し算する場合は$V_\text{A}$がつくるモーメントはマイナス。
点Cを回転中心にして、
$P$方向に押すとトラスは左回転するから、
左回りで足し算する場合は$P$がつくるモーメントはプラス。
($H_\text{A}$は見やすいようにヒンジ支承の下に描かれているが)
$H_\text{A}$の作用点は点Aなので、
作用線上に点Cがあるため、点C回りにはモーメントをつくらない。
$V_\text{C}$も作用線上に点Cがあるから、点C回りにはモーメントをつくらない。
$\Sigma_\text{C}$ $=-V_\text{A}\cdot 2\ell + P\cdot \frac{\ell}{2}=0$
$=-V_\text{A}\cdot 2\ell + P\cdot \frac{\ell}{2}=0$
よって $V_\text{A}=\frac{P}{4}$
これを$-V_\text{A}+P -V_\text{C} =0$に代入し、
$V_\text{C}=\frac{3}{4}P$
さて、反力は求まった。
次に部材力だが、一応、内的静定・不静定を判定すると、
$m=7, r=3, j=5$で$m+r-2j=7+3-2\times 5=0$となり内的静定だから、
力のつりあいだけで部材力が求まるはずである。
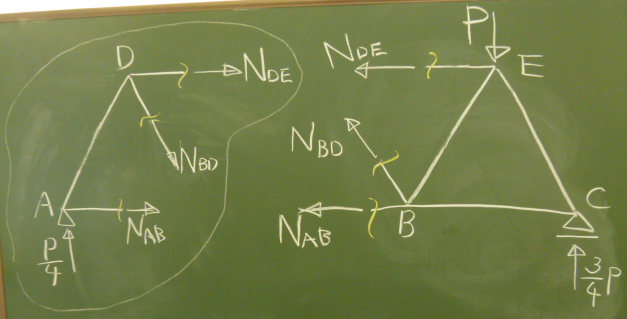 トラスの部材力は、トラス部材の内力としての断面力(軸力)だから、
トラス部材を切らないと見えるようにならない。
トラス部材の切り方は色々とあり得るが、
ここでは、トラス部材を3箇所で切って2つのパーツに切り離す
切断法とか断面法
と呼ばれる方法を教える。
図のように適当な部材3本を切って、
トラスを2つのパーツに切り離してやる。
4本以上 切ると解けなくなるので注意。
そうすると、部材が切られたことにより、それぞれの切断面に、
軸力としての部材力が見えるようになる。
部材力や軸力の定義は一般に引張が正なので、切断面から飛び出る向きに書く。
つまり、圧縮力の場合は符号がマイナスになる。
特定の
トラス部材を表すときは、格点の記号A, B, C, D, E使って、
部材ADとか部材DEみたいに書くが、
部材力についても、部材ADの部材力なら、$N_\text{AD}$,
部材DEの部材力なら、$N_\text{DE}$みたいに書く。
ちなみに、$N_\text{DA}$とか$N_\text{ED}$みたいに書いても
どっちでもいい(部材力は、引張が正という定義なので、
ADとかDAといった方向性に意味はない)。
軸力の記号は$N$を使うことが多いが、
これは、断面に垂直な normal force から来ているのだろうか。
ちなみに、軸力の英語は、axial force.
さて、3箇所で切り離すということなので、例えば部材DE, 部材BD, 部材ABの
3本を切り離して、
その切断面に生じる部材力をそれぞれ、
$N_\text{DE}, N_\text{BD}, N_\text{AB}$とすると、
それぞれの部材力は、切り離された切断面の双方に、
同じ大きさで反対向きに作用している作用・反作用の関係にあるから、
これらの切断面をくっつければ、部材力はプラマイゼロになって、
外力としては見えなくなる。
部材力を求めるというのは、これらの部材力を
外力$P$を用いて表すということだ。
今、トラスを2つのパーツに切り離したが、
これらのそれぞれで力のつりあいが成り立っているから、
そのどちらか簡単そうな方に着目すればよい。
なんとなく左側のパーツの方が簡単そうな感じがするので、
今回は左側のパーツを取り出して、つりあいを考える
(もちろん、右側のパーツでつりあいを考えても構わない)。
トラスの部材力は、トラス部材の内力としての断面力(軸力)だから、
トラス部材を切らないと見えるようにならない。
トラス部材の切り方は色々とあり得るが、
ここでは、トラス部材を3箇所で切って2つのパーツに切り離す
切断法とか断面法
と呼ばれる方法を教える。
図のように適当な部材3本を切って、
トラスを2つのパーツに切り離してやる。
4本以上 切ると解けなくなるので注意。
そうすると、部材が切られたことにより、それぞれの切断面に、
軸力としての部材力が見えるようになる。
部材力や軸力の定義は一般に引張が正なので、切断面から飛び出る向きに書く。
つまり、圧縮力の場合は符号がマイナスになる。
特定の
トラス部材を表すときは、格点の記号A, B, C, D, E使って、
部材ADとか部材DEみたいに書くが、
部材力についても、部材ADの部材力なら、$N_\text{AD}$,
部材DEの部材力なら、$N_\text{DE}$みたいに書く。
ちなみに、$N_\text{DA}$とか$N_\text{ED}$みたいに書いても
どっちでもいい(部材力は、引張が正という定義なので、
ADとかDAといった方向性に意味はない)。
軸力の記号は$N$を使うことが多いが、
これは、断面に垂直な normal force から来ているのだろうか。
ちなみに、軸力の英語は、axial force.
さて、3箇所で切り離すということなので、例えば部材DE, 部材BD, 部材ABの
3本を切り離して、
その切断面に生じる部材力をそれぞれ、
$N_\text{DE}, N_\text{BD}, N_\text{AB}$とすると、
それぞれの部材力は、切り離された切断面の双方に、
同じ大きさで反対向きに作用している作用・反作用の関係にあるから、
これらの切断面をくっつければ、部材力はプラマイゼロになって、
外力としては見えなくなる。
部材力を求めるというのは、これらの部材力を
外力$P$を用いて表すということだ。
今、トラスを2つのパーツに切り離したが、
これらのそれぞれで力のつりあいが成り立っているから、
そのどちらか簡単そうな方に着目すればよい。
なんとなく左側のパーツの方が簡単そうな感じがするので、
今回は左側のパーツを取り出して、つりあいを考える
(もちろん、右側のパーツでつりあいを考えても構わない)。
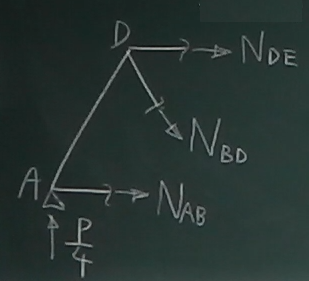 この左側のパーツで、未知数は、
$N_\text{DE}, N_\text{BD}, N_\text{AB}$の3つだ。
そうすると、力のつりあい(鉛直、水平、モーメント)の3つの式で、
これら3つの部材力が求まるはずだ。
やってみよう。
この左側のパーツで、未知数は、
$N_\text{DE}, N_\text{BD}, N_\text{AB}$の3つだ。
そうすると、力のつりあい(鉛直、水平、モーメント)の3つの式で、
これら3つの部材力が求まるはずだ。
やってみよう。
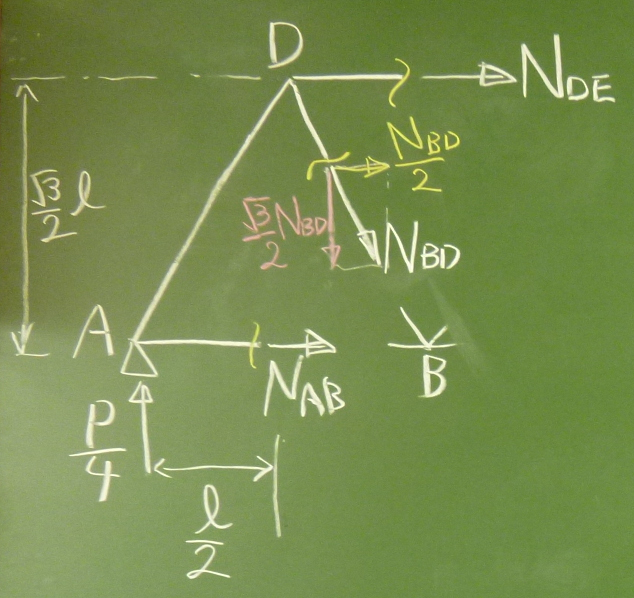 $N_\text{BD}$は、斜めの力だから、
鉛直、水平方向成分に分解してやる。
$N_\text{BD}$は、斜めの力だから、
鉛直、水平方向成分に分解してやる。
まずは鉛直方向のつりあい:
$\Sigma\downarrow=-\frac{P}{4}+\frac{\sqrt{3}}{2}N_\text{BD}=0$
つまり、$N_\text{BD}=\frac{P}{2\sqrt{3}}=\frac{\sqrt{3}}{6}P$
水平方向のつりあい:
$\Sigma\rightarrow=N_\text{DE}+\frac{N_\text{BD}}{2}+N_\text{AB}=0$
モーメントのつりあいは、どの点回りに考えてもよいが、
$N_{BD}$のような斜めの力がモーメントを作らない点回りに考えた方がよい。
ということで、今回は点D回りのモーメントのつりあいを考える。
$N_{BD}$の作用点を切断面として考えると、
分解された鉛直成分や水平成分のそれぞれは、点D回りにモーメントを
つくるが、分解前の$N_{BD}$がモーメントをつくらなければ、
分解されたそれぞれの成分が作るモーメントは、合計すればゼロになる
ということだ(心配な人は、例えば切断点を$\frac{\ell}{2}$とかにして確かめてみよう)。
$N_\text{DE}$も作用線上に点Dがあるから、点D回りのモーメントはつくらない。
そうすると、点D左回りのモーメントは、
点Dを中心にして、
$\frac{P}{4}$方向に押すと右回りだから、
これはマイナスのモーメント。$\frac{P}{4}$の作用線から点Dまでの腕の長さは
$\frac{\ell}{2}$.
点Dを中心にして、
$N_\text{AB}$の方向に押すと左回りだからプラスのモーメント。
$N_\text{AB}$の作用線から点Dまでの腕の長さは$\frac{\sqrt{3}}{2}\ell$.
$\Sigma_\text{D}$ $=-\frac{P}{4}\cdot\frac{\ell}{2}+N_\text{AB}\cdot\frac{\sqrt{3}}{2}\ell=0$
$=-\frac{P}{4}\cdot\frac{\ell}{2}+N_\text{AB}\cdot\frac{\sqrt{3}}{2}\ell=0$
よって $N_\text{AB}=\frac{P}{4\sqrt{3}}=\frac{\sqrt{3}}{12}P$
$N_\text{BD}=\frac{\sqrt{3}}{6}P$と
$N_\text{AB}=\frac{\sqrt{3}}{12}P$
を
$N_\text{DE}+\frac{N_\text{BD}}{2}+N_\text{AB}=0$に代入して、
$N_\text{DE}+\frac{\sqrt{3}}{12}P+\frac{\sqrt{3}}{12}P=0$
よって、$N_\text{DE}=-\frac{\sqrt{3}}{6}P$
このように、
$N_\text{DE}, N_\text{BD}, N_\text{AB}$の3つの部材力が求まる。
ちなみに、
$N_\text{DE}<0, N_\text{BD}>0, N_\text{AB}>0$であるから、
$N_\text{DE}$は圧縮力、$N_\text{BD}$と$N_\text{AB}$は引張力という
ことになる。
ところで、今、鉛直方向のつりあい、水平方向のつりあい、
点Dまわりのモーメントのつりあい、の3つのつりあいの式を使ったが、
他の点まわりにモーメントのつりあいが使えそうだったら、
モーメントのつりあいを2つ以上 使ったって構わない。
しかも、モーメントの中心は、着目しているパーツ内にない点でもよい。
例えば、左側のパーツ内には含まれない点Bまわりのモーメントを
考えてみる。$N_\text{BD}$の作用線は点Bを通るから、$N_\text{BD}$はモーメントを
作らない。$N_\text{AB}$の作用線も点Bを通るから、
$N_\text{AB}$もモーメントを作らない。
そうすると、点$B$まわりにモーメントをつくるのは$N_\text{DE}$一つだけとなり、
連立させなくても一発で$N_\text{DE}$が求まる。
$\Sigma_\text{B}$ $=-\frac{P}{4}\cdot\ell-N_\text{BD}\cdot\frac{\sqrt{3}}{2}\ell=0$
$=-\frac{P}{4}\cdot\ell-N_\text{BD}\cdot\frac{\sqrt{3}}{2}\ell=0$
これなら連立させずに一発で
$N_\text{DE}=-\frac{\sqrt{3}}{6}P$が求まり楽である。
 左側のピースでまだ求まっていない部材力は、$N_\text{AD}$だ。
これを片付けてしまおう。
$N_\text{AD}$を見えるようにするには、部材ADを切らなければならない。
部材ADと部材ABの2箇所を切って、格点Aまわりのパーツを取り出してみる。
$N_\text{AB}=\frac{\sqrt{3}}{12}P$は既に求まっているので、
未知数は$N_\text{AD}$の1つだ。
このパーツについて、鉛直方向、水平方向の力のつりあいが使える。
このパーツに作用するすべての力は、
作用線が点Aを通るのでモーメントのつりあいは使えない。
$N_\text{AD}$は斜めなので、鉛直、水平成分に分解して、
鉛直方向か水平方向のつりあいを考えればよい。
鉛直方向の方が簡単そうなので、今回は鉛直方向のつりあいを考える。
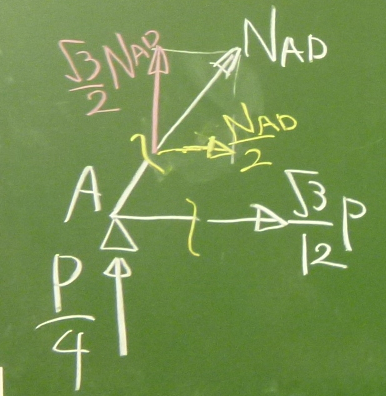
左側のピースでまだ求まっていない部材力は、$N_\text{AD}$だ。
これを片付けてしまおう。
$N_\text{AD}$を見えるようにするには、部材ADを切らなければならない。
部材ADと部材ABの2箇所を切って、格点Aまわりのパーツを取り出してみる。
$N_\text{AB}=\frac{\sqrt{3}}{12}P$は既に求まっているので、
未知数は$N_\text{AD}$の1つだ。
このパーツについて、鉛直方向、水平方向の力のつりあいが使える。
このパーツに作用するすべての力は、
作用線が点Aを通るのでモーメントのつりあいは使えない。
$N_\text{AD}$は斜めなので、鉛直、水平成分に分解して、
鉛直方向か水平方向のつりあいを考えればよい。
鉛直方向の方が簡単そうなので、今回は鉛直方向のつりあいを考える。
$\Sigma\downarrow=-\frac{P}{4}-\frac{\sqrt{3}}{2}N_\text{AD}=0$
$N_\text{AD}=-\frac{P}{2\sqrt{3}}=-\frac{\sqrt{3}}{6}P$
さて、このように、格点まわりの部材をすべて切り離し、
格点まわりのピースだけを取り出して、
鉛直方向、水平方向のつりあいだけを使って部材力を求める方法を
格点法とか節点法
と言う。
今回の場合、
例えば点Bの回りには4本の部材があるから、
4本の部材を切り離して、点B回りのピースを取り出したら、
未知数が4つ
($N_\text{AB}, N_\text{BD}, N_\text{BE}, N_\text{BC}$)となり、
当然、このピースのつりあい
(しかも鉛直、水平の2つ)だけでは部材力は求まらない。
あるいは、点D回りの3本の部材を切り離して、
点D回りのピースを取り出したら、
未知数は3つ
($N_\text{AD}, N_\text{BD}, N_\text{DE}$)だけど、
つりあいの式は鉛直、水平の2つだから、
やはりこのピースだけでは部材力は求まらない。
つまり、格点法というのは、
格点まわりの部材をすべて切り離して、
格点まわりのピースをばらばらにし、
それぞれのピースについて鉛直、水平の2つのつりあいの式をたて、
それらを連立させて解くというやり方だ。
みなさんには、
モーメントのつりあいを有効利用できるようになってほしいので、
まずは、切断法で主要な部材力を求め、
残った部材力を、適宜、格点まわりだけ切り離して求めるという
やり方に慣れてもらえばいいかなと思う。
 残りの部材力を求めよう。
今度は右の方の部材DE, BE, BCの3箇所を切って、2ピースに切り離す。
2ピースのどちらに着目してもいいが、
今回は右側のピースを取り出してつりあいを考える。
$N_\text{BE}$は斜めなので、鉛直、水平成分に分解する。
$N_\text{DE}=-\frac{\sqrt{3}}{6}P$は既にわかっている。
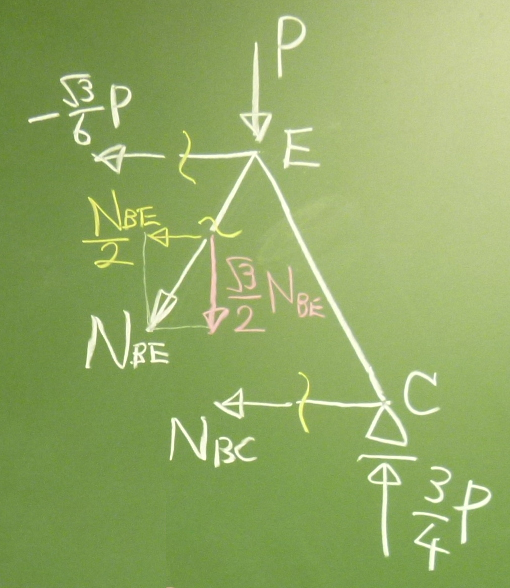
残りの部材力を求めよう。
今度は右の方の部材DE, BE, BCの3箇所を切って、2ピースに切り離す。
2ピースのどちらに着目してもいいが、
今回は右側のピースを取り出してつりあいを考える。
$N_\text{BE}$は斜めなので、鉛直、水平成分に分解する。
$N_\text{DE}=-\frac{\sqrt{3}}{6}P$は既にわかっている。
鉛直方向のつりあい:
$\Sigma\downarrow=P+\frac{\sqrt{3}}{2}N_\text{BE}
-\frac{3}{4}P=0$
よって、$N_\text{BE}=-\frac{P}{2\sqrt{3}}=-\frac{\sqrt{3}}{6}P$
水平方向のつりあい:
$\Sigma\rightarrow=-(-\frac{\sqrt{3}}{6}P)
-\frac{N_\text{BE}}{2}-N_\text{BC}=0$
つまり、
$\frac{\sqrt{3}}{6}P
+\frac{\sqrt{3}}{12}P-N_\text{BC}=0
\\
$
よって
$N_\text{BC}=\frac{\sqrt{3}}{4}P$
 あと求まってない部材力は、$N_{EC}$だけだ。
これは、
格点C回りの部材2本を切り離して考えよう。
$N_\text{BC}=\frac{\sqrt{3}}{4}P$は既に求まっているから、
$N_{EC}$は、斜めの部材力だから鉛直、水平に分解して、
鉛直か、水平、どっちかのつりあいを考えればいい。
これは水平でいくか。
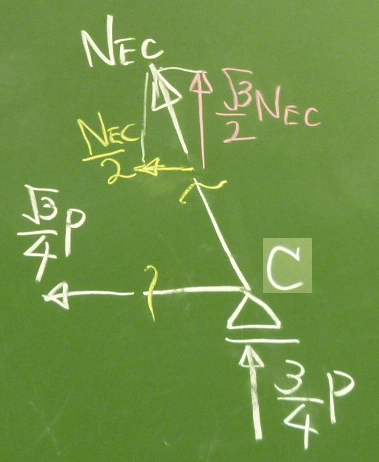
あと求まってない部材力は、$N_{EC}$だけだ。
これは、
格点C回りの部材2本を切り離して考えよう。
$N_\text{BC}=\frac{\sqrt{3}}{4}P$は既に求まっているから、
$N_{EC}$は、斜めの部材力だから鉛直、水平に分解して、
鉛直か、水平、どっちかのつりあいを考えればいい。
これは水平でいくか。
水平方向のつりあい:
$\Sigma\rightarrow=-\frac{\sqrt{3}}{4}P
-\frac{N_\text{EC}}{2}=0$
$N_\text{EC}=
-\frac{\sqrt{3}}{2}P$
これですべての部材の部材力が求まった。
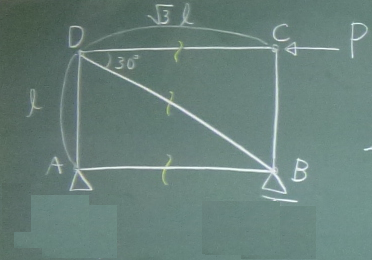 以下のトラスについて切れ目を入れた3本の部材の部材力を求めよ。
以下のトラスについて切れ目を入れた3本の部材の部材力を求めよ。
答えはここ。
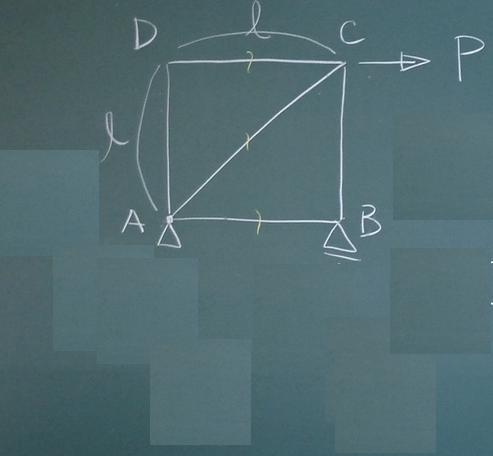 答えはここ。
答えはここ。
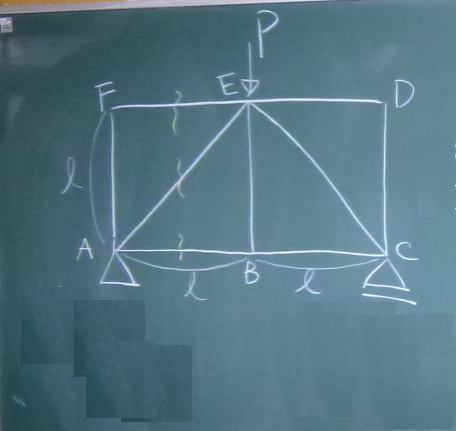 答えはここ。
答えはここ。