
構造力学Iオンライン授業用テキスト
第1回オンライン授業
小さい字は補足説明や余談なので、読み飛ばしてもいいです。
 このテキスト上では、鉛直下方向を$+y$, 水平右方向を$+z$とする$yz$座標を
使っていくことにする。
こんなふうに小さい字で補足説明を書くことにする。
橋や梁のように水平に横たわる
1方向に細長い部材を扱うことの多い
構造力学の座標の取り方には様々な流儀があるが、
鉛直下向きのたわみ方向に$+y$を取るのは一般的だし、
梁軸方向は$x$軸を取る流派が(2次元問題では)多数派だと思うけど、
3次元への拡張を考えた場合、
3つの軸の中で1つだけ特殊な梁軸を$z$軸にしておいた方が何かと便利
(例えば、
横$x$方向のたわみと、
下$y$方向のたわみという具合に、
$x$と$y$の関係は対等になるし、
断面の断面2次モーメントの計算などを$xy$座標で考えられる)
なような気が(今のところ)するので、梁軸を$z$軸にしておく。
3次元の問題で特殊な軸が1つあり、他の2つの軸は対等な場合、
特殊な軸を$x$にするのか、$y$にするのか、$z$にするのかという程度の好みの
問題だ。例えば、
水中や地中や空中の問題を扱う場合、重力の働く高さ方向を$z$軸にとって、
水平面の$x$軸と$y$軸は対等という扱いが多いが、
梁軸(水平が多い)が特殊な梁の場合は、
梁軸を$z$にしたいということ。
物体(まずは変形しない剛体ということにしておこう)に
いろんな向きを向いたいろんな大きさの力がいくつも
(簡単のため3つということにしておこう)
作用していたとする。
このように、物体が外部から受ける力を外力と言う。
力の矢印を図示する場合、座標や変位の矢印とは区別して、
図のように閉じた矢印にすることをおすすめするが、
このテキスト上でも統一されていない...
こういう場合、
2次元の構造力学の問題では、話を簡単にするため、
物体(剛体)に作用する様々な力を、
このテキスト上では、鉛直下方向を$+y$, 水平右方向を$+z$とする$yz$座標を
使っていくことにする。
こんなふうに小さい字で補足説明を書くことにする。
橋や梁のように水平に横たわる
1方向に細長い部材を扱うことの多い
構造力学の座標の取り方には様々な流儀があるが、
鉛直下向きのたわみ方向に$+y$を取るのは一般的だし、
梁軸方向は$x$軸を取る流派が(2次元問題では)多数派だと思うけど、
3次元への拡張を考えた場合、
3つの軸の中で1つだけ特殊な梁軸を$z$軸にしておいた方が何かと便利
(例えば、
横$x$方向のたわみと、
下$y$方向のたわみという具合に、
$x$と$y$の関係は対等になるし、
断面の断面2次モーメントの計算などを$xy$座標で考えられる)
なような気が(今のところ)するので、梁軸を$z$軸にしておく。
3次元の問題で特殊な軸が1つあり、他の2つの軸は対等な場合、
特殊な軸を$x$にするのか、$y$にするのか、$z$にするのかという程度の好みの
問題だ。例えば、
水中や地中や空中の問題を扱う場合、重力の働く高さ方向を$z$軸にとって、
水平面の$x$軸と$y$軸は対等という扱いが多いが、
梁軸(水平が多い)が特殊な梁の場合は、
梁軸を$z$にしたいということ。
物体(まずは変形しない剛体ということにしておこう)に
いろんな向きを向いたいろんな大きさの力がいくつも
(簡単のため3つということにしておこう)
作用していたとする。
このように、物体が外部から受ける力を外力と言う。
力の矢印を図示する場合、座標や変位の矢印とは区別して、
図のように閉じた矢印にすることをおすすめするが、
このテキスト上でも統一されていない...
こういう場合、
2次元の構造力学の問題では、話を簡単にするため、
物体(剛体)に作用する様々な力を、
に置き換えてしまうという操作をやることがある。
例えば、第5回でやる断面力とか。
まずはこれを練習してみる。
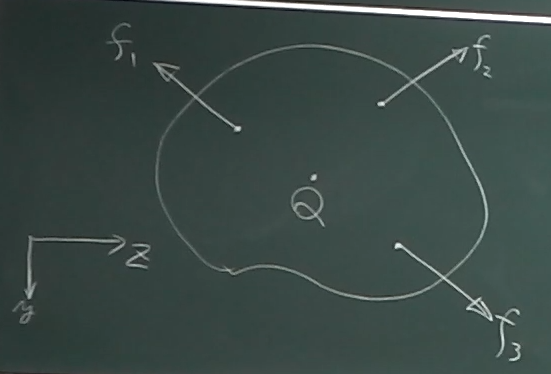
 図のような
$f_{1}$, $f_{2}$, $f_{3}$
を$Q$点に作用する
$y$方向の力、$z$方向の力、左回りのモーメントに置き換えてみよう。
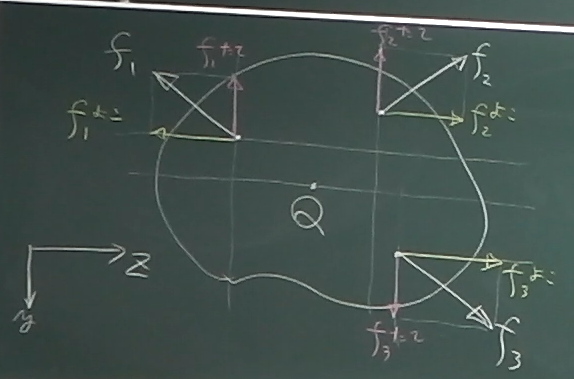
まずは
$f_{1}$, $f_{2}$, $f_{3}$
を図のようにそれぞれ
$f_{1}^{たて}$と$f_{1}^{よこ}$,
$f_{2}^{たて}$と$f_{2}^{よこ}$,
$f_{3}^{たて}$と$f_{3}^{よこ}$
というように
鉛直方向成分$F_{y}$と水平方向成分$F_{z}$に分解してみる。
まず$y$軸方向の力の合計は、$y$軸方向(つまり下向き)が正なので、
下を向いている力にはプラスをつけて、
上を向いている力にはマイナスをつけてから足しあわせると
図のような
$f_{1}$, $f_{2}$, $f_{3}$
を$Q$点に作用する
$y$方向の力、$z$方向の力、左回りのモーメントに置き換えてみよう。
まずは
$f_{1}$, $f_{2}$, $f_{3}$
を図のようにそれぞれ
$f_{1}^{たて}$と$f_{1}^{よこ}$,
$f_{2}^{たて}$と$f_{2}^{よこ}$,
$f_{3}^{たて}$と$f_{3}^{よこ}$
というように
鉛直方向成分$F_{y}$と水平方向成分$F_{z}$に分解してみる。
まず$y$軸方向の力の合計は、$y$軸方向(つまり下向き)が正なので、
下を向いている力にはプラスをつけて、
上を向いている力にはマイナスをつけてから足しあわせると
$y$方向の力の合計: $F_{y}=
\Sigma\downarrow=
(-f_{1}^{たて})+(-f_{2}^{たて})+(+f_{3}^{たて})$
となる。
$\Sigma\downarrow$の記号は、下向きを正として縦方向の力をすべて足し算することを
意味する。
同様に$z$軸方向の力の合計は、$z$軸方向(つまり右向き)が正なので、
右を向いている力にはプラスをつけて、
左を向いている力にはマイナスをつけてから足しあわせると
$z$方向の力の合計: $F_{z}=
\Sigma\rightarrow=
(-f_{1}^{よこ})+(+f_{2}^{よこ})+(+f_{3}^{よこ})$
となる。
$\Sigma\rightarrow$は、右向きを正として横方向の力をすべて足し算する意味である。
もし、これらの力の横方向成分を
$f_{y1}=(-f_{1}^{たて})$, $f_{y2}=(-f_{2}^{たて})$,
$f_{y3}=(+f_{3}^{たて})$
のように正負を軸の向きに合わせて定義すれば、
$F_{y}=\sum_{i=1}^{3} f_{yi}=f_{y1}+f_{y2}+f_{y3}$
のように添字で演算できるように書くこともできる。
 これらの$y$方向の力の合計$F_{y}$と$z$方向の力の合計$F_{z}$は、
物体のどこに作用させるかで回転運動の仕方には違いが出てくるが、
物体の重心に与える加速度は、
点$Q$に作用させても
どこに作用させても同じである。
力を加えられた物体は、物体の重心の回りに回転しながら移動するが、
もし力が重心にのみ加えられるなら回転せずに並進移動する。
ということで、この
$F_{y}$と$F_{z}$
を点$Q$に作用させて
$f_{1}, f_{2}, f_{3}$による並進運動を代表させることにすると、
回転運動に関して
$f_{1}, f_{2}, f_{3}$による作用と同じ作用をする1つのモーメントを
点$Q$に作用させたい。
回転運動に関して
$f_{1}, f_{2}, f_{3}$が作用している状態と同じ作用を
する1つのモーメントを点$Q$に作用させるためには、
$f_{1}, f_{2}, f_{3}$による点$Q$の回りの
モーメントを求めればよい。
点$Q$に作用している$F_{y}$と$F_{z}$は点$Q$回りのモーメントには
関与しない。
点$Q$の回りのモーメントは、
左回り(反時計回り)を正とすると、
点$Q$回りに左回りになるモーメントにはプラスをつけて、
点$Q$回りに右回りになるモーメントにはマイナスをつけて、
たしあわせていくと、
これらの$y$方向の力の合計$F_{y}$と$z$方向の力の合計$F_{z}$は、
物体のどこに作用させるかで回転運動の仕方には違いが出てくるが、
物体の重心に与える加速度は、
点$Q$に作用させても
どこに作用させても同じである。
力を加えられた物体は、物体の重心の回りに回転しながら移動するが、
もし力が重心にのみ加えられるなら回転せずに並進移動する。
ということで、この
$F_{y}$と$F_{z}$
を点$Q$に作用させて
$f_{1}, f_{2}, f_{3}$による並進運動を代表させることにすると、
回転運動に関して
$f_{1}, f_{2}, f_{3}$による作用と同じ作用をする1つのモーメントを
点$Q$に作用させたい。
回転運動に関して
$f_{1}, f_{2}, f_{3}$が作用している状態と同じ作用を
する1つのモーメントを点$Q$に作用させるためには、
$f_{1}, f_{2}, f_{3}$による点$Q$の回りの
モーメントを求めればよい。
点$Q$に作用している$F_{y}$と$F_{z}$は点$Q$回りのモーメントには
関与しない。
点$Q$の回りのモーメントは、
左回り(反時計回り)を正とすると、
点$Q$回りに左回りになるモーメントにはプラスをつけて、
点$Q$回りに右回りになるモーメントにはマイナスをつけて、
たしあわせていくと、
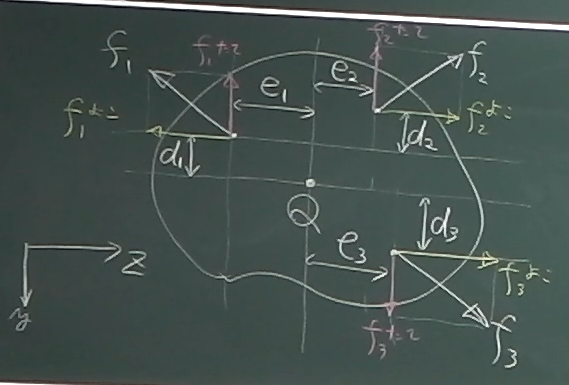
点$Q$回りのモーメントの合計:
$M_{Q}=\Sigma_{Q}$ $=-f_{1}^{たて}e_{1}+f_{1}^{よこ}d_{1}
+f_{2}^{たて}e_{2}-f_{2}^{よこ}d_{2}
-f_{3}^{たて}e_{3}+f_{3}^{よこ}d_{3}$
$=-f_{1}^{たて}e_{1}+f_{1}^{よこ}d_{1}
+f_{2}^{たて}e_{2}-f_{2}^{よこ}d_{2}
-f_{3}^{たて}e_{3}+f_{3}^{よこ}d_{3}$
となる。
$\Sigma_{Q}$ は点$Q$を中心に左回りを正として、
点$Q$回りのモーメントをすべて足し算するという意味である。
モーメントの向きを(画面を見ている人から見て)左回りにしたのは、
右手系の
$x$軸(画面を飛び出す向き)の右ねじまわりと一応は一致させておこうと思ったから。
右手系では、モーメントは座標軸の右ねじまわりで定義されるのが
一般的である(3次元の$x,y,z$軸回りの3つのモーメント
$M_{x}, M_{y}, M_{z}$のうち、
二次元で表現できるのは、
画面に垂直な$x$軸回りのモーメント$M_{x}$だけ)。
仮に平面座標に$x,y$座標を用いた場合、
$x$が右向き正で、$y$が上向き正の(中学、高校まででは)一般的な
表記なら、
右手系の
$z$軸は画面を飛び出す向きになるから、
右ねじ回りの$M_{z}$は画面を見ている人にとっては反時計回りになる。
構造力学などで、$x$は右向き正だけど$y$は下向き正みたいな座標を
使うと、右手系の$z$は画面の中へ突き進む方向になるので、
右ねじ回りの$M_{z}$は画面を見ている人にとっては時計回りになる。
但し、構造力学で用いられる断面力としてのモーメントの向きは、
後で詳しく述べるように
右手系の向きとは関係ない(梁の曲がるの向きに関係する)ので留意すること。
は点$Q$を中心に左回りを正として、
点$Q$回りのモーメントをすべて足し算するという意味である。
モーメントの向きを(画面を見ている人から見て)左回りにしたのは、
右手系の
$x$軸(画面を飛び出す向き)の右ねじまわりと一応は一致させておこうと思ったから。
右手系では、モーメントは座標軸の右ねじまわりで定義されるのが
一般的である(3次元の$x,y,z$軸回りの3つのモーメント
$M_{x}, M_{y}, M_{z}$のうち、
二次元で表現できるのは、
画面に垂直な$x$軸回りのモーメント$M_{x}$だけ)。
仮に平面座標に$x,y$座標を用いた場合、
$x$が右向き正で、$y$が上向き正の(中学、高校まででは)一般的な
表記なら、
右手系の
$z$軸は画面を飛び出す向きになるから、
右ねじ回りの$M_{z}$は画面を見ている人にとっては反時計回りになる。
構造力学などで、$x$は右向き正だけど$y$は下向き正みたいな座標を
使うと、右手系の$z$は画面の中へ突き進む方向になるので、
右ねじ回りの$M_{z}$は画面を見ている人にとっては時計回りになる。
但し、構造力学で用いられる断面力としてのモーメントの向きは、
後で詳しく述べるように
右手系の向きとは関係ない(梁の曲がるの向きに関係する)ので留意すること。
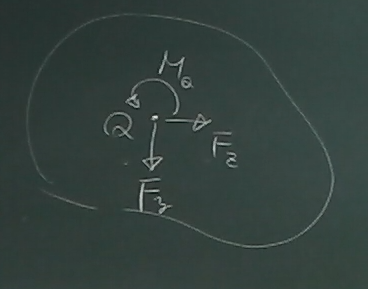 以上より、
$f_{1}, f_{2}, f_{3}$
を$Q$点に作用する
$y$方向の力、$z$方向の力、左回りのモーメントに置き換えてみると、
図のようになる。
但し、
以上より、
$f_{1}, f_{2}, f_{3}$
を$Q$点に作用する
$y$方向の力、$z$方向の力、左回りのモーメントに置き換えてみると、
図のようになる。
但し、
$F_{y}=(-f_{1}^{たて})+(-f_{2}^{たて})+(+f_{3}^{たて})$
$F_{z}=(-f_{1}^{よこ})+(+f_{2}^{よこ})+(+f_{3}^{よこ})$
$M_{Q}=-f_{1}^{たて}e_{1}+f_{1}^{よこ}d_{1}
+f_{2}^{たて}e_{2}-f_{2}^{よこ}d_{2}
-f_{3}^{たて}e_{3}+f_{3}^{よこ}d_{3}$
上記の問題で、物体が静止している場合、そのまま静止し続ける
(並進移動も回転移動も開始しない)条件は、
物体に作用している外力の合計がゼロになることである。
これは、物体に力が作用しなければ物体は加速度を持たないという
慣性の法則と捉えることもできるし、
$F=ma$の運動の法則で加速度$a$が0と捉えることもできる
(厳密にはこれら2つの法則の両方を必要とする結果と
解釈すべき
かも知れない
が、構造力学ではこの辺の厳密な
解釈は特に問題にはならない)。
もちろん、力が加わらない物体でも等速度運動なら可能である。
構造力学で扱うつりあいの問題は、静止している物体がそのまま静止し
続けるような問題であり、静力学と呼ばれる。
すなわち、
2次元の問題では、
鉛直方向に静止し続ける条件: 鉛直方向の力の合計がゼロ
水平方向に静止し続ける条件: 水平方向の力の合計がゼロ
回転に対して静止し続ける条件: 任意の点についてのモーメントの合計がゼロ
の3つの条件が成り立っているとき、「つりあっている」という。
これを上記の問題について具体的に書けば以下のようになる。
鉛直方向に静止し続ける条件: $F_{y}=(-f_{1}^{たて})+(-f_{2}^{たて})+(+f_{3}^{たて})=0$
水平方向に静止し続ける条件: $F_{z}=(-f_{1}^{よこ})+(+f_{2}^{よこ})+(+f_{3}^{よこ})=0$
回転に対し静止し続ける条件: $M_{Q}=-f_{1}^{たて}e_{1}+f_{1}^{よこ}d_{1}
+f_{2}^{たて}e_{2}-f_{2}^{よこ}d_{2}
-f_{3}^{たて}e_{3}+f_{3}^{よこ}d_{3}=0$
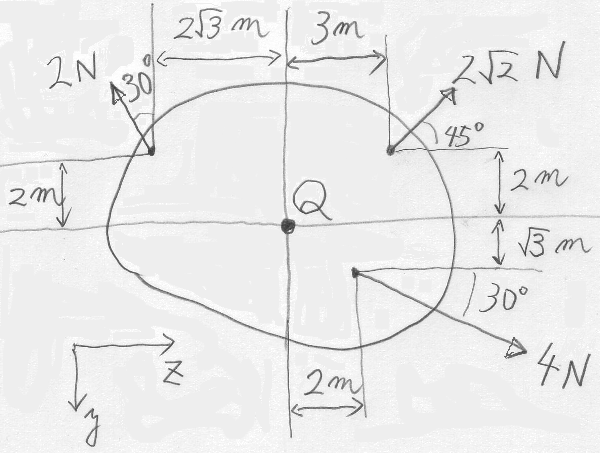 図のような物体(剛体)に作用する3つの力を
$Q$点に作用する
$y$方向の力、$z$方向の力、左回りのモーメントに置き換えてみよう。
図のような物体(剛体)に作用する3つの力を
$Q$点に作用する
$y$方向の力、$z$方向の力、左回りのモーメントに置き換えてみよう。
答えつきの問題の例は、
これ
(解答)とか
これ
(解答)とか。
2020年度小テスト第1回:
問1,
問2,
問3,
解答 。