服部の卒論日誌の履歴(No.30)

卒論テーマ†

CLT床版用の防護柵の開発（安部さんサポート）旭川の実験モデルをSalome-Mecaで再現（小川さんの修論や安部さんの卒論のモデル化）。

2つに割れている鞘管が1つずつ順番に降伏することで、どれぐらいエネルギーを吸収できているかを評価。

https://www.str.ce.akita-u.ac.jp/~gotouhan/j2023/hattori23/防護柵支柱試験_2024.odg

↑防護柵　図面

・小川さんの論文　CLT床版への取付・交換を考慮した鋼製防護柵の破壊挙動，構造工学論文集，Vol. 70A, p. 885-893, 2024/3. https://doi.org/10.11532/structcivil.70A.885

・小川さん卒論：CLT床版に取り付けられた鋼製防護柵の性能評価（概要　https://www.str.ce.akita-u.ac.jp/kouzou/pdf/so20og.pdf、スライド　https://www.str.ce.akita-u.ac.jp/kouzou/pdf/so20ogp.pdf）

・小川さん修論：CLT 床版への取付・交換が容易な鋼製防護柵の破壊挙動（スライド　https://www.str.ce.akita-u.ac.jp/kouzou/pas/sy22ogp.pdf）

・安部さん：支柱交換を考慮したCLT床版用鋼製防護柵の挙動（概要　https://www.str.ce.akita-u.ac.jp/kouzou/pas/so22ab.pdf、スライド　https://www.str.ce.akita-u.ac.jp/kouzou/pas/so22abp.pdf）

↑

4年次　進捗†

↑

24/6/~18†

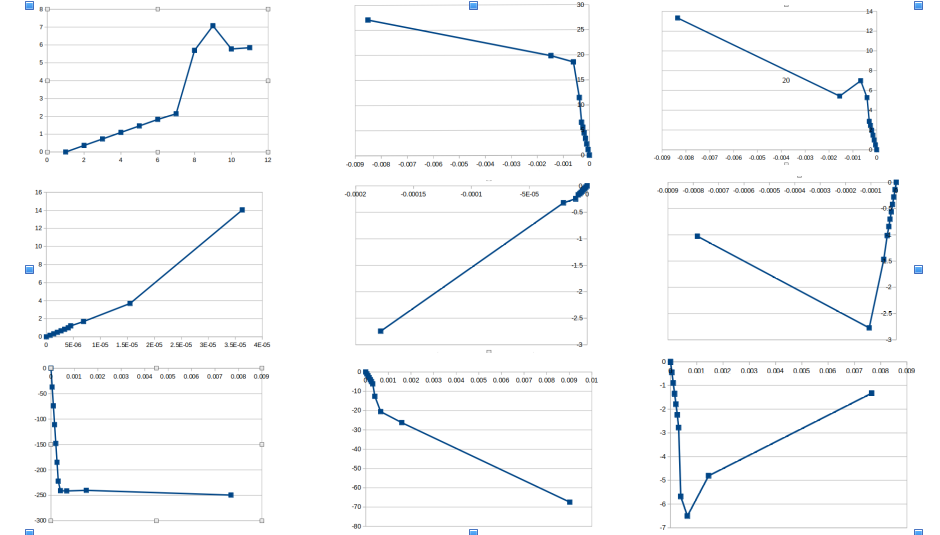
左のグラフが過去の実験結果を示したグラフで右が解析結果によるグラフ。

仮想材料を用いても降伏が一回しか見られないという小川さんの結果を確認することができた。

↑

24/6/~11†

前回までのモデルで相当応力−相当ひずみ曲線を作成した。上のモデル図はSIEQ_NOEUのミーゼス応力を表示しｘが0.01の箇所（固定面側）でスライスしたもの。

前回の応力−ひずみ曲線はマイナスの値を取っていたり、与えていたはずの応力よりも圧倒的に早く降伏してしまっていた。改善のためまずマイナスでなくなるように絶対値を用いる相当応力と相当ひずみを使用することになった。

Paravisで相当ひずみを確認するためにAsterStudyで設定を付け加える必要があった。まずPost ProcessingのCLAC_CPAMPよりCRUTERES（基準値）のところで以前はSIEQ_NOEU（相当応力）のみだったが、ここにEPEQ_NOEU（相当ひずみ）を加えた。そしてOutputも同様にEPEQ_NOEUを加えることでParavis で相当ひずみを確認することができるようになる。

相当応力−相当ひずみ曲線を作成した際、スライスした箇所は固定面側の面をスライスしたがｘが０の箇所ではスライスができないためｘが0.01の箇所でスライスした。前回は断面の９箇所のグラフを作成していたが、今回はスライスした断面の上部と下部の中央の点の２箇所のみとして（それ以外はあまり意味がないため）２つのグラフを作成した。結果としてしっかり設定荷重（238MPa）で降伏するグラフを得ることができた。

卒論に関しては、以前までは「Atype」と「Btype」と書かれていた過去の似た内容の卒論をしていた小川さんのデータを参考にさせてもらってモデルを作成しようとしていたが、今回の新しいモデルで必要だった内鞘に関する情報がないモデルで設計図にも内鞘のサイズなどに関する情報がなかったため、そこで止まってしまっていたが、先日「Ctype」という内鞘の使用されているモデルのデータを見つけてもらったため、まずこのモデルを自分の使用しているパソコンで解析が回るかを試し、内鞘が2段階に降伏するため応力−ひずみ曲線は二段階に降伏するものが得られるはずだからその確認をしてみようとなった。

当然であったが15分程度では解析が回らず、設定時間が足りないというエラーが出てしまったので45分で試したが同様のエラーが出てしまったため、10時間に設定し次の日に確認しようとしたがデータが飛んでしまっていたため、もう一度解析を回して、明日確認し続きを行ってみようと考えている。

↑

24/5/30†

https://www.str.ce.akita-u.ac.jp/~gotouhan/j2023/hattori23/応力para.png

上記の写真が今回使用した片持ちばりの載荷されている様子の写真で、このモデルの最もひずみが見られる箇所をスライスしてプロットした点から作った応力−ひずみ曲線が上記のグラフのようになった。

応力がマイナスになっているのは圧縮、プラスになっているのは引張が働いているからだと思われる。paravisの設定をミーゼス応力で見ると応力が絶対値で見ることができる（ミーゼス応力はスカラー量であり、応力の方向を示さないため）。

↑

24/5/22~28†

先週作っていたモデルをecro_lineを用いた設定の仕方でも作成してみた。弾塑性解析で作ったモデルをParavisで設定する方法等を練習。載荷面の9箇所等、特定のポイントそれぞれの応力−ひずみ曲線のグラフを作成するためにPlot Selection Over timeを用いた設定方法を覚えた。小川さんのモデルをParavisで見る時、どのように応用できるか知るために行ってきたが、設定を理解するのにかなり時間がかかってしまったため（というかまだしっかりは理解しきれていない）まだtimeの数値を変えたもののグラフを作成したりはできていないため行ってみる。また、後藤先生に送ってもらった新しいモデルの図面は限界まで拡大したら蛍光色で書かれていた文字も読むことができた。

これは載荷面の右上端の点のものだが、上記のようなグラフになってしまった。今回、特に理由はなく載荷面をスライスしていたため、ひずみの最も変化のある箇所をスライスしてみてやったら、というアドバイスをもらったから試してみる。

↑

24/5/16～21†

・やったこと

小川さんの卒論のスライドや概要の内容を読んだ。そして卒論などで使っていたと思われるサロメのデータを使わせてもらって、自分の使っているパソコンで解析が回るかの確認。解析は回ったが、弾塑性の内容についてよくわかっていなかったため、とりあえず弾塑性の春課題にあった簡単な形状の100×20×10のモデルを設定の仕方などの確認の意味もこめて作成して解析を回してみた。

salome-meca 弾塑性解析（2021)

https://www.str.ce.akita-u.ac.jp/cgi-bin/pukiwiki/?cmd=read&page=Salome-Meca%E6%BC%94%E7%BF%92_%E5%BC%BE%E5%A1%91%E6%80%A7%E8%A7%A3%E6%9E%90%282021%29&word=%E5%BC%BE%E5%A1%91%E6%80%A7

↑

24/5/15(水）†

C種について

https://www.mlit.go.jp/notice/noticedata/sgml/070/79000132/ref/y0000002.pdf

↑

春課題について†

↑

24/5/1（水）†

メモ

・10*5*700 単純1次

鉛直1次理論値　37.15451

メッシュ	要素数	解析値	相対誤差
0.7	604706	37.8469	1.864
1	150957	39.3168	5.820
2	21270	47.7953	28.639
4	2609	75.567	103.386

鉛直2次　理論値　120.3942

メッシュ	要素数	解析値	相対誤差
0.7	604706	122.609	1.840
1	150957	127.365	5.790
2	21270	154.866	28.632
4	2609	244.558	103.131

鉛直3次　理論値　251.1547

メッシュ	要素数	解析値	相対誤差
0.7	604706	255.685	-1.804
1	150957	265.629	-5.763
2	21270	322.8	28.526
4	2609	509.496	102.861

水平1次　理論値　74.30902

メッシュ	要素数	解析値	相対誤差
0.7	604706	74.1075	0.271
1	150957	74.9296	0.835
2	21270	77.9669	4.923
4	2609	87.7007	18.022

水平2次　理論値　240.7885

メッシュ	要素数	解析値	相対誤差
0.7	604706	239.837	0.395
1	150957	242.486	0.705
2	21270	252.306	4.783
4	2609	283.626	17.791

水平3次　理論値　502.3093

メッシュ	要素数	解析値	相対誤差
0.7	604706	499.386	0.582
1	150957	504.892	0.514
2	21270	525.213	4.560
4	2609	590.132	17.484

↑

24/4/16(火)†

共振周波数解析について

https://www.muratasoftware.com/fwp/wp-content/uploads/2019/05/190507_%E7%89%87%E6%8C%81%E3%81%A1%E6%A2%81%E3%81%AE%E5%85%B1%E6%8C%AF%E5%91%A8%E6%B3%A2%E6%95%B0.pdf

振動設計について

https://www.fml.t.u-tokyo.ac.jp/lecture/handout/DE/yurenu/2019vibra1.pdf

↑

24/4/15(月）†

メモ

・Texで図を挿入する際に一段に2つ以上横に並べて図を貼る方法

   \begin{figure}[h]
 　 \begin{tabular}{cc}
     %---- 最初の図 ---------------------------
     \begin{minipage}{0.45\hsize}
       \begin{center}
       \includegraphics[width=サイズ]{ファイル1}
       \caption{キャプション1}
       \label{ラベル1}
     \end{minipage} &
     %---- 2番目の図 --------------------------
     \begin{minipage}{0.45\hsize}
       \centering
       \includegraphics[width=サイズ]{ファイル2}
       \caption{キャプション2}
       \label{ラベル2}
     \end{minipage}
     %---- 図はここまで ----------------------
   \end{tabular}
 \end{figure}

図がかぶってしまうときは[width]のサイズを変えたりする。

今回は2つを横に並べただけで試していないがおそらく\begin{tabular}{cc}のccの数を増やすことで並べる図の数を変更できると思う。

参考文献

http://www.yamamo10.jp/~yamamoto/comp/latex/make_doc/insert_fig/index.php

・texで表を作成した際に全体のサイズを変更する方法

→\scalebox で拡大・縮小する

\begin{table}[htbp]
 \begin{center}
 \caption{表題}
 \label{heading}
 \scalebox{0.5}[0.9]{ %ココ
  \begin{tabular}{|c|c|c|c|} \hline
    & & & \\\hline 
    & & & \\\hline
  \end{tabular}
   }
 \end{center}
\end{table}

通常のグラフを作成して\label{heading}の後に\scalebox{0.5}[0.9]{　を入れ、\end{tabular}の後、｝で閉じる。

\scaleboxの後ろの｛｝で横倍率、[]で縦倍率が変更可能。ただ、[]は省略可能で、今回は｛｝のみで試したがうまく行った。

参考文献

https://blog.goo.ne.jp/shafact/e/8219383eb299d5b6bdfd1544d546df9f

・texでの矩形選択とコピペ方法

Escを押した後、Ctrl＋vで矩形選択モードになり矢印キーで選択。

選択したい箇所が決まったら、ｙでコピー。

その後、ｐで貼り付けるが、この時下の列に注意。貼り付ける時、挿入箇所から縦に無理やり挿入されるから、下に文章があるとその文章に割り込んだ形になるため、事前にスペースキーなどで列を揃えておく必要がある。

表を作成する際、メモを開いて

%\begin{figure}[h] ←これはいらない
%1 & \\
%2 & \\
%3 & \\
%4 & \\
%5 & \\
%6 & \\
%7 & \\
%8 & \\
%9 & \\
%1 & \\

的なものを用意してtexに作成する表のしたに貼り付けておくとかなり便利でした。

他にも表を多用する際は一度メモに使用するコマンドを貼り付けておき、そこからコピペすることでかなり時短になりました。ただ、これでも大量に表を作成すると時間はかかります。他にいい方法があるか今後探してみます。というかスクショを使えるときは絶対その方が楽です。

↑

創造工房実習 (3年次）†

↑

23/12/14(金)†

texの基本的な書き方https://www.str.ce.akita-u.ac.jp/~gotou/linux/gotouimes.txt参照

↑

23/12/08(金)†

メッシュの長さ	要素数	先端変位[mm]	相対誤差	計算者
0.7	155192	0.08378905246	15.365	安藤
0.8	138808	0.08380386491	15.350	安藤
0.9	82587	0.083707073981	15.45	兼田
1.1	38671	0.084201207602	14.95	兼田
1.2	31929	0.083688	15.466.	柴田
1.3	28621	0.083669	15.4857	柴田
1.4	28854	0.08368	15.47	佐藤
1.5	20015	0.084052	15.10	佐藤
1.6	19448	0.0835402938	15.62	皆川
1.7	13801	0.0834355098	15.72	皆川
1.8	12528	0.083733	15.42	永山
1.9	11769	0.083924	15.23	永山
2	10699	0.084076876559	15.074	辻
3	3579	0.08414561753	15.004	辻
4	1628	0.082794	16.37	服部
5	1016	0.083033	18.89	服部
6	839	-0.082882	16.26	梶原
7	554	-0.080871	18.28	梶原
8	285	0.079995	-19.20	工藤
9	261	0.078980	-20.22	工藤
10	232	0.081911	17.26	佐々木
11	208	0.075676	23.56	佐々木

↑

23/11/29(金）†

異方性１次について

自分のデータ

メッシュ長さ	要素数	変位	相対誤差	計算者
4	1500	0.430156	12.52	服部
5	432	0.282968	42.45	服部

全員のデータ

メッシュ長さ	要素数	先端変位	相対誤差	計算者
0.7	144563	0.505252	2.76	安藤
0.8	141517	0.504692	2.64	安藤
0.9	91648	0.502595	2.216	兼田
1.1	27160	0.489914	0.363	兼田
1.2	24675	0.487088	0.791	柴田
1.3	23446	0.4868010	0.995	柴田
1.4	17738	0.485999	1.16	佐藤
1.5	15438	0.485180	1.33	佐藤
1.6	15900	0.483286	1.71	皆川
1.7	12142	0.477952	2.80	皆川
1.8	11604	0.482085	1.9554	永山
1.9	10391	0.470887	4.2329	永山
2	10291	0.480910	2.19	辻
3	2328	0.431937	12.15	辻
4	1500	0.430156	12.52	服部
5	432	0.282968	42.45	服部
6	356	0.3441556	30.00	梶原
7	196	0.213934	56.49	梶原
8	104	0.229874	53.25	工藤
9	81	0.232308	52.75	工藤
10	78	0.203271	58.65	佐々木
11	63	0.222316	54.78	佐々木

等方性２次について

自分のデータ

メッシュ長さ	要素数	変位	相対誤差	計算者
4	1500	0.429254	3.01	服部
5	432	0.428170	2.75	服部

全員のデータ

メッシュ長さ	要素数	先端変位	相対誤差	計算者
0.7	144563	0.430124	3.22	安藤
0.8	141517	0.430132	3.22	安藤
0.9	91648	0.430020	3.197	兼田
1.1	27160	0.429828	3.151	兼田
1.2	24675	0.429836	3.15	柴田
1.3	23446	0.42974	3.13	柴田
1.4	17738	0.429797	1.3	佐藤
1.5	15438	0.429958	3.14	佐藤
1.6	15900	0.429755	3.18	皆川
1.7	12142	0.429676	3.11	皆川
1.8	11604	0.429829	3.1507	永山
1.9	10391	0.429684	3.1159	永山
2	10291	0.429620	3.10	辻
3	2328	0.429169	2.99	辻
4	1500	0.429254	3.01	服部
5	432	0.428170	2.75	服部
6	356	0.428452	2.82	梶原
7	196	0.42591	2.21	梶原
8	104	0.426074	2.25	工藤
9	81	0.425552	2.12	工藤
10	78	0.488382	17.20	佐々木
11	63	0.423972	9.0534	佐々木

↑

23/11/24(金）†

メッシュ長さ	要素数	先端変位	相対誤差	計算者
0.7	1455234	0.422484	1.388	安藤
0.8	142973	0.422570	1.409	安藤
0.9	91648	-0.420437	0.897	兼田
1.1	27160	-0.405618	2.659	兼田
1.2	24675	0.404349	2.96	柴田
1.3	23446	0.404185	3.00	柴田
1.4	17738	0.398604	4.34	佐藤
1.5	15438	0.396593	4.83	佐藤
1.6	16122	0.398212	4.44	皆川
1.7	12026	0.393411	5.59	皆川
1.8	11604	0.393668	5.53	永山
1.9	10391	0.390695	6.24	永山
2	10921	-0.395103	5.18	辻
3	2328	-0.324762	22.06	辻
4	1500	-0.155013	62.80	服部
5	432	-0.065278	84.33	服部
6	357	0.213062	48.87	梶原
7	196	0.1019	75.55	梶原
8	104	0.1158624	72.20	工藤
9	81	0.1255118	69.88	工藤
10	78	-0.07733	81.44	佐々木
11	63	-0.1999	52.03	佐々木

↑

23/11/17(金)†

すいません、僕のデータの相対誤差が100倍し忘れていたので直してあります。

メッシュ長さ	要素数	先端変位(4隅の平均値)[mm]	相対誤差	計算者
0.7	198464	6.54281	-1.91	安藤
0.8	113812	6.5104	-2.39	安藤
0.9	40280	6.3631525	-4.60	兼田
1.1	30055	6.3363525	-5.00	兼田
1.2	264667	6.3043375	5.48	柴田
1.3	25180	6.304355	5.48	柴田
1.4	32212	6.31612	5.31	佐藤
1.5	17753	6.1209	8.23	佐藤
1.6	14296	6.2044625	-6.98	皆川
1.7	13596	6.2156625	-6.81	皆川
1.8	2866	5.737755	-13.98	永山
1.9	6001	5.7263625	-14.15	永山
2	5617	5.6458525	-15.355	辻
3	2309	5.4728755	-17.948	辻
4	617	3.6160575	45.12	服部
5	494	3.8580375	42.16	服部
6	581	2.50682	-62.416	梶原
7	133	1.41225	-78.82	梶原
8	78	1.2887175	-80.68	工藤
9	72	1.2879925	-80.69	工藤
10	60	1.14344	-82.85	佐々木
11	65	1.23124	-81.154	佐々木

↑

23/11/10(金)†

↑

23/10/27(金)　コマンドと操作確認†

pwd : 自分の位置

ls : すべてのファイルを確認する

mkdir : 新規ファイルの作成　ls (作成できているかの確認）

cd ファイル名　：複数のファイルから特定のファイルに入る　pwd (現在位置の確認）

ls -a : 隠しファイル

gedit　ファイル名.tex & : ファイルを作りそのファイルに入るorもともとあるファイルに入る

vi ファイル名.tex : 編集（作業スペースからファイル内容を）　Esc →　: →　wq : 内容保存

cp コピーしたいファイル名　新しいファイル名.tex : 新しいファイルに違うファイルの内容をコピー）

rm ファイル名.tex : ファイルを消す

cd .. : 1つ前のフォルダに戻る（他ファイルの選択が可能に）

rmdir ファイル名　　：mkdirで作ったものの削除

マウスの両クリックor中央クリック　：　選択した文章コピーand貼り付け

↑

salome-meca 説明　†

http://dugi6514.odns.fr/doc/v15/en/index.php?man=commande

↑

salome-meca 設定に関する情報等†

https://www.slideshare.net/slideshow/salomemeca-59878666/59878666 https://qiita.com/Jun_Tatsuno/items/3e6558c1adc4dd9499fe

↑

メモ†

サロメの過去の人のデータをコピーする際はRun_Caseも一緒にコピーすると、Asterstudyの解析結果も確認することができる

服部の卒論日誌 の履歴(No.30)