![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
v
9/23,24 解析失敗. 固定条件や普及箇所の設定に間違いがあり,その部分の訂正も行った.
9/22 昨日から始めた解析は失敗。エラーの解決方法として、「CALC_MODES」において以前(5/11)変更した「PLUSS_PETTE」を「BANDE」に戻した。
9/21 解析失敗。材料定数の設定(field mat)は問題なさそう。固定条件の部分でちゃんと固定されていないかもしれないので、もう少し固定条件について調べてから回してみる。
9/20 解析失敗。材料の設定(field mat)の仕方を変え、固定条件を藤原さんのデータと同じにして解析を回してみる。
解析は何度か失敗し、引き続きエラーの修正をした。
9/18 何度か解析に失敗したが、明日の結果待ちの解析はこれまでのすぐにエラーがでた解析とは違い、長時間解析が行われている。
9/17 設定を一通り終え、解析を回してはみたが、失敗した。(多くのエラーがあり、一つ一つ取り除いている)
9/16 設定中にsalomeが重くなって作業がなかなか進まないため、原因の一つと考えられる要素数が多いことを解決するため次のことを行っていく。
・不必要なMeshの削除 ・アーチ以外(床板等)のMeshを粗くする。 ・それでもだめなら、吊り材の形を円柱から六角柱に変える。(軸方向・外側にとがっているところが向くように六角形のとがっているところがむくように)
9/15 今使用しているmeshの一部でより改良したmeshがありそちらを使うことにする。(9/12に見つけたaster studyのデータにはこちらのmeshが使われているため) 9/14 ・meshのグループ化の中で同じ名前のグループが存在しているため,名前を途中まで変更した.→meshに同じところを表しているところがあり、腐朽箇所に関係ない場所であったため、よりまとめて作られたmeshの方のみ残した。aster studyのfieldmatを進めた。
9/12 ・昨日グループ化し直したため、再度コンパウンドメッシュを行った。
・めおと橋の振動解析のAsters studyのデータらしきものが見つかったので先輩から頂いたデータと一緒に参考にしたい. ・Aster studyのedit textでできそうなところから進めた. ・meshのグループ化の中で同じ名前のグループが存在しているため,名前を途中まで変更した.
9/11 Asterstudyに挿入するテキストで別の橋でも振動解析なら共通のテキストと思われるものを挿入しようとしてもできなかった。アーチをグループ化した後にGeometryでcompoundしてから、meshを切ってもmeshのところではグループ化が反映されていなかったので,Geometryでcompoundせずに別々でmeshを切った。また,一部グループ化されていない部分があったので修正した。
9/9~10 Aster studyで不必要なテキストを消去した。また,挿入すべきテキストについてできるとこまで調べた。
9/8 Patitionしたアーチをグループ化し,分割した各領域に名前をつけた。
9/7 ・アーチの分割のための区切りの面の整理をした。 ・アーチのPartitionを行った。
(今は関係なかったが、Fuseをする際、立体と面をFuseすることはできないことが確認できた。立体と面をFuseしったい場合は面を厚さの薄い立体にすることでFuseできた。薄い立体にするには押し出しを使う。厚さは最少メッシュサイズの3倍~5倍くらいが安定するらしい。)
9/5 グループの作成やその前の準備(アーチの分割)を忘れていたので、そこから取り組む。アーチの分割のための区切りの面の作成まで行った。
9/4解析を回してみたが失敗。エラーの原因を調べ中
9/3中間発表の概論の作業を進めた。
9/2昨日行った現地調査(百目石橋、めおと橋)で撮影した写真をk2のファイルに上げた。
参考 ウォルトキング https://www.str.ce.akita-u.ac.jp/~gotouhan/j2023/aono/wiki/waltking.pdf 木材水分計 比重法 https://sooki.co.jp/upload/surveying_items/pdf/rel_pdf_file_1_054004.pdf
8/27 「Compound mesh」を行った。
8/23~26 「Compound mesh」を試したがやり方を間違えているためか上手く出来なかった。また、それ以外のsalome-mecaの使い方で忘れているところや分からないことを調べた。
8/22 近日中にやること Aster studyの設定→・アーチ部の局部座標系の設定(一旦異方性持たせない状態で解析回るか確認してから)・各部材ごとにmeshを切ったものをくっつける・その他数値の設定
8/5~8/21 Geometryを調べ直して,必要な部材の再確認を行った。また,各部材ごとにmeshを切った。
8/4 以前切られたと思われるMeshに含まれているGeometryについて調べたが、そのGeometryだけでは橋を構成するGeometryのすべてを満たしていない可能性があるため、Geometryについて調べ直す必要があるかもしれない。
7/31 ・めおと橋のアーチの上部と下部に面を作成をもう片方も行い、アーチ部のGeometry(腐食部の作成は除く)は完成した。 (腐食部の作成について腐食させる場所をつくったら番号つける。)
7/29 近日中にやること ・めおと橋のアーチの上部と下部に面を作成をもう片方も行う。 ・アーチ部のGeometryを完成させる。 ・部材ごと(アーチや床版など)のメッシュを切る。→Compound meshする。 ・アーチ部の局部座標系の設定を行う。
7/24 腐朽箇所が決定した。片方のアーチで「吊り材が6箇所、両端の支点で2箇所、中央の継手で1箇所の9箇所」だ(計18箇所).今後は、まずは腐朽せずに解析ができるか確認し、確認できたら1箇所のみ腐朽して固有振動数に変化があるか調べていく予定だ。
7/23 外国語文献発表(卒論について)
http://www.str.ce.akita-u.ac.jp/~gotouhan/j2024/kometani/7022548NaokiKometani.pdf
7/14 写真のようにめおと橋のアーチの上部と下部に面を作成することができた。これから座標や角度の設定を行っていきたい。
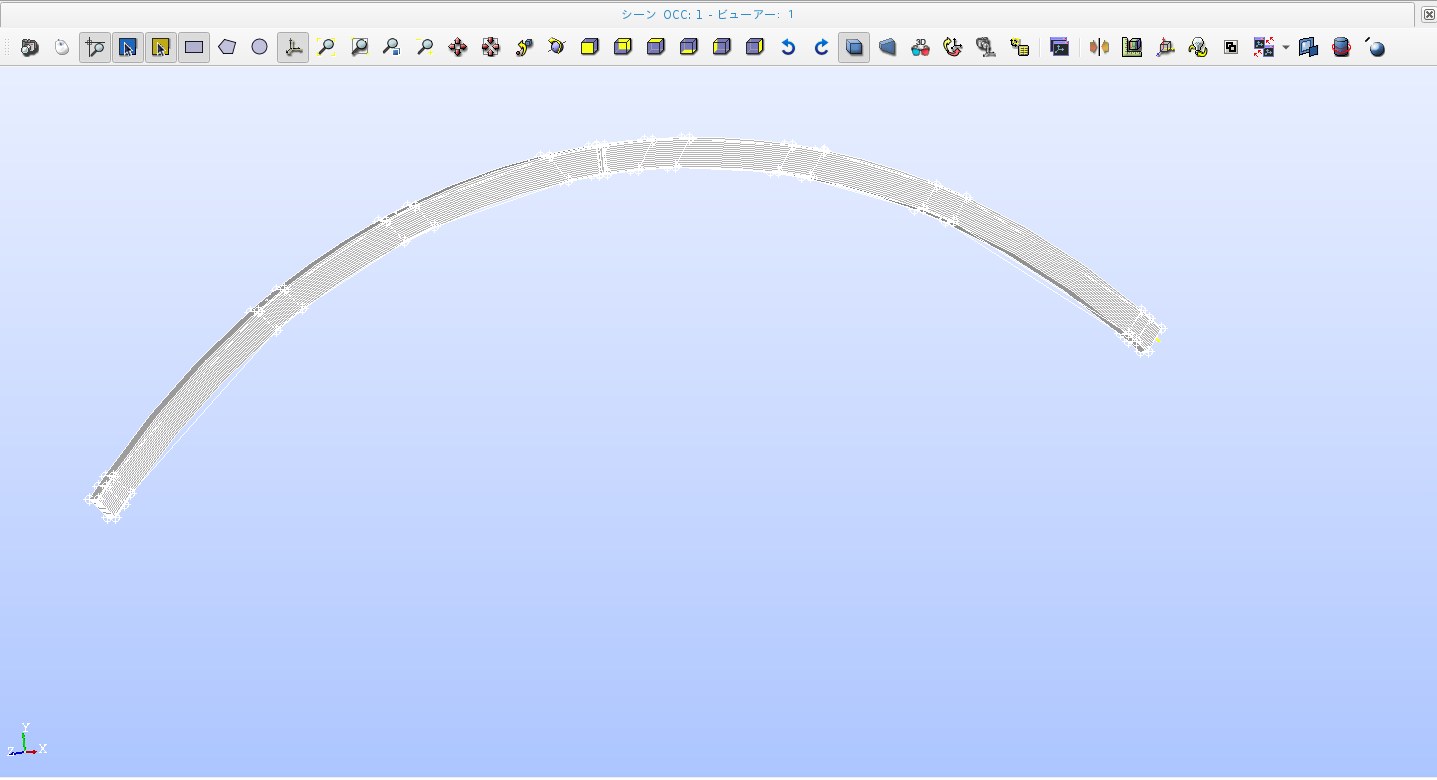
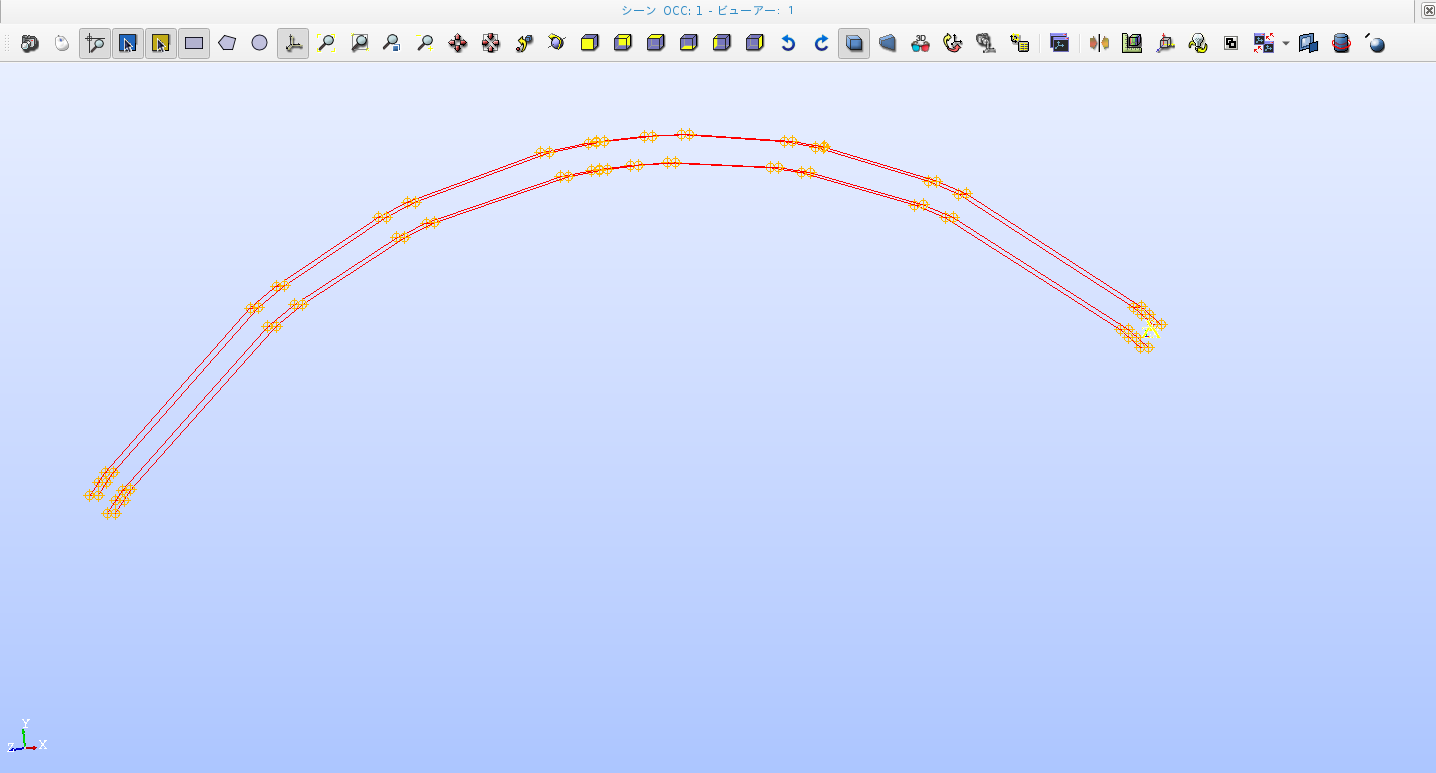 オイラー角参考
マニュアルのp.56. http://code-aster.org/doc/v12/en/man_u/u4/u4.42.01.pdf
オイラー角参考
マニュアルのp.56. http://code-aster.org/doc/v12/en/man_u/u4/u4.42.01.pdf
6/20 オイラー角参考ページ https://www.str.ce.akita-u.ac.jp/cgi-bin/pukiwiki/?cmd=read&page=Salome%E3%83%A1%E3%83%A2&word=%E3%82%AA%E3%82%A4%E3%83%A9%E3%83%BC%E8%A7%92#d473dc68 オイラー角とは? https://www.sky-engin.jp/blog/eulerian-angles/#toc2
6/18
http://www.str.ce.akita-u.ac.jp/~gotouhan/j2024/kometani/7022548米谷尚輝.pdf
オープンキャンパス 担当:振り子
参考ページ https://www.str.ce.akita-u.ac.jp/~gotouhan/j2015/kondo/opencampus/huriko.html, https://www.str.ce.akita-u.ac.jp/~gotou/souzou/pdf/huriko.pdf
6/11 Geometryの確認不足があり、すでにアーチがFuseされており、その上からPartatitionがされていた。それが同じ箇所に2回同じように行われていたので違いを考えたい。
6/10 ラミナは除く方針に決まった。そのため、アーチの分割されていた部分をFuseした。
6/9 モデルに入っているラミナが腐食(ヤング率の低下)に影響しているのかどうか考えたい。
5/29 メッシュを切った部材をくっつける作業をする際に参考となるファイルを頂いたので、それや右の参考ページを確認してやり方を学んでいく。 参考ページ https://www.str.ce.akita-u.ac.jp/cgi-bin/pukiwiki/?cmd=read&page=salome%20%E7%B5%90%E5%90%88%E3%83%A1%E3%83%A2&word=%E7%B5%90%E5%90%88%E3%83%A1%E3%83%A2#n02ca368
5/28 先輩のデータを見つけていただいた。また、メッシュを切る際に全てを切るのではなく部材ごとに分けてメッシュを切り、後からくっつける作業が必要だとわかった。
5/20~27 解析できない原因として、メッシュ長さがメッシュを切ることができない限界をこえている可能性があるため、メッシュ長さ10や0.9で試したができなかった。Geometryのデータが見当たらず、先輩のめおと橋のデータにもそのようなものがgFTPの中に見当たらなかった。必要なファイルがgFTPのどこにあるか聞く必要がある。
メッシュを作成する際、「NETGEN1D-2D-3D」、「サブメッシュを作成」が見当たらなかった。
5/19 メッシュ長さ2の解析を再度回せた。以前回したときと同じ結果だったので、メッシュ長さ1の時の解析を再度行ってみる。
5/18 16日と同様にエラーが起きた。原因かもしれないメッセージの表示があったので後日先輩に尋ねてみる。
5/16 解析にエラーが生じた。エラーメッセージでファイルやフォルダが存在しないと表示される。ファイル名やout putに誤りがあるかもしれないため、その辺りを変更して試してみる。
5/15 メッシュ長さ1と2の振動数解析値が同じになったので、再度解析を行い、誤りを見つける。
5/14
<About My Research>
Research Theme : Diagnosis of Deterioration of Timber Bridges by Vibration Analysis
How to reserch : I use Salonme-meca software to perform vibration analysis of a bridge model. (I got the model data of timber bridge from my senior.)

 Using model : MEOTO bridge (New bridge)
References : https://www.jstage.jst.go.jp/article/jscejj/79/7/79_22-00348/_pdf/-char/ja
Using model : MEOTO bridge (New bridge)
References : https://www.jstage.jst.go.jp/article/jscejj/79/7/79_22-00348/_pdf/-char/ja
MEOTO bridge is used in akita city
What I’m doing now : I perform vibration analysis with various number of elements and obtain convergence values.(I'm sorry.I'm having trouble with the analysis and don't have the results to show you yet.)
What to do in the future : I will perform a multiple regression analysis using the change in natural frequencies of multiple vibration modes as the explanatory variable and the change in Young's modulus at a specific decay point as the objective variable.
5/13 様々な要素数において解析し、収束値を求める。正しいかどうか先輩のデータを参考にさせていただく。参考データ: 様々な要素数において解析し、収束値を求める。
新めおと橋のデータのうち、かじか橋のデータを参考に変更した部分は次の部分です。
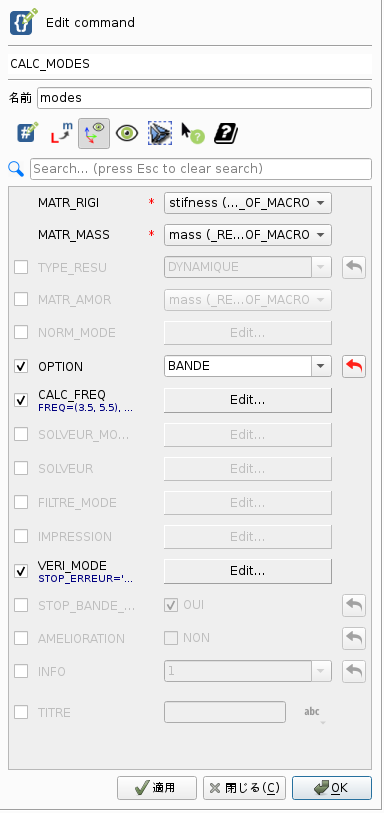
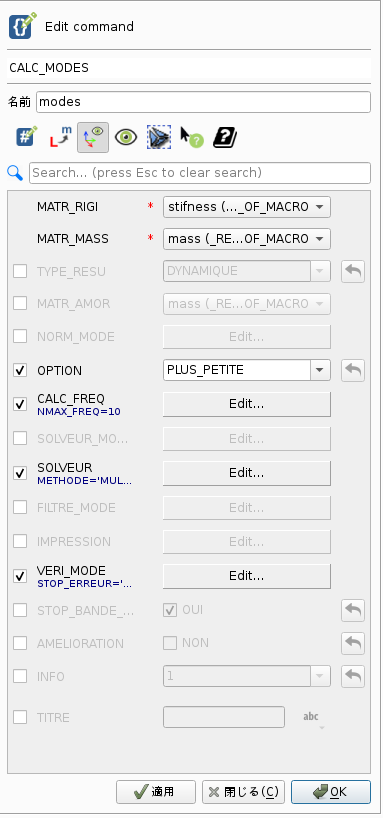 <左の写真> CALC_MODES (変更前),<右の写真> CALC_MODES (変更後)
<左の写真> CALC_MODES (変更前),<右の写真> CALC_MODES (変更後)
左の写真から右の写真に変更。変更点は次の通りです。OPTIONの「BANDE」→「PLUS_PETITE」。新たに「SOLVEUR」にチェック。
また、「CALC_FREQ」の詳細も変更しています。 「SOLVEUR」と「CALC_FREQ」の詳細については下記のようになります。
<左の写真> CALC_MODES > CALC_FREQ (変更前),<右の写真> CALC_MODES > CALC_FREQ (変更後)
左の写真から右の写真に変更。変更点は次の通りです。FREQを消去。NMAX_FREQを変更。
<写真> CALC_MODES > SOLVEUR (かじか橋の方にのみあった要素)
新たに「SOLVEUR」にチェックを入れ、上の写真のように設定した。
5/7 昨日行った解析が無事成功した。
5/6 5/3の解析は失敗。「CALC_MODES」と「ASSEMBLAGE」をかじか橋のデータに合わせて解析してみる。
5/3 メッシュ1,2,3で失敗。設定ミスがあるかもしれないので、再起動してから解析をやり直してみる。
5/2 全て1次要素にしたがエラーが生じたので、メッシュを変えてやってみる。まずは1.0で試す。
5/1 先輩のデータでは解析が成功した。新めおと橋を全て1次要素にして解析を行った。
4/30 Code_Asterについて https://code-aster.org/doc/v15/en/index.php?man=commande
先輩のかじか橋のデータを借りて、自分が使用しているパソコンで解析できるか確認する。
4/28 解析の確認と固定条件や材料定数の確認の続きをした。
4/26 解析が回していただきた結果を確認した。エラーメッセージが生じされていたので、原因を調べた。
4/25 新めおと橋に関するデータを頂いたので、解析が回るかの確認と固定条件や材料定数の確認を途中までした。 固定条件や材料定数を確認するときの参考:https://www.str.ce.akita-u.ac.jp/cgi-bin/pukiwiki/?salome-meca+%E5%85%A5%E9%96%80%E7%B7%A8%E3%80%80
4/24 対称木橋はめおと橋の新橋に決定した。 新めおと橋の解析をする前に、私が使用しているデスクトップパソコンで振動解析が回せるかどうか、他の橋のデータで試してみた。
4/23 卒論テーマの担当が決まった。私の担当するテーマは「局所的腐朽による木橋の固有振動数の感度の影響」だ。複数の振動モード(逆対称1次とか、水平対称1次とか、ねじり1次とか、それぞれの2次とか)の固有振動数の変化を説明変数にして、特定の腐朽箇所のヤング率の変化を目的変数にした重回帰分析をしていく。
対象木橋(予定):めおと橋
4/20~22 卒論テーマの担当決めを後藤班で話し合った。
4/19 後藤班が担当する卒論テーマについて、先輩方の日誌に目を通した。
4/17 デスクトップパソコンでSalome-mecaが問題なく使用できるかどうか確認した。
4/13
<10mm*10mm*150mm 1次要素>
水平1次~3次(1次要素) 10mm*10mm*150mm
| メッシュ長さ | 要素数 | 固有振動数解析値(水平1次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 2301.44 | 1.41995 |
| 0.8 | 135252 | 2301.84 | 1.40282 |
| 0.9 | 88820 | 2309.39 | 1.07942 |
| 1 | 85142 | 2316.73 | 0.76502 |
| 2 | 10828 | 2389.15 | 2.337027 |
| 3 | 2426 | 2603.3 | 11.50994 |
| 4 | 1076 | 2755.88 | 18.04557 |
| 5 | 662 | 2831.33 | 21.2774 |
| メッシュ長さ | 要素数 | 固有振動数解析値(水平2次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 6120.66 | 4.81474 |
| 0.8 | 135252 | 6122.25 | 4.79001 |
| 0.9 | 88820 | 6141.15 | 4.49609 |
| 1 | 85142 | 6160.52 | 4.19485 |
| 2 | 10828 | 6343.99 | 1.34163 |
| 3 | 2426 | 6881.19 | 7.012625 |
| 4 | 1076 | 7283.31 | 13.26618 |
| 5 | 662 | 7489.49 | 16.47258 |
| メッシュ長さ | 要素数 | 固有振動数解析値(水平3次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 11485.3 | 9.03633 |
| 0.8 | 135252 | 11488.4 | 9.01178 |
| 0.9 | 88820 | 11524 | 8.72983 |
| 1 | 85142 | 11559.7 | 8.44708 |
| 2 | 10828 | 11909.6 | 5.67587 |
| 3 | 2426 | 12860.3 | 1.853678 |
| 4 | 1076 | 13547.4 | 7.295515 |
| 5 | 662 | 13793.6 | 9.245421 |
鉛直1次~鉛直3次(1次要素) 10mm*10mm*150mm
| メッシュ長さ | 要素数 | 固有振動数解析値(鉛直1次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 2301.77 | 1.40581 |
| 0.8 | 135252 | 2302.39 | 1.37926 |
| 0.9 | 88820 | 2309.43 | 1.07771 |
| 1 | 85142 | 2316.81 | 0.76159 |
| 2 | 10828 | 2399.03 | 2.760228 |
| 3 | 2426 | 2652.94 | 13.63623 |
| 4 | 1076 | 2764.99 | 18.43579 |
| 5 | 662 | 2842.75 | 21.76656 |
| メッシュ長さ | 要素数 | 固有振動数解析値(鉛直2次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 6121.48 | 4.80198 |
| 0.8 | 135252 | 6123.75 | 4.76668 |
| 0.9 | 88820 | 6141.6 | 4.48909 |
| 1 | 85142 | 6161.53 | 4.17915 |
| 2 | 10828 | 6367.51 | 0.97585 |
| 3 | 2426 | 7000.16 | 8.862783 |
| 4 | 1076 | 7307.87 | 13.64813 |
| 5 | 662 | 7505.37 | 16.71954 |
| メッシュ長さ | 要素数 | 固有振動数解析値(鉛直3次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 11486.6 | 9.02604 |
| 0.8 | 135252 | 11490.8 | 8.99277 |
| 0.9 | 88820 | 11524.9 | 8.7227 |
| 1 | 85142 | 11561.1 | 8.436 |
| 2 | 10828 | 11948.6 | 5.36699 |
| 3 | 2426 | 13063.6 | 3.463815 |
| 4 | 1076 | 13617.1 | 7.84754 |
| 5 | 662 | 13932.5 | 10.34551 |
ねじれ1次、2次(1次要素) 10mm*10mm*150mm
| メッシュ長さ | 要素数 | 固有振動数解析値(ねじれ1次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 9921.31 | 29.4497 |
| 0.8 | 135252 | 9926.55 | 29.51807 |
| 0.9 | 88820 | 9988.02 | 30.32011 |
| 1 | 85142 | 10074.7 | 31.45108 |
| 2 | 10828 | 10682.4 | 39.38013 |
| 3 | 2426 | 12492.8 | 63.00158 |
| 4 | 1076 | 13028.7 | 69.99382 |
| 5 | 662 | 13932.5 | 81.78627 |
| メッシュ長さ | 要素数 | 固有振動数解析値(ねじれ2次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 17105.9 | 11.59583 |
| 0.8 | 135252 | 17106.7 | 11.60105 |
| 0.9 | 88820 | 17108.4 | 11.61214 |
| 1 | 85142 | 17104 | 11.58344 |
| 2 | 10828 | 17129.1 | 11.74718 |
| 3 | 2426 | 17159.8 | 11.94746 |
| 4 | 1076 | 17186.2 | 12.11969 |
| 5 | 662 | 17189.6 | 12.14187 |
<10mm*10mm*150mm 2次要素>
水平1次~3次(2次要素) 10mm*10mm*150mm
| メッシュ長さ | 要素数 | 固有振動数解析値(水平1次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 2280.6 | 2.31261 |
| 0.8 | 135252 | 2280.66 | 2.31004 |
| 0.9 | 88820 | 2280.77 | 2.30533 |
| 1 | 85142 | 2280.84 | 2.30233 |
| 2 | 10828 | 2282.1 | 2.24836 |
| 3 | 2426 | 2284.29 | 2.15455 |
| 4 | 1076 | 2286.66 | 2.05304 |
| 5 | 662 | 2289.02 | 1.95195 |
| メッシュ長さ | 要素数 | 固有振動数解析値(水平2次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 6065.03 | 5.67986 |
| 0.8 | 135252 | 6065.19 | 5.67738 |
| 0.9 | 88820 | 6065.48 | 5.67287 |
| 1 | 85142 | 6065.77 | 5.66836 |
| 2 | 10828 | 6069.13 | 5.6161 |
| 3 | 2426 | 6075.85 | 5.5116 |
| 4 | 1076 | 6083.26 | 5.39636 |
| 5 | 662 | 6091.63 | 5.26619 |
| メッシュ長さ | 要素数 | 固有振動数解析値(水平3次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 11381.4 | 9.85922 |
| 0.8 | 135252 | 11381.7 | 9.85685 |
| 0.9 | 88820 | 11382.2 | 9.85289 |
| 1 | 85142 | 11382.6 | 9.84972 |
| 2 | 10828 | 11389.2 | 9.79745 |
| 3 | 2426 | 11403.9 | 9.68102 |
| 4 | 1076 | 11420.2 | 9.55193 |
| 5 | 662 | 11440.2 | 9.39353 |
鉛直1次~鉛直3次(2次要素) 10mm*10mm*150mm
| メッシュ長さ | 要素数 | 固有振動数解析値(鉛直1次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 2280.61 | 2.31218 |
| 0.8 | 135252 | 2280.68 | 2.30918 |
| 0.9 | 88820 | 2280.78 | 2.3049 |
| 1 | 85142 | 2280.88 | 2.30062 |
| 2 | 10828 | 2282.23 | 2.24279 |
| 3 | 2426 | 2284.53 | 2.14427 |
| 4 | 1076 | 2287.09 | 2.03462 |
| 5 | 662 | 2289.38 | 1.93653 |
| メッシュ長さ | 要素数 | 固有振動数解析値(鉛直2次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 6065.05 | 5.67955 |
| 0.8 | 135252 | 6065.24 | 5.6766 |
| 0.9 | 88820 | 6065.5 | 5.67255 |
| 1 | 85142 | 6065.77 | 5.66836 |
| 2 | 10828 | 6069.52 | 5.61004 |
| 3 | 2426 | 6076.69 | 5.49853 |
| 4 | 1076 | 6084.62 | 5.37521 |
| 5 | 662 | 6092.46 | 5.25329 |
| メッシュ長さ | 要素数 | 固有振動数解析値(鉛直3次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 11381.4 | 9.85922 |
| 0.8 | 135252 | 11381.8 | 9.85605 |
| 0.9 | 88820 | 11382.3 | 22.9839 |
| 1 | 85142 | 11382.8 | 9.84813 |
| 2 | 10828 | 11390 | 9.79111 |
| 3 | 2426 | 11405.8 | 9.66597 |
| 4 | 1076 | 11423 | 9.52975 |
| 5 | 662 | 11447.7 | 9.33413 |
ねじれ1次、2次(2次要素) 10mm*10mm*150mm
| メッシュ長さ | 要素数 | 固有振動数解析値(ねじれ1次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 9723.73 | 26.87175 |
| 0.8 | 135252 | 9723.85 | 26.87332 |
| 0.9 | 88820 | 9724.24 | 26.8784 |
| 1 | 85142 | 9724.41 | 26.88062 |
| 2 | 10828 | 9734.46 | 27.01175 |
| 3 | 2426 | 9781.98 | 27.63177 |
| 4 | 1076 | 9922.74 | 29.46836 |
| 5 | 662 | 9984.68 | 30.27653 |
| メッシュ長さ | 要素数 | 固有振動数解析値(ねじれ2次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 147391 | 17097.5 | 11.54103 |
| 0.8 | 135252 | 17097.7 | 11.54234 |
| 0.9 | 88820 | 17098 | 11.54429 |
| 1 | 85142 | 17098.3 | 11.54625 |
| 2 | 10828 | 17102 | 11.57039 |
| 3 | 2426 | 17106 | 11.59648 |
| 4 | 1076 | 17113.2 | 11.64345 |
| 5 | 662 | 17115 | 11.6552 |
<10mm*10mm*300mm 1次要素>
水平1次~3次(1次要素) 10mm*10mm*300mm
| メッシュ長さ | 要素数 | 固有振動数解析値(水平1次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 586.326 | 0.458494 |
| 0.8 | 252556 | 586.465 | 0.48231 |
| 0.9 | 176621 | 588.027 | 0.749936 |
| 1 | 170307 | 587.992 | 0.743939 |
| 2 | 23085 | 607.145 | 4.025529 |
| 3 | 4685 | 665.92 | 14.09578 |
| 4 | 2102 | 689.902 | 18.20475 |
| 5 | 1404 | 678.16 | 16.19292 |
| メッシュ長さ | 要素数 | 固有振動数解析値(水平2次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 1600.72 | 0.42549 |
| 0.8 | 252556 | 1601.05 | 0.40496 |
| 0.9 | 176621 | 1605.24 | 0.14432 |
| 1 | 170307 | 1605.21 | 0.14618 |
| 2 | 23085 | 1656.92 | 3.070492 |
| 3 | 4685 | 1816.17 | 12.97681 |
| 4 | 2102 | 1885.18 | 17.26965 |
| 5 | 1404 | 1849.62 | 15.0576 |
| メッシュ長さ | 要素数 | 固有振動数解析値(水平3次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 3098.83 | 1.82889 |
| 0.8 | 252556 | 3099.48 | 1.8083 |
| 0.9 | 176621 | 3107.45 | 1.55581 |
| 1 | 170307 | 3107.21 | 1.56341 |
| 2 | 23085 | 3212.16 | 1.76141 |
| 3 | 4685 | 3505.98 | 11.06965 |
| 4 | 2102 | 3634.69 | 15.14719 |
| 5 | 1404 | 3572.79 | 13.18619 |
鉛直1次~3次(1次要素) 10mm*10mm*300mm
| メッシュ長さ | 要素数 | 固有振動数解析値(鉛直1次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 586.372 | 0.466375 |
| 0.8 | 252556 | 586.545 | 0.496016 |
| 0.9 | 176621 | 588.104 | 0.763129 |
| 1 | 170307 | 588.051 | 0.754048 |
| 2 | 23085 | 608.011 | 4.173906 |
| 3 | 4685 | 695.421 | 19.15035 |
| 4 | 2102 | 702.336 | 20.33513 |
| 5 | 1404 | 679.793 | 16.47271 |
| メッシュ長さ | 要素数 | 固有振動数解析値(鉛直2次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 1600.77 | 0.42238 |
| 0.8 | 252556 | 1601.32 | 0.38817 |
| 0.9 | 176621 | 1605.46 | 0.13063 |
| 1 | 170307 | 1605.49 | 0.12877 |
| 2 | 23085 | 1659.74 | 3.245913 |
| 3 | 4685 | 1894.5 | 17.84941 |
| 4 | 2102 | 1924.99 | 19.74607 |
| 5 | 1404 | 1855.56 | 15.42711 |
| メッシュ長さ | 要素数 | 固有振動数解析値(鉛直3次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 3099.04 | 1.82224 |
| 0.8 | 252556 | 3099.81 | 1.79784 |
| 0.9 | 176621 | 3107.84 | 1.54345 |
| 1 | 170307 | 3107.64 | 1.54979 |
| 2 | 23085 | 3217.09 | 1.917594 |
| 3 | 4685 | 3667 | 16.17077 |
| 4 | 2102 | 3700.35 | 17.2273 |
| 5 | 1404 | 3582.61 | 13.49729 |
ねじれ1次、2次(1次要素) 10mm*10mm*300mm
| メッシュ長さ | 要素数 | 固有振動数解析値(ねじれ1次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 4959.8 | 29.42739 |
| 0.8 | 252556 | 4962.54 | 29.49889 |
| 0.9 | 176621 | 4986.49 | 30.12387 |
| 1 | 170307 | 4985.57 | 30.09987 |
| 2 | 23085 | 5306.26 | 38.46836 |
| 3 | 4685 | 6321.06 | 64.94986 |
| 4 | 2102 | 6531.96 | 70.45335 |
| 5 | 1404 | 6289.02 | 64.11377 |
| メッシュ長さ | 要素数 | 固有振動数解析値(ねじれ2次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 8535.58 | 11.36919 |
| 0.8 | 252556 | 8535.78 | 11.3718 |
| 0.9 | 176621 | 8536.2 | 11.37728 |
| 1 | 170307 | 8536.53 | 11.38159 |
| 2 | 23085 | 8541.57 | 11.44735 |
| 3 | 4685 | 8549.11 | 11.54573 |
| 4 | 2102 | 8556.55 | 11.6428 |
| 5 | 1404 | 8556.24 | 11.63876 |
<10mm*10mm*300mm 2次要素>
水平1次~3次(2次要素) 10mm*10mm*300mm
| メッシュ長さ | 要素数 | 固有振動数解析値(水平1次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 581.061 | 0.44359 |
| 0.8 | 252556 | 581.07 | 0.44205 |
| 0.9 | 176621 | 581.085 | 0.43948 |
| 1 | 170307 | 581.097 | 0.43742 |
| 2 | 23085 | 581.246 | 0.41189 |
| 3 | 4685 | 581.52 | 0.36494 |
| 4 | 2102 | 581.839 | 0.31029 |
| 5 | 1404 | 582.04 | 0.27585 |
| メッシュ長さ | 要素数 | 固有振動数解析値(水平2次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 1586.31 | 1.32188 |
| 0.8 | 252556 | 1586.34 | 1.32001 |
| 0.9 | 176621 | 1586.38 | 1.31752 |
| 1 | 170307 | 1586.41 | 1.31566 |
| 2 | 23085 | 1586.83 | 1.28953 |
| 3 | 4685 | 1587.66 | 1.2379 |
| 4 | 2102 | 1588.62 | 1.17818 |
| 5 | 1404 | 1589.16 | 1.14459 |
| メッシュ長さ | 要素数 | 固有振動数解析値(水平3次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 3070.7 | 2.72005 |
| 0.8 | 252556 | 3070.75 | 2.71847 |
| 0.9 | 176621 | 3070.83 | 2.71593 |
| 1 | 170307 | 3070.89 | 2.71403 |
| 2 | 23085 | 3071.73 | 2.68742 |
| 3 | 4685 | 3073.52 | 2.63071 |
| 4 | 2102 | 3075.59 | 2.56513 |
| 5 | 1404 | 3076.7 | 2.52997 |
鉛直1次~3次(2次要素) 10mm*10mm*300mm
| メッシュ長さ | 要素数 | 固有振動数解析値(鉛直1次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 581.061 | 0.44359 |
| 0.8 | 252556 | 581.072 | 0.4417 |
| 0.9 | 176621 | 581.085 | 0.43948 |
| 1 | 170307 | 581.097 | 0.43742 |
| 2 | 23085 | 581.246 | 0.41189 |
| 3 | 4685 | 581.555 | 0.35895 |
| 4 | 2102 | 581.87 | 0.30498 |
| 5 | 1404 | 582.072 | 0.27037 |
| メッシュ長さ | 要素数 | 固有振動数解析値(鉛直2次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 1586.31 | 1.32188 |
| 0.8 | 252556 | 1586.34 | 1.32001 |
| 0.9 | 176621 | 1586.38 | 1.31752 |
| 1 | 170307 | 1586.41 | 1.31566 |
| 2 | 23085 | 1586.88 | 1.28642 |
| 3 | 4685 | 1587.76 | 1.23168 |
| 4 | 2102 | 1588.72 | 1.17196 |
| 5 | 1404 | 1589.26 | 1.13837 |
| メッシュ長さ | 要素数 | 固有振動数解析値(鉛直3次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 3070.7 | 2.72005 |
| 0.8 | 252556 | 3070.76 | 2.71815 |
| 0.9 | 176621 | 3070.83 | 2.71593 |
| 1 | 170307 | 3070.9 | 2.71371 |
| 2 | 23085 | 3071.84 | 2.68393 |
| 3 | 4685 | 3073.77 | 2.62279 |
| 4 | 2102 | 3075.84 | 2.55721 |
| 5 | 1404 | 3076.96 | 2.52173 |
ねじれ1次、2次(2次要素) 10mm*10mm*300mm
| メッシュ長さ | 要素数 | 固有振動数解析値(ねじれ1次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 4856.56 | 26.73331 |
| 0.8 | 252556 | 4856.61 | 26.73462 |
| 0.9 | 176621 | 4856.74 | 26.73801 |
| 1 | 170307 | 4856.83 | 26.74036 |
| 2 | 23085 | 4860.64 | 26.83978 |
| 3 | 4685 | 4882.43 | 27.4084 |
| 4 | 2102 | 4956.24 | 29.33449 |
| 5 | 1404 | 5016.28 | 30.90125 |
| メッシュ長さ | 要素数 | 固有振動数解析値(ねじれ2次) | 相対誤差(\( \frac{salome-手計算}{手計算} \)) |
| 0.7 | 274220 | 8533.55 | 11.34271 |
| 0.8 | 252556 | 8533.61 | 11.34349 |
| 0.9 | 176621 | 8533.69 | 11.34453 |
| 1 | 170307 | 8533.75 | 11.34532 |
| 2 | 23085 | 8534.65 | 11.35706 |
| 3 | 4685 | 8536.09 | 11.37585 |
| 4 | 2102 | 8537.66 | 11.39633 |
| 5 | 1404 | 8537.93 | 11.39986 |
解析がうまく行かなかった時の参考 https://forum.code-aster.org/public/
2/14春課題
2/12春課題
梁要素の片持ち梁の振動解析 https://www.youtube.com/watch?v=5SYHxrAr4f8)%E3%81%BE%E3%81%9A%E3%81%AF について Analysis,CALC_MODES,Optionではこのシェル要素のYoutubeで,「とりあえずPLUS_PETITEを選択しときましょう」みたいに言っており、とりあえずPLUS_PETITEを選択. Analysis,CALC_MODESのSolverとSTOP_BANDEとTYPE_RESUはぜんぶ消したのは上のシェル要素のYoutubeでこの項目がなかったから。 AnalysisのVERI_MODEをEditし,STOP_ERREURのチェックを外してNoにした
11/29 創造工房実習 Salome-Meca用いて単純梁を解き解き、中央断面の変位の平均を求めた。結果は図1のようになった。
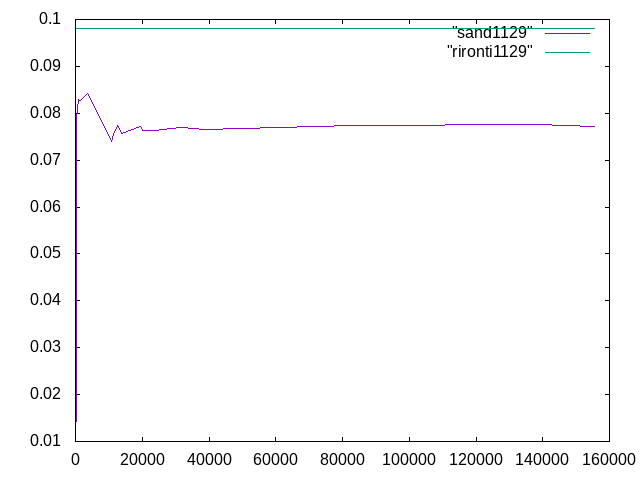
図1 サンドイッチ梁 中央断面の変位 (X軸: 要素数, Y軸: 中央断面の変位)
「rironti1129」のグラフはサンドイッチ梁の変位の中央断面の理論値を表している。今回は以下の条件で中央断面に荷重を加えた。
・サンドイッチ梁全体の長さ : 120(mm) ・ピン支点の位置 : 10 (mm) ・ローラー支点の位置 : 110 (mm) ・支点間距離: 100 (mm ) ・線荷重:10 (N/mm) ・中央断面にかかる荷重P : 10 (N/mm)×10(mm)=100(N) ・断面二次モーメントI : (10×10^3) / 12 (mm^4)
○鋼材(木材の上下に2箇所) ・ヤング率E:206000 (MPa) =206000 (N/mm^2)
・ポアソン比ν:0.3
・断面:1mm×10mm
・断面積A : 10mm^2
○木材 ・ヤング率E:6000 (MPa) =6000 (N/mm^2)
・ポアソン比ν:0.4
・断面:8mm×10mm
・断面積A : 80mm^2
・せん断補正係数k : 5/6
・せん断弾性係数G : 400
木材と鋼材を合わせたEIについて
EI= 6000×(10×8^3/12) + 2×206000×10×4.5^2 = 836860000
これらの条件より理論上の変位は次のようになる
PL^3/48EI + Pl/4kGA = (100×120^3) / (48×836860000) + (100×100×6)/ (4×5×400×80) (mm) = 0.004301794804 + 0.09375 = 0.0980517948 ≒ 0.098
「sand1129」のグラフはSalome-Meca用いて解いたサンドイッチ梁の中央断面の変位の平均(実験値)を表している。このグラフ作成に用いたデータは以下の表のとおりである。
| メッシュ長さ | 要素数 | 先端変位(4隅の平均値)[mm] | 相対誤差(\( \frac{salome-手計算}{手計算} \)) | 計算者 |
| 0.7 | 155419 | 0.0772 | 26.943 | 湊 |
| 0.8 | 138734 | 0.0775 | 26.452 | 湊 |
| 0.9 | 82935 | 0.0774 | 26.614 | 湊 |
| 1.1 | 38671 | 0.0766 | 27.937 | 森井 |
| 1.2 | 32044 | 0.0770 | 27.273 | 森井 |
| 1.3 | 28599 | 0.0768 | 27.604 | 森井 |
| 1.4 | 23950 | 0.07640 | 22.04 | 米谷 |
| 1.5 | 19998 | 0.07641 | 22.03 | 米谷 |
| 1.6 | 19448 | 0.07715 | 21.28 | 米谷 |
| 1.7 | 13801 | 0.07567 | 22.79 | 米谷 |
| 1.8 | 12677 | 0.07736 | 21.06 | 沼野 |
| 1.9 | 11464 | 0.07546 | 23.00 | 沼野 |
| 2 | 10699 | 0.07404 | 24.45 | 沼野 |
| 3 | 3579 | 0.08414 | 15.004 | 國井 |
| 4 | 1628 | 0.08279 | 16.37 | 國井 |
| 5 | 1016 | 0.08303 | 16.26 | 國井 |
| 6 | 839 | 0.08288 | 16.26 | 西澤 |
| 7 | 554 | 0.08087 | 18.28 | 西澤 |
| 8 | 285 | 0.07898 | 19.20 | 西澤 |
| 9 | 261 | 0.01421 | 85.49 | 真庭 |
| 10 | 232 | 0.03380 | 65.51 | 真庭 |
| 11 | 208 | 0.00913 | 90.68 | 真庭 |
11/22 創造工房実習 Salome-Meca用いて前回の単純梁を直交異方性や二次要素に条件を変更して解き、中央断面の変位の平均を求めた。結果は図1のようになった。
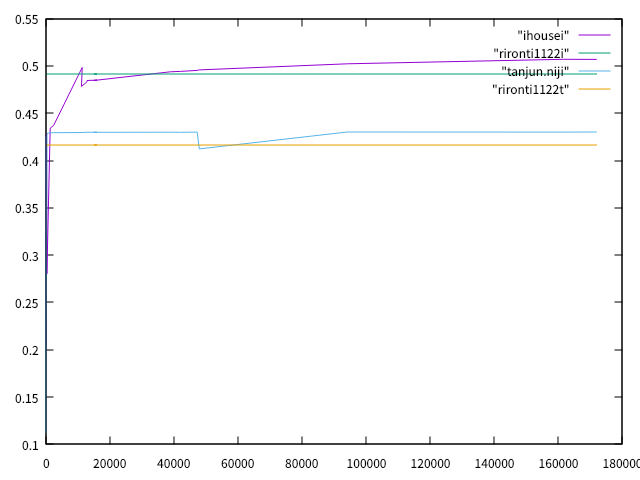
図1 単純梁 中央断面の変位 (X軸: 要素数, Y軸: 中央断面の変位)
「rironti1122i」のグラフは前回の単純梁を直交異方性にした時の中央断面の変位の理論値を表している。今回は以下のような条件で単純梁の中央に荷重を加えた。
・ヤング率E:6000 (MPa) =6000 (N/mm^2)
・ポアソン比ν:0.4
・単純梁全体の長さ : 120(mm)
・ピン支点の位置 : 10 (mm)
・ローラー支点の位置 : 110 (mm)
・支点間距離: 100 (mm )
・断面:10mm×10mm
・断面積A : 100mm^2
・線荷重:10 (N/mm)
・中央断面にかかる荷重P : 10 (N/mm)×10(mm)=100(N)
・断面二次モーメントI : (10×10^3) / 12 (mm^4)
・せん断補正係数k : 5/6
・せん断弾性係数G : 400
これらの条件より理論上の変位は次のようになる
PL^3/48EI + Pl/4kGA = (100×100^3×12) / (48×6000×10×10^3) + (100×100×6)/ (4×5×400×100) (mm) =0.4166666667 + 0.075 (mm) ≒ 0.4167 + 0.075 = 0.4917 (mm)
また、「rironti1122t」のグラフは前回の単純梁の二次要素(観測箇所を増やしている)における中央断面の変位の理論値を表している。そのため、理論値は前回と同様に0.4167程度となる。
続いて、Salome-Meca用いて解いた単純梁の中央断面の変位の平均(実験値)について、「ihousei」のグラフは直交異方性、「tanjun.niji」のグラフは二次要素においての変位の平均(実験値)である。このグラフ作成に用いたデータは以下の表のとおりである。
| メッシュ長さ | 要素数 | 変位(異方性)[mm] | 相対誤差-異方性(\( \frac{salome-手計算}{手計算} \)) | 変位(等方性)[mm] | 相対誤差-等方性(\( \frac{salome-手計算}{手計算} \)) | 計算者 |
| 0.7 | 171996 | 0.5068 | 2.993 | 0.4301 | 3.141 | 湊 |
| 0.8 | 161561 | 0.5069 | 2.999 | 0.4300 | 3.116 | 湊 |
| 0.9 | 94185 | 0.5021 | 2.071 | 0.4301 | 3.139 | 湊 |
| 1.1 | 47998 | 0.4957 | 0.814 | 0.4122 | 1.056 | 森井 |
| 1.2 | 47343 | 0.4952 | 0.712 | 0.4300 | 3.217 | 森井 |
| 1.3 | 42112 | 0.4941 | 0.488 | 0.4298 | 3.169 | 森井 |
| 1.4 | 38960 | 0.4937 | 0.407 | 0.4299 | 3.193 | 森井 |
| 1.5 | 15041 | 0.4845 | 1.460 | 0.4298 | 3.179 | 米谷 |
| 1.6 | 16071 | 0.4849 | 1.380 | 0.4298 | 3.157 | 米谷 |
| 1.7 | 12933 | 0.4845 | 1.460 | 0.4299 | 3.182 | 米谷 |
| 1.8 | 12993 | 0.4832 | 1.73 | 0.4298 | 3.19 | 沼野 |
| 1.9 | 11235 | 0.4783 | 2.73 | 0.4295 | 3.10 | 沼野 |
| 2 | 11456 | 0.4982 | 1.32 | 0.4296 | 3.12 | 沼野 |
| 3 | 2514 | 0.4369 | 4.87 | 0.4293 | 3.05 | 國井 |
| 4 | 1461 | 0.4341 | 4.20 | 0.4293 | 3.05 | 國井 |
| 5 | 433 | 0.2803 | 32.7 | 0.4284 | 2.83 | 國井 |
| 6 | 356 | 0.4283 | 2.80 | 0.3437 | 17.5 | 西澤 |
| 7 | 102 | 0.4260 | 2.26 | 0.2225 | 46.6 | 西澤 |
| 8 | 93 | 0.4260 | 2.26 | 0.1123 | 73.0 | 西澤 |
| 9 | 81 | 0.2212 | 54.9 | 0.4255 | 2.13 | 真庭 |
| 10 | 84 | 0.2051 | 58.3 | 0.4247 | 1.95 | 真庭 |
| 11 | 74 | 0.2260 | 54.0 | 0.4246 | 1.91 | 真庭 |
11/15 創造工房実習
Salome-Meca用いて単純梁を解き、中央断面の変位の平均を求めた。結果は図1のようになった。
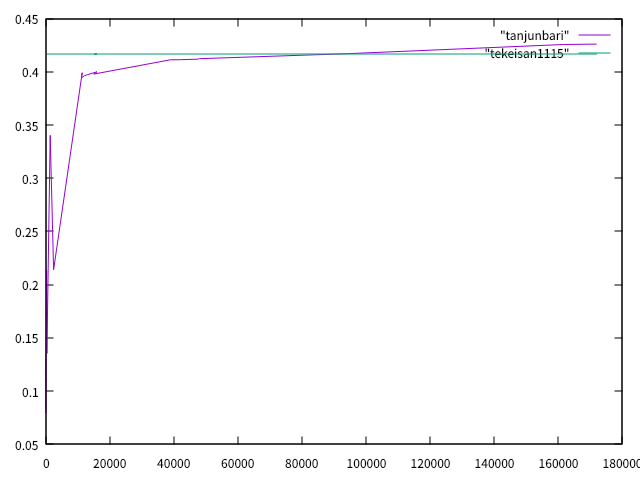
図1 単純梁 中央断面の変位 (X軸: 要素数, Y軸: 中央断面の変位)
「tekeisan1115」のグラフは単純梁の中央断面の変位の理論値を表している。今回は以下の条件で単純梁の中央に荷重を加えた。
・ヤング率E:6000 (MPa) =6000 (N/mm^2)
・ポアソン比ν:0.4
・単純梁全体の長さ : 120(mm)
・ピン支点の位置 : 10 (mm)
・ローラー支点の位置 : 110 (mm)
・支点間距離: 100 (mm )
・断面:10mm×10mm
・線荷重:10 (N/mm)
・中央断面にかかる荷重P : 10 (N/mm)×10(mm)=100(N)
・断面二次モーメントI : (10×10^3) / 12 (mm^4)
これらの条件より理論上の変位は次のようになる
PL^3/48EI = (100×100^3×12) / (48×6000×10×10^3) (mm) =0.4166666667 (mm) ≒0.4167 (mm)
「tanjunbari」のグラフはSalome-Meca用いて解いた単純梁の中央断面の変位の平均(実験値)を表している。このグラフ作成に用いたデータは以下の表のとおりである。
| メッシュ長さ | 要素数 | 先端変位(4隅の平均値)[mm] | 相対誤差(\( \frac{salome-手計算}{手計算} \)) | 計算者 |
| 0.7 | 171996 | 0.4260 | 2.207 | 湊 |
| 0.8 | 161561 | 0.4256 | 2.115 | 湊 |
| 0.9 | 94185 | 0.4169 | 0.0719 | 湊 |
| 1.1 | 47998 | 0.4122 | 1.067 | 森井 |
| 1.2 | 47343 | 0.4118 | 1.166 | 森井 |
| 1.3 | 42112 | 0.4113 | 1.289 | 森井 |
| 1.4 | 38960 | 0.4112 | 1.313 | 森井 |
| 1.5 | 15041 | 0.3978 | 4.516 | 米谷 |
| 1.6 | 16071 | 0.3999 | 4.002 | 米谷 |
| 1.7 | 12993 | 0.3971 | 4.687 | 米谷 |
| 1.8 | 12203 | 0.3964 | 4.85 | 沼野 |
| 1.9 | 11235 | 0.3942 | 5.38 | 沼野 |
| 2 | 11456 | 0.3991 | 4.20 | 沼野 |
| 3 | 2514 | 0.2141 | 21.4 | 國井 |
| 4 | 1461 | 0.34028 | 18.4 | 國井 |
| 5 | 433 | 0.1354 | 67.8 | 國井 |
| 6 | 356 | 0.2135 | 48.8 | 西澤 |
| 7 | 102 | 0.11 | 73.6 | 西澤 |
| 8 | 93 | 0.112 | 73.0 | 西澤 |
| 9 | 81 | 0.1125 | 73.0 | 真庭 |
| 10 | 84 | 0.0794 | 80.9 | 真庭 |
| 11 | 74 | 0.1297 | 68.9 | 真庭 |
図1より、要素数が35000を超えてくると理論値と実験値の値の差が小さくなった。表より、要素数が35000を超えてくるのはメッシュの長さが1.5よりも短い場合であり、このくらいの長さから誤差が小さくなることが分かる。また、前回と比較すると、前回は理論値よりも実験値が大きくなることはなかったが、今回は理論値よりも実験値の方が大きくなる時があり違いが見られる。これは梁や載荷する箇所の違いによる影響だと考えるが、そのあたりについて今後調べてみたいと思った。「
11/8 創造工房実習 Salome-Meca用いて片持ち梁を解き、自由端4すみの変位を求めた。結果は図1のようになった。
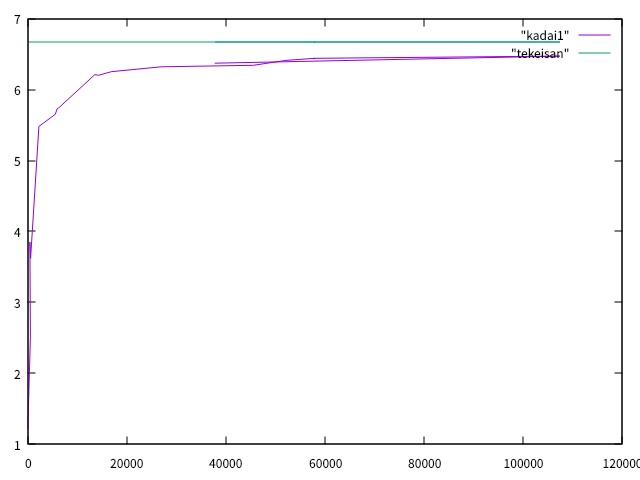
図1 片持ち梁 自由端の変位の平均 (X軸: 要素数, Y軸: 変位の平均)
「Tekeisan」 のグラフは片持ち梁の変位の理論値を表している。今回は以下の条件で片持ち梁の先端に荷重を加えた。
・ヤング率E:6000 (MPa) =6000 (N/mm^2)
・ポアソン比ν:0.4
・梁の軸長L: 100 (mm )
・断面:10mm×10mm
・先端荷重P:100 (N)
・断面二次モーメントI : (10×10^3) / 12 (mm^4)
これらの条件より理論上の変位は次のようになる
PL^3/3EI = (100×100^3×12) / (3×6000×10×10^3) (mm) =6.66666 (mm) ≒6.67 (mm)
「kadai1」のグラフはSalome-Meca用いて解いた片持ち梁の自由端4すみの変位の平均を表している。このグラフ作成に用いたデータは以下の表のとおりである。
例)メッシュ長さ1の場合(人によって多少の数値の誤差はあるので、こちらの数値は参考程度に)
| メッシュ長さ | 要素数 | 先端変位(4隅の平均値)[mm] | 相対誤差(\( \frac{salome-手計算}{手計算} \)) | 計算者 |
| 1 | 37757 | 6.37 | 4.5 | 創造工房 |
| 0.7 | 107380 | 6.47 | 2.96 | 湊 |
| 0.8 | 57821 | 6.44 | 3.62 | 湊 |
| 0.9 | 57698 | 6.43 | 3.73 | 湊 |
| 1.1 | 57980 | 6.44 | 3.57 | 湊 |
| 1.2 | 52123 | 6.41 | 3.90 | 森井 |
| 1.3 | 45549 | 6.34 | 4.98 | 森井 |
| 1.4 | 26951 | 6.32 | 5.31 | 森井 |
| 1.5 | 16904 | 6.25 | 6.32 | 米谷 |
| 1.6 | 14296 | 6.20 | 7.05 | 米谷 |
| 1.7 | 13596 | 6.21 | 6.81 | 米谷 |
| 1.8 | 6299 | 5.74 | 13.9 | 沼野 |
| 1.9 | 6001 | 5.73 | 14.1 | 沼野 |
| 2 | 5617 | 5.65 | 15.3 | 沼野 |
| 3 | 2309 | 5.48 | 17.8 | 國井 |
| 4 | 617 | 3.62 | 45.6 | 國井 |
| 5 | 494 | 3.85 | 42.3 | 國井 |
| 6 | 581 | 2.51 | 62.4 | 西澤 |
| 7 | 133 | 1.41 | 78.8 | 西澤 |
| 8 | 78 | 1.29 | 80.7 | 西澤 |
| 9 | 72 | 1.288 | 80.69 | 真庭 |
| 10 | 60 | 1.226 | 81.62 | 真庭 |
| 11 | 65 | 1.231 | 81.54 | 真庭 |
図1より、要素数が増える(メッシュの長さが短くなる)程、理論値に値が近づいていくことが分かった。今回変位を検証した時よりもメッシュの長さを短くするとより理論値に近づくと考えられる。
11/1 創造工房実習 gnuplotによるグラフの作成を行った。 1つ目 自分で打ち込んだデータ 2つ目 先輩方のデータをコピーしたもの*
*2023年11月17日(創造工房第4回) サロメ(片持ち梁)
コピーした先輩方のデータは下の表の通りである。
| 0.7 | 155192 | 0.08378905246 | 15.365 | 安藤 |
| 0.8 | 138808 | 0.08380386491 | 15.350 | 安藤 |
| 0.9 | 82587 | 0.083707073981 | 15.45 | 兼田 |
| 1.1 | 38671 | 0.084201207602 | 14.95 | 兼田 |
| 1.2 | 31929 | 0.083688 | 15.466 | 柴田 |
| 1.3 | 28621 | 0.083669 | 15.4857 | 柴田 |
| 1.4 | 28854 | 0.08368 | 15.47 | 佐藤 |
| 1.5 | 20015 | 0.084052 | 15.10 | 佐藤 |
| 1.6 | 19448 | 0.0835402938 | 15.62 | 皆川 |
| 1.7 | 13801 | 0.0834355098 | 15.72 | 皆川 |
| 1.8 | 12528 | 0.083733 | 15.42 | 永山 |
| 1.9 | 11769 | 0.083924 | 15.23 | 永山 |
| 2 | 10699 | 0.084076876559 | 15.074 | 辻 |
| 3 | 3579 | 0.08414561753 | 15.004 | 辻 |
| 4 | 1628 | 0.082794 | 16.37 | 服部 |
| 5 | 1016 | 0.083033 | 18.89 | 服部 |
| 6 | 839 | -0.082882 | 16.26 | 梶原 |
| 7 | 554 | -0.080871 | 18.28 | 梶原 |
| 8 | 285 | 0.079995 | 19.20 | 工藤 |
| 9 | 261 | 0.078980 | 20.22 | 工藤 |
| 10 | 232 | 0.081911 | 17.26 | 佐々木 |
| 11 | 208 | 0.075676 | 23.56 | 佐々木 |
10/11 今日は顔合わせを行った。