春休み課題†
振動班†
- 細長い長方形断面の梁(想像しやすい材料と大きさ)の梁
- 境界条件は単純梁、片持ち梁、両端固定、その他
- モード解析で、曲げ振動(縦方向、横方向)、ねじれ振動の1次、2次、それ以上のモードの固有振動数と振動モードを求める
- 上記の理論値を求め、比較する
- 梁の細長さや要素数を変え、収束値が理論値に近くなる条件を考察
梁条件†
単位:mm
鋼材(E=206000MPa)で解析
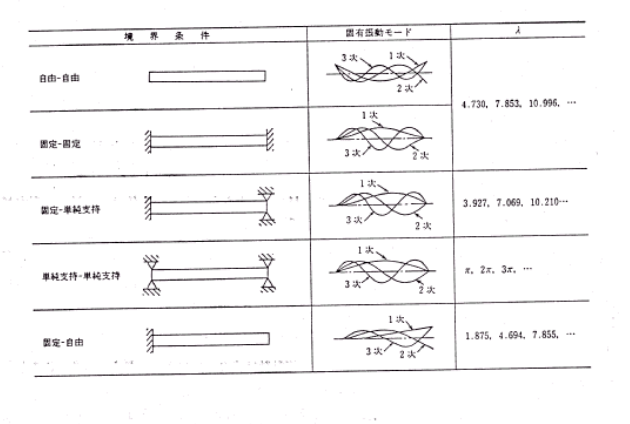
- 鉛直・水平モードの理論式 \( f = \frac{ω}{2π} \)=\( \frac{1}{2π}\frac{λ^{2}}{l^{2}}\sqrt{\frac{EI}{ρA}} \)
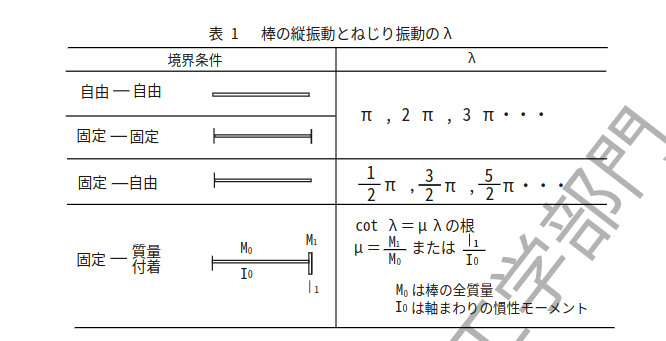
- ねじれモードの理論式 \( f= \frac{\lambda}{2\pi\ell}\times \sqrt{\frac{GJ}{\rho I_p}} \)
(λ:無次元定数 L:長さ E:ヤング率 I:断面二次モーメント ρ:密度 A:断面積 f:固有振動数 G:せん断補正係数 J:ねじり定数 GJ:ねじれ剛性 Ip:断面2次極モーメント)
λ・・・下記の図中に書いてある数値がそれに当たる。
f・・・固有振動数=10コ or 20コ で入力
やること†


解析結果†
単純梁1【幅10×厚さ5×長さ520(スパン長500)】かつ【メッシュ0.7~4.0】†
| メッシュの長さ | 要素数 | 鉛直1次の固有振動数解析値 | 相対誤差 |
| 0.7 | 326123 | 74.71 | 2.595% |
| 0.8 | 242092 | 75.17 | 3.227% |
| 0.9 | 242373 | 74.96 | 2.939% |
| 1.0 | 155734 | 75.71 | 3.969% |
| 2.0 | 25757 | 83.00 | 13.980% |
| 3.0 | 5141 | 122.33 | 67.990% |
| 4.0 | 1925 | 149.09 | 104.738% |
| メッシュの長さ | 要素数 | 鉛直2次の固有振動数解析値 | 相対誤差 |
| 0.7 | 326123 | 241.95 | 2.534% |
| 0.8 | 242092 | 243.41 | 3.153% |
| 0.9 | 242373 | 242.74 | 2.869% |
| 1.0 | 155734 | 245.16 | 3.895% |
| 2.0 | 25757 | 268.60 | 13.828% |
| 3.0 | 5141 | 398.78 | 68.996% |
| 4.0 | 1925 | 482.02 | 104.272% |
| メッシュの長さ | 要素数 | 鉛直3次の固有振動数解析値 | 相対誤差 |
| 0.7 | 326123 | 504.18 | 2.421% |
| 0.8 | 242092 | 507.28 | 3.051% |
| 0.9 | 242373 | 505.90 | 2.771% |
| 1.0 | 155734 | 510.92 | 3.791% |
| 2.0 | 25757 | 560.00 | 13.761% |
| 3.0 | 5141 | 825.18 | 67.631% |
| 4.0 | 1925 | 1002.64 | 103.681% |
| メッシュの長さ | 要素数 | 水平1次の固有振動数解析値 | 相対誤差 |
| 0.7 | 326123 | 145.04 | 0.419% |
| 0.8 | 242092 | 145.38 | 0.185% |
| 0.9 | 242373 | 145.28 | 0.254% |
| 1.0 | 155734 | 145.77 | 0.082% |
| 2.0 | 25757 | 149.60 | 2.712% |
| 3.0 | 5141 | 158.82 | 9.042% |
| 4.0 | 1925 | 172.47 | 18.414% |
| メッシュの長さ | 要素数 | 水平2次の固有振動数解析値 | 相対誤差 |
| 0.7 | 326123 | 468.76 | 0.676% |
| 0.8 | 242092 | 469.83 | 0.449% |
| 0.9 | 242373 | 469.53 | 0.513% |
| 1.0 | 155734 | 471.07 | 0.186% |
| 2.0 | 25757 | 483.18 | 2.379% |
| 3.0 | 5141 | 513.37 | 8.776% |
| 4.0 | 1925 | 557.17 | 18.057% |
| メッシュの長さ | 要素数 | 水平3次の固有振動数解析値 | 相対誤差 |
| 0.7 | 326123 | 974.1 | 1.060% |
| 0.8 | 242092 | 976.34 | 0.832% |
| 0.9 | 242373 | 975.69 | 0.898% |
| 1.0 | 155734 | 978.92 | 0.570% |
| 2.0 | 25757 | 1004.01 | 1.979% |
| 3.0 | 5141 | 1066.45 | 8.321% |
| 4.0 | 1925 | 1157.08 | 17.526% |
| メッシュの長さ | 要素数 | 鉛直1次の固有振動数解析値 | 相対誤差 |
| 0.7 | | | % |
| 0.8 | | | % |
| 0.9 | | | % |
| 1.0 | 155734 | 72.57 | 0.343% |
| 2.0 | 25757 | 72.68 | 0.192% |
| 3.0 | 5141 | 72.79 | 0.041% |
| 4.0 | 1925 | 72.87 | 0.069% |
| メッシュの長さ | 要素数 | 鉛直2次の固有振動数解析値 | 相対誤差 |
| 0.7 | | | % |
| 0.8 | | | % |
| 0.9 | | | % |
| 1.0 | 155734 | 235.02 | 0.403% |
| 2.0 | 25757 | 235.36 | 0.259% |
| 3.0 | 5141 | 235.73 | 0.102% |
| 4.0 | 1925 | 235.98 | 0.004% |
| メッシュの長さ | 要素数 | 鉛直3次の固有振動数解析値 | 相対誤差 |
| 0.7 | | | % |
| 0.8 | | | % |
| 0.9 | | | % |
| 1.0 | 155734 | 489.81 | 0.498% |
| 2.0 | 25757 | 490.52 | 0.353% |
| 3.0 | 5141 | 491.33 | 0.189% |
| 4.0 | 1925 | 491.89 | 0.075% |
| メッシュの長さ | 要素数 | 水平1次の固有振動数解析値 | 相対誤差 |
| 0.7 | | | % |
| 0.8 | | | % |
| 0.9 | | | % |
| 1.0 | 155734 | 143.33 | 1.593% |
| 2.0 | 25757 | 144.00 | 1.133% |
| 3.0 | 5141 | 144.26 | 0.954% |
| 4.0 | 1925 | 144.86 | 0.542% |
| メッシュの長さ | 要素数 | 水平2次の固有振動数解析値 | 相対誤差 |
| 0.7 | | | % |
| 0.8 | | | % |
| 0.9 | | | % |
| 1.0 | 155734 | 463.33 | 1.826% |
| 2.0 | 25757 | 465.41 | 1.386% |
| 3.0 | 5141 | 466.24 | 1.210% |
| 4.0 | 1925 | 468.14 | 0.807% |
| メッシュの長さ | 要素数 | 水平3次の固有振動数解析値 | 相対誤差 |
| 0.7 | | | % |
| 0.8 | | | % |
| 0.9 | | | % |
| 1.0 | 155734 | 963.03 | 2.184% |
| 2.0 | 25757 | 967.18 | 1.762% |
| 3.0 | 5141 | 968.85 | 1.593% |
| 4.0 | 1925 | 972.74 | 1.200% |
| メッシュの長さ | 要素数 | ねじれ1次の固有振動数解析値 | 相対誤差 |
| 0.7 | | | % |
| 0.8 | | | % |
| 0.9 | | | % |
| 1.0 | 155734 | 2363.68 | 0.104% |
| 2.0 | 25757 | 2372.26 | 0.467% |
| 3.0 | 5141 | 2389.47 | 1.196% |
| 4.0 | 1925 | 2463.83 | 4.345% |
| メッシュの長さ | 要素数 | ねじれ2次の固有振動数解析値 | 相対誤差 |
| 0.7 | | | % |
| 0.8 | | | % |
| 0.9 | | | % |
| 1.0 | 155734 | 4727.77 | 0.112% |
| 2.0 | 25757 | 4744.94 | 0.476% |
| 3.0 | 5141 | 4779.53 | 1.208% |
| 4.0 | 1925 | 4928.45 | 4.362% |
片持ち梁1【幅20×厚さ10×長さ100】かつ【メッシュ0.7~4.0】†
両端固定1【幅20×厚さ10×長さ100】かつ【メッシュ0.7~4.0】†
1次要素 鉛直1〜3次、水平1〜3次、ねじれ1,2次
| メッシュの長さ | 要素数 | 鉛直1次の固有振動数解析値 | 相対誤差 |
| 0.7 | 309271 | 108.745 | 2.929% |
| 0.8 | 260320 | 109.058 | 3.226% |
| 0.9 | 182242 | 109.863 | 3.988% |
| 1.0 | 156815 | 109.81 | 3.938% |
| 2.0 | 22223 | 122.418 | 15.87% |
| 3.0 | 4525 | 187.602 | 77.57% |
| 4.0 | 1842 | 149.09 | 103.11% |
| メッシュの長さ | 要素数 | 鉛直2次の固有振動数解析値 | 相対誤差 |
| 0.7 | 326123 | 299.484 | 2.839% |
| 0.8 | 242092 | 300.352 | 3.137% |
| 0.9 | 242373 | 302.606 | 3.910% |
| 1.0 | 155734 | 302.379 | 3.832% |
| 2.0 | 25757 | 337.294 | 15.822% |
| 3.0 | 5141 | 517.391 | 77.665% |
| 4.0 | 1925 | 590.333 | 102.71% |
| メッシュの長さ | 要素数 | 鉛直3次の固有振動数解析値 | 相対誤差 |
| 0.7 | 326123 | 586.424 | 2.706% |
| 0.8 | 242092 | 588.085 | 2.996% |
| 0.9 | 242373 | 592.52 | 3.773% |
| 1.0 | 155734 | 592.25 | 3.726% |
| 2.0 | 25757 | 660.369 | 15.656% |
| 3.0 | 5141 | 1013.05 | 77.425% |
| 4.0 | 1925 | 1153.78 | 102.072% |
| メッシュの長さ | 要素数 | 水平1次の固有振動数解析値 | 相対誤差 |
| 0.7 | 326123 | 212.501 | 0.568% |
| 0.8 | 242092 | 212.646 | 0.637% |
| 0.9 | 242373 | 213.044 | 0.825% |
| 1.0 | 155734 | 213.128 | 0.865% |
| 2.0 | 25757 | 218.382 | 3.351% |
| 3.0 | 5141 | 237.243 | 12.277% |
| 4.0 | 1925 | 250.047 | 18.337% |
| メッシュの長さ | 要素数 | 水平2次の固有振動数解析値 | 相対誤差 |
| 0.7 | 326123 | 583.7 | 0.217% |
| 0.8 | 242092 | 584.1 | 0.286% |
| 0.9 | 242373 | 585.221 | 0.478% |
| 1.0 | 155734 | 585.438 | 0.515% |
| 2.0 | 25757 | 599.796 | 2.980% |
| 3.0 | 5141 | 652.345 | 12.003% |
| 4.0 | 1925 | 686.783 | 17.916% |
| メッシュの長さ | 要素数 | 水平3次の固有振動数解析値 | 相対誤差 |
| 0.7 | 326123 | 1138.91 | 0.266% |
| 0.8 | 242092 | 1139.68 | 0.198% |
| 0.9 | 242373 | 1141.9 | 0.00437% |
| 1.0 | 155734 | 1142.37 | 0.0367% |
| 2.0 | 25757 | 1170.35 | 2.486% |
| 3.0 | 5141 | 1273.39 | 11.510% |
| 4.0 | 1925 | 1339.53 | 17.301% |
| メッシュの長さ | 要素数 | ねじれ1次の固有振動数解析値 | 相対誤差 |
| 0.7 | 326123 | 2470.84 | 4.642% |
| 0.8 | 242092 | 2476.12 | 4.865% |
| 0.9 | 242373 | 2503.46 | 6.023% |
| 1.0 | 155734 | 2511.73 | 6.373% |
| 2.0 | 25757 | 2861.31 | 21.178% |
| 3.0 | 5141 | 3904.46 | 65.357% |
| 4.0 | 1925 | 4597.8 | 94.720% |
| メッシュの長さ | 要素数 | ねじれ2次の固有振動数解析値 | 相対誤差 |
| 0.7 | 326123 | 4942.6 | 4.661% |
| 0.8 | 242092 | 4953.03 | 4.882% |
| 0.9 | 242373 | 5006.85 | 6.022% |
| 1.0 | 155734 | 5024.52 | 6.396% |
| 2.0 | 25757 | 5715.06 | 21.018% |
| 3.0 | 5141 | 7805.99 | 65.294% |
| 4.0 | 1925 | 9198.64 | 94.784% |
一端固定他端単純支持梁1【幅10×厚さ5×長さ510】かつ【メッシュ0.7~4.0】かつ 【ローラー1コ】†
| メッシュの長さ | 要素数 | 鉛直1次の固有振動数解析値 | 相対誤差 |
| 0.7 | 315209 | 74.8789 | 2.607% |
| 0.8 | 230838 | 75.4138 | 3.556% |
| 0.9 | 177829 | 75.7717 | 4.048% |
| 1.0 | 152697 | 75.4951 | 4.080% |
| 2.0 | 23836 | 84.3412 | 15.815% |
| 3.0 | 4620 | 130.984 | 70.221% |
| 4.0 | 1845 | 133.022 | 82.662% |
| メッシュの長さ | 要素数 | 鉛直2次の固有振動数解析値 | 相対誤差 |
| 0.7 | 315209 | 242.47 | 2.752% |
| 0.8 | 230838 | 244.191 | 3.481% |
| 0.9 | 177829 | 245.324 | 3.961% |
| 1.0 | 152697 | 245.418 | 4.001% |
| 2.0 | 23836 | 273.259 | 15.799% |
| 3.0 | 4620 | 424.377 | 79.839% |
| 4.0 | 1845 | 426.36 | 80.679% |
| メッシュの長さ | 要素数 | 鉛直3次の固有振動数解析値 | 相対誤差 |
| 0.7 | 315209 | 505.33 | 2.653% |
| 0.8 | 230838 | 508.949 | 3.388% |
| 0.9 | 177829 | 511.328 | 3.871% |
| 1.0 | 152697 | 511.474 | 3.901% |
| 2.0 | 23836 | 569.715 | 15.732% |
| 3.0 | 4620 | 883.493 | 79.473% |
| 4.0 | 1845 | 887.109 | 80.207% |
| メッシュの長さ | 要素数 | 水平1次の固有振動数解析値 | 相対誤差 |
| 0.7 | 315209 | 146.488 | 0.578% |
| 0.8 | 230838 | 146.749 | 0.752% |
| 0.9 | 177829 | 146.898 | 0.860% |
| 1.0 | 152697 | 147.002 | 0.931% |
| 2.0 | 23836 | 150.494 | 3.329% |
| 3.0 | 4620 | 163.309 | 12.127% |
| 4.0 | 1845 | 169.007 | 16.040% |
| メッシュの長さ | 要素数 | 水平2次の固有振動数解析値 | 相対誤差 |
| 0.7 | 315209 | 473.358 | 0.299% |
| 0.8 | 230838 | 474.196 | 0.477% |
| 0.9 | 177829 | 474.685 | 0.580% |
| 1.0 | 152697 | 475.042 | 0.656% |
| 2.0 | 23836 | 486.24 | 3.029% |
| 3.0 | 4620 | 527.948 | 11.866% |
| 4.0 | 1845 | 545.239 | 15.530% |
| メッシュの長さ | 要素数 | 水平3次の固有振動数解析値 | 相対誤差 |
| 0.7 | 315209 | 983.482 | 0.106% |
| 0.8 | 230838 | 985.251 | 0.073% |
| 0.9 | 177829 | 986.269 | 0.177% |
| 1.0 | 152697 | 986.934 | 0.244% |
| 2.0 | 23836 | 1010.11 | 2.598% |
| 3.0 | 4620 | 1097.19 | 11.443% |
| 4.0 | 1845 | 1132.94 | 15.074% |
一端固定他端単純支持梁2【幅10×厚さ5×長さ510】かつ【メッシュ0.7~4.0】かつ 【ローラー2コ】†
| メッシュの長さ | 要素数 | 鉛直1次の固有振動数解析値 | 相対誤差 |
| 0.7 | 312083 | 74.8786 | 2.821% |
| 0.8 | 228420 | 75.4049 | 3.544% |
| 0.9 | 175051 | 75.7272 | 3.987% |
| 1.0 | 153440 | 75.7581 | 4.029% |
| 2.0 | 25064 | 84.9083 | 13.847% |
| 3.0 | 5089 | 121.944 | 67.450% |
| 4.0 | 1877 | 148.55 | 103.984% |
| メッシュの長さ | 要素数 | 鉛直2次の固有振動数解析値 | 相対誤差 |
| 0.7 | 312083 | 242.459 | 2.747% |
| 0.8 | 228420 | 244.144 | 3.461% |
| 0.9 | 175051 | 245.216 | 3.916% |
| 1.0 | 153440 | 245.289 | 3.947% |
| 2.0 | 25064 | 268.525 | 13.793% |
| 3.0 | 5089 | 397.905 | 68.621% |
| 4.0 | 1877 | 480.751 | 103.729% |
| メッシュの長さ | 要素数 | 鉛直3次の固有振動数解析値 | 相対誤差 |
| 0.7 | 312083 | 505.287 | 2.644% |
| 0.8 | 228420 | 508.831 | 3.364% |
| 0.9 | 175051 | 511.063 | 3.817% |
| 1.0 | 153440 | 511.186 | 3.842% |
| 2.0 | 25064 | 559.262 | 13.609% |
| 3.0 | 5089 | 826.065 | 67.807% |
| 4.0 | 1877 | 1000.45 | 103.232% |
| メッシュの長さ | 要素数 | 水平1次の固有振動数解析値 | 相対誤差 |
| 0.7 | 312083 | 146.486 | 0.577% |
| 0.8 | 228420 | 146.757 | 0.763% |
| 0.9 | 175051 | 146.883 | 0.849% |
| 1.0 | 153440 | 146.98 | 0.916% |
| 2.0 | 25064 | 149.99 | 2.280% |
| 3.0 | 5089 | 159.59 | 9.574% |
| 4.0 | 1877 | 172.491 | 18.432% |
| メッシュの長さ | 要素数 | 水平2次の固有振動数解析値 | 相対誤差 |
| 0.7 | 312083 | 473.349 | 0.297% |
| 0.8 | 228420 | 474.219 | 0.481% |
| 0.9 | 175051 | 474.638 | 0.570% |
| 1.0 | 153440 | 474.948 | 0.636% |
| 2.0 | 25064 | 484.675 | 2.697% |
| 3.0 | 5089 | 515.887 | 9.310% |
| 4.0 | 1877 | 557.431 | 18.113% |
| メッシュの長さ | 要素数 | 水平3次の固有振動数解析値 | 相対誤差 |
| 0.7 | 312083 | 983.506 | 0.104% |
| 0.8 | 228420 | 985.308 | 0.079% |
| 0.9 | 175051 | 986.182 | 0.168% |
| 1.0 | 153440 | 986.783 | 0.229% |
| 2.0 | 25064 | 1007.07 | 2.289% |
| 3.0 | 5089 | 1071.56 | 8.840% |
| 4.0 | 1877 | 1157.82 | 17.601% |
一端固定他端単純支持梁3【幅10×厚さ5×長さ510】かつ【メッシュ1.0~10.0】かつ 【ローラー1コ】かつ【2次要素】†
| メッシュの長さ | 要素数 | 鉛直1次の固有振動数解析値 | 相対誤差 |
| 1.0 | 152697 | 72.8441 | 0.028% |
| 1.5 | 36859 | 72.8486 | 0.034% |
| 2.0 | 23836 | 72.8519 | 0.038% |
| 4.0 | 1845 | 72.8932 | 0.095% |
| 10.0 | 306 | 73.0522 | 0.313% |
| メッシュの長さ | 要素数 | 鉛直2次の固有振動数解析値 | 相対誤差 |
| 1.0 | 152697 | 235.881 | 0.040% |
| 1.5 | 36859 | 235.896 | 0.034% |
| 2.0 | 23836 | 235.907 | 0.029% |
| 4.0 | 1845 | 236.064 | 0.037% |
| 10.0 | 306 | 236.671 | 0.295% |
| メッシュの長さ | 要素数 | 鉛直3次の固有振動数解析値 | 相対誤差 |
| 1.0 | 152697 | 491.586 | 0.139% |
| 1.5 | 36859 | 491.619 | 0.132% |
| 2.0 | 23836 | 491.645 | 0.127% |
| 4.0 | 1845 | 492.044 | 0.046% |
| 10.0 | 306 | 493.622 | 0.274% |
| メッシュの長さ | 要素数 | 水平1次の固有振動数解析値 | 相対誤差 |
| 1.0 | 152697 | 145.467 | 0.123% |
| 1.5 | 36859 | 145.476 | 0.117% |
| 2.0 | 23836 | 145.481 | 0.113% |
| 4.0 | 1845 | 145.518 | 0.088% |
| 10.0 | 306 | 145.827 | 0.124% |
| メッシュの長さ | 要素数 | 水平2次の固有振動数解析値 | 相対誤差 |
| 1.0 | 152697 | 470.053 | 0.401% |
| 1.5 | 36859 | 470.086 | 0.394% |
| 2.0 | 23836 | 470.105 | 0.390% |
| 4.0 | 1845 | 470.241 | 0.361% |
| 10.0 | 306 | 471.487 | 0.097% |
| メッシュの長さ | 要素数 | 水平3次の固有振動数解析値 | 相対誤差 |
| 1.0 | 152697 | 976.59 | 0.806% |
| 1.5 | 36859 | 976.665 | 0.799% |
| 2.0 | 23836 | 976.715 | 0.794% |
| 4.0 | 1845 | 977.041 | 0.761% |
| 10.0 | 306 | 980.413 | 0.418% |
\( f= \frac{\lambda}{2\pi\ell}\times \sqrt{\frac{GJ}{\rho I_p}} \)
=2361.23 Hz (1次)
=4722.46 Hz (2次)
上記は両端固定のλを使用している。しかし、両端単純梁・一端固定他端単純支持梁ともに相対誤差を計算すると合っているように感じる。
振動の仕方に大差ないことから同じλを使用しても問題ないのではないだろうか。
| メッシュの長さ | 要素数 | ねじれ1次の固有振動数解析値 | 相対誤差 |
| 1.0 | 152697 | 2358.04 | 0.135% |
| 1.5 | 36859 | 2361.8 | 0.024% |
| 2.0 | 23836 | 2366.47 | 0.222% |
| 4.0 | 1845 | 2469.7 | 4.594% |
| 10.0 | 306 | 2559.2 | 8.384% |
| メッシュの長さ | 要素数 | ねじれ2次の固有振動数解析値 | 相対誤差 |
| 1.0 | 152697 | 4722.96 | 0.011% |
| 1.5 | 36859 | 4727.05 | 0.101% |
| 2.0 | 23836 | 4734.36 | 0.256% |
| 4.0 | 1845 | 4939.29 | 4.596% |
| 10.0 | 306 | 5122.04 | 8.466% |
2次要素で解析した場合は、鉛直・水平モードは収束したがねじれモードは収束しなかった。
面内は考えている面の水平方向を意味する。面外は考えている面との直交方向を意味する。
平面内に横たわる構造系がその平面内で荷重載荷を受けていながら、その平面から外に飛び出してたわむような座屈をする場合、この座屈を「横倒れ座屈」とか「面外座屈」と言う。これに対して載荷平面内で生じる座屈は「面内座屈」と言う。
平面内に載荷を受ける構造部材では、この面内で強度を発揮するのが目的だから一般に面内の剛性を最も大きくとっているが、相対的に面外の剛性は低くなるので面内座屈よりも面外座屈が構造部材の強度を支配することは少くない。
自由端は、位相のズレがなくそのまま壁にぶつかった形で反射する。
固定端は、位相がπズレて反射する。
構造物が持つ固有の共振周波数のことである。
形状・拘束位置・材料のヤング率や密度によって異なる。
v = f ×λ
また、対象物が自由振動を行うときの単位時間に起こる往復運動の回数のことであり、1秒間に10往復であれば固有振動数は10Hzとなる。
固有振動数は質量が大きくなるほど低くなり、剛性が高くなるほど高くなる。
固有振動数が重要である最も大きな理由は、共振を避けて破損や機能障害を防ぐことである。
構造物の振動特性をモードの重ね合わせで表現する解析方法を指す。
「モード」とは「振動モード」または「振動形態」を意味する。
固有周波数とその周波数での振動形状を調べる解析がモード解析(固有値解析)である。
梁やスラブの支持条件をいうとき、一端が固定で他端が違う支持条件のこと。不静定梁である。
振動の変位方向によって、鉛直、水平、ねじれの3種類に分類できる模様(他にもあるかも)。振動の仕方はParaVisより確認できる。スクショを貼った方が分かりやすいので、余裕があれば貼ります。鉛直、水平、ねじれによって理論式が変わるみたいなので現在調べ中(日本機械学会のページがなくなってしまった)。
両端ピン支持・片側ピン・片側ローラー支持の支持条件をいう。全てにおいて支点曲げモーメントが生じない。
単純支持は、両端に曲げモーメントが生じない静定構造のことである。
曲げモーメントとは、部材を曲げようとする力のこと。
力が作用すると、もとに戻ろうとする力が働くことにより、振動が生じる。
ねじれの力に抵抗する性質を持つもの。
細長いよりも太短いほうがねじれやすい。
参考資料†
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)