[Googleで検索] [ウィキペディア] [IT用語辞典] [秋田大学蔵書検索システム] [ シラバス ] (土木環境工学実験) (情報処理の技法) (後藤資料)

構造力学(準備開始)
静定梁のたわみ

注意： このページの数式は、 MathJaxを使って書いてます。 数式部分がおかしい場合は、更新ボタンをクリックすると 改善するかも知れません。 太文字のギリシャ文字($\mathbf{\sigma}$など)が、 太文字になっていない($\sigma$)かもしれません。 印刷版で確認して下さい。 その他、おかしい記述があると思ったら、 メールなどで指摘して下さい。

構造力学ウェブテキストへ戻る

目次

境界値問題

断面力の章で、断面の 曲げモーメントとたわみの関係が
$M(z)= -EI\frac{d^{2}v(z)}{dz^{2}}$
と表されることが示された。 曲げモーメント$M(z)$がたわみ$v(z)$の2階微分で表されているということは、 曲げモーメント分布が力のつりあいで求まる静定梁なら、 これを$z$について2回積分すればたわみ$v(z)$を$z$の関数として求めることが できそうである。

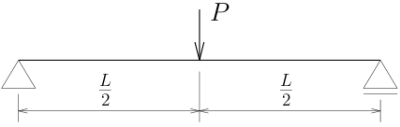
./png/tanzyun.png という訳で、 図のような中央に集中荷重を受ける単純支持梁について、 上の2階の微分方程式を使ってたわみを求めてみる。 梁の左端を原点として梁軸に沿って右側正に$z$軸を取る。 この梁の曲げモーメント分布は、 まずは基礎(の復習) の章の断面力の計算の節 の梁と同じなので(軸力は曲げモーメントのつりあいに関係しないから)、

$M(z)=\frac{P}{2}z$   $(0\le z\le\frac{L}{2})$
$M(z)=\frac{P}{2}(L-z)$   $(\frac{L}{2}\le z\le L)$


となる。 便宜上、 $0\le z\le\frac{L}{2}$の左半分のたわみを$v_{左}$と書いて、 $\frac{L}{2}\le z\le L$ の右半分のたわみを$v_{右}$と書くことにし、 $\frac{d}{dz}$の微分を$'$で表して (例えば $M(z)= -EI\frac{d^{2}v(z)}{dz^{2}}$ を $M(z)=-EIv''$みたいに表記して)、 それぞれ$z$について 2回積分してみると、

$0\le z\le\frac{L}{2}$について
$-EIv''_{左}=\frac{P}{2}z$
$-EIv'_{左}=\frac{P}{4}z^{2}+A$
$-EIv_{左}=\frac{P}{12}z^{3}+Az+B$
$\frac{L}{2}\le z\le L$について
$-EIv''_{右}=\frac{P}{2}(L-z)$
$-EIv'_{右}=\frac{P}{2}(Lz-\frac{z^{2}}{2})+C$
$-EIv_{右}=\frac{P}{2}(\frac{L}{2}z^{2}-\frac{z^{3}}{6})+Cz+D$

となり、$A, B, C, D$の4つの積分定数が未知数となる。 この4つの未知数を求めるには、4つの条件式が必要になるが、 両端でたわみが0であるという境界条件
$v_{左}(0)=0$
$v_{右}(L)=0$
と、中央の載荷点でのたわみとたわみ角が一致するという 連続条件
$v_{左}(\frac{L}{2})=v_{右}(\frac{L}{2})$
$v'_{左}(\frac{L}{2})=v'_{右}(\frac{L}{2})$
を使えば条件式4つなので、4つの未知数$A, B, C, D$を 求めることができそうだ。 という訳で、これらの条件式を書き出してみると、
$v_{左}(0)=0$から$B=0$
$v_{右}(L)=0$から$LC+D=-\frac{PL^{3}}{6}$
$v_{左}(\frac{L}{2})=v_{右}(\frac{L}{2})$ から$\frac{L}{2}A-\frac{L}{2}C-D=\frac{PL^{3}}{24}$
$v'_{左}(\frac{L}{2})=v'_{右}(\frac{L}{2})$ から$A-C=\frac{PL^{2}}{8}$
という$A, B, C, D$に関する連立方程式になるので、 これを解くと、
$A=-\frac{PL^{2}}{16}$
$B=0$
$C=-\frac{3PL^{2}}{16}$
$D=\frac{PL^{3}}{48}$
と求まる。よって、これらを$v_{左}$と$v_{右}$に代入すると 梁のたわみは、
$v=\frac{P}{48EI}(3L^{2}z-4z^{3})$    $(0\le z\le\frac{L}{2})$
$v=\frac{P}{48EI}(4z^{3}-12Lz^{2}+9L^{2}z-L^{3})$    $(\frac{L}{2}\le z\le L)$
と求まる。
ちなみに、この問題は左右対称なので、載荷点の梁中央における たわみ角がたまたま0であるという条件を利用するなら、
$v'_{左}(\frac{L}{2})=0$から $A=-\frac{PL^{2}}{16}$を、
$v'_{右}(\frac{L}{2})=0$から $C=-\frac{3PL^{2}}{16}$を求めることもできる。
また、梁の左端から右端まで一様な(または傾き一定の)等分布荷重が 作用している問題など、$0 \le z \le L$の全領域で$v(z)$を ($v_{左}$と$v_{右}$みたいに)場合分けする必要のない問題では、 連続条件は不要なので境界条件だけで答えが求まる。
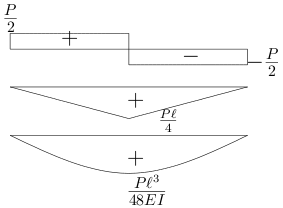
なお、載荷点の中央部のたわみは、 $v_{左}(\frac{L}{2})=v_{右}(\frac{L}{2})=\frac{PL^{3}}{48EI}$となる。 ./png/tanzyun.png

./png/tancsmvl.png

(目次)

単位荷重法

梁のたわみを求める問題は、 上の例のように微分方程式を境界値問題として解くのが 数学的な意味が明解な解き方だと思うが (だからこのテキストではこれを標準解法とするが)、 未知数の多い連立方程式を解く必要があるので、 手と鉛筆で解く場合にはそれなりにめんどくさくて 計算ミスをしやすい。 まあ、それでも任意点のたわみを$z$の関数として求める 必要がある場合には、この標準解法で解いていいと思う。 ただ、求めたいたわみが、特定の1点のたわみでいい場合、 その点のたわみだけを求めるには、 単位荷重法という便法が使えるので一応、 紹介しておく。 軸力の作用しない梁の問題なら、 曲げモーメント分布$M(z)$をまず求める(静定梁なら力のつりあいだけで求まる)。 次に、たわみを求めたい点に$P=1$の単位荷重を作用させた場合の 曲げモーメント分布$\bar{M}(z)$を求める。 すると、求めたい点のたわみは

$v=\int_{0}^{L}\frac{M(z)\bar{M}(z)}{EI}dz$

と求まる。なぜこの方法で求まるのかということについては、 このテキストのネタ本でもある 岩熊哲夫・小山茂『鬆徒労苦衷有迷禍荷苦痛-- 計算機による構造解析の基礎としての構造力学を独習する』 を参照してほしい。

./png/tanzyun.png 境界値問題の例題と同じ中央に集中荷重を 受ける単純梁の中央のたわみを単位荷重法で求めてみる。 まず、解くべき梁の曲げモーメント分布は、
$M_{左}(z)=\frac{P}{2}z$   $(0\le z\le\frac{L}{2})$
$M_{右}(z)=\frac{P}{2}(L-z)$   $(\frac{L}{2}\le z\le L)$
であり、

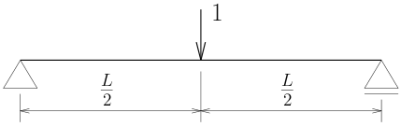./png/tani.png たわみを求めたい中央部に$P=1$の単位荷重を載荷した梁の 曲げモーメント分布は、
$M_{左}(z)=\frac{1}{2}z$   $(0\le z\le\frac{L}{2})$
$M_{右}(z)=\frac{1}{2}(L-z)$   $(\frac{L}{2}\le z\le L)$
である。すると、たわみは、
$v(\frac{L}{2}) =\int_{0}^{L}\frac{M(z)\bar{M}(z)}{EI}dz$
$=\int_{0}^{\frac{L}{2}}\frac{M_{左}(z)\bar{M}_{左}(z)}{EI}dz +\int_{\frac{L}{2}}^{L}\frac{M_{右}(z)\bar{M}_{右}(z)}{EI}dz$
$=\frac{1}{EI}\int_{0}^{\frac{L}{2}}\frac{P}{2}z\cdot \frac{1}{2}zdz +\frac{1}{EI}\int_{\frac{L}{2}}^{L} \frac{P}{2}(L-z)\cdot \frac{1}{2}(L-z)dz$
$=\frac{P}{4EI}\int_{0}^{\frac{L}{2}}z^{2}dz +\frac{P}{4EI}\int_{\frac{L}{2}}^{L} (L^{2}-2Lz+z^{2})dz$
$=\frac{P}{4EI}[\frac{z^{3}}{3}]_{0}^{\frac{L}{2}} +\frac{P}{4EI}[L^{2}z-lz^{2}+\frac{z^{3}}{3}]_{\frac{L}{2}}^{L}$
$=\frac{PL^{3}}{48EI}$
と求まる。
左右対称であるということを利用するなら、$0\le z\le \frac{L}{2}$ の左半分の積分だけ求めてそれを2倍するという手もある。

(目次)

練習問題

問1

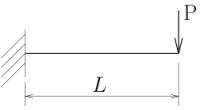./png/kata1.png 図の片持ち梁のたわみを座標($z$)の関数として求めよ。 曲げ剛性は$EI$としてよい。

解答

$M=P(z-L)$
$M=-EIv''$より
$EIv''=P(L-z)$
$EIv'=P(Lz-\frac{z^{2}}{2})+A$
$EIv=P(\frac{L}{2}z^{2}-\frac{z^{3}}{6})+Az+B$
境界条件:$v(0)=0, v'(0)=0$より$B=0, A=0$
$v=\frac{P}{6EI}(3Lz^{2}-z^{3})$
先端のたわみ：$v(L)=\frac{PL^{3}}{3EI}$

問2

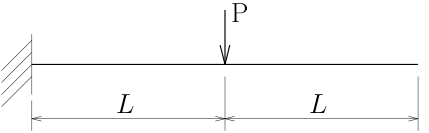./png/kata2.png 問1の結果を利用し、 図の片持ち梁のたわみを座標($z$)の関数として求めよ。 曲げ剛性は$EI$としてよい。

解答

$0\le z\le L$の部分は問1と同じ。
$L \le z \le 2L$のとき
$M=0$
$M=-EIv''$より、
$EIv''=0$
$EIv'=C$
$EIv=Cz+D$
連続条件: $v'_{左}(L)=v'_{右}(L)$, $v_{左}(L)=v_{右}(L)$より
$C=\frac{PL^{2}}{2}$, $D=-\frac{PL^{3}}{6}$
$v=\frac{P}{6EI}(3L^{2}z-L^{3})$
先端のたわみ: $v(2L)=\frac{5PL^{3}}{6EI}$ ./png/kata2.png

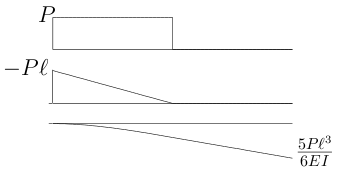
./png/katacsmv.png

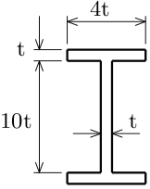./png/i.png また、この梁が図のような2軸対称のI型断面をしている場合、 直応力と曲げモーメントの関係を 用いて、直応力の最大値と、それが発生する場所$(y,z)$を求めよ。

解答

$I=\frac{4t(12t)^{3}}{12}-\frac{3t(10t)^{3}}{12}$
$=326t^{4}$
$M$-図より$M_{max}=M(0)=-PL$
$\sigma_{zz}=\frac{M}{I}y$より
$\sigma_{zz}(y=-6t, z=0)=\frac{-PL}{326t^{4}}(-6t)=\frac{3PL}{163t^{3}}$
$\sigma_{zz}(y=6t, z=0)=\frac{-PL}{326t^{4}}(6t)=-\frac{3PL}{163t^{3}}$

おまけ

問2の先端のたわみを単位荷重法で求めてみる。
$0\le z\le L$では、
$M=P(z-L), \bar{M}=z-2L$
$L\le z\le 2L$では、
$M=0, \bar{M}=z-2L$
$EIv(2L)=\int_{0}^{2L}M\bar{M}dz$
$=\int_{0}^{L}P(z-L)(z-2L)dz+\int_{L}^{2L}0(z-2L)dz$
$=P[\frac{z^{3}}{3}-\frac{3L}{2}z^{2}+2L^{2}z]_{0}^{L}$
$=\frac{5}{6}PL^{3}$
$\therefore v(2L)=\frac{5PL^{3}}{6EI}$

メモ: