時間割_22前期†
↑キャンセル。受講できるか問い合わせたところ、教員免許の関係や実技をともなうため?私は受けられないらしい泣
ゼミ報告 or 自分用メモ†
点検と劣化診断
全部健全(ヤング10割)の振動数もグラフに入れる。
対数または多項式の回帰線を使う。
各箇所におけるヤング率と振動数の関係、どれも相関があって決定係数では感度を判定できない。
線形の回帰線の傾きの大きさで感度を評価することにする。
本当は線形でも対数でもなくもっといい感じの式があればいい。→多項式があった。
arch5の数値がちょっとおかしいので追計算
決定係数r^2で感度をみる
回帰線は線形?非線形?
かじか橋の回帰分析
しめくんにもデータ整理手伝ってもらうか
久保田
炭火焼 勇
MATLAB
かじかヤング0.9、0.8、0.7、...、0.1、0.05、0.02、0.01の12ケース×9箇所
自己交差
修士2年 4月†
22日
ベイズ推定の前に普通の回帰分析をしてみる
橋梁モニタリング
1日
今日からm2です。新しい気持ちでがんばりたい。
富山のげんき橋にとりかかる。
31日
拘束条件を剛結じゃなくしてみたら固有振動数どれくらい変わるかみてみたい。
明日から新学期。🌸
16日
金峰 水平の振動が実験と異なる。床版を等方性にするとどうなるか。(アスファルト舗装の影響など)
いろんな箇所を腐朽させて、それに対する振動数の変化をみる。局所の劣化から全体の剛性の推定。
ベイス推定。振動モードのパラメータ(橋全体)から局所劣化の推定。
11日
簡単なエラーを解消したり、容量の大きさによる不都合(メッシュのデータが壊れるなど)を経て、今日で腐朽を入れた解析をすることができた。
小さい部分での腐朽では、健全の状態と比べて、固有振動数はほとんど変わらなかった。
ねもとくん同様に、劣化においてどんな要因が固有振動数に影響を与えるのかを調べたい。
15日
↓腐朽部分をfuseせず、別でメッシュを切るとうまくいった。
14日
アーチに腐朽部分を作るためにグループ分けする。するとメッシュが切れずにsalomeが落ちてしまう。アーチの鋼材を細かく作った弊害か。
坊中橋(キングポストトラス、鋼補剛木桁)、元気橋(下路アーチ、富山)、みどり橋(頬杖ラーメン、長野)
2/6
確かめたいこと
・各部材のヤング率を、nastranの値と同じにして解析する
・もっと要素数を増やして振動数の減少率の低減(収束)を見たい
2/5
またmesh破損する。どうしたら防げる。
2/4
1/26のエラーは、支柱の一部で、meshのジオメトリのグループ作成をし忘れていた。
今はrunできていて要素数と振動数の収束をチェックしている。
2022年1月†
1/26
バイト後に寄る。
3Dと2D-1Dでメッシュ切ってもエラーだった泣 どうしたらいいの。
もどってアーチのみ、続いてアーチと水平支材で計算したら緑だった!
明日以降で部材増やしていってどこでエラーになるかをみつけよう。
明日は水の課題をする。
あしたあとrunする
geometry mesh asterstudy の、meshのデータが破損する泣
もっかいメッシュつくり直して計算するとメッシュ関連のエラー。
破損前はメッシュを3Dと1D-2D分けて切ったが、破損後は3D-2D-1Dで切った。
そのせいかなぁ。
1/11
メモ
残りの部材もつくる
緩衝ゴム、モルタルの物性値
床版のプレストレスの考慮、異方性
もしかしたら収束してない?メッシュもっと細かくするか
1/6
研究室初め。今年もよろしくお願いします。
12月†
12/18
支点4直る。コンパウンドはやはりできない(メッシュのエラー)
12/17
支点4がちょっとおかしい。一旦支点4抜いてコンパウンドしてメッシュ切る。
12/13
支柱に貼っつけてある鋼材は外す。アーチ端部のリブもいらない。
いまの日型の支柱は、底面でメッシュのエラーが出るのでひとまず日型もやめる。ただただ同じ断面の木材にする。
支柱の長さは、アーチ上面と床版下面の距離が変わらないようにする。木材長は実際よりも(もともとの鋼の接合部の分だけ)長くなる。
12/10
支柱1、2に水平材。支柱1、2は上半分くらい固い。
12/9
メッシュ
水平支材
12/5
支柱の高さがやはり合わないので、支柱の上につく横梁の高さで帳尻を合わせることにする。
11月†
11/29
支柱の高さが微妙に合わない→点で移動やfuseを試してみる。座標は見た目とやや異なることもある。
11日メモ
アーチ端部にもリブ入れる
支柱と鋼材
メモ
arch1 Shichu1(右側)
メモ
Box_4 tra_29 tra_31 tra_33 cut_5 tra_35 tra_36 Box_12 tra_42-44 shichu1 vertex_20
Box_12真ん中にもってく
10月†
10/25 [#t5f1f91e]
金峰アーチ1本を異方性をいれて振動解析。
弱方向ヤングは強方向の1/15。

| 水平1次 | 0.212Hz |
| 水平1/6くらいのところ | 0.431Hz |
| 水平2次 | 1.032Hz |
| 鉛直逆対称1次 | 1.363Hz |
10/11の等方性で解いたものと比べて1/5くらいになっている。
10/12
新しいpcにしてもらった!32GB!
メモ:メッシュ切り方
10/11
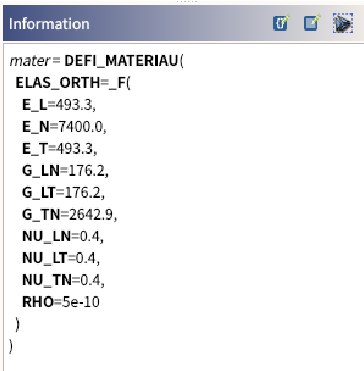
物性値
| ヤングMPa | ポアソン比 | 密度t/mm3 |
| 木 | 7400 | 0.4 | 5e-10 |
| 鋼 | 210000 | 0.3 | 7.8e-9 |
アーチ1本 固有振動数
| 水平対称1次 | 1.0383Hz |
| 水平逆対称1次 | 2.9136Hz |
| 鉛直逆対称1次 | 5.39879Hz |
| 水平対称2次 | 7.10924Hz |
| 鉛直対称1次 | 11.6456Hz |
10/18追記 ↑要素数748,439(メッシュ4)
金峰スギ、ヒノキ、イタジイ集成材
比重スギ0.38、ヒノキ0.41、シイノキ0.61
10/11追記。ヒンジは線をDX=DY=DZ=0。DRX=DRZ=Oは梁要素とか点のヒンジ。密度はt/mm3
10/7
基本的なことだが境界条件をヒンジにするやつがうまくいかない・・・
一応比較で、ぺったり面固定にしたら解ける。
あとmaterialに入れる物性値のスケールや単位が未だによく分かっていない。
金峰 まずはアーチだけで解けるかを確認していた。
いろいろエラーを経て振動モードの出力optionのBANDをPLUS_PETITEに変えたらうまくいった。(久しぶりの緑!)
なんでBANDがだめだったのかは不明。
10/6
Full job output should be available in the directory '/home/kouzou/ao_2021/kinpou_a_Files/RunCase_1/Result-Stage_1/logs'.
Error during the dynamic allocation. It was not possible to allocate
a memory zone length 1037913 Mo, one exceeds the maximum limit
built-in with 1428 Mo and one occupies already 102 Mo.
The last operation of memory deallocation made it possible to recover 5 Mo.
10/4 ヤング率低減の他に接合の条件の緩和(?)の検討
それをどうやって表現するか
アーチ異方性
きょくしょけい
極座標
断面2次モーメントとEIを計算しました.E木=7.4GPa(スギ),E鋼=205GPa
以下計算したEIです.
①木部材のみ→ 0.466 GPa・m^4(ギガとかミリの書き方は一般にこれで合っていますか?)
②木+鋼板→ 1.41 GPa・m^4
③鋼板のみ→ 0.98 GPa・m^4
④鋼板+鋼リブ→ 3.52 GPa・m^4
リブありのEIが大きく見えますが,これはどう評価しましょう(未だにこの辺の感覚がわからないです泣)
やはりリブも,細かいけどちゃんと作った方がいい気がする.
アーチリブの図面写真をこのページの下の方に載せました.(図面ってネットにアップしても大丈夫ですか?)
リブの棚の部分はモデル簡素化のため省略する方向.
棚の有無でEIがどれだけ変わるか計算する.
省略する場合,棚130mmとクリアランス5mmの和の135mmの隙間があく.
あ,スカーラップ(穴)を作っていなかった.
穴の寸法が図面に載っていないかもしれない.そんなことはあるか?
アーチリブを作った.
ボルトの固定は,goemetryでは省略してよいか?
金峰のモデルちょこっと作ってます.
木材発表の図表なるはやで.
かじか橋 5番目のアーチ端部 ドライバーが4cm程刺さるくらいぐじゅぐじゅ(及川さん)
ねもと君と共有
かじか橋について,本田先生の研究,アーチ橋,今後 部材ごとの劣化の影響
厳密解(理論解)と近似解.
引張→1次要素で厳密解を含む.曲げ→2次要素で厳密解を含む.せん断→2次要素でも厳密解を含まない(近似解.)
高性能要素
a. Wilson-Taylor の非適合要素(QM6):内部自由度追加
b. Simo-Rifaiの拡張ひずみ要素(EAS):内部自由度追加
c. u-p混合法要素(複数種類あり)
d. 次数低減積分+アワーグラス制御:1点積分
e. B-bar要素(選択的次数低減要素):ある種の混合法要素と等価
6/1
オイラー梁要素(POU_D_E)→せん断変形を考慮しない.
ティモシェンコ梁要素(POU_D_T)→せん断変形を考慮する.
1次ティモシェンコ梁要素→ロッキング現象
シェル要素→キルヒホッフラブ→(緩和)離散キルヒホッフ(せん断変形を考慮しない),退化シェル要素(梁要素でいうティモシェンコ理論に相当.せん断変形を考慮するためある程度の厚みを許容する.)
5/31
ソリッド要素で全体解析をするのはなぜ? ー (今までは一様にヤング率を低下させているが)部材ごとの腐朽に合わせてヤング率を入力できるため.
かじか橋の振動解析で,梁要素の精度が落ちたのはなぜ? ー 原因のひとつに,アーチを等方性で解いたから(曲がっているアーチに異方性を入れるのは難しい.)
梁要素とシェル要素はせん断変形を考慮しない?ティモシェンコ梁要素はせん断変形を考慮する.
木材は縦横でヤング率が大きく異なる異方性材料.せん断弾性係数は小さい.そのため佐々木さんの卒論なども(等方性で解いていたが)異方性で解いてみるべき.
梁要素に異方性
5/28
シェル要素のメッシュ分割は,2次要素ではできなかった.
5/27
実寸のメッシュ長さと,Salomeでメッシュ切った図を入れる.
シェル要素の収束の図を入れる.
シェル要素を2次要素で解いた場合,結果を差し替える.
佐々木さんのやり直しについて,「部材長:部材幅」が具体的にいくつ程になると梁要素の解析値に誤差が出始めるか,ねもと君に調べてもらおう.
片持梁,両端支持アーチ,ラーメン,etc.
5/26
かじか橋 床版のシェル要素を粗いメッシュで2次要素でといてみる.
結果がどのくらい変わるか(変わらないか.)
5/24
今までの立体要素の解析(佐々木さんの卒論やかじか橋の解析)を,
メッシュ分割を四面体2次要素や六面体要素にしてやり直してみたい.
俺の修論は金峰2000年橋で,ねもと君の卒論はかじか橋の解析精度改良,という案.
(ねもと君に↑のやり直しをやってもらうか?)
金峰のモデル作成途中.
木材発表の準備.データ整理したい.
木材発表の準備.
図を貼っておおまかな流れを確認(5月末まで)
6月中は文章の推敲.
金峰2000年橋をsalomeでモデル化したい.
図面は研究室のそのへんにある.(あった)
ネットで調べたり本田先生に直接連絡をとって固有振動数のデータなどを入手する.
- 今のモデルを、より精度良く解析することを検討
- 「梁要素のほうが固くなるはず」のチェック
- 他の橋をモデル化して同様の比較をする
- 木橋の耐用年数の一助
- ねもとくんと情報共有
かじか橋†

感度の棒グラフ†
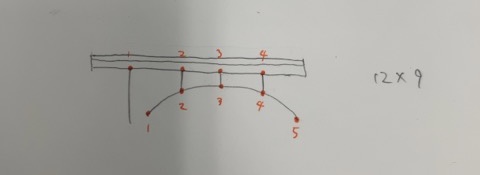
アーチ†
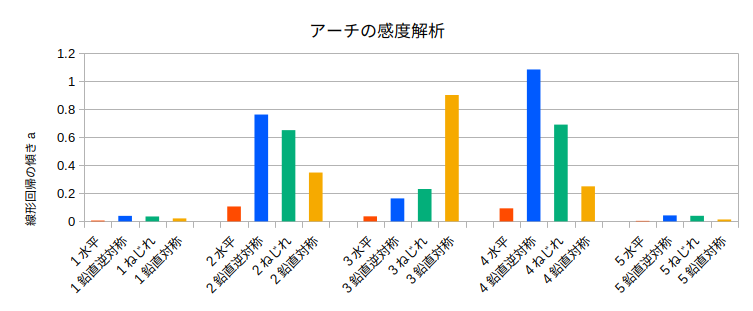
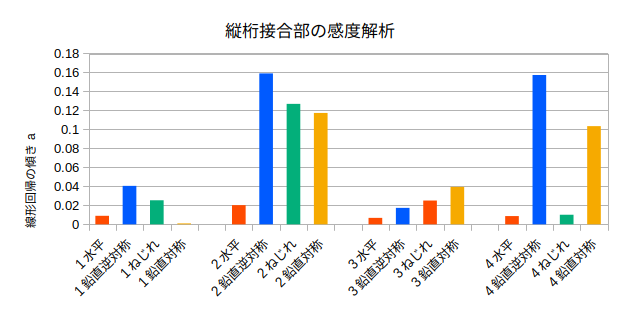
アーチ1の腐朽†
どのモードも同じような低減のしかたである。
水平1次モード†
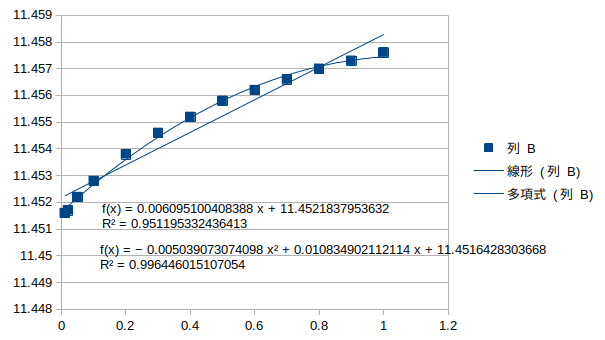
鉛直逆対称1次モード†
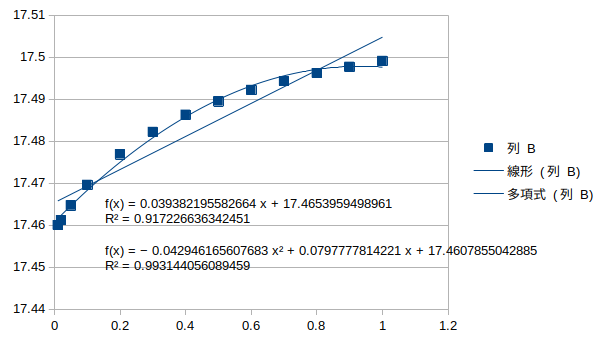
ねじれ逆対称1次モード†
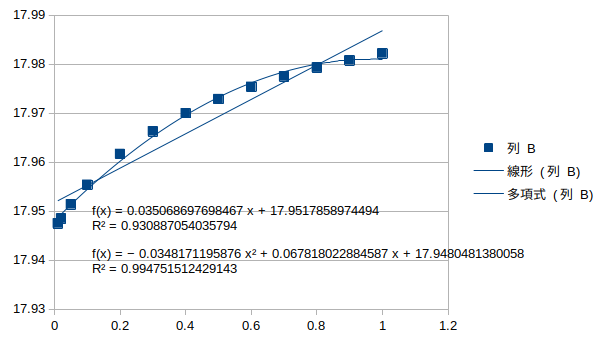
鉛直対称1次モード†
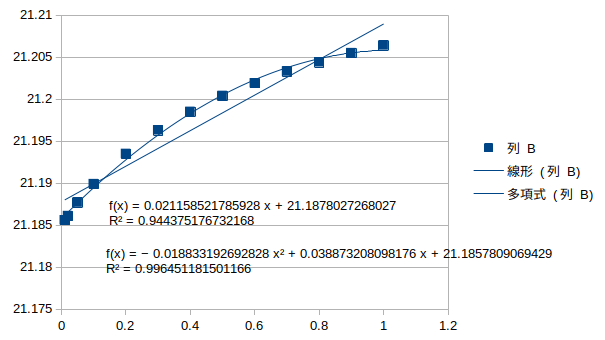
アーチ2の腐朽†
水平1次モード†
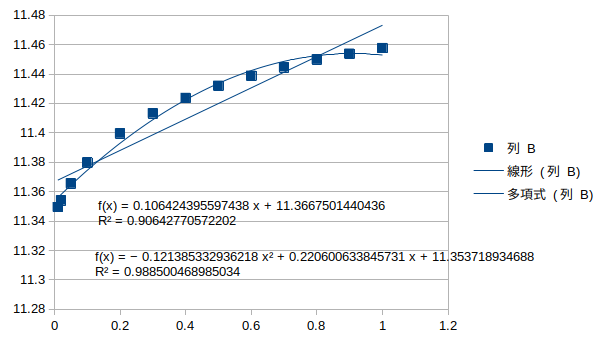
鉛直逆対称1次モード†
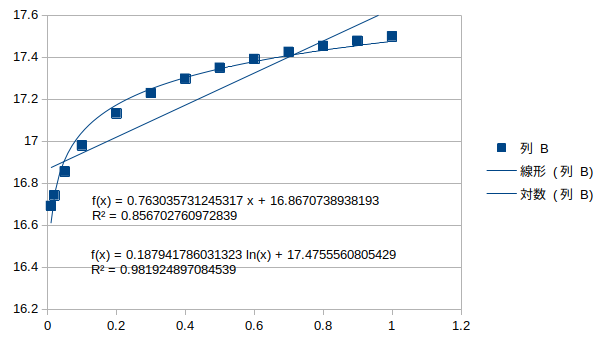
ねじれ逆対称1次モード†

鉛直対称1次モード†
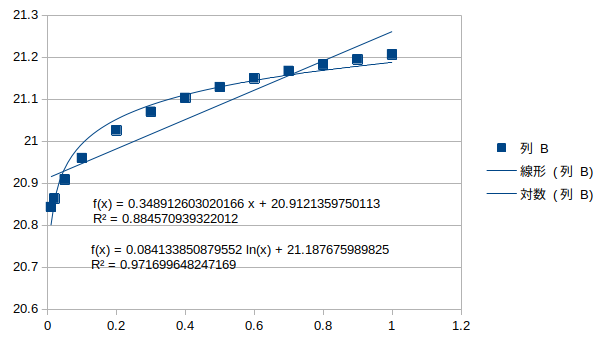
アーチ3の腐朽†
水平1次モード†
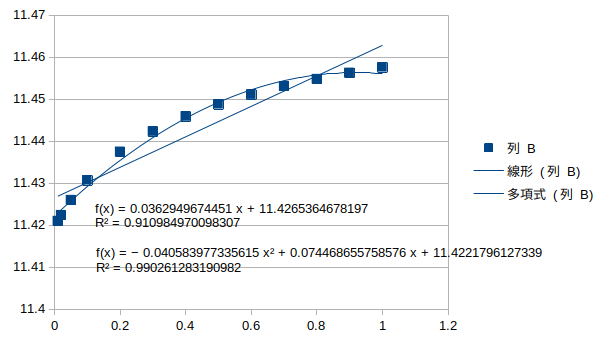
鉛直逆対称1次モード†
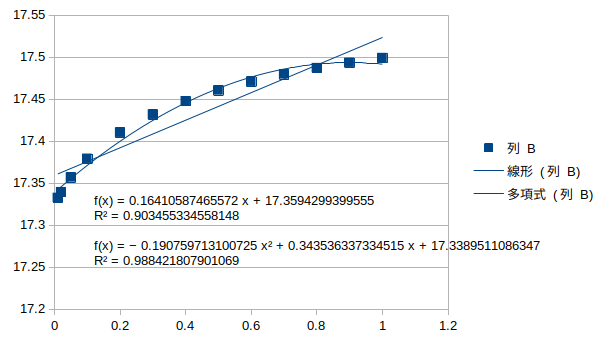
ねじれ逆対称1次モード†
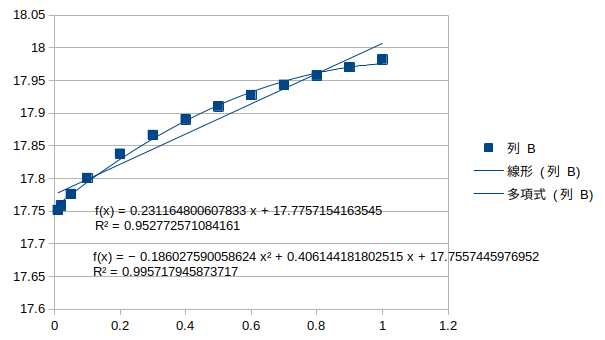
鉛直対称1次モード†
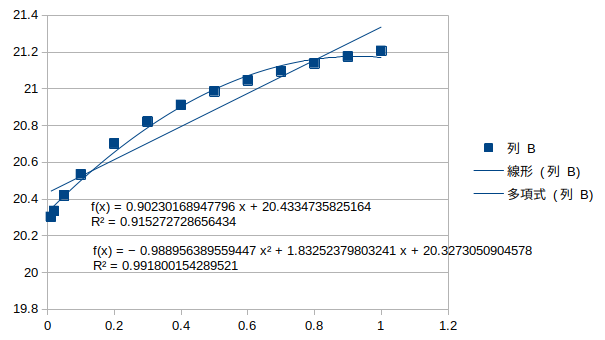
アーチ4の腐朽†
水平1次モード†
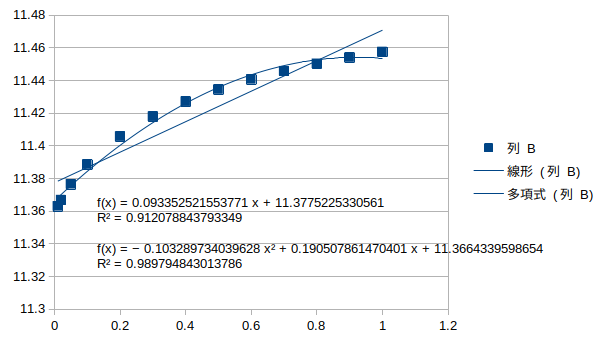
鉛直逆対称1次モード†
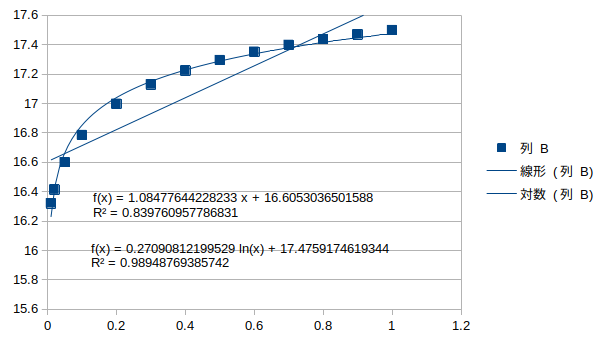
ねじれ逆対称1次モード†
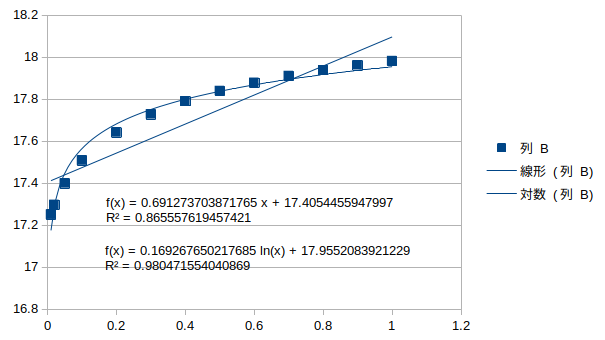
鉛直対称1次モード†
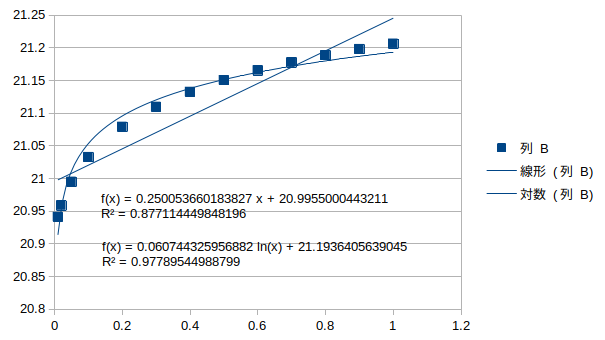
アーチ5の腐朽†
水平1次モード†
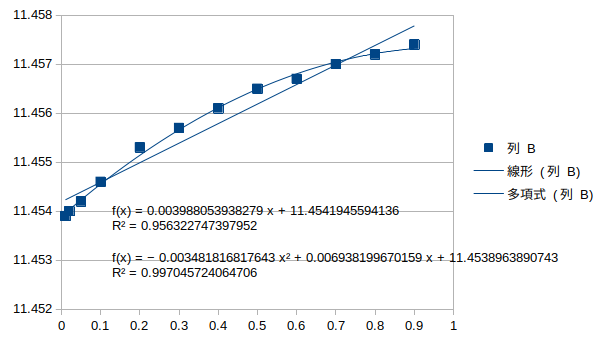
鉛直逆対称1次モード†
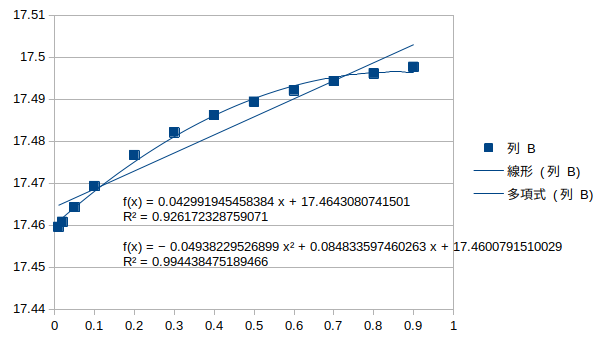
ねじれ逆対称1次モード†
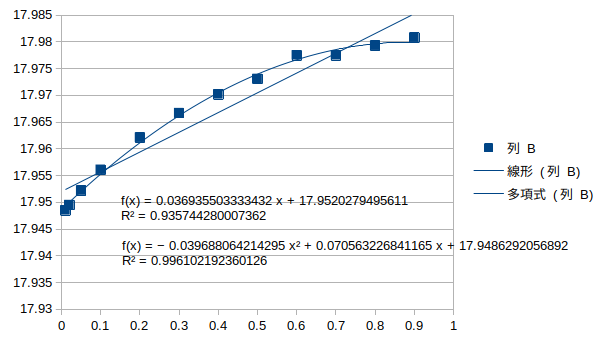
鉛直対称1次モード†
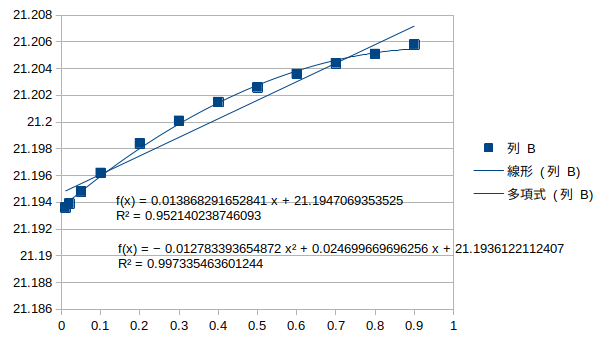
縦桁1の腐朽†
対数回帰とよく一致している。
水平1次モード†
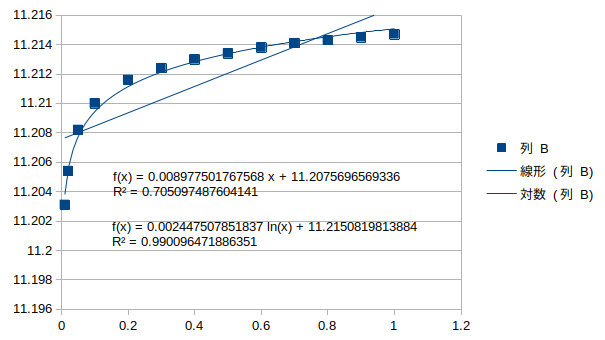
鉛直逆対称1次モード†
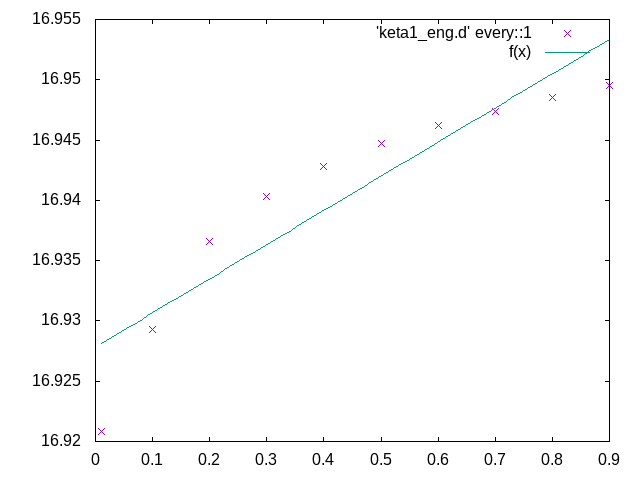
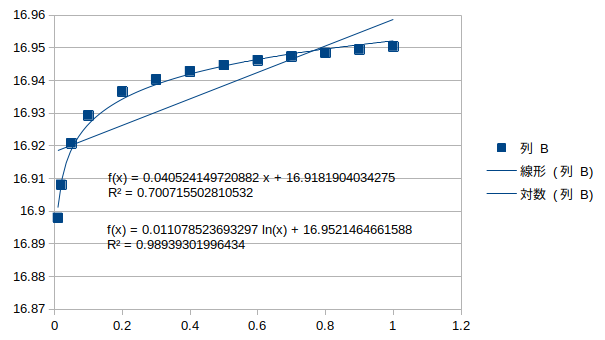
ねじれ逆対称1次モード†
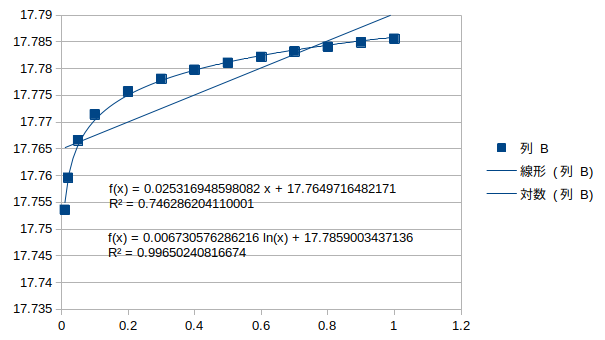
鉛直対称1次モード†
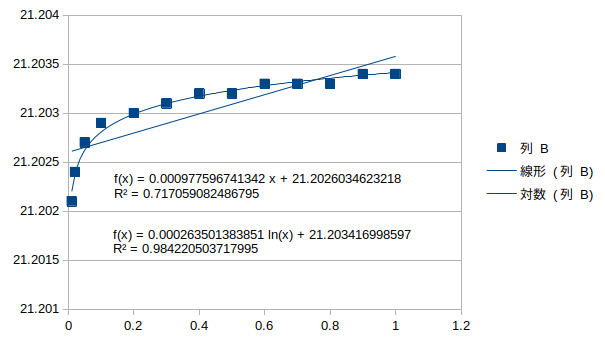
縦桁2の腐朽†
水平1次モード†
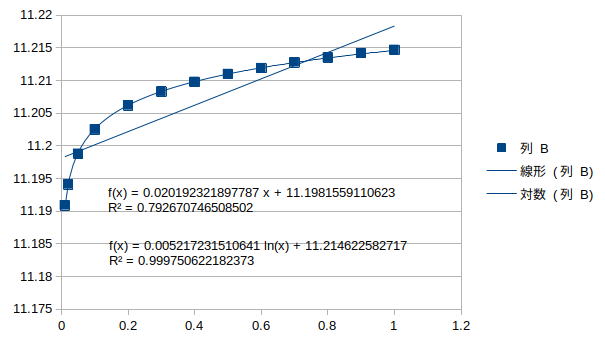
鉛直逆対称1次モード†

ねじれ逆対称1次モード†
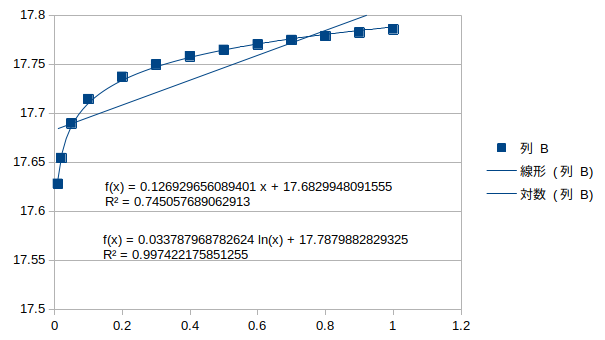
鉛直対称1次モード†
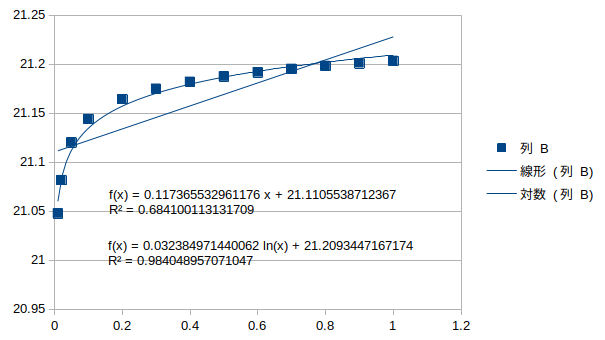
縦桁3の腐朽†
水平1次モード†
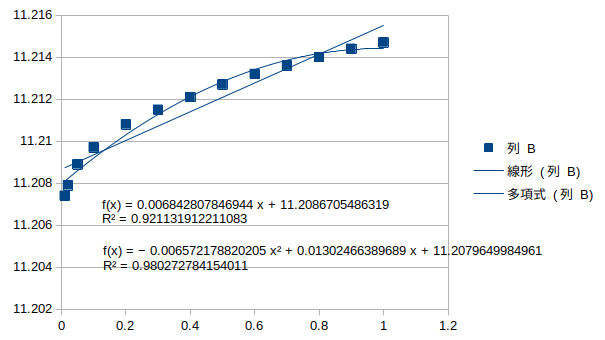
鉛直逆対称1次モード†
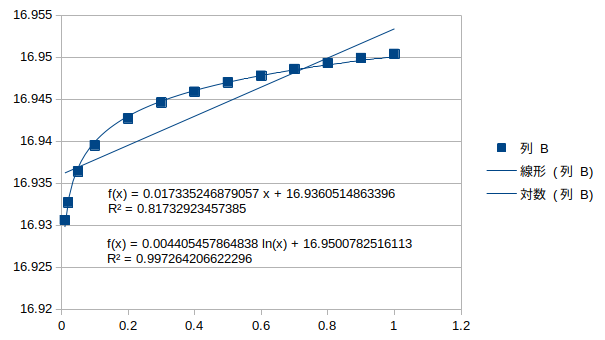
ねじれ逆対称1次モード†
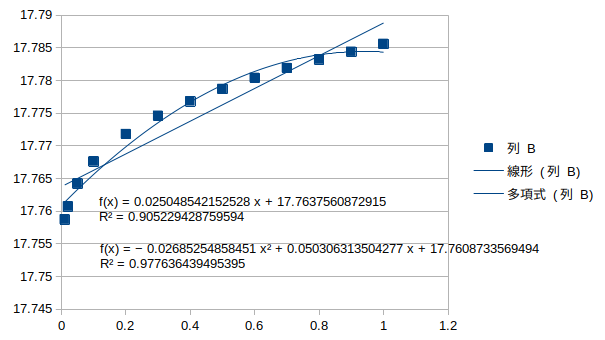
鉛直対称1次モード†
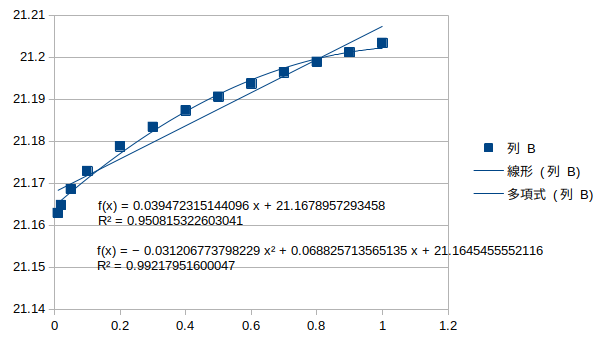
縦桁4の腐朽†
水平1次モード†
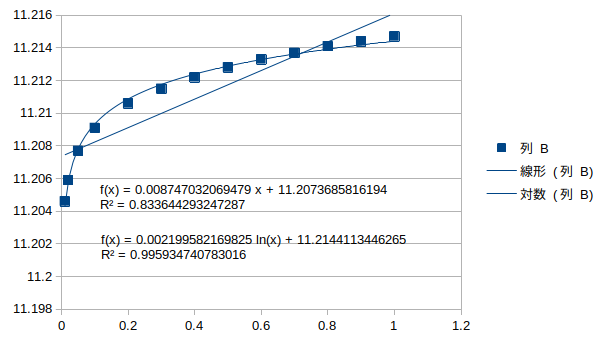
鉛直逆対称1次モード†
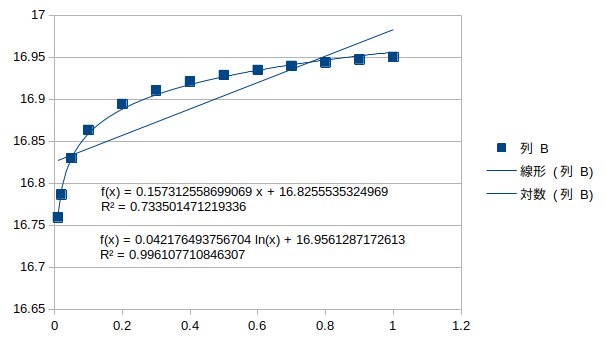
ねじれ逆対称1次モード†
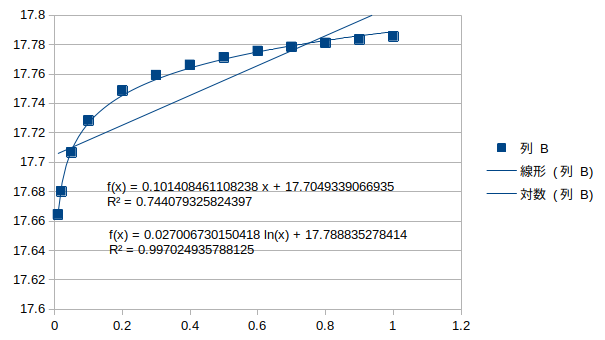
鉛直対称1次モード†
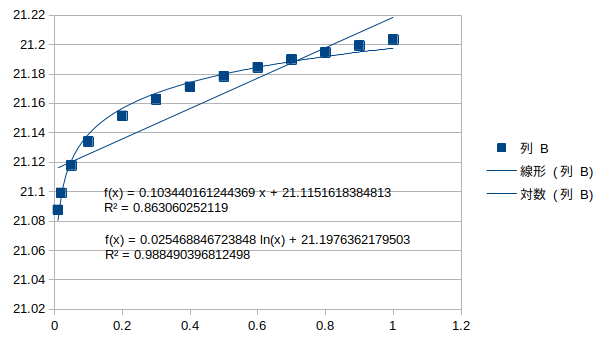
回帰分析のための解析データ進捗†

| 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | 0.05 | 0.02 | 0.01 |
| from_akesson1 | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ |
| from_akesson2 | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ |
| from_akesson3 | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ |
| from_akesson4 | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ |
| from_akesson5 | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ |
| ketafukyu1 | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ |
| ketafukyu2 | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ |
| ketafukyu3 | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ |
| ketafukyu4 | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ | ○ |
データ整理進捗†
| 水平1次 | 鉛直逆対称1次 | ねじれ逆対称 | 鉛直対称1次 |
| arch1 | ○ | ○ | ○ | ○ |
| arch2 | ○ | ○ | ○ | ○ |
| arch3 | ○ | ○ | ○ | ○ |
| arch4 | ○ | ○ | ○ | ○ |
| arch5 | ○ | ○ | ○ | ○ |
| keta1 | ○ | ○ | ○ | ○ |
| keta2 | ○ | ○ | ○ | ○ |
| keta3 | ○ | ○ | ○ | ○ |
| keta4 | ○ | ○ | ○ | ○ |
げんき橋†

↑福岡大学木橋資料館より
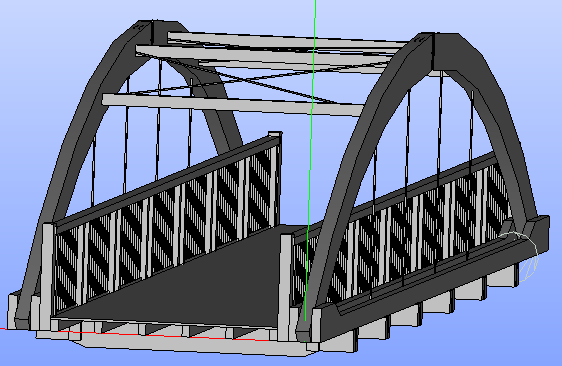
5/12†
振動モードも固有振動数もsalomeと実験でまったく合わない泣
本田先生のnastranと実験はよく合っている。
金峰2000年橋 振動解析†
モデル作成中・・・ →2021/12 概形が完成→ 2022/1/26 横構と水平材を加えて完成

↑福岡大学木橋資料館より
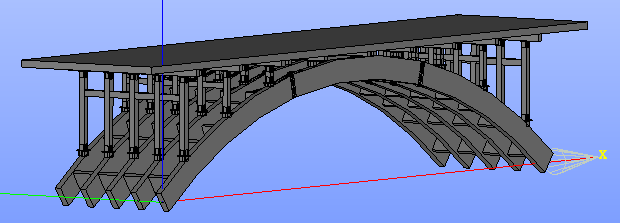
平成30年の調査(金沢工大)の測定値†
| | H12年 | H30年 |
| 鉛直逆対称1次 | 4.00Hz | 3.71Hz(-7.25%) |
| 水平1次 | 4.69Hz | 4.49Hz(-4.26%) |
| ねじれ逆対称1次 | 5.47Hz | 5.37Hz(-1.83%) |
| 鉛直対称1次 | 5.86Hz | 5.71Hz(-2.56%) |
- 20年弱経過しても固有振動数の低下は小さい。
- 目視でも局所的な劣化はほとんど見られなかったそうだ。
- Nastranで測定値と解析値の固有振動数を一致させる逆解析をしたところ、ヤング率の低減が10%だったそうだ。
アスファルト舗装を考慮したら実験と解析で振動モード合うか?†
| | 解析アスファルトあり | 解析アスファルトなし | H12年測定値 |
| 鉛直逆対称1次 | 4.46Hz | 4.08Hz | 4.00Hz |
| 水平1次 | 4.20Hz | 3.28Hz | 4.69Hz |
| ねじれ逆対称1次 | 7.53Hz | 7.98Hz | 5.47Hz |
| 鉛直対称1次 | 5.80Hz | 6.12Hz | 5.86Hz |
- アスファルト舗装を考慮しても振動モード一致しない。
- アスファルトは厚さ10mmで床版に剛結、ヤング率5GPa、ポアソン比0.35、密度2.35e-9tf/mm3
まずは極端に横材すべてのヤング率を1/100にしてみた†
| | salome健全 | 17%一様に低減 | 横材1/100 |
| 水平1次 | 3.28Hz | 3.01Hz | 2.43Hz |
| 鉛直逆対称1次 | 4.08Hz | 3.76Hz | 3.71Hz |
| 鉛直対称1次 | 6.12Hz | 5.60Hz | 5.68Hz |
| ねじれ逆対称1次 | 7.98Hz | 7.31Hz | 7.39Hz |
| 鉛直対称2次 | 9.11Hz | 8.32Hz | 8.32Hz |
- 17%低減と横材1/100を比べると、水平1次の他の振動モードは大体近い値になった。(誤差数%程度)
- 横材ヤング1/100では特に水平1次の振動数が小さくなった(17%低減との誤差20%程度)ため、横材の腐朽は水平1次の振動数に影響を与えるといえるかもしれない。
- 逆もそう。水平1次モードの振動数の低減は横材の腐朽によるものといえるかもしれない。
Nastranと同じ物性値で床版等方性†
| | salome | Nastran | H12測定値 |
| 鉛直逆対称1次 | 6.56Hz(64.0%) | 3.91Hz(-2.25%) | 4.00Hz |
| 水平1次 | - | 4.78Hz(1.92%) | 4.69Hz |
| ねじれ逆対称1次 | 8.82Hz(64.2%) | 5.47(0%) | 5.47Hz |
| 鉛直対称1次 | 7.37Hz(25.8%) | 5.63Hz(-3.92%) | 5.86Hz |
| 鉛直対称2次 | 9.89Hz(16.4%) | 8.53Hz(0.353%) | 8.50Hz |
- Nastranは測定値とよく合うが、salomeは測定値ともNastranともずれる。
- 水平の振動は出ず。ねじれ逆対称1次は相変わらず鉛直対称1次よりも高い周波数。
3/16 salomeヤング率一様に低減†
| | ヤング率0%低減 | 10%低減 | 15%低減 | 17%低減 |
| 水平1次 | 3.28Hz | 3.12Hz(-4.88%) | 3.04Hz(-7.32%) | 3.01Hz(-8.23%) |
| 鉛直逆対称1次 | 4.08Hz | 3.89(-4.66%) | 3.80Hz(-6.86%) | 3.76Hz(-7.84%) |
| 鉛直対称1次 | 6.12Hz | 5.82Hz(-4.90%) | 5.66Hz(-7.52%) | 5.60Hz(-8.50%) |
| ねじれ対称1次 | 7.98Hz | 7.60Hz(-4.76%) | 7.39Hz(-7.39%) | 7.31Hz(-8.40%) |
| 鉛直対称2次 | 9.11Hz | 8.66Hz(-4.94%) | 8.42Hz(-7.57%) | 8.32Hz(-8.67%) |
- 測定値について、18年の経過で鉛直逆対称1次の振動数が7.25%低減しているため、解析でも鉛直逆対称1次の振動数が7.25%低減するまでヤング率をさげてみる。
- 水平1次の振動数が実験値よりも小さい。
- ねじれ逆対称1次の振動数が実験値よりも大きい。
- Nastranは実験値と解析値でよく対応している。
- 各モードの経年による振動数の低減率が、実験値ではそれぞれ異なるのに対し、ヤング率を一様に低減した場合のsalomeの解析値はそれぞれ同じような低減率の値になる。
3/11 アーチ支柱接合部50mm腐朽†
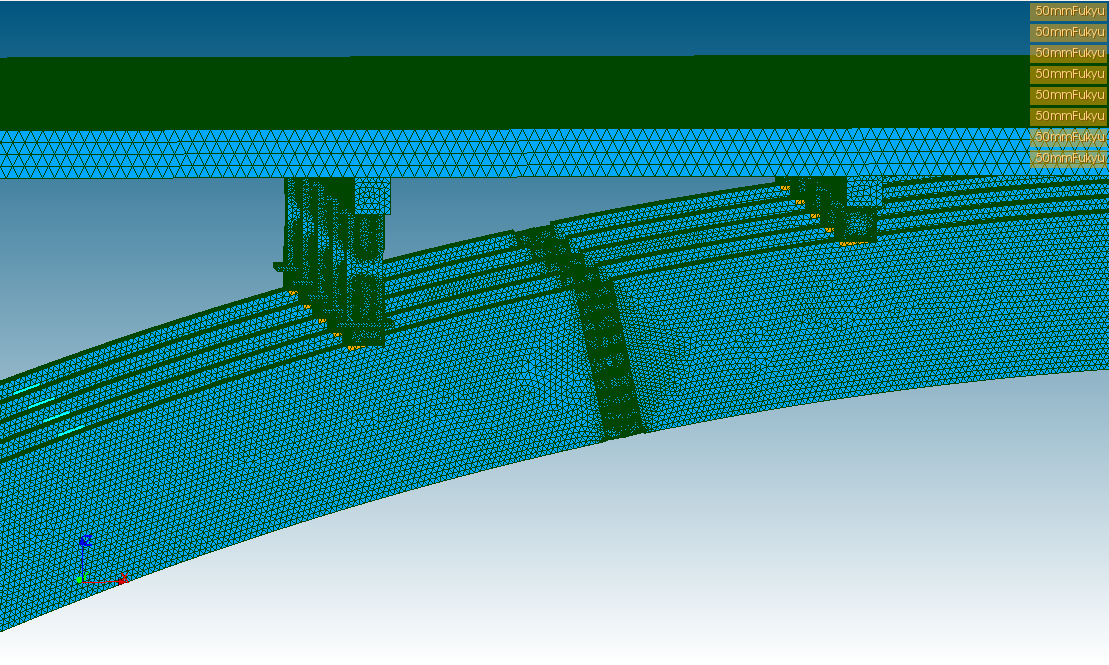
- アーチの頭頂部(クラウン)を除く8箇所の接合部を深さ50mmだけ腐朽させた。(オレンジ色)
- 腐朽箇所はヤング率を1/100にすることで表現。
- 15,680,098要素
- 下の表に解析結果。かっこ内は2/10の要素数15,644,607腐朽なしとの誤差。
| | 50mm腐朽(1568万要素) | 腐朽なし(1564万要素) |
| 水平1次 | 3.26Hz(-0.61%) | 3.28Hz |
| 鉛直逆対称1次 | 4.05Hz(-0.74%) | 4.08Hz |
| 鉛直対称1次 | 6.08Hz(-0.65%) | 6.12Hz |
| ねじれ逆対称1次 | - | 7.98Hz |
| 鉛直対称2次 | 9.08Hz(-0.33%) | 9.11Hz |
- ねもとくんの研究の通り、50mm程度の腐朽では固有振動数にそんなに影響は出ない。
2/5-10 収束のグラフ†
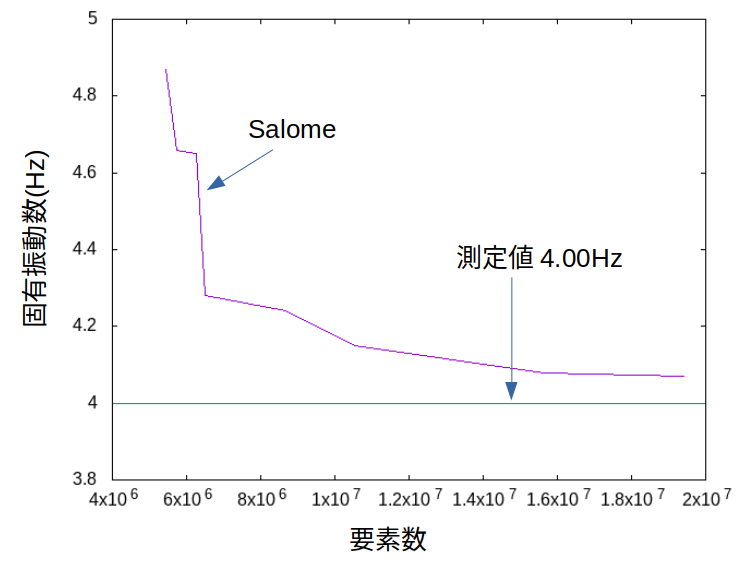
- 2/4のデータに加えて、要素数15,644,607と19,421,036でも解析ができたのでそれを加えて図を作成。
- 測定値に近づいて収束した。
- 下の表は要素数15,644,607の解析値と、測定値、Nastranの解析値の比較。かっこ内はsalomeの測定値に対する相対誤差。
| | salome(1564万要素) | 実験値(砂袋落下) | Nastran |
| 水平1次 | 3.30Hz(-29.6%) | 4.69Hz | 4.78Hz |
| 鉛直逆対称1次 | 4.08Hz(2.0%) | 4.00Hz | 3.91Hz |
| 鉛直対称1次 | 6.12Hz(4.4%) | 5.86Hz | 5.63Hz |
| 鉛直対称2次 | 9.11Hz(7.2%) | 8.50Hz | 8.53Hz |
- 今後の小さい目標は、
- ①いったんパソコンの限界まで要素数を上げてみたい。→2,500万要素くらいだとメモリのエラーが出た。2,000万要素くらいが上限か。
- ②部材ごとのヤング率を、Nastranで入れたものと同じにして結果がどうなるかを見たい。→鉛直逆対称、鉛直対称のモードは有効数字3桁までで同じ値になった。水平1次は0.02Hzだけ小さくなった(誤差-0.61%)
- ③メッシュを2次要素で切るとどうなるかを見たい。
- 以上を確認したら、ねもと君のように部材の腐朽・欠損による振動数の影響をみる。
- その後はまた別の橋で同様の振動解析。
2/4 要素数による振動数の収束をチェック†

- アーチと床版、特に床版のメッシュ細かさが影響大
- 床版は異方性を入れて他の部材より柔らかくなってるからメッシュを細かくすると振動数落ちやすか?
- 写真はいったん今日までの分だが、パソコンの容量的にもう少し要素数を増やせそうなので今後もっと要素数増やして確認したい
1/24 床版に異方性を入れる†
- 床版に異方性を入れたら振動数は大きく落ち、振動モードも水平が現れるなど大きな変化があった。
- 床版 EN=7.65GPa、EL=ET=1/20=0.3825GPa、GLN=GLT=GTN=1/15=510GPa、NU=0.016、RHO=8.163e-10
| | salome(1/24) | 実験値(砂袋落下) | Nastran |
| 水平1次 | 3.89Hz | 4.69Hz | 4.78Hz |
| 鉛直逆対称1次 | 4.86Hz | 4.00Hz | 3.91Hz |
| 鉛直対称1次 | 7.12Hz | 5.86Hz | 5.63Hz |
| ねじれ対称1次? | 9.15Hz | 5.47Hz | 5.47Hz |
| 鉛直対称2次 | 10.43Hz | 8.50Hz | 8.53Hz |
- 水平が出たのはいいが、salomeは水平1次と鉛直逆対称1次では水平1次が小さいのに対し、実験値とNastranは鉛直逆対称1次のほうが小さい。
- いまメッシュが1次要素で120万要素くらい。もっとメッシュを細かくしたり2次要素にしたりすればsalomeの振動数や振動モードも実験値に近づくのではないか。
- ちなみに床版のほかの木部材は、nastranではそれぞれ異なる物性値が入ってますが、今回は省略して床版軸方向と同じ7.65GPaで統一してます。面倒がってすみません。比重も0.8163で木は全部同じです。
1/7 1/6の続き†
- 1/6の設定は本田先生の測定値と比べてsalomeの固有振動数が2倍くらい大きい。
- 測定値に近づける(やわらかくする)ため、いったん鋼材部分も木材と同じヤング率、ポアソン比、密度を入れてみた。
| | 全部木(1/7) | 木・鋼(1/6) | 実験値(砂袋落下) | Nastran |
| 鉛直逆対称1次 | 8.06Hz | 9.35Hz | 4.00Hz | 3.91Hz |
| 鉛直対称1次 | 9.56Hz | 10.65Hz | 5.86Hz | 5.63Hz |
| 鉛直対称2次 | 13.52Hz | 14.34Hz | 8.50Hz | 8.53Hz |
- あんまり振動数落ちない。
2022/1/6 アーチ、水平支材、支柱、横梁、床版†

- 床版と横梁くっつく。木のヤング率は7.4GPa、床版もいったん同じ。
- 水平の振動が出なかった。本田先生の実験では水平の振動も測定されている。
| | Salome | 実験値(砂袋落下) | Nastran |
| 鉛直逆対称1次 | 9.35Hz | 4.00Hz | 3.91Hz |
| 鉛直対称1次 | 10.65Hz | 5.86Hz | 5.63Hz |
| 鉛直対称2次 | 14.34Hz | 8.50Hz | 8.53Hz |
12/25 アーチ、水平支材、支柱、横梁、床版†

12/24 アーチ、水平支材、支柱、横梁†

12/22 アーチ、水平支材、支柱†

| 水平1次 | 3.96Hz |
| 鉛直逆対称1次 | 4.43Hz |
| 鉛直対称1次 | 10.52Hz |
12/13†
geometry
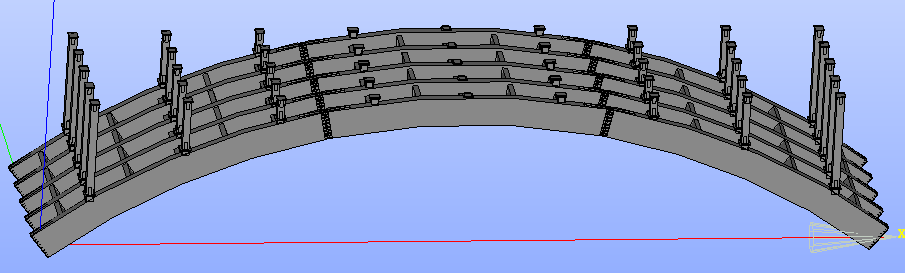
- 支柱の高さのずれは、支柱と床版の間にある横梁の高さを調節することで補正する。
- 見落としていたが、アーチ端部にも補剛リブがあった。それを作ってアーチ部材のみでメッシュを切ろうとするも、切れず。
エラーの内容は要素数の問題ではなく、接点や面の共有がうまくいっていないような内容のため、工夫すればエラーはとれそう。
- 支柱1本ずつではメッシュが切れるが支柱全体でコンパウンドするとメッシュが切れない(エラーが出る。)

- 端部に補剛リブの無いアーチとアーチ間をつなぐ水平支材のみではメッシュは切れてAsterStudyのRunも緑だった。(ひとつ上のモデル)
- 参考程度に解析の固有振動数を下に載せる。木材7.4GPa。実際はアーチ端部に補剛リブがある。またメッシュの細かさも、てきとう。
| 水平1次 | 4.14Hz |
| 鉛直逆対称1次 | 4.84Hz |
| 鉛直対称1次 | 10.53Hz |
| 鉛直対称2次 | 17.47Hz |
創造工房†
2材料†
歌など†
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
