皆川の卒論日誌の履歴(No.37)

卒論
- テーマ
- 参考資料
解析モデルと結果
創造工房実習

卒論†

テーマ†

ケーブルの腐食やクラックを考慮した固有振動解析（皆川）

   昨年度の山本の研究の続き．ケーブルの腐食方法やimpactの与え方などを変化させる．できればクラックやサグの解析も検討する（参考資料あり）
   昨年できなかった130mくらいの長いケーブルを要素分割し，衝撃を与えて，その固有振動モードや振動解析を行う．サグは新しく挑戦

↑

参考資料†

・山本さんの卒論

ケーブル腐食をくり抜くことで再現
腐食の長さ・深さ・位置を変えて解析

・角田さんの修論

健全モデルと腐食モデルを使って、ケーブル破断時の連鎖崩壊挙動
C1~C14をそれぞれ破断させた時に崩壊するかの解析
ケーブル健全時・腐食時の動的増幅率(DAF)と荷重再分配率(LRR)の検討

↑

解析モデルと結果†

↑

長さ1000mm、半径0.5mmの健全モデル†

固定の仕方を線固定にした。(張力は面載荷で与えた。)

固有振動数の理論値 f=6.37Hz 　解析時間0〜30秒　細長比3544.91

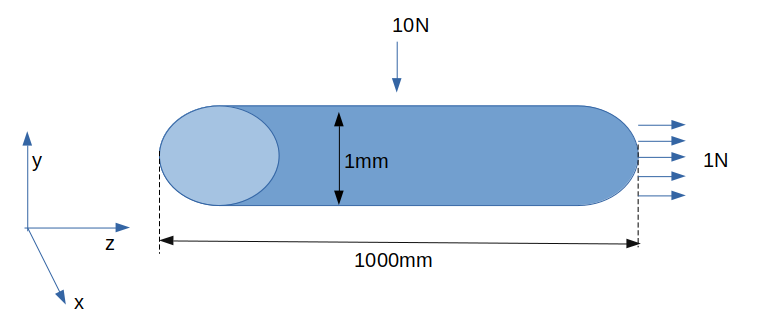
時間	行うこと
0〜5秒	張力(1N)をかける。
5〜14.99秒	ケーブルを安定させる。
15秒	10Nの力を与える。
15.01〜30秒	卓越した振動を検出する。

↑

由利橋のケーブル　長さ71000mm、半径157.5mmの健全モデルにインパクトを与える†

固有振動数の理論値 f=2.85Hz 　解析時間0〜100秒　細長比251.7

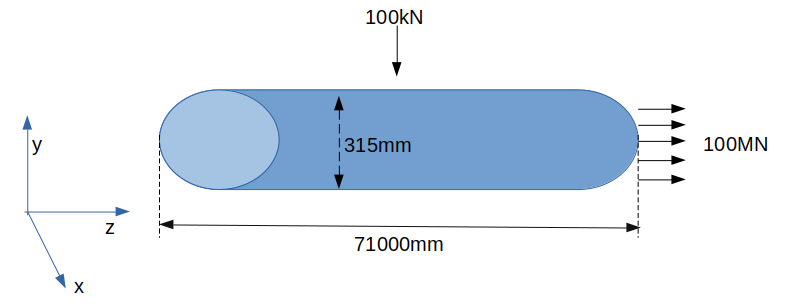
時間	行うこと
0〜5秒	張力(100MN)をかける。
5〜14.99秒	ケーブルを安定させる。
15秒	100kNの力を与える。
15.01〜100秒	卓越した振動を検出する。

結果
Mesh50 ボリューム169538
中央部の振動数

波形を書かせるとおかしな波形となり、モードの推定ができなくなってしまった。

↑

6/24 内部張力が、与えている張力と等しいかの解析†

中央部(point35500)と張力を与えた部分(point71000)の15秒〜100秒の主応力の平均値、最大値、最小値を調べた。
中央部(point35500)
平均値99.6MN 最大値104.5MN 最小値98.7MN
張力を与えた部分(point71000)
平均値・最大値・最小値ともに95.6MN

↑

インパクト1000kNに変更†

上の解析のインパクトを100kN→1000kNに変更して解析を行った。
インパクトを与えた後(16.20s)の100kNの時のモードと1000kNの時のモードを表したものが下の画像である。(1000倍)

↑

6/21 張力とインパクトをいろいろ変えて解析†

①張力100MN、インパクト100kN
②張力100MN、インパクト1000kN
③張力200MN、インパクト100kN
④張力200MN、インパクト1000kN
どの解析でも下のような同じ振動数が出力された。

↑

由利橋のケーブル(長さ71000mm、半径157.5mm)に振動を与える解析†

↑

両端に振動を与える解析†

両端に理論値である2.85Hzの振動を与える解析
ParaVISでモードを見ると下のようになり、微細な振動は見られたが大きな振動は見られなかった。
両端を固定しており、その部分に振動を入れているからだと思う。

↑

中心に振動を与える解析†

長さ71000mm、張力100MNの弦の理論値である2.85Hzを中心の点に与えて解析を行った。
モードは以下のようになった。
振動を与えた後
16.41秒

16.58秒

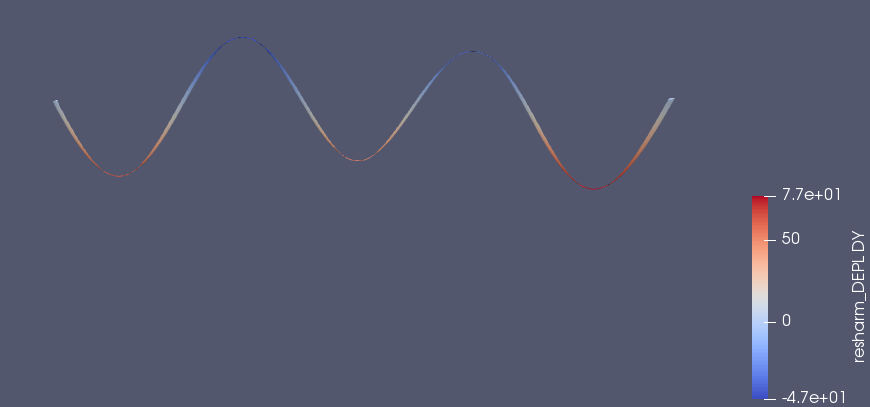
17.94秒

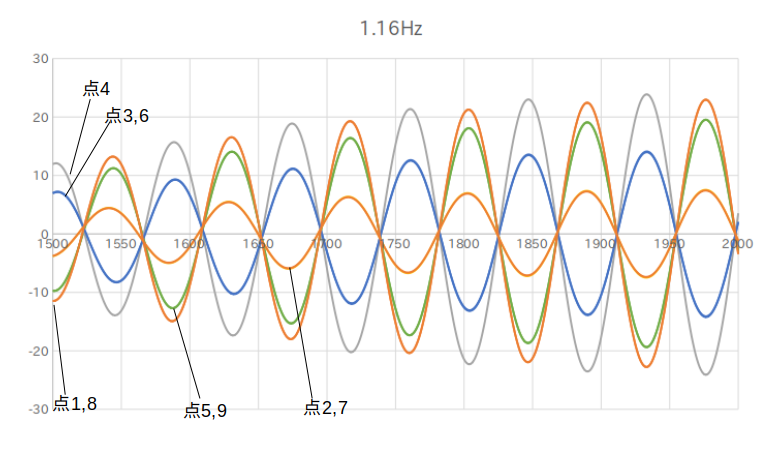
中心に1.16Hzの振動を与える解析を行った。

振動を与える直前(14.99秒)

振動を与えた直後(15.5秒)

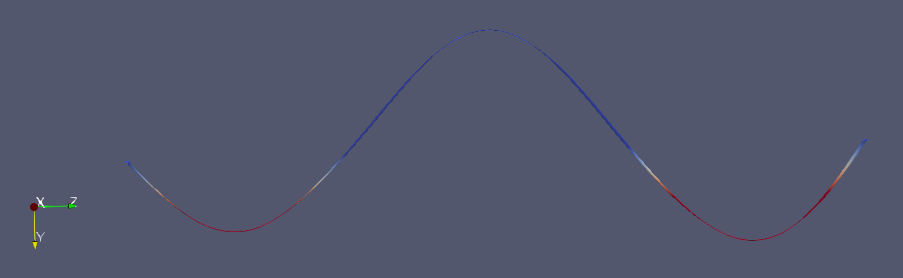
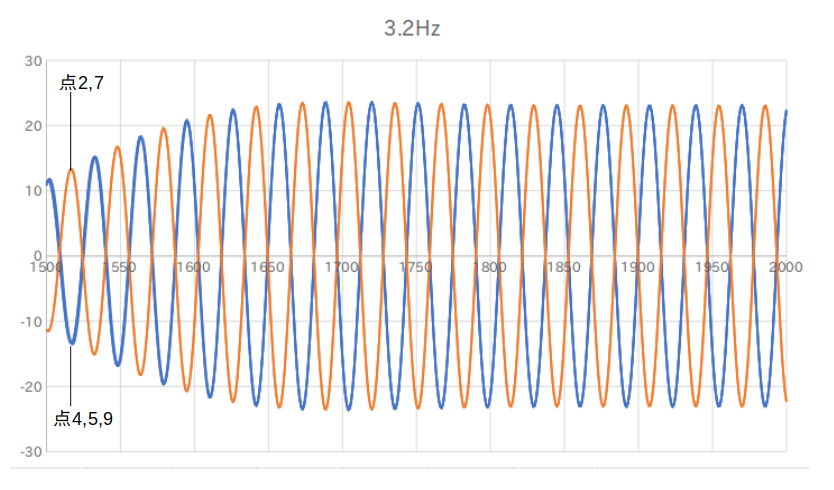
中心に3.2Hzの振動を与える解析を行った。~ [#t2afbbe4] 振動を与える直前(14.99秒)

振動を与えた後は下の2つの位相が繰り返された。

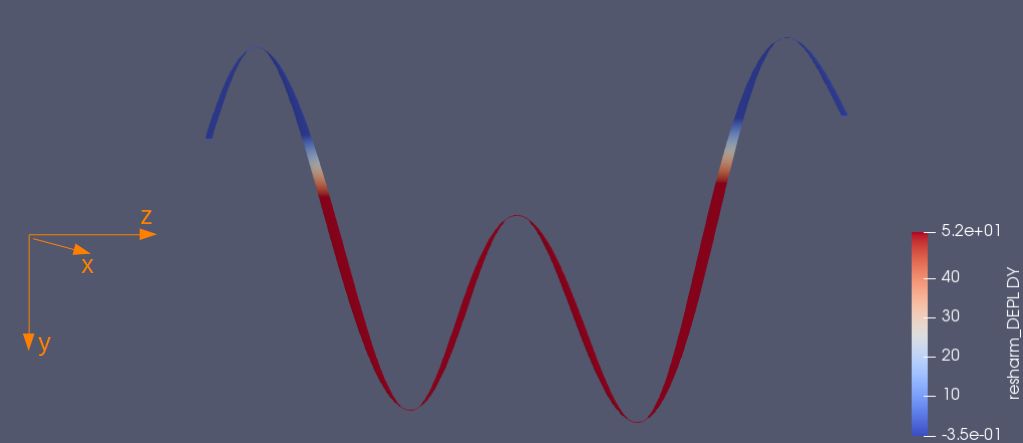
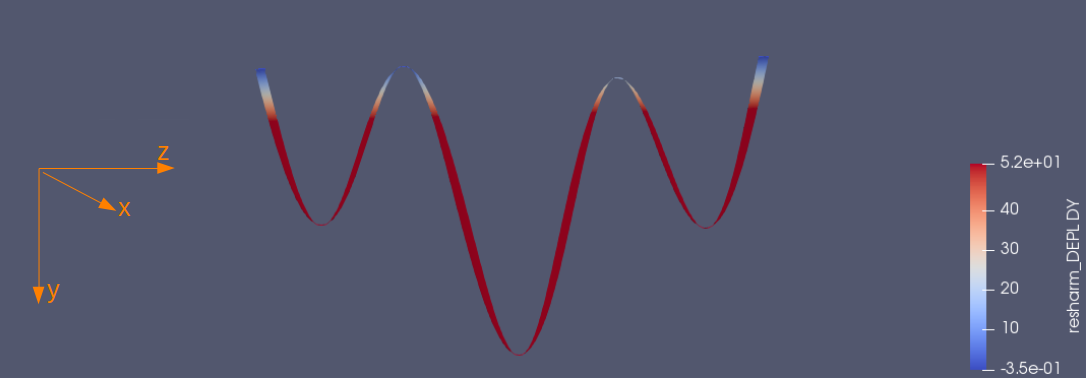
中心に1.16Hzと3.2Hzの振動を与えたときの比較 [#j7e3c02b] 振動を与えた点(中心部)のy方向変位
y方向の最大変位
1.16Hz:11070.7mm　　3.2Hz:4837.51mm
y方向の最小変位
1.16Hz:-10744.2mm　 3.2Hz:-4925.62mm

↑

両端から5mmの位置に振動を与える解析†

振動を与える位置のモデル

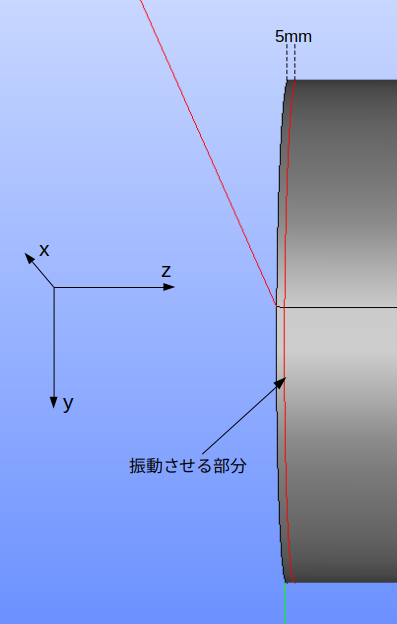
両端から5mmの位置に0.122Hzの振動を与える解析を行った。
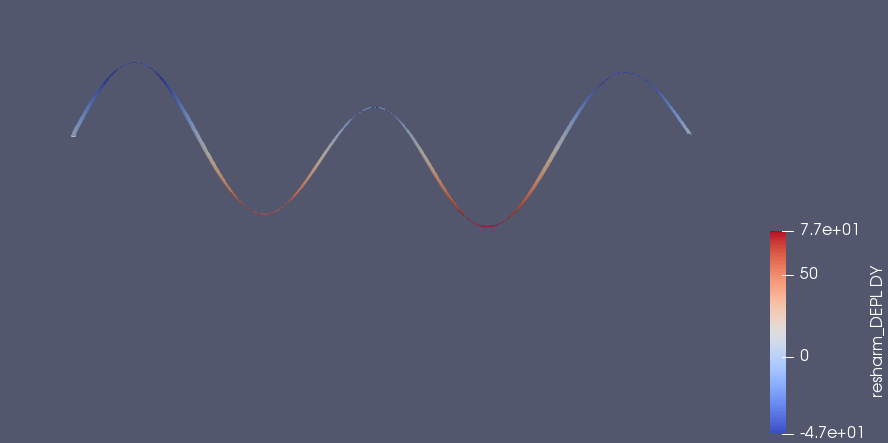
振動モードは下のように、１次モードとなった。

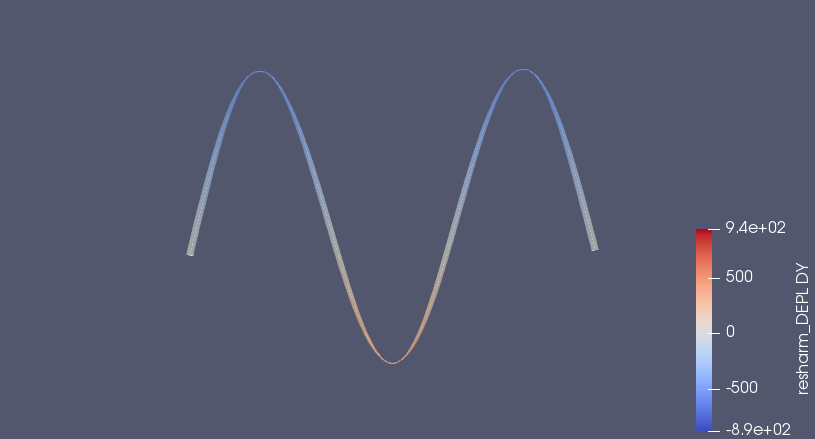
両端から5mmの位置に1.16Hzの振動を与える解析を行った。~[#bed94dc2] 振動モードは下のように、３次モードとなった。

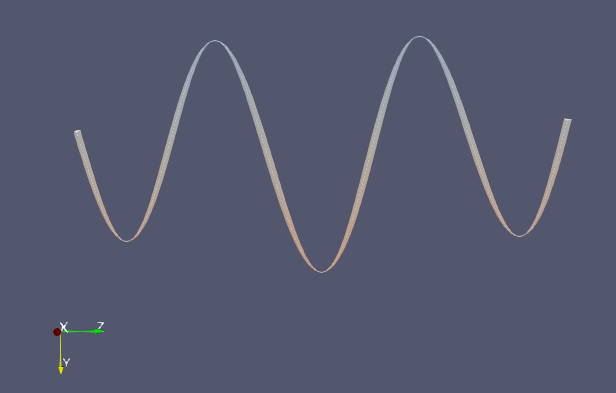
両端から5mmの位置に3.2Hzの振動を与える解析を行った。~[#t5a9716f] 振動モードは下のように、５次モードとなった。

↑

6/27 張力の与え方を内部張力に変えて解析†

張力の与え方は、今までの解析では面載荷(FORCE_FACE)で与えていたが、今回の解析では内部張力(FORCE_INTERNE)に変えて解析を回した。
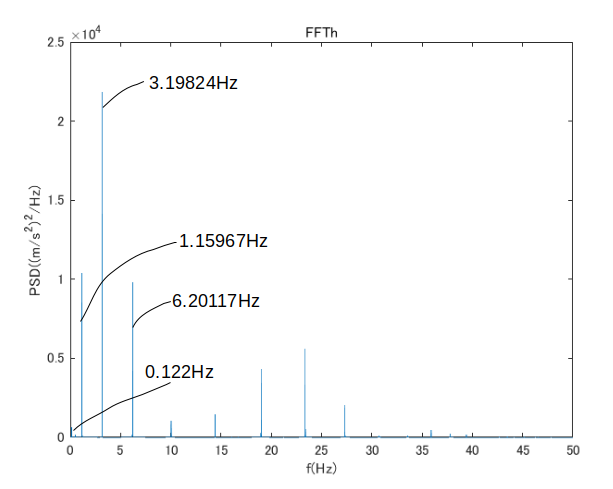
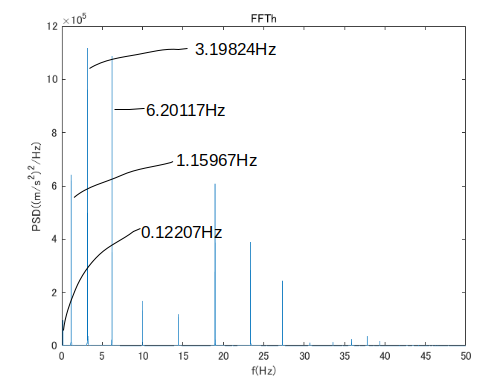
FFT処理をすると以下のような結果となった。(理論値は2.85Hz)

↑

6/28 ビーム要素(温度荷重ではない)†

ビーム要素で由利橋健全ケーブル(長さ71000mm、半径157.5mm)の解析を行ったところ、固有振動数は以下のようになった。(理論値は2.85Hz)
梁の曲げ振動数の理論値と等しくなった。

↑

由利橋　長さ71000mm、半径157.5mmの中央腐食モデル(長さ710mm,腐食半径157.5mm)†

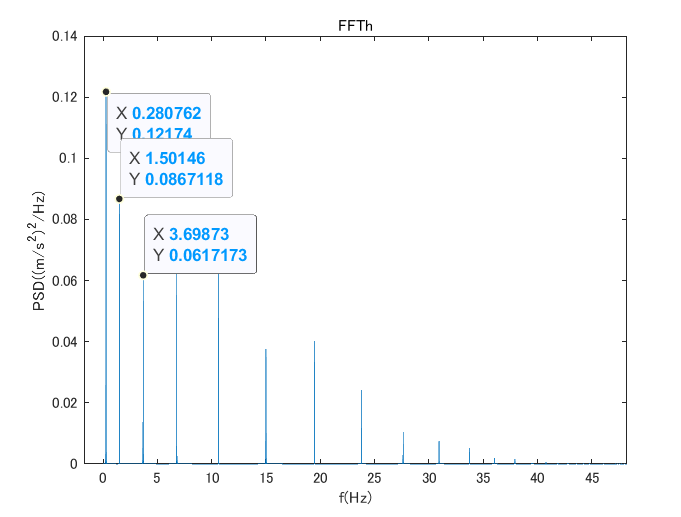
固有振動数の理論値 f=2.85Hz 　解析時間0〜100秒

載荷線と腐食部分

↑

やること†

クラックの解析
張力によって点がずれてしまっていることが考えられるため、中心に点を多く作って解析を行う。
正多角形で解析を行う。
要素数を多くする。
張力の与え方を温度荷重(ビーム要素、ソリッド要素)にする。
初期ひずみで張力の代わりを入れる
ローカルコーディネート

↑

進捗†

↑

7/11〜7/17†

7/12 引張試験の準備を行った。
7/15 今まで行ってきた解析結果を確認して、今後の解析で張力の与え方をどのようにしたらよいかを考えた。
・応力として線載荷で与えると張力がうまく入っていなかった。(0.122Hz、1.16Hz、3.20Hz)
・ビーム要素では梁の曲げ振動の値となった。(0.28Hz、1.50Hz、3.70Hz)
・強制変位(475mm)では25〜50Hzに多く卓越していた。また、張力が場所ごとにバラバラであった。
・内部張力(FORCE_INTERNE)では0.51Hz、1.16Hz、3.70Hzとなった。
・張力なしでは 7/16 引張試験を行った。使った鋼棒は腐食レベルが2-1のもの。
破断させることはできなかったが、応力-ひずみのグラフを作成すると第一降伏点(44.6kN)で勾配がゆるくなっていた。

↑

7/4〜7/10†

7/4 ネットで見つけた資料を参考にしながら温度荷重の解析を回した。
7/8 前回(4日)の温度荷重の解析を修正しながら再び解析を行った。
AnalysisにDYNA_VIBRAではなく、DYNA_NON_LINEを使うと解析がうまくいった。
7/9 今まで行っていた温度荷重の解析では100℃上昇させていたが、今日の解析では557.5℃上昇させた。
この557.5℃は、今まで行っていた張力(100MN)を与える解析でpoints71000での変位から計算した値。
7/10 強制変位させることで張力が入ることが分かったので、強制変位させて解析を行ってみた。

↑

6/26〜7/3†

6/26 今週はケーブル要素、ビーム要素、温度荷重の解析を行ってみる。
千代岡さんから温度荷重やビーム要素について教わった。また、ソリッド要素で内部張力を与える方法も教わった。
及川さんいただいた、ケーブル要素について解析を回してみたが「nddlリストにモデルがありません」というエラーが出た。
6/27 昨日、千代岡さんから教えていただいたソリッド要素に内部張力を与える解析とビーム要素について解析が回ったので結果を見た。
結果は上に書いているが、やはり理論値とは異なる値となった。
ケーブル要素のエラーについても調べていきたい。
7/1 青木さんがもらってきていただいたケーブルの引張試験の試し実験を行った。
いただいたケーブルはCASE1(健全)とCASE5(削孔+塩水注水)
7/2 ケーブル要素の解析がうまく回らなかった原因を考えたがわからなかった。
やはり、「nddlリストにモデルがありません」というエラーが出た。
7/3 今後は温度荷重と初期ひずみについて進めていく。

↑

6/20〜6/26†

6/20 由利橋のケーブルモデルの両端から5mmの位置に0.122Hzを与えて解析を行った。
結果は1次モードとなった。
6/21 中央部に張力がしっかりと入っているかを確認するため由利橋ケーブルモデルの中央部の主応力をみる解析を行った。
また、張力を2倍の200MNに変えた解析と左右で逆側に振動を与える解析も行った。
今日の解析では張力を2倍にしても振動数が√2倍になっていなかった。どこが良くなかったかを考えていきたい。
インパクトは今まで100kNを与えていたがモードを見るとあまり揺れていなかったため、1000kNに変更した解析もやってみた。
6/23 張力0の解析を行い、理論値と比較した。
結果は上に書いたが、張力を与えた場合よりも理論値が近くなった。
6/24 モデル中央部に張力分だけの応力が入っているかを調べた。しっかりと100MN分入っていた。
また、今まで線固定にして解析を行っていたが、張力を与える方の固定条件を面固定にして、張力が分解されないようにした。結果は明日見る。
明日は温度荷重について学びたいとおもう。

↑

6/13〜6/19†

6/13 振動(sin波)を与える解析を及川さんに教えていただいた。最初に1.16Hzのsin波を与えて解析を行った。与えたsin波がsin(2π1.16t)を入れたため揺れが小さかった。
そこで50000sin(2π1.16t)として50kNの振動を与えた。結果は明日確認する。
6/14 50kNの振動を両端に与えて解析を回したがうまく結果が見られなかった。
そこで振動を両端ではなく、中心の点に1.16Hzの振動を与えて解析をした。
結果は上の(由利橋健全モデルに1.16Hzの振動を与える解析)に書いているが、予想していたモードと異なっていた。
6/15 昨日の解析を3.2Hzにして解析を行った。
結果は上の(由利橋健全モデルに3.2Hzの振動を与える解析)に書いている。
1.16Hzの振動を与えた場合と3.2Hzの振動を与えた場合のy方向の最大変異と最小変異を比較した。
また、由利橋(長さ71000mm、半径157.5mm)の固有振動数の理論値である2.85Hzの振動を与えた解析も行った。
6/18 振動させる位置を両端から5mmの位置に変えて、1.16Hz,3.2Hz,2.85Hzの振動を与えた。
1.16Hzでは３次モード、3.2Hzでは５次モードとなった。

↑

5/30~6/12†

5/30 真杜くんの実験のサポート
5/31 実験サポート
6/3 100mm,半径0.5mmの解析の結果をまとめようとしたが、パソコンが重くなりまとめることができなかった。
6/4 パソコンが重く、結果が見れなかったため振動を検出する時間を15〜30秒とした。

時間	行うこと
0〜5秒	張力(1N)をかける。
5〜14.99秒	ケーブルを安定させる。
15秒	10Nの力を与える。
15.01〜30秒	卓越した振動を検出する。

6/5 上記の時間で解析したがパソコンがフリーズしてしまい結果が見れなかった。
6/6 山本さんの解析では長さ50m・半径75mmで行っており、今回の解析では長さ1000mm・半径0.5mmで行った。そこで張力を3.2MN→1N、中央部への線載荷を100KN→10Nとして解析を回した。
結果を得ることができた。明日、青木さんにFFT処理をお願いする。
6/7 長さ1000mm、半径0.5mmの中央部に100mm腐食を与えたモデルの解析を行ったがマトリクスエラーが出た。
長さ100mm、半径0.5mmの中央部に10mm腐食を与えたモデルでは解析が回った。
細長比によるエラーかもしれない。
長さ1000mm半径0.5mmモデルの細長比は3544.91
長さ100mm半径0.5mmモデルの細長比は354.5
6/8 由利橋のケーブル(長さ71000mm、半径157.5mm)の健全モデルの解析を回し、結果を青木さんに提出した。
月曜日に青木さんにFFT処理を依頼する。
6/9 由利橋のケーブル(長さ71000mm、半径157.5mm)の中央腐食モデル(長さ710mm、腐食半径157.5mm)の解析を回し、結果を青木さんに提出した。
月曜日に青木さんにFFT処理を依頼する。
6/10 FFT処理の行い方を学んだ。理論値とズレが生じたため、今後はなぜズレが生じたのかを調べるための解析も行っていきたい。
6/11 由利橋の健全モデルの解析値(3.2Hz)と理論値(2.85Hz)に差が生じた原因が張力の入れ方にあると思ったため、張力の入れ方を変えて解析した。
最初の解析では、面載荷に張力(100MN)を円の断面積で割った値を与えて解析した。そこを山本さんの昨年度の解析と同様に、張力(100MN)をMeshサイズでの面積で割った値を与えた。
どちらの解析の結果もf=3.2Hzとなっていたため、他の考えられる原因を探りたい。

↑

5/15〜5/29†

・山本さんの卒論の振動解析を解析してみる。
山本さんの解析では測点を３点設定していたが、モードをより詳細に調査するために９点設定して解析した。
5/16 山本さんの卒論，角田さんの修論を読んだ．
5/17 健全モデル、中央10m腐食、中央1m腐食のモデルを作った。
5/20 健全モデルのAster Studyを設定し，解析を回してもらう．
中央に線荷重を与える際は，3.2MNを断面積(半径75mmの円)で割った．(山本さんの卒論ではメッシュの切り方によって面積を変えていた．)
5/21 昨日設定したAster Studyのコードの意味を調べた．
5/23 健全モデルの解析を回した。

50m 半径75mm　健全モデル(点は下の写真の上部に設置した。)

50m 半径75mm　中央1m腐食

↑

MATLAB†

　1,変数→新規変数→処理したいデータを入れる
　2,FFTcable→データ名、スタート点(私の解析ではインパクトを与えた時間 ex)15s→1500)　卓越した振動数が出力される。
　3,bandcable→下限値・上限値、データ名、スタート点の入力
　4,C1P3→csvファイルで波形を描く

↑

振動(sin波)の与え方†

　1,csv形式でデータを作る。私の解析ではインパクトを与えた時からの所定の振動数のsin波のデータを作成する。
　2,Functions and Lists→DEFI_FONCTION→VALEにcsvファイルをインポート、NOM_PARAにINST
　3,BC and Load→AFFE_CHAR_MECA_F→FORCE_NODALE→振動させたい部分(点・線・面)と方向を選択する。
　4,Analysis→DYNA_VIBRA→EXCIT→CHARGEに3を選択

下の設定で解析をすると2重境界条件のエラーが発生した。
1

func1 = DEFI_FONCTION(
 NOM_PARA='INST', 
 VALE=(0.0, 0.0, 14.99, 0.0, 15.0, 29389.2626146241, 15.01, 26365.5875737644, 15.02, 23201.9148313981, 15.03, 19915.0430615916, 15.04, 16522.4251085748, 15.05, 13042.0753144948, 15.06, 9492.47386570505, 15.07, 5892.46866546789, ...)) # sequences have been limited to the first 20 occurrences.

func3 = DEFI_FONCTION(
 NOM_PARA='INST', 
 VALE=(0.0, 0.0, 100.0, 0.0))

load3 = AFFE_CHAR_MECA_F(
 DDL_IMPO=(_F(
     DX=func3, 
     DY=func1, 
     DZ=func3, 
     GROUP_MA=('kotei1', )
   ), _F(
     DX=func3, 
     DY=func1, 
     GROUP_MA=('kotei2', )
   )), 
 MODELE=model)

↑

SALOME エラー†

!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

  ! <S> Exception utilisateur levee mais pas interceptee.                          !
  ! Les bases sont fermees.                                                        !
  ! Type de l'exception : error                                                    !
  !                                                                                !
  !      Erreur écriture de l'enregistrement 766379 sur la base : VOLATILE 48      !
  !      code retour : -4                                                          !
  !      Erreur probablement provoquée par une taille trop faible du répertoire de !
  ! travail.                                                                       !
  !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

↑

実験†

↑

鋼棒の引張実験†

鋼棒の第一降伏点1160MPa 荷重=1160(N/mm2)☓(3.5☓3.5π)=44.6kN
・ジグへの鋼棒の設置方法
引張実験を行う際に曲げが入らないようにジグの中央に垂直に鋼棒を設置する。

・ひずみ装置の操作
最初にスタートを押し、測定開始時にもう一度スタートを押す。
その後は一定の間隔でスタートを押していく。

・結果の処理の仕方
1,ひずみの表
①ひずみゲージ1〜4の各結果に☓10^(-6)を行う。
②各ひずみゲージの最初の値を0にするために、得られた各値を補正する。

2,荷重と伸びの表
①0sと実験時にスタートボタンを押した間隔ごとに荷重を抽出する。
　ex)実験時に30sごとにスタートボタンを押した場合、0s、30s、60s、90s・・・時の荷重を抽出する。
②0s時の荷重を0にするように各値を補正する。
③補正した荷重を断面積で除して応力を求める。

3,応力-ひずみのグラフ作成
1で得たひずみの値と2で得た応力から、応力-ひずみのグラフを作成する。
ひずみゲージが4つあるときは、4本の線が1つのグラフに入るように作成する。

4,ヤング率の計算
・ひずみの表から計算する方法
①2で得た最大応力の10%と40%時の応力と各ひずみゲージのひずみの値を抽出する。
②E=(σ40%-σ10%)/(ε40%-ε10%)から計算する。
・伸びから計算する方法
①2で得た最大応力の10%と40%時の応力と伸びを抽出する。
②E=(f/A)☓(l/x)=(σ40%-σ10%)☓(l/(x40%-x10%)から計算する。(l：スパン　x：伸び)

↑

創造工房実習†

↑

2023 12月8日　創造工房実習†

サンドウィッチ梁

メッシュの長さ	要素数	変位(mm)	相対誤差(%)	計算者
0.7	155192	0.08378905246	15.365	安藤
0.8	138808	0.08380386491	15.350	安藤
0.9	82587	0.083707073981	15.45	兼田
1.1	38671	0.084201207602	14.95	兼田
1.2	31929	0.083688	15.466	柴田
1.3	28621	0.083669	15.4857	柴田
1.4	28854	0.08368	15.47	佐藤
1.5	20015	0.084052	15.10	佐藤
1.6	19448	0.0835402938	15.62	皆川
1.7	13801	0.0834355098	15.72	皆川
1.8	12528	0.083733	15.42	永山
1.9	11769	0.083924	15.23	永山
2	10699	0.084076876559	15.074	辻
3	3579	0.08414561753	15.004	辻
4	1628	0.082794	16.37	服部
5	1016	0.083033	18.89	服部
6	839	-0.082882	16.26	梶原
7	554	-0.080871	18.28	梶原
8	285	0.079995	19.20	工藤
9	261	0.078980	20.22	工藤
10	232	0.081911	17.26	佐々木
11	208	0.075676	23.56	佐々木

↑

2023 11月29日　創造工房実習†

異方性一次 [#p29b4460]

異方性一次

メッシュ長さ	要素数	変位	相対誤差	計算者
0.7	144563	0.505252	2.76	安藤
0.8	141517	0.504692	2.64	安藤
0.9	91648	0.502595	2.216	兼田
1.1	27160	0.489914	0.363	兼田
1.2	24675	0.487088	0.791	柴田
1.3	23446	0.4868010	0.995	柴田
1.4	17738	0.485999	1.16	佐藤
1.5	15438	0.485180	1.33	佐藤
1.6	15900	0.483286	1.71	皆川
1.7	12142	0.477952	2.80	皆川
1.8	11604	0.482085	1.9554	永山
1.9	10391	0.470887	4.2329	永山
2	10291	0.480910	2.19	辻
3	2328	0.431937	12.15	辻
4	1500	0.430156	12.52	服部
5	432	0.282968	42.45	服部
6	356	0.3441556	30.00	梶原
7	196	0.213934	56.49	梶原
8	104	0.229874	53.25	工藤
9	81	0.232308	52.75	工藤
10	78	0.203271	58.65	佐々木
11	63	0.222316	54.78	佐々木

等方性二次 [#vb0def3f]

等方性二次

メッシュ長さ	要素数	変位	相対誤差	計算者
0.7	144563	0.430124	3.22	安藤
0.8	141517	0.430132	3.22	安藤
0.9	91648	0.430020	3.197	兼田
1.1	27160	0.429828	3.151	兼田
1.2	24675	0.429836	3.15	柴田
1.3	23446	0.42974	3.13	柴田
1.4	17738	0.429797	1.3	佐藤
1.5	15438	0.429958	3.14	佐藤
1.6	15900	0.429755	3.18	皆川
1.7	12142	0.429676	3.11	皆川
1.8	11604	0.429829	3.1507	永山
1.9	10391	0.429684	3.1159	永山
2	10291	0.429620	3.10	辻
3	2328	0.429169	2.99	辻
4	1500	0.429254	3.01	服部
5	432	0.428170	2.75	服部
6	356	0.428452	2.82	梶原
7	196	0.42591	2.21	梶原
8	104	0.426074	2.25	工藤
9	81	0.425552	2.12	工藤
10	78	0.488382	17.20	佐々木
11	63	0.423972	9.0534	佐々木

↑

2023 11月24日　創造工房実習†

単純梁

メッシュの長さ	要素数	変位[mm]	相対誤差	計算者
0.7	145234	0.422484	1.388	安藤
0.8	142973	0.422570	1.409	安藤
0.9	91648	0.420437	0.897	兼田
1.1	27160	0.405618	2.659	兼田
1.2	24675	0.404349	2.96	柴田
1.3	23446	0.404185	3.00	柴田
1.4	17738	0.398604	4.34	佐藤
1.5	15438	0.396593	4.83	佐藤
1.6	16122	0.398212	4.44	皆川
1.7	12026	0.393411	5.59	皆川
1.8	11604	0.393668	5.53	永山
1.9	10391	0.390695	6.24	永山
2	10921	0.395103	5.18	辻
3	2328	0.324762	22.06	辻
4	1500	0.155013	62.80	服部
5	432	0.065278	84.33	服部
6	357	0.213062	48.87	梶原
7	196	0.1019	75.55	梶原
8	104	0.1158624	72.20	工藤
9	81	0.1255118	69.88	工藤
10	78	0.07733	81.44	佐々木
11	63	0.1999	52.03	佐々木

↑

2023 11月17日　創造工房実習†

Salomeの使い方を学んだ。
Geometry
Mesh作成
Aster Study
Pravis

片持梁

メッシュ長さ	要素数	先端変位(4隅の平均値)[mm]	相対誤差	計算者
0.7	198464	6.54281	1.91	安藤
0.8	113812	6.5104	2.39	安藤
0.9	40280	6.3631525	4.60	兼田
1.1	30055	6.3363525	5.00	兼田
1.2	26467	6.3043375	5.48	柴田
1.3	25180	6.304355	5.48	柴田
1.4	32212	6.31612	5.31	佐藤
1.5	17753	6.1209	8.23	佐藤
1.6	14296	6.2044625	6.98	皆川
1.7	13596	6.2156625	6.81	皆川
1.8	2866	5.737755	13.98	永山
1.9	6001	5.7263625	14.15	永山
2	5617	5.6458525	15.355	辻
3	2309	5.4728755	17.948	辻
4	617	3.6160575	45.12	服部
5	494	3.8580375	42.16	服部
6	581	2.50682	62.416	梶原
7	133	1.41225	78.82	梶原
8	78	1.2887175	80.68	工藤
9	72	1.2879925	80.69	工藤
10	60	1.14344	82.85	佐々木
11	65	1.23124	81.154	佐々木

↑

2023 11月10日　創造工房実習†

↑

2023 10月27日　創造工房実習†

　コマンドを学んだ。次回までに使いこなせるように頑張りたい。
pwd 今いる場所がわかる
ls ファイルを表示する
mkdir　ファイル名　　　ファイルの作成
rmdir　ファイル名　　　ファイルの削除
cd　ファイル名　　　ファイル名のところへ移動
vi　ファイル名　　　編集
esc : w　　保存
esc : q　　戻る
cp　コピー元　コピー先　　　コピーする時

皆川恭輔

皆川の卒論日誌 の履歴(No.37)

卒論†