柴田真杜の修論日誌の履歴(No.30)

やること
サグモデルの座標、軸力の計算方法
- さぐありモデルの作成
サグありモデルの作り方
サグの理論式
サグありモデルのt100のみを引っ張ったときのサグ
サグありモデルで各ノードに力を与えた場合
サグありモデルのt100のみを引っ張ったとき各ノードの張力
5月2日
- 実験モデル
- 解析
今後の課題
実橋と相似な実験モデルの作成
ナビエストークス方程式の無次元化
midasによるモデル化
midas静的解析の妥当性確認
由利橋モデルの作成
温度荷重について

やること†

midasで時刻歴解析を行うとき、釣合状態(初期軸力とおもりの荷重が釣り合った状態)を初期条件にもってくる方法を調べる
midasで風による力を何とかして再現できないか、ケーブルの後ろにできる渦は再現できなくてもいいから(実験のケーブル単体のモデル)
実験での風速を決める
ケーブルにあたる風の周期的なものを調べる。(sin波なのかなど)
風の周期をカルマン渦の周波数にしてもいいのか

↑

サグモデルの座標、軸力の計算方法†

高さ：h、径間長：ｌ、l/2におけるサグ：f、単位長さ重量：w はわかっているものとする。 L：ケーブル形状長、x1 y1：下端、xm ym：中央、x2 y2：上端

\( \sqrt{L^2 - h^2}= 2C \sinh\left( \frac{l}{2C} \right), \quad \frac{h}{L} = \tanh\left( \frac{x_m}{C} \right), \quad y = C \cosh\left( \frac{x}{C} \right), \quad f = \frac{h}{2} - (y_m - y_1), \quad x_m = \frac{x_2 + x_1}{2}, \quad l = x_2 - x_1 \)

これらの式から\( f - \frac{h}{2} + C \cosh\left( \frac{x_m}{C} \right) - C \cosh\left( \frac{x_1}{C} \right) = 0 \) これを解くとC(カテナリー数)が求まる。

ここで\( x_m = C\, \mathrm{arctanh}\left(\frac{h}{L}\right), \quad x_1 = x_m - \frac{l}{2} \)

Cを求めるここができたら下端、上端のx,y座標を求める。x座標を一定の間隔で分割する。x座標に対応するy座標を求める。
軸力は \( T = w y \)で各要素ごとを求める。

↑

さぐありモデルの作成†

cable要素を使用したサグありモデルを作成した。

↑

サグありモデルの作り方†

[1]まずサグのないまっすぐなcable要素を用意する
cable要素のみの場合、解析がエラーになってしまうため、固定部に壁を想定したマルチファイバー要素を結合した
[2]cableに張力、重力を与えたときの100点の座標を読み取る
このときサグは2.2m
[3]読み取った座標をプロットし(各点をt0〜t100とする)100点を線で結ぶことでサグありモデルを作成した。

↑

サグの理論式†

ケーブル長さl(重力がかかっていないまっすぐな状態)、サグfを利用して張力、反力を求めることができるみたいだが、この逆をすることで張力からサグを求める
まずt100の張力(水平力)をH、単位長さ重量をwをしたとき、\( \gamma =w/H \)を求める
\( \sinh((\gamma*l)/4)=\sqrt((\gamma*f)/2) \)よりサグfを求める
この式からサグの理論値は2.2mとなった

↑

サグありモデルのt100のみを引っ張ったときのサグ†

t100を1003.69kNの力で引っ張ったときのサグは2.1m 理論値と近い値になった。

↑

サグありモデルで各ノードに力を与えた場合†

解析がまわらない。

↑

サグありモデルのt100のみを引っ張ったとき各ノードの張力†

各ノードの張力をプロットした

↑

5月2日†

↑

実験モデル†

ケーブルにおもりをつけることでサグを再現し、揺らしたときの挙動再現を解析で行おうとした。
しかしおもりがいろんな方向へ揺れてしまい再現は難しそう。もう一度実験方法を考える必要あり。

塔の高さ:900mm
ケーブルの長さ:845mm（正確ではない可能性あり)
鉛の間隔と1つ1つの重さ:1つ目の重りがケーブルと塔のつなぎ目から30mm、2つ目の重りから25mmで分布し、重りは全部で30個。
　　　　　　　　　　　重さは0.9g、0.9g、2.1gの順になっている。
最初のサグの大きさ:鉛直方向に25mmだがこれも左右で多少の差があり、正確ではない可能性あり。

↑

解析†

おもりを荷重として各ノードに下方向の力を与える方法と、おもりの質量をノードに与える方法の2つを試した。
・荷重として与える方法
おもりの重さを力として与えた場合、奥方向には変位しなかった。

・質量として与える方法
質量を加え横に押すまでの挙動は荷重でサグを再現したときと近くなった。
しかし、横向きの力をなくしたあとの挙動が荷重による方法と違いが生じた。

↑

今後の課題†

由利橋のケーブルが揺れた原因をさぐる。
実橋と相似な実験モデルを作成し由利橋のケーブルの揺れを実験で再現する。さらに解析でも再現する。
由利橋モデルの作成
由利橋モデルに温度を与えた時(静的解析)の挙動を見る。仮定では主塔がS字になる。

↑

実橋と相似な実験モデルの作成†

物理現象の支配方程式を無次元化させ、無次元パラメータを求める。
無次元パラメータを一致させてスケールダウンさせた実験モデルを作る。
非線形ケーブル運動の支配方程式

\[\frac{\partial}{\partial x} \left[\left( \sigma^{(s)} + \sigma \right) \frac{\partial u}{\partial x} + \sigma　\right ] + X = \rho \frac{\partial^2 u}{\partial t^2}\]

\[\frac{\partial}{\partial x} \left[ \left( \sigma^{(s)} + \sigma \right) \frac{\partial v}{\partial x} \right ] + Y = \rho \frac{\partial^2 v}{\partial t^2}\]

\[\frac{\partial}{\partial x} \left[ \left( \sigma^{(s)} + \sigma \right) \frac{\partial w}{\partial x} + \sigma \frac{d}{dx}w^{(s)} \right] + Z = \rho \frac{\partial^2 w}{\partial t^2}\]

\( \sigma \)(s):静的応力、\( \sigma \):動的応力、w(s):さぐ、w:動的鉛直変位 X,Y,Z:x,y,z方向外力

軸方向の力が最もケーブルの運動に影響を及ぼすと考えられるため、xにおける方程式を無次元化させた。

\( x = L x^*, \quad u = L u^*, \quad \sigma = a \sigma^*, \quad t = b t^*, \quad X = \rho g X^* \)とし,

\[\frac{\partial}{\partial x} \left[\left( \sigma^{(s)} + \sigma \right) \frac{\partial u}{\partial x} + \sigma　\right ] + X = \rho \frac{\partial^2 u}{\partial t^2}\]

を変形する

\[\frac{1}{L} \frac{\partial}{\partial x^*} \left[ \left( a \sigma^{(s)*} + a \sigma^* \right) \frac{\partial u^*}{\partial x^*} + \sigma^* \right] + \rho g X^* = \rho \frac{L}{b^2} \frac{\partial^2 u^*}{\partial t^{*2}}\]

\[\longrightarrow\]

\[\frac{a b^2}{\rho L^2} \frac{\partial}{\partial x^*} \left[ \left( \sigma^{(s)*} + \sigma^* \right) \frac{\partial u^*}{\partial x^*} + \sigma^* \right] + \frac{b^2 g}{L} X^* = \frac{\partial^2 u^*}{\partial t^{*2}}\]

\( b = \sqrt{\frac{L}{g}} \)と決定する。

\( \sigma = E \varepsilon \)より上式は次のようになる。

\[\frac{a E}{\rho g L} \frac{\partial}{\partial x^*} \left[ \left( \varepsilon^{(s)*} + \varepsilon^* \right) \frac{\partial u^*}{\partial x^*} + \varepsilon^* \right] + X^* = \frac{\partial^2 u^*}{\partial t^{*2}}\]

\( \varepsilon \)は無次元量のため方程式は無次元化され、係数\( \frac{a E}{\rho g L} \)を実橋と実験で一致させることで相似な実験が可能となる。

↑

ナビエストークス方程式の無次元化†

ナビエストークス方程式

\[\rho \left(\frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u}\cdot\nabla)\mathbf{u} \right) = -\nabla p + \mu \nabla^{2}\mathbf{u} + \mathbf{f} \]

レイノルズ数の導出
レイノルズ数：流体中の慣性力（流体の運動量）と粘性力（流れを抑制しようとする力）の比を表す無次元量

\[ \boldsymbol{u} = U\, \boldsymbol{u}^*, \quad t = (L/U) \, t^*, \quad \nabla = \frac{1}{L}\, \nabla^*, \quad p = \rho U^2\, p^* \]とし、\[ L / \left(\rho U^2\right) \]をかけると

\[\frac{\partial \boldsymbol{u}^*}{\partial t^*} + \left( \boldsymbol{u}^* \cdot \nabla^* \right)\boldsymbol{u}^* = -\nabla^* p^* + \left( \frac{\rho U L}{\mu} \right)\nabla^{*2}\boldsymbol{u}^* + \left( \frac{\rho U^2}{L} \right)\boldsymbol{f} \]

\[f = (\rho\, U^2) / L \, f^*\]　とする

\[ \frac{\partial \boldsymbol{u}^*}{\partial t^*} + \left( \boldsymbol{u}^* \cdot \nabla^* \right) \boldsymbol{u}^* = - \nabla^* p^* + \frac{1}{\mathrm{Re}} \nabla^{*2} \boldsymbol{u}^* + \boldsymbol{F}^* \]

ここでRe（レイノルズ数) = (\( \rho U L ) / \mu \)
ナビエストークス方程式の無次元化でレイノルズ数が導出される。

ストローハル数の導出
ストローハル数：ストローハル数は、流体中の物体に周期的な渦が放出される現象を記述する無次元数。この数は、流れの周波数、物体の代表的な寸法、流体の速度という3つの物理量から構成される。
代表時間スケールT=1/fv fv:カルマン渦の周波数

\[ \frac{\partial \boldsymbol{u}^*}{\partial t} = \frac{\partial (U \boldsymbol{u}^*)}{\partial (T t^*)} = \frac{U}{T} \frac{\partial \boldsymbol{u}^*}{\partial t^*} \]

ナビエストークス方程式をこれらを使用し整理すると、

\[ \left( \frac{U T}{L} \right) \frac{\partial \boldsymbol{u}^*}{\partial t^*} + \left( \boldsymbol{u}^* \cdot \nabla^* \right) \boldsymbol{u}^* = - \nabla^* p^* + \left( \frac{\rho U L}{\mu} \right) \nabla^{*2} \boldsymbol{u}^* + \boldsymbol{f}^* \]

ここで \( St (ストローハル数) = L / (U T) = (fv L) / U \)

実物と模型の比較

動粘性係数は同じ。
模型の長さは実物の\( 1/59.58 \)としたので、\( L_{\text{実物}} = 59.58 L_{\text{模型}} \)
よって風速は次のように求まる。\( U_{\text{模型}} = 59.58 U_{\text{実物}} \)
実物の風速を由利橋のケーブルが大きく揺れた日の風速とすると、\( U_{\text{実物}}≒20m/s \)
したがって\( U_{\text{模型}}=1191.6m/s \)
これは不可能である。多くの風洞実験はレイノルズ数の一致をあきらめ、ストローハル数が比較的安定しているレイノルズ数領域（亜臨界領域）で実験を行う。
亜臨界領域のレイノルズ数は　\( 260 < Re < 2.8 * 10^5 \)　程度
由利橋のケーブルに作用する風のレイノルズ数を計算すると、\( 1.35*10^5 \)
例として、\( Re = 1*10^4 \) のとき　\( U_{\text{模型}}=88.3m/s \) 、 \( Re = 1*10^3 \)　のとき　\( U_{\text{模型}}=8.8m/s \)　となる。

渦励振はカルマン渦の放出周波数と物体の固有振動数が一致し、共振することでおきる。
カルマン渦は \( 40 < Re < 1000 \) で発生するといった資料があった。

↑

midasによるモデル化†

解析エラーが出てしまう．
エラーの内容はケーブルの各節点の自由度によるものである．
ケーブルの各節点を完全固定にすると解析は回るが，実験のようにX方向変位やｙ軸まわりの回転を許すとエラーになる．
幾何学的非線形を考慮することで自由度のエラーが消えた．
重りを節点荷重，張力を平衡要素の節点力という設定で解析を行った時の様子

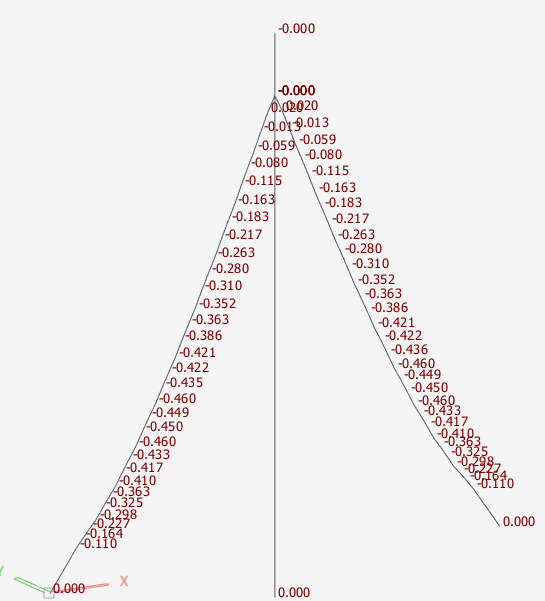
節点荷重とその際に生じる張力を導入することで，ケーブルの変位が0に近い値となった．

時刻歴解析 midasで時刻歴解析の方法を勉強中
現状
初期条件を設定することができていない。(静的解析の結果を本来は引き継げるが、今回の実験モデルは「非線形解析オプション」を入れないと静的解析が回らず、時刻歴解析では「非線形解析オプション」を使えないため)（「非線形解析オプション」を必要としないモデルの場合、引き継げるはず）
時刻歴解析では軸力を入れることができない?　節点力は入れれる。
そこで初期軸力を「幾何剛性用の初期軸力」、自重を時刻歴(1～10s)、主塔先端に節点力(10～30s)とすることで時刻歴解析を試みた。
このやり方では釣合状態の初期軸力を「幾何剛性用の初期軸力」で設定しているため、自重によってさらに軸力が導入される。
そこで釣合状態の初期軸力(「幾何剛性用の初期軸力」)をT、自重が入ったあとの軸力をT^*とし、「幾何剛性用の初期軸力」に\( {T - (T^* - T)} \)を入れることで、自重が入った後の軸力を釣合状態の軸力とした。
しかし、変位が釣り合わず、z方向に最大7mm変位してしまっている。
つまり、軸力は入れたいものが入ったが、元の状態から変位が生じ、釣り合っていない。

↑

midas静的解析の妥当性確認†

つり合い状態から強制変位させたときの変位後の座標と軸力を計算と解析で比較した．
計算と解析の結果を比較する時には基準とする点(今回は支点)を平行移動する必要がある．
x1、y1：手計算の支点、x2、y2：解析の支点としたとき
計算のx座標を解析のx座標にそろえるので、\( y = C \cosh\left( \frac{x - (x_2 - x_1)}{C} \right) + (y_2 - y_1) \)に解析のx座標を代入する．

○形状長0.88m、強制変位10mmのとき
　

○形状長0.88m、強制変位20mmのとき
　

○形状長0.9m、強制変位20mmのとき
　

強制変位させてもケーブルが伸びない範囲では座標と軸力が計算と解析でほぼ一致したことから，midasの静的解析の妥当性を確認.

↑

由利橋モデルの作成†

まずはケーブルをモデル化する。
いただいた図面を基に、
ケーブル固定間距離:ケーブルウェッジ間長、径間長:ケーブルウェッジ間長*cos(π/180*ケーブル角度)、高さ:ケーブルウェッジ間長*sin(π/180*ケーブル角度)、形状長:ウェッジ間曲線長　としてカテナリー数を計算、そこからケーブル形状、軸力を計算した。
軸力の実測値と、計算で求めた各節点力の平均が相対誤差が±0.5%になるよう形状長、ケーブル固定間長を変化させた。(図面には少数第３位までだったため第４位を四捨五入して図面の値になるように)

主塔とケーブルのみのモデル化ができた.
ケーブル形状を計算するとC1，C12のようについになっているケーブル同士のz座標が一致しなかったため，図面の主塔先端からの距離を揃えるよう平行移動した．

施工段階解析を使用し主塔にも内力を導入することで，ケーブル張力を導入時も主塔がまっすぐになった．

↑

温度荷重について†

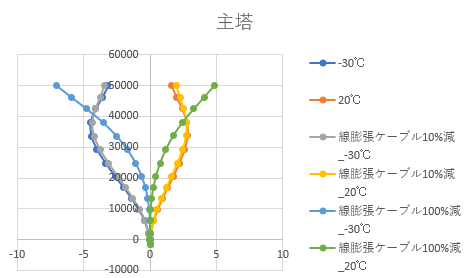
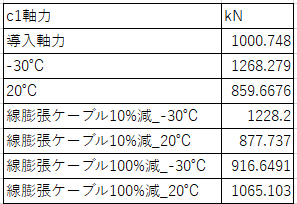
夏、冬の気温が重要になると考え、温度荷重を与えた．
温度を与える際に、ケーブルは被覆があるため、主塔に比べ線膨張係数が小さくなると考えられる．そこでケーブルの線膨張係数を10%落とした時、100%落とした時で主塔の動き、ケーブル張力を比較した．
　

30℃の場合、ケーブルの線膨張係数が10%の時では張力が大きくなり主塔が傾く．
ケーブル線膨張係数が０の結果から冬季にc1側に傾くが、それによりケーブル張力がゆるむよりも、ケーブルの伸縮による軸力増加の方が大きい．

柴田真杜の修論日誌 の履歴(No.30)