卒論日誌†
5月18日〜 初期不整を導入した90×90×1200mmの片側固定端†
- 90×90×1200mmの梁で片方を固定端にして、もう片方の自由端からZ方向に荷重をかけたときの縮みを求める。
- 比較するグラフは青木さんに貰った資料 "Composite timber-steel encased columns subjected to concentric loading" の中にあるグラフ
5月18日 ①初期不整なしの場合†
- 条件は、E=7500N/mm^2 ν=0.4 (木材)
- メッシュは5で切って、要素数は244700
- p17のP12-bare-CA(b)と比較をしたときのグラフは↓
- (bare=木材の中に何も入れていない状態、CA=接着剤が2つの木材ケーシング?界面の間にのみ塗布されているという意味)
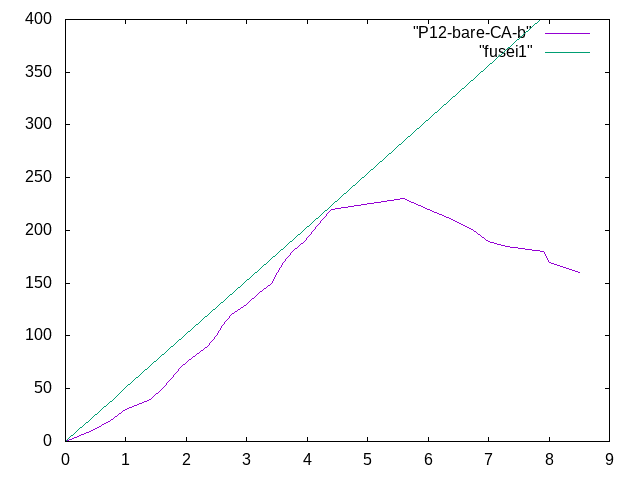
- 400kNまで荷重をかけたときの曲がり具合
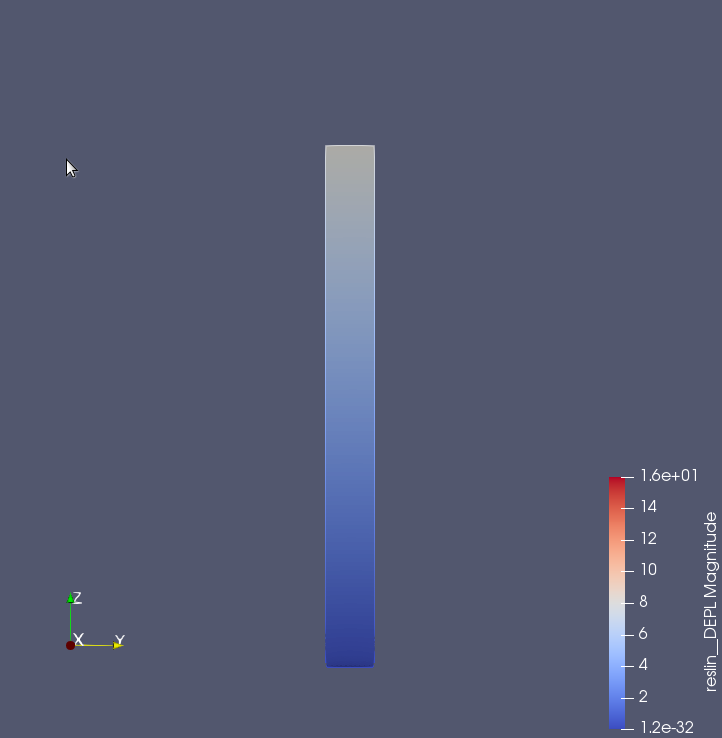
5月17日 今後の課題†
- 座屈解析は田村さんが行うので、私は初期不整を導入する方法で曲げる。
- ①初期不整なし
- ②上面と下面の面積を変えた場合
- ③上面の位置をずらした場合
- ④節を入れた場合
- 以上について400kNあたりまで荷重をかけて、400kNかけた時点での曲がり具合と、荷重-変位のグラフを求める。
5月13日 90×90×1200mmの片側固定端(囲みあり)†
- 90×90×1200mmの梁で片方を固定端にして、もう片方の自由端からZ方向に荷重をかけたときの縮みを求める。
- 88×88×1200mmの梁(木材)の周りを厚さ1mm鋼材で囲んだ梁を用いる。
- 条件は、P=-300kN 、E=206000N/mm^2 ν=0.3(鋼材)、E=7500N/mm^2 ν=0.4(木材)
- メッシュは5で切って、要素数は379073
- 縮み量は載荷面の平均を求めて、Z方向に -2.7507mm
- 理論値は(\( δ=\frac{PL}{EA} \))より、-2.7394mm
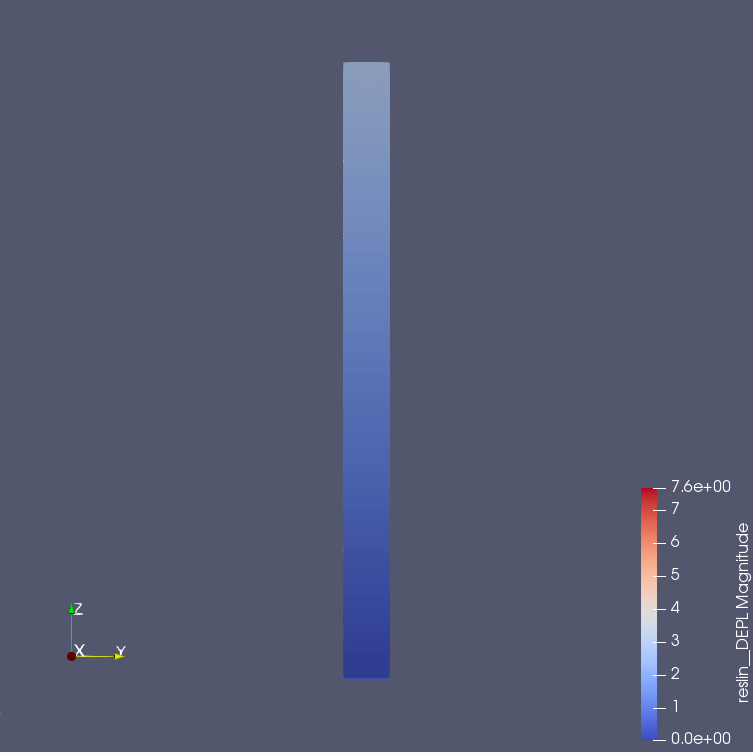
5月12日 90×90×1200mmの片側固定端(囲みなし)†
- 90×90×1200mmの梁で片方を固定端にして、もう片方の自由端からZ方向に荷重をかけたときの縮みを求める。
- 条件は、E=7500N/mm^2 ν=0.4 P=300kNと200kN (木材)
- メッシュは5で切って、要素数は244700
- P=300kNのとき、縮み量は載荷面の平均を求めてZ方向に -5.8992mm
- 理論値は(\( δ=\frac{PL}{EA} \))より、-5.9259mm
- 田村さんの解析の90×90×1200mmの梁の真ん中に16×16×1200mmの穴を開けた梁の縮みは -6.319215mmであったので、近い値にはなった。

- 次に、実験結果と比較をするためにP=200kNでの解析を行った。
- P=200kNのとき、縮み量は載荷面の平均を求めてZ方向に -3.9328mm
- 理論値は(\( δ=\frac{PL}{EA} \))より、-3.9506mm
- 実験結果のグラフはP=200kNのとき大体4mmほどの縮みだったので、実験結果と近い値になった。
5月10日 今後の課題†
- 次は、90×90×1200mmの梁で、片方を自由端、片方を固定端にして、自由端側からZ方向に荷重をかけた場合の縮みを求める。
- 材料は木材を想定。田村さんの解析と近い値になったら、周りを1mmの鋼材で囲んだ形でもう一度解析を行う。
- 終わったら座屈解析をやってみる(難しい…)
5月9日 200×200×2600mmの単純梁(囲みあり2材料)†
- 196×196×2600mmの梁(木材)の周りを厚さ2mm鋼材で囲んだ単純梁中央のたわみを求める。
- 条件は、P=1000kN 、E=206000N/mm^2 ν=0.3(鋼材)、E=7500N/mm^2 ν=0.4(木材)
- 中央(載荷線)のたわみの平均は122.23953mm
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は119.87165mm
- メッシュは15で切って、要素数は341186
5月9日 200×200×2600mmの単純梁(囲みあり1材料)†
- 前回(4月28日)囲いの厚さを0.2mmに間違えてしまった。今回はちゃんと2mmでやります。
- E=206000N/mm^2 ν=0.3 P=1000kN (鋼材)のとき
- 中央(載荷線)のたわみの平均は13.37029mm
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は13.3313mm
- メッシュは15で切って、要素数は341186
- E=7500N/mm^2 ν=0.4 P=1000kN (木材)のとき
- 中央(載荷線)のたわみの平均は365.79073mm
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は366.1667mm
- メッシュは15で切って、要素数は341186
4月28日 200×200×2600mmの単純梁(囲みあり1材料)(間違えた)†
- 穴を開けない方法で囲みありの単純梁中央のたわみを求める。
- 囲みありのときの方が要素数が少しだけ多くなった。
- 199.6×199.6×2600mmの梁の周りを0.2mmの厚さで囲んだ形の単純梁にする。↓こんな感じ。
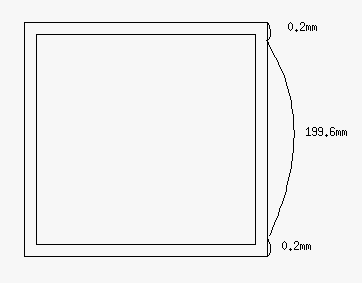
- E=206000N/mm^2 ν=0.3 P=1000kN (鋼材)のとき
- 中央(載荷線)のたわみの平均は13.43085mm
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は13.3313mm
- メッシュは10で切って、要素数は458588
- E=7500N/mm^2 ν=0.4 P=1000kN (木材)のとき
- 中央(載荷線)のたわみの平均は367.8057mm
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は366.1667mm
- メッシュは10で切って、要素数は458588
- 間違えて0.2mmでやってしまった(TT)時間がないので今度やります(TT)
4月28日 200×200×2600mmの単純梁(囲みなし) 昨日の訂正!!†
- 昨日の理論値は間違ってた!正しくは200×200×2600mmの単純梁だった!
- E=206000N/mm^2 ν=0.3 P=1000kN (鋼材)のとき
- 中央(載荷線)のたわみの平均は13.4314mm
- メッシュは10で切って、要素数は458140
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は13.3313mm
- E=7500N/mm^2 ν=0.4 P=1000kN (木材)のとき
- 中央(載荷線)のたわみの平均は367.822mm
- メッシュは10で切って、要素数は458140
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は366.1667mm
- 理論値に近い値になった〜!
4月27日 200×200×3000mmの単純梁(囲みなし)†
- とりあえず、穴を開けない方法で鉄の単純梁中央のたわみを求めた。
- E=206000N/mm^2 ν=0.3 P=1000kN のとき
- 中央(載荷線)のたわみの平均は13.4314mmとなった。
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は20.4794mmとなった。
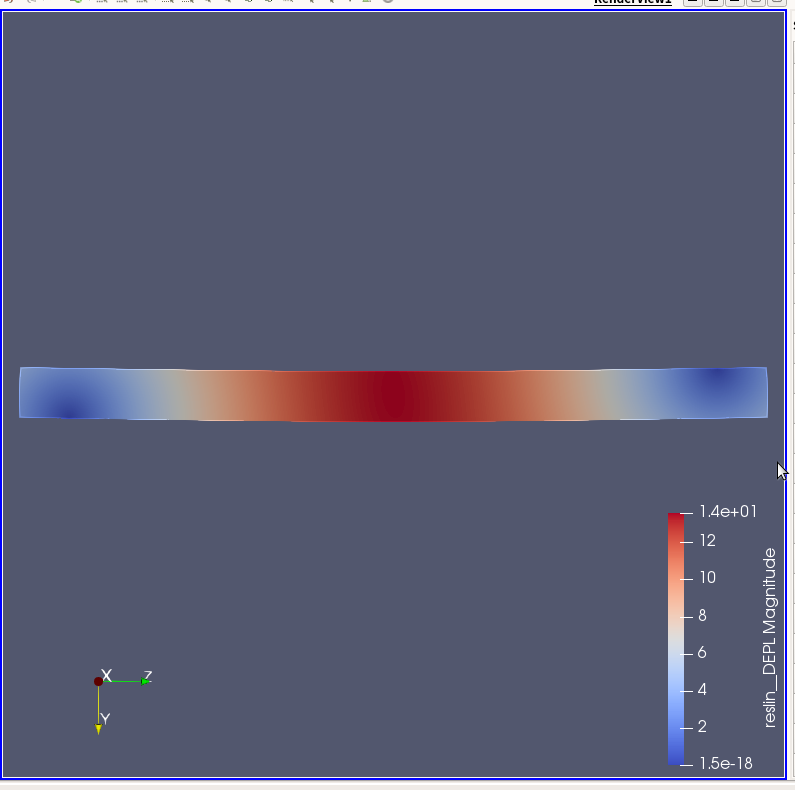
- 次に、木材の単純梁中央のたわみを求めた。
- E=7500N/mm^2 ν=0.4 P=1000kN のとき
- 中央(載荷線)のたわみの平均は367.822mmとなった。
- このとき、ティモシェンコ(\( v=\frac{P\ell^{3}}{48EI} \))により求めた理論値は562.5mmとなった。
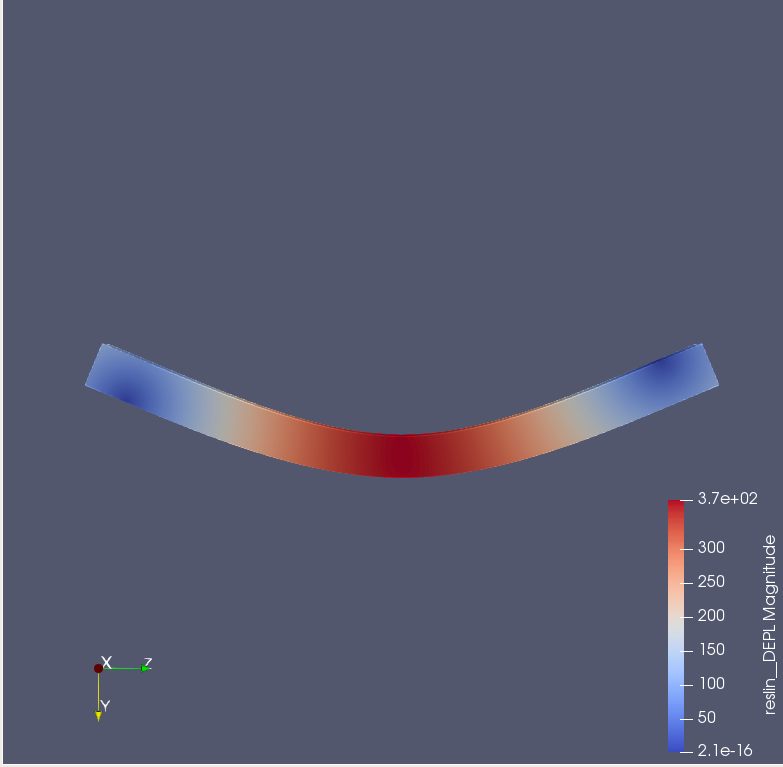
- 次は囲み(2mmくらい)ありの状態で計算を行いたいと思う。
4月21日 200×200×3000mmの単純梁(囲みなし)†
- Geometryで200×200×3000mmの単純梁モデルを作成した。
- ノートパソコンではなくなったのでCutを用いる方法で作ってみた。
- なぜか分からないがMeshの切り方がうまくいかず、どれだけ待っても進まなかった。
- メッシュの計算をキャンセルを押したところ、要素数が多すぎるみたいな表示が出てきた。
- メッシュの最大サイズを3000にしたときにメッシュを計算することは不可能と出てきた。なぜ(TT)
- →カットした穴の大きさの問題なのでは?と及川さんに助言してもらった。次はカットの穴を200×0.1×0.2mmではなく、200×1×2mmくらいでやってみたいと思う。
\( v=\frac{P\ell^{3}}{48EI} \)
作業日誌†
| 日付 | 時間 | 作業時間 | 内容 | 立会 |
| 10/16 | 14:30-16:00 | 1.5h | 顔合わせ、ノートPCの使い方 | 後藤先生、M2、4年生 |
| 10/23 | 14:30-16:00 | 1.5h | UNIXコマンドの使い方 | 後藤さん |
| 10/30 | 14:30-16:00 | 1.5h | viの使い方 | 後藤さん |
| 11/6 | 14:30-16:30 | 2h | Salome-mecaの使い方、片持ち梁 | 後藤さん、及川さん、4年生 |
| 11/13 | 14:30-16:30 | 2h | Salome-meca、単純梁 | 後藤さん、及川さん、4年生 |
11月6日課題†
| メッシュサイズ | 要素数 | 先端変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 394121 | 6.57938 | -1.4 | 君島 |
| 0.7 | 130916 | 6.4781 | -2.8 | 君島 |
| 0.8 | 72101 | 6.43695 | -3.5 | 高橋 |
| 0.9 | 71718 | 6.43136 | -3.6 | 高橋 |
| 1.0 | 72278 | 6.44302 | -3.4 | |
| 1.2 | 65575 | 6.408255 | -3.9 | 田村 |
| 1.4 | 41096 | 6.316155 | -5.2 | 田村 |
| 1.5 | 23417 | 6.120905 | -8.2 | 根本 |
| 1.8 | 11758 | 5.7368975 | -13.9 | 根本 |
| 2 | 11817 | 5.7382525 | -13.9 | 藤原 |
| 4 | 2862 | 4.9428 | -25.9 | 藤原 |
| 8 | 897 | 4.0411725 | -39.4 | 森島 |
| 10 | 596 | 3.4634575 | -48.1 | 森島 |
ヤング率:6000(N/mm^2) ポアソン比:0.4 理論値:6.67(mm)
11月13日課題†
| メッシュサイズ | 要素数 | 先端変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 391031 | 0.34118 | 2.35 | 君島 |
| 0.7 | 215780 | 0.33798 | 1.39 | 君島 |
| 0.8 | 159468 | 0.33563 | 0.69 | 高橋 |
| 0.9 | 90071 | 0.33203 | -0.39 | 高橋 |
| 1.0 | 61315 | 0.32997 | -1.2 | |
| 1.2 | 58111 | 0.329956 | -1.2 | 田村 |
| 1.4 | 47409 | 0.328156 | -1.5 | 田村 |
| 1.5 | 42068 | 0.325074 | -2.4 | 根本 |
| 1.8 | 24627 | 0.317161 | -4.8 | 根本 |
| 2 | 12228 | 0.3005115 | -6.9 | 藤原 |
| 4 | 5077 | 0.28405475 | -13.9 | 藤原 |
| 8 | 1795 | 0.23120033 | -30.6 | 森島 |
| 10 | 752 | 0.1612725 | -51.6 | 森島 |
ヤング率:7500(N/mm^2) ポアソン比:0.4 理論値:0.33334(mm)
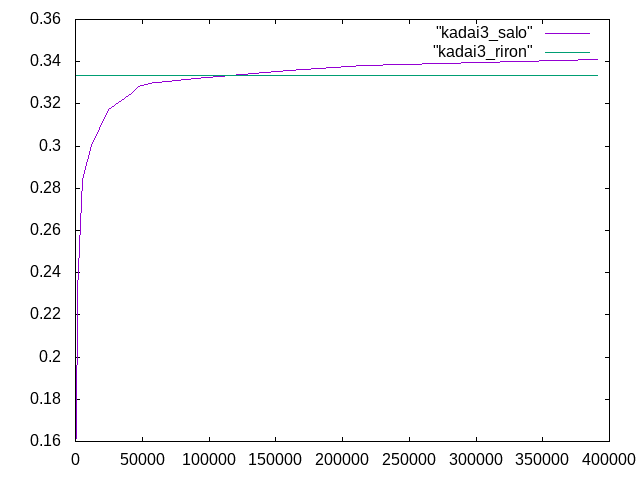
11月20日課題†
スパン100mm†
| メッシュサイズ | 要素数 | 先端変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 391031 | 0.440015 | 11.9 | 君島 |
| 0.7 | 215780 | 0.435823 | 10.8 | 君島 |
| 0.8 | 159468 | 0.4330131 | 10.1 | 高橋 |
| 0.9 | 90071 | 0.42766 | 8.72 | 高橋 |
| 1.0 | 61315 | 0.423881 | 7.77 | |
| 1.2 | 58111 | 0.423005 | 7.54 | 田村 |
| 1.4 | 47409 | 0.420309 | 6.86 | 田村 |
| 1.5 | 42068 | 0.418410 | 6.39 | 根本 |
| 1.8 | 24627 | 0.410464 | 4.36 | 根本 |
| 2 | 12228 | 0.396314 | 0.84 | 藤原 |
| 4 | 5077 | 0.378695 | -3.6 | 藤原 |
| 8 | 1795 | 0.342299 | -12.7 | 森島 |
| 10 | 752 | 0.298709 | -24.0 | 森島 |
ヤング率:7500(N/mm^2) ポアソン比:0.4 理論値:0.393334(mm)
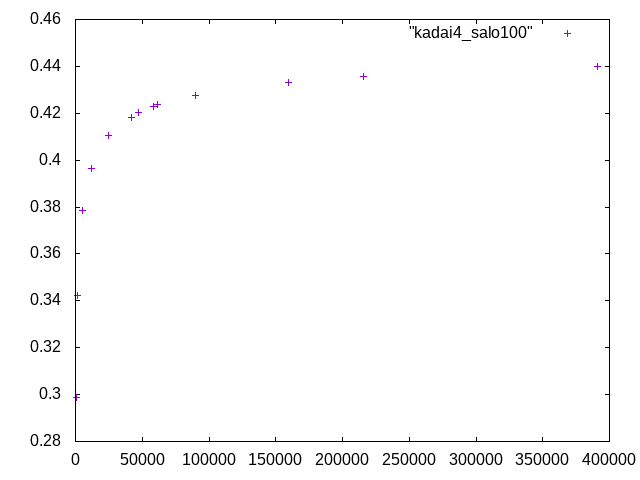
スパン50mm†
| メッシュサイズ | 要素数 | 先端変位(mm) | 相対誤差(%) | 計算者 |
| 0.5 | 251781 | 0.1253048 | 74.8 | 君島 |
| 0.7 | 109175 | 0.1172535 | 63.6 | 君島 |
| 0.8 | 75902 | 0.11527 | 60.8 | 高橋 |
| 0.9 | 71911 | 0.11413 | 59.3 | 高橋 |
| 1.0 | 47757 | 0.113602 | 58.5 | |
| 1.2 | 26945 | 0.108935 | 52.0 | 田村 |
| 1.4 | 22998 | 0.107298 | 49.7 | 田村 |
| 1.5 | 17689 | 0.103750 | 44.8 | 根本 |
| 1.8 | 14668 | 0.102133 | 42.5 | 根本 |
| 2 | 13986 | 0.069684 | -2.8 | 藤原 |
| 4 | 3009 | 0.0487895 | -32.0 | 藤原 |
| 8 | 967 | 0.0764429 | 7.2 | 森島 |
| 10 | 558 | 0.0768385 | 6.7 | 森島 |
ヤング率:7500(N/mm^2) ポアソン比:0.4 理論値:0.0716667(mm)
12月4日課題†
| メッシュサイズ | 要素数 | 先端変位 | 相対誤差(%) | 計算者 |
| 0.8 | 226647 | 0.08053 | 56.9 | 高橋 |
| 0.9 | 127506 | 0.07678 | 49.7 | 高橋 |
| 1.0 | 92447 | 0.05276 | 2.79 | |
| 1.2 | 88386 | 0.05264 | 2.55 | 田村 |
| 1.4 | 78086 | 0.05261 | 2.49 | 田村 |
| 1.5 | 70032 | 0.072549 | 41.3 | 根本 |
| 1.8 | 34858 | 0.068375 | 33.2 | 根本 |
| 2 | 20313 | 0.063280 | 23.3 | 藤原 |
| 3 | 18229 | 0.0489236 | -4.68 | 君島 |
| 4 | 8067 | 0.050046 | -2.51 | 藤原 |
| 5 | 4846 | 0.036772667 | -28.3 | 君島 |
| 8 | 3814 | 0.0270877 | -47.2 | 森島 |
| 10 | 1716 | 0.0217906 | -57.5 | 森島 |
ヤング率(木材):7500(N/mm^2) ポアソン比(木材):0.4
ヤング率(鋼板):206000(N/mm^2) ポアソン比(鋼板):0.3
理論値:0.05133(mm)
春休みの課題†
幾何学非線形†
1000N†
鋼材を想定、荷重は1000N

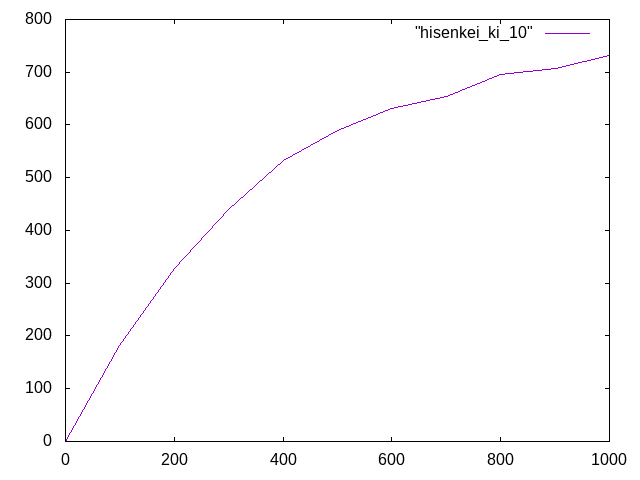
300N†
荷重300Nのときは線形に近いグラフの形になった。

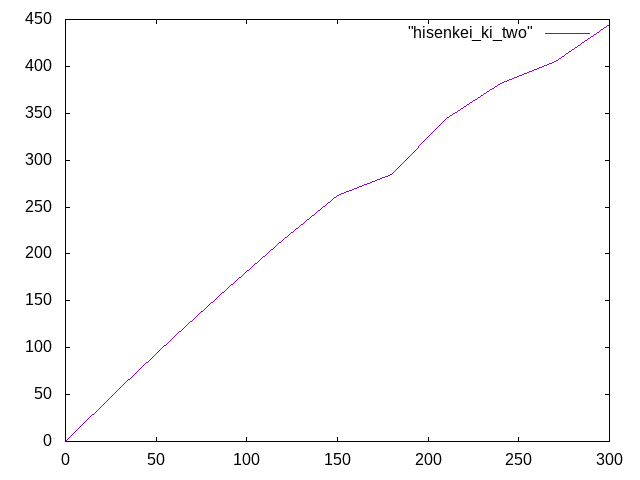
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)




