![[PukiWiki]](image/pukiwiki.png "[PukiWiki]")
| 日時 | 作業時間 | 作業内容 |
| 10/15 | 90分 | 顔合わせ |
| 10/21 | 30分 | タッチタイプ |
| 10/22 | 90分 | コマンド練習、タッチタイプ |
| 10/29 | 90分 | gnuplot練習 |
| 11/5 | 90分 | salome片持梁の解析 |
| 11/9 | 80分 | 片持梁の課題 |
| 11/12 | 90分 | salome単純梁の解析 |
| 11/17 | 60分 | 単純梁の課題 |
| 11/19 | 90分 | salome単純梁(異方)の解析 |
| 11/25 | 60分 | 単純梁(異方)の課題 |
ケーブル腐食を考慮した斜張橋のケーブル破断挙動に関する動的応答解析
ケーブル部を梁要素、桁をシェル要素でつくる
5月27日 橋桁、タワー完成
スイープと再番号付けまでは完了したので来週までにケーブルと梁ピン結合を終わらせる
作成のグラフ画像
片持梁の解析結果 片持梁の先端変位(集中荷重)の理論値 Pl^3/3EI
| メッシュ長さ | 要素数 | 先端変位 | 相対誤差 | 計算者 |
| 0.5 | 333932 | 6.564 | -1.54 | 新谷 |
| 0.7 | 218976 | 6.541 | -1.89 | 安部 |
| 0.9 | 71718 | 6.431 | -3.54 | 梅宮 |
| 1.2 | 33635 | 6.304 | -5.45 | 七五三 |
| 1.4 | 7699 | 6.316 | -5.26 | 柴田 |
| 1.5 | 4444 | 6.121 | -8.19 | 小池 |
| 1.8 | 2293 | 5.737 | -14.0 | 岩崎 |
| 2 | 2296 | 5.738 | -13.9 | 畠山 |
| 3 | 3487 | 5.474 | -17.9 | 新谷 |
| 4 | 1255 | 3.616 | -45.8 | 安部 |
| 5 | 516 | 4.824 | -27.6 | 岩崎 |
| 6 | 520 | 4.818 | -27.7 | 小池 |
| 7 | 339 | 1.412 | -78.8 | 七五三 |
| 8 | 183 | 4.041 | -39.4 | 柴田 |
| 9 | 191 | 4.002 | -40.0 | 畠山 |
| 10 | 596 | 3.463 | -48.1 | 梅宮 |
単純梁の解析結果 単純梁の変位の理論値 Pl^3/48EI
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 662117 | 0.429 | 2.89 | 新谷 |
| 0.7 | 145352 | 0.424 | 1.7 | 安部 |
| 0.9 | 105952 | 0.4235 | 1.68 | 梅宮 |
| 1 | 89494 | 0.420 | 0.719 | |
| 1.2 | 32647 | 0.405 | -2.83 | 七五三 |
| 1.4 | 36747 | 0.406 | -2.53 | 柴田 |
| 1.5 | 15675 | 0.396 | -5.04 | 小池 |
| 1.8 | 11493 | 0.394 | -5.5 | 岩崎 |
| 2 | 10495 | 0.395 | -5.09 | 畠山 |
| 3 | 2356 | 0.321 | -23.0 | 新谷 |
| 4 | 1470 | 0.330 | -20.9 | 安部 |
| 5 | 429 | 0.143 | -65.7 | 岩崎 |
| 6 | 355 | 0.125 | -70.0 | 小池 |
| 7 | 415 | 0.0997 | -76.1 | 七五三 |
| 8 | 109 | 0.124 | -70.3 | 柴田 |
| 9 | 91 | 0.135 | -67.7 | 畠山 |
| 10 | 237 | 0.0776 | -81.4 | 梅宮 |
今回、荷重の逆向きをy軸正としたので変位は負となり、グラフは右のようになった
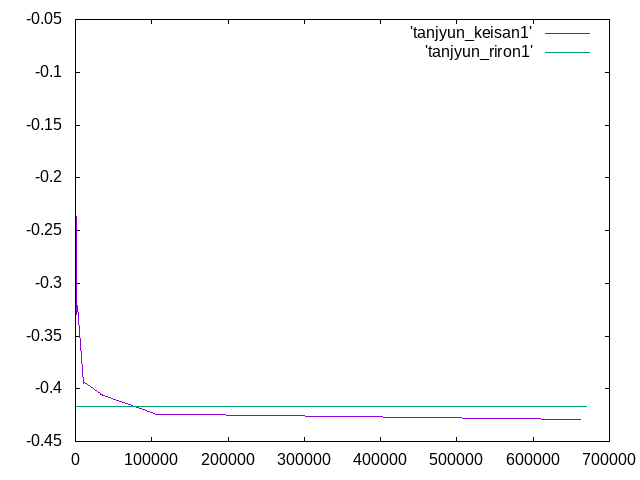
単純梁(異方)の解析結果 ティモシェンコ梁理論による変位の理論値 (PL^3/48EI)+(PL/4kGA)
・1次
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 939345 | 0.552 | 12.2 | 新谷 |
| 0.7 | 169112 | 0.540 | 9.76 | 安部 |
| 0.9 | 105952 | 0.537 | 9.15 | 梅宮 |
| 1.2 | 32647 | 0.518 | 5.29 | 七五三 |
| 1.4 | 17737 | 0.514 | 4.47 | 柴田 |
| 1.5 | 15675 | 0.511 | 3.86 | 小池 |
| 1.8 | 11710 | 0.507 | 3.05 | 岩崎 |
| 2 | 10495 | 0.506 | 2.79 | 畠山 |
| 3 | 3885 | 0.451 | -8.33 | 新谷 |
| 4 | 2311 | 0.447 | -9.14 | 安部 |
| 5 | 431 | 0.290 | -41.1 | 岩崎 |
| 6 | 347 | 0.341 | -30.7 | 小池 |
| 7 | 415 | 0.220 | -55.3 | 七五三 |
| 8 | 109 | 0.243 | -50.6 | 柴田 |
| 9 | 91 | 0.251 | -48.9 | 畠山 |
| 10 | 237 | 0.211 | -57.1 | 梅宮 |
・2次
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 939345 | 0.563 | 14.4 | 新谷 |
| 0.7 | 169112 | 0.567 | 15.2 | 安部 |
| 0.9 | 105952 | 0.565 | 14.8 | 梅宮 |
| 1.2 | 32647 | 0.555 | 12.8 | 七五三 |
| 1.4 | 17737 | 0.554 | 12.6 | 柴田 |
| 1.5 | 15675 | 0.552 | 12.2 | 小池 |
| 1.8 | 11710 | 0.551 | 12.0 | 岩崎 |
| 2 | 10495 | 0.549 | 11.6 | 畠山 |
| 3 | 3885 | 0.540 | 9.76 | 新谷 |
| 4 | 2311 | 0.535 | 8.74 | 安部 |
| 5 | 431 | 0.525 | 6.71 | 岩崎 |
| 6 | 347 | 0.527 | 7.11 | 小池 |
| 7 | 415 | 0.508 | 3.25 | 七五三 |
| 8 | 109 | 0.508 | 3.25 | 柴田 |
| 9 | 91 | 0.508 | 3.25 | 畠山 |
| 10 | 237 | 0.507 | 3.05 | 梅宮 |
| メッシュ長さ | 要素数 | 変位 | 相対誤差 | 計算者 |
| 0.5 | 652354 | 0.089 | -10.2 | 新谷 |
| 0.7 | 192792 | 0.09193 | -7.3 | 安部 |
| 0.9 | 104548 | 0.0919 | -7.26 | 梅宮 |
| 1.2 | 45045 | 0.09192 | -7.27 | 七五三 |
| 1.4 | 24237 | 0.0919 | -7.27 | 柴田 |
| 1.5 | 19998 | 0.0919 | -7.29 | 小池 |
| 1.8 | 12624 | 0.092 | -7.07 | 岩崎 |
| 2.0 | 10716 | 0.0919 | -7.29 | 畠山 |
| 3.0 | 6000 | 0.092 | -7.07 | 新谷 |
| 4.0 | 2993 | 0.09087 | -8.3 | 安部 |
| 5.0 | 1010 | 0.090 | -9.09 | 岩崎 |
| 6.0 | 836 | 0.0886 | -10.62 | 小池 |
| 7.0 | 1167 | 0.0865 | -12.741 | 七五三 |
| 8.0 | 284 | 0.0847 | -14.53 | 柴田 |
| 9.0 | 261 | 0.0832 | -16.1 | 畠山 |
| 10 | 607 | 0.0874 | -11.8 | 梅宮 |
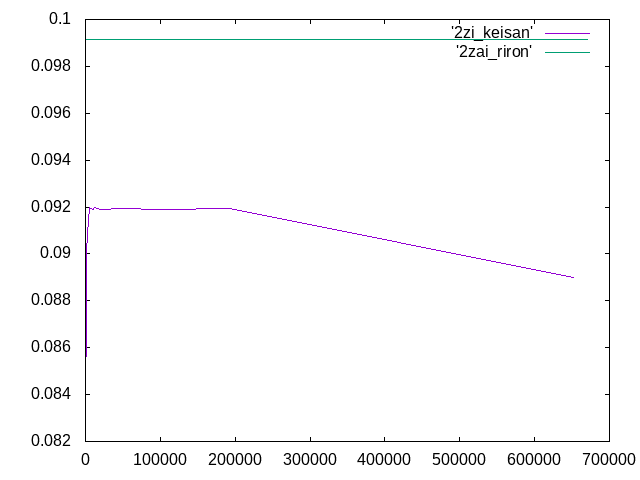2次で解析を行ったので、要素数が大きくなればなるほど理論値に収束する予想だったが、
過去のグラフに比べ、縦軸(変位)の間隔が細かいのでグラフが予想に反した形となった。
また、単純梁や張出梁と比較すると変位がかなり小さくなった。
