DAF†
- 関西道路研究会の定義
- 動的増幅率 \( DAF={\displaystyle \frac{S_{dyn}-S_{0}}{S_{stat}-S_{0}}} \)
- \( S_{dyn} \): 動的解析の最大応答値
- \( S_{stat} \): 静的解析の応答値
- \( S_{0} \): 初期値
1.854関係†
1自由度系の振動†
- 10. 振動論の基礎
(鬆徒労苦衷有迷禍荷苦痛)
- 動的増幅率\( M_{D} \)の定義は下記のDAFと同じ。強制振動数：\( p \), 固有振動数：\( \omega \)になってて、下記と逆だけど。
- \( {\displaystyle DAF=\frac{1}{\sqrt{\left(1-\frac{p^{2}}{\omega^{2}}\right)^{2}+(2\beta\frac{p}{\omega})^{2}}}} \)
- \( p=\omega \)のとき、\( DAF={\displaystyle \frac{1}{2\beta}} \) つまり、強制振動の振動数が固有振動数に一致すると共振し、減衰がなければ無限大。\( \frac{p}{\omega}\ll 1 \)なら\( DAF=1 \)
- 橋梁設計の荷重
(DAFの定義)この文献では、強制振動数：\( \omega \), 固有振動数：\( p \)
- \( {\displaystyle DAF=\frac{1}{\sqrt{\left(1-\frac{\omega^{2}}{p^{2}}\right)^{2}+(2h\frac{\omega}{p})^{2}}}} \)
- \( \omega=p \)のとき、\( DAF={\displaystyle \frac{1}{2h}} \) つまり、強制振動の振動数が固有振動数に一致すると共振し、減衰がなければ無限大。
剛体衝突による衝撃†
- 過渡振動(インパルス応答を積分してステップ応答を得る)
- 熊大機械
- 上記にのっている減衰ありのステップ応答は
\( x_{s}(t)={\displaystyle \frac{1}{k}\left\{1-e^{-pt}\left(\frac{p}{q}\sin qt+\cos qt\right)\right\}} \)
- これをステップ荷重1の静的応答\( \frac{1}{k} \)で割って、岩熊先生の表記で書き換えると
- \( DAF=1-e^{-\beta\omega t}(\beta\sin\omega t+\cos\omega t) \)
- ちなみに、\( \beta=0 \)のときは、\( DAF=1-\cos\omega t \)となるので、最大値は\( \omega t=\pi \)のときで\( DAF_{max}=2 \)
- \( \beta=0.05, \omega t=\pi \)を代入すると、\( DAF=1-e^{-0.05\pi}(0.05\sin\pi+\cos\pi)=1+e^{-0.05\pi}=1.85463599915323342929363 \)
- 四捨五入したら1.854ではなく1.855では？ もしかして1.854は上記の式からではなく数値的に求めた値？
- daf.f90
implicit real*8(a-h,o-z)
h=0.05d0
omg=1.d0
dafmax=0.d0
do i=0, 10000
t=real(i)/100.d0
u=1-exp(-h*omg*t)*(h*sin(omg*t)+cos(omg*t))
print*, t, u
if(u>dafmax) dafmax=u
end do
pi=acos(-1.d0)
print *, "# DAF_max=",dafmax
print *, "# 1+e^{-0.05π}=", 1.d0+exp(-0.05d0*pi)
end
みたいなプログラムを組んで、\( \beta=0.05, \omega=1 \)とかで回してみると、
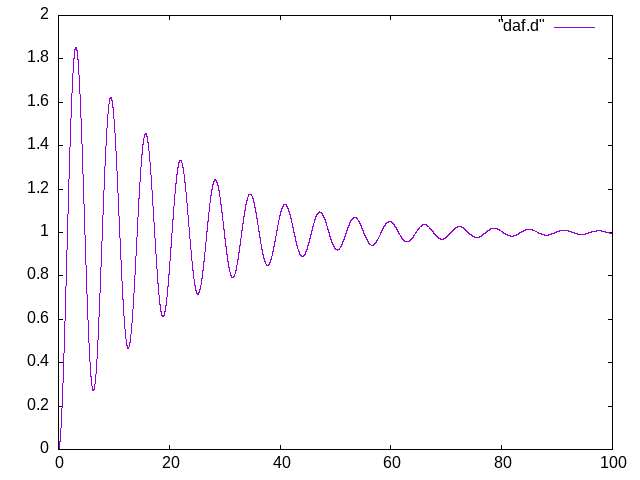
# DAF_max= 1.8546349124744650
# 1+e^{-0.05π}= 1.8546359991532335
\( \omega \)の値を大きくした場合は、
t=real(i)/100.
みたいに、時間きざみを細かくしてやらないと、1.8546から少しずれたところが求まる。
![[PukiWiki]](image/pukiwiki.png "[PukiWiki]")
