Introduction Into Design Engineering Week 10

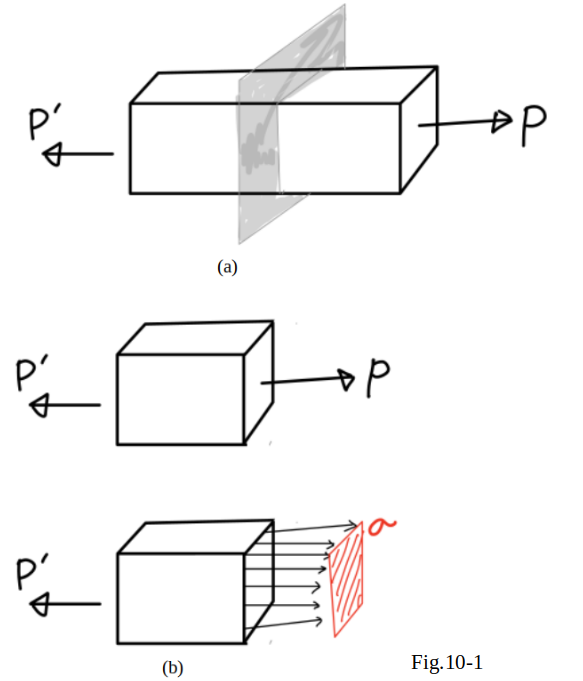In the previous sessions, axial force exerted on a two-force member (see in Fig.10_1(a)) were found to cause normal stress in that member (see in Fig.10_1(b)).
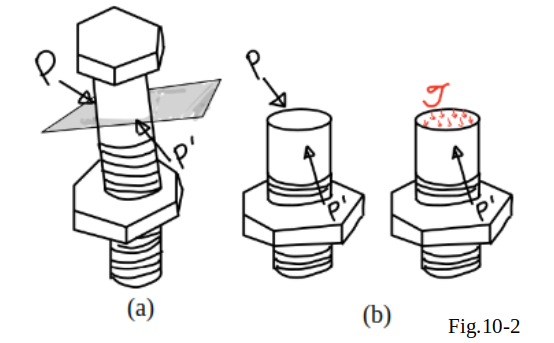
While transverse forces exerted on bolts and pins (Fig.10_2(a)) were found to cause shearing stresses in those connections(Fig.10_2(b)).
The reason such a relation was observed between axial forces and normal stresses on one hand, and transverse forces and shearing stresses on the other, was because stresses were being determined only on planes perpendicular to the axis of the member or connection.
As it will be seen in this section, axial forces cause both normal and shearing stresses on planes which are not perpendicular to the axis of the member.
Similarly, transverse forces exerted on a bolt or a pin cause both normal and shearing stresses on planes which are not perpendicular to the axis of the bolt or pin.

Consider the two-force member of Fig.10_1, which is subjected to axial forces P and P’.
If we pass a section forming an angle $\theta$ with a normal plane (Fig.10_3(a)) and draw the free-body diagram of the portion of member located to the left that section (Fig.10_3(b)), it would be found from the equilibrium conditions of the free body that the distributed forces acting on the section must be equivalent to the force P . Resolving P into components F and V , respectively normal and tangential to the section (Fig.10_3(c)), it should be;
$F = P \cos\theta$ ....(eq.10_1)
$V = P \sin\theta$ ....(eq.10_2)
The force F represents the resultant of normal forces distributed over the section, and the force V the resultant of shearing forces (Fig.10_3 (c) and (d)).
The average values of the corresponding normal and shearing stresses are obtained by dividing, respectively, F and V by the area $A_{\theta}$ of the section;
$\sigma = \frac{F}{A_{\theta}}$ ...(eq.10_3)
$\tau = \frac{V}{A_{\theta}}$ ...(eq.10_4)
Substituting for F and V from (eq.10_1) and (eq.10_2) into (wq.10_3) and (eq.10_4) respectively, and observing from Fig.10_3(c) that
$A_{0} = A_{\theta}\cos\theta$
or
$A_{\theta} =\frac{A_0}{\cos\theta}$
where $A_0$ denoted the area of a section perpendicular to the axis of the member.
These equations will be obtained
$\sigma = \frac{P\cos\theta}{A_0 / \cos\theta}$
$\tau = \frac{P\sin\theta}{A_0 / \cos\theta}$
or
$\sigma =\frac{P}{A_0}\cos^2{\theta}$ ...(eq.10_5)
$\tau =\frac{P}{A_0}\sin{\theta}\cos{\theta}$ ...(eq.10_6)

It should be noted from eq.10_5 that the normal stress $\sigma$ is maximum when $\theta =0$, i.e., when the plane of the section is perpendicular to the axis of the member, and that it approaches zero as $\sigma$ approaches $\theta =90°$.
The value of $\sigma$ should be checked when $\sigma =0$, it should be
$\sigma_{m}=\frac{P}{A_0}$ ...(eq.10_7)
as it is found earlier session.
The second of eq.10_6 shows that the shearing stress $\tau$ is zero for $\sigma =0$ and $\sigma =90°$, and that for $\sigma =45°$ it reaches its maximum value,
$\tau_{m}=\frac{P}{A_0}\sin45°\cos45°=\frac{P}{2A_0}$ ...(eq.10_8)
The equation 10_7 indicates that, when $\sigma =45°$, the normal stress $\sigma$’ is also equal to $\frac{P}{2A_0}$:
$\sigma’=\frac{p}{A_0}\cos^2{45°}=\frac{P}{2A_0}$ ...(eq.10_9)
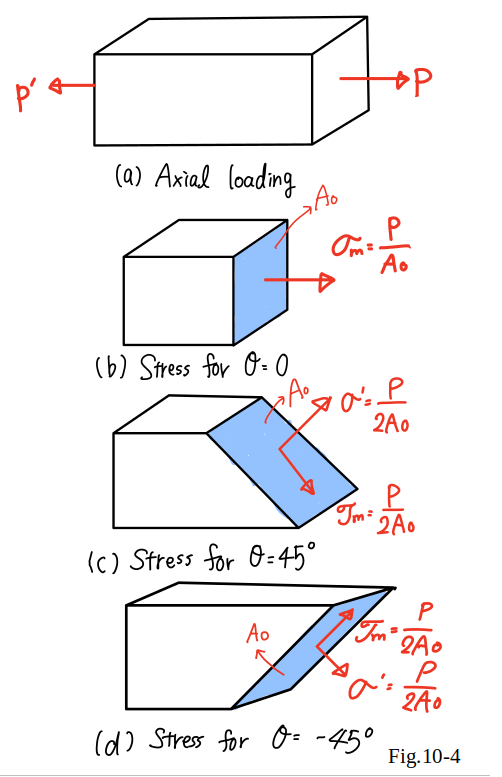
The results obtained in Eqs.(10_7), (10_8), and (10_9) are shown graphically in Fig.10_4.
It is noted that when the same loading may produce either a normal stress
$\sigma_{m}=\frac{P}{A_0}$
and no shearing stress (Fig.10_4(b)), or a normal and shearing stress of the same magnitude
$\sigma’=\tau=\frac{p}{A_0}$
(Fig.10_4 (c) and (d)), depending upon the orientation of the section.

Please go to the webclass and answer the question(s) shown in webclass.