卒論日誌†
| 日付 | 時間帯 | 作業時間 | 内容 | 立会 |
| 10/11 | 16:00-17:00 | 1.0 | 創造工房 | 後藤さん |
| 10/18 | 14:30-16:30 | 2.0 | 創造工房 | 後藤さん |
| 10/21 | 12:00-15:20 | 3.5 | 創造工房 | 高橋さん |
| 10/28 | 13:00-16:30 | 3.5 | 創造工房 | 高橋さん |
| 11/1 | 13:00-16:30 | 3.5 | 創造工房 | 後藤さん 他 |
| 11/6 | 12:00-13:00 | 1.0 | 創造工房 | |
| 11/8 | 14:30-16:00 | 1.5 | 創造工房 | 後藤さん |
| 11/22 | 14:30-16:00 | 1.5 | 創造工房 | 後藤さん高橋さん |
| 12/6 | 14:30-16:00 | 1.5 | 創造工房 | 後藤さん高橋さん |
| 12/20 | 14:30-16:00 | 1.5 | 創造工房 | 加藤さん、4年生のみなさん |
| 1/10 | 14:30-16:00 | 1.5 | 創造工房 | 後藤さん |
| 1/15 | 14:30-16:00 | 1.5 | 創造工房 | 後藤さん |
| 1/31 | 14:30-19:00 | 4.5 | 創造工房 | 後藤さん |
| 2/2 | 19:00-24:00 | 5.0 | 創造工房課題 | 後藤さん |
10/18課題†
たわみ理論値 6.66667
メッシュ0.5(佐藤)†
| たわみ実験値 | 相対誤差 | 要素数 |
| 6.57938 | -1.4% | 394121 |
メッシュ1(吉田)†
| たわみ実験値 | 相対誤差 | 要素数 |
| 6.443 | -3.4% | 72278 |
メッシュ2(梅田)†
| たわみ実験値 | 相対誤差 | 要素数 |
| 5.73825 | -13.9% | 11817 |
メッシュ4(青山)†
| たわみ実験値 | 相対誤差 | 要素数 |
| 4.94280 | -25.858% | 2862 |
メッシュ8(小川)†
| たわみ実験値 | 相対誤差 | 要素数 |
| 4.404 | -39.4% | 897 |
10/25課題†
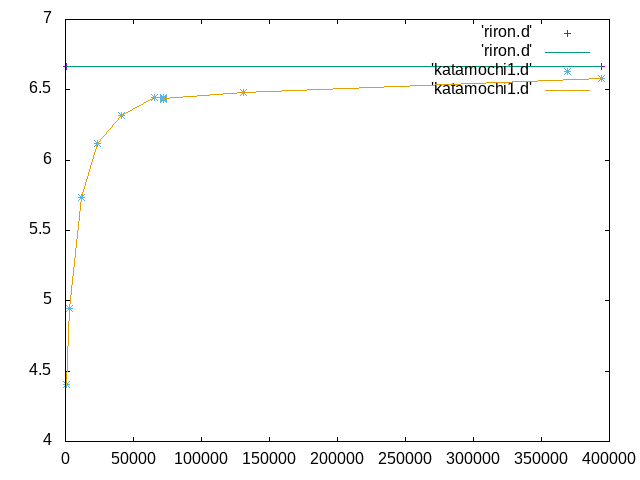
| メッシュ数 | 要素数 | 変位 | 相対誤差 | 作成者 |
| 8 | 897 | 4.404 | -39.4% | 小川 |
| 4 | 2862 | 4.943 | -25.9% | 青山 |
| 2 | 11817 | 5.738 | -13.9% | 梅田 |
| 1.8 | 11758 | 5.737 | -13.98 | 梅田 |
| 1.5 | 23417 | 6.121 | -8.23% | 梅田 |
| 1.4 | 41096 | 6.316 | -5.30% | 青山 |
| 1.2 | 65575 | 6.443 | -3.35% | 小川 |
| 1.0 | 72278 | 6.443 | -3.4% | 吉田 |
| 0.9 | 71718 | 6.431 | -3.53 | 吉田 |
| 0.8 | 72101 | 6.437 | -3.48 | 青山 |
| 0.7 | 130916 | 6.478 | -2.87% | 佐藤 |
| 0.5 | 394121 | 6.579 | -1.4% | 佐藤 |
メッシュ0.8,0.9,1.0で期待通りの数値が出なかった。原因はSalomeでメッシュを作る際にきれいな値でメッシュを割り切れず、切り上げされたなどが考えられる。他はグラフからも期待通りの結果が得られた。
11/1 課題†
理論値 0.41667
| メッシュ数 | 要素数 | 変位 | 相対誤差 | 作成者 |
| 2 | 20526 | 0.37063 | -11.05 | 佐藤 |
| 1.5 | 50359 | 0.41195 | -1.13 | 青山 |
| 1.0 | 62360 | 0.41651 | -0.037 | 梅田 |
| 0.8 | 199968 | 0.41646 | -0.050 | 吉田 |
| 0.5 | 322687 | 0.42877 | 2.9 | 小川 |
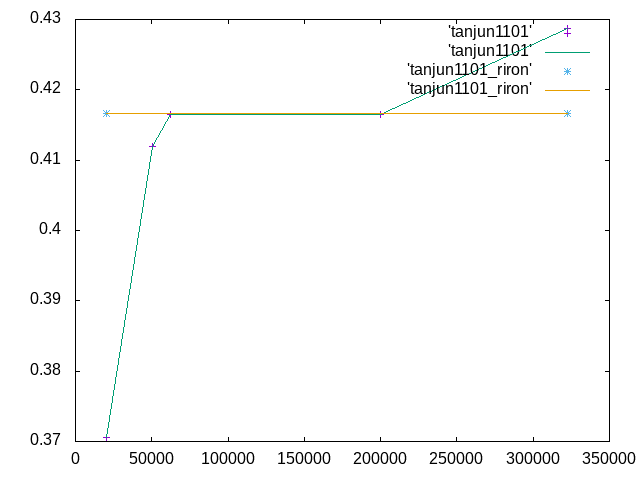
試験体ごとに最適なメッシュ長さ(要素数)があり、今回はメッシュ1.0が最も理論値に近い値になった。
プロット数が5つと少ないため、グラフが角ばった形状になった。より多くのメッシュ長さで試験をすることによってよりなめらかなグラフを得られるだろう。
11/8†
ティモシェンコ理論値 0.491668
初等理論値 0.41667
| メッシュ数 | 要素数 | 変位 | 相対誤差 | 作成者 |
| 2.0 | 20526 | 0.47657183 | -3.07 | 佐藤 |
| 1.8 | 28053 | 0.49266686 | 0.203 | 佐藤 |
| 1.5 | 50359 | 0.50010225 | 1.72 | 梅田 |
| 1.3 | 57455 | 0.50384356 | 2.48 | 青山 |
| 1.1 | 83278 | 0.50338136 | 2.38 | 小川 |
| 1.0 | 62360 | 0.50576873 | 2.87 | 青山 |
| 0.9 | 87953 | 0.51027538 | 3.78 | 小川 |
| 0.8 | | 0.51454371 | 0.465 | 吉田 |
| 0.5 | 322687 | 0.52149586 | 6.07 | 小川 |
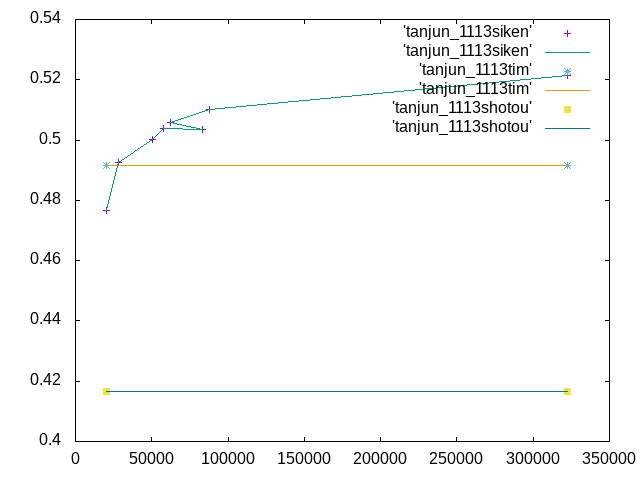
グラフを見ると、実験値と初等・ティモシェンコそれぞれの理論値を比較して、ティモシェンコの値の方が実験値と近い値になった。これは単純梁が異方性であることを示している。メッシュ1.8での相対誤差が最小になったため、この単純梁はメッシュ1.8で試験するのがよい。
11/22 課題†
| 拡大係数 | 要素数 | 変位 | 相対誤差 | 作成者 |
| 0.8 | 3657 | 5.5734 | -16.399 | 青山 |
| 0.7 | 4245 | 5.5717 | -16.425 | 吉田 |
| 0.6 | 7257 | 5.9119 | -11.322 | 梅田 |
| 0.5 | 13741 | 6.03154 | -9.527 | 小川 |
| 0.4 | 23349 | 6.26413 | -6.058 | 佐藤 |
| 0.3 | 57431 | 6.42253 | -3.662 | 全員 |
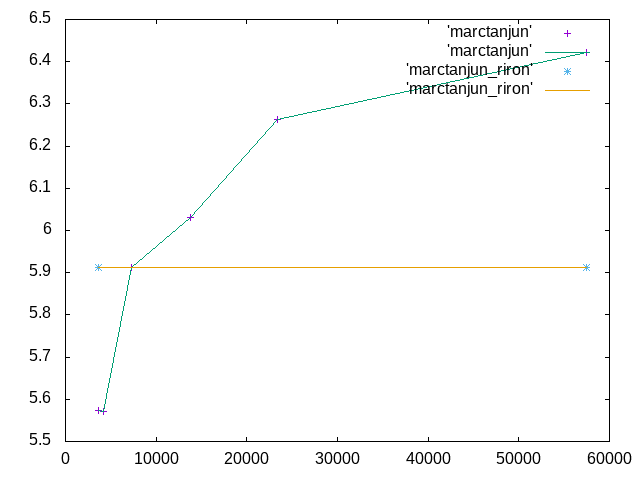
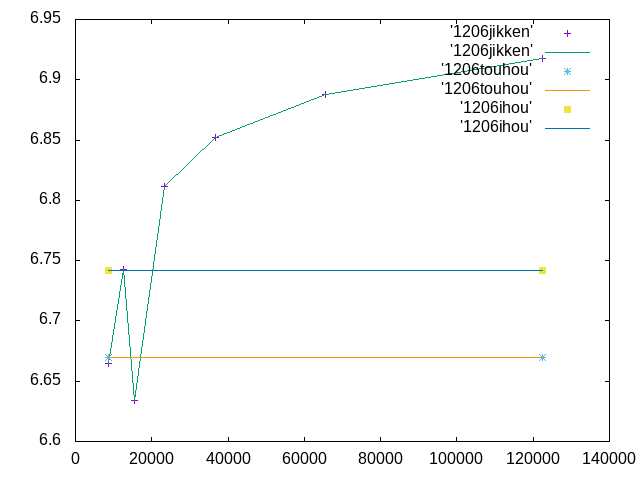
12/6 課題†
| 拡大係数 | 要素数 | 変位 | 相対誤差 | 作成者 |
| 0.8 | 122515 | 6.91749 | 2.6% | 吉田 |
| 1.0 | 65490 | 6.8877 | 2.2% | 梅田 |
| 1.2 | 36693 | 6.8519225 | 1.6% | 梅田 |
| 1.4 | 23341 | 6.8117175 | 1.0% | 吉田 |
| 1.6 | 15371 | 6.6336 | -1.6% | 小川 |
| 1.8 | 12480 | 6.74258 | 0.014% | 佐藤 |
| 2.0 | 8589 | 6.66499 | -0.011% | 梅田 |
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)