![[PukiWiki]](image/pukiwiki.png "[PukiWiki]")
・破断したボルトの順番ははっきりとはわからないが、ねじ山つぶれているボルトから破断したのではないか?
・短いボルトは最後まで頑張っていたのではないか？
・ボルトが緩んでいたらプレートが浮き上がってボルト破壊
・繰り返し破断
・ねじ山なくなる
1,サグモデル
両端固定にして自重をかけることで張力導入できる。
この方法により、斜めにしても張力導入でき、固定点間距離を一定にして解析できる。
2,ケーブルを１本ではなくストランドでモデル化してはどうか？
ストランドが束なったモデルと１本の円柱モデルでの比較
・被覆は、直接ケーブルにポリエチレンを溶かしながら覆っていくため、ケーブルと被覆の間には空間はない。
・基本的に被覆の厚さはケーブルの種類(直径・本数)で決まっている。
・レインバイブレーションは風速が10数m/s以上で発生しづらくなる。
→水道が破壊されてしまうから。
・張力測定に用いられる高次振動法における振動数と振動モードの対応関係は、架設時に測定しておく
これまでのサグは、ケーブルモデルを真っ直ぐに作成し重力を与えてサグを作っていたが、この方法だとサグによる影響が出ていない可能性がある。
そこで、モデル作成時にサグの形状に曲げて作っておき、張力を与え、その後重力を載荷することでサグを形成させるという手順で解析を行う。
ある一定のサグ比になると、サグなしモデルと比較して固有振動数が変化するという論文もあるので、まずはサグを作った状態で振動解析を行う。
サグモデルを作成するために、ケーブル直線モデルに張力と重力をかけてサグを作り、各点の座標を読み取る。
その座標に従ってgeometryで点を打ち、曲線状にケーブルを作成する。
l=113.149m、d=152mm、T=1003.69kN、ρ=7800kg/m^3、ポアソン比=0.3のときのサグの理論値は2.16m
直線モデルに張力&重力をかけた時のサグの大きさは2.25m(理論値との相対誤差は4.2%)
卒論ではSolid要素を使用して振動解析を行っていたが、今後はcable要素を使っていく予定であるためcable要素でも振動解析を行えるかを確認してみる。
①step数0.001での振動解析
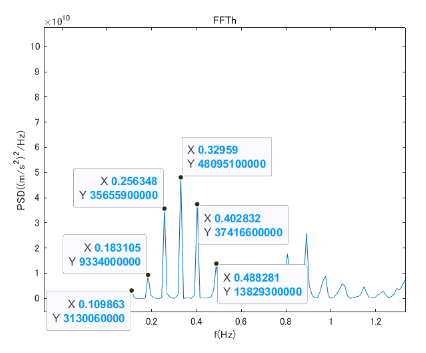
固有振動数の理論値は、1次=0.38Hz、3次=1.13Hz、5次=1.88Hz
どの卓越振動数がどのモードのものかがわからないようなグラフになっている。もしかしたら、step数の影響で雑音が入っているかも
②step数0.01での振動解析
step数0.001のときに出ていた雑音のような卓越振動数がなくなり、理論値に近い値が出力されている。
また、solid要素で解析していたときは、1次=0.391Hz、3次=1.17Hz、5次=2.05Hzであり、それにも近い値が出力されるようになった。
③直線モデルで重力かけない(サグを作らない状態で)振動解析を行った結果が下の表 step数0.01
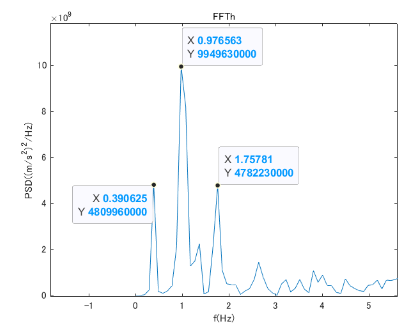
3次と思われる卓越振動数以外は、重力ありの振動解析と同じ振動数になっている。
次はsin波をあたえて卓越振動数で共振するかを確認する。
振動解析で卓越した振動数のsin波を与えて共振するか確認する。
モデルには重力をかけない状態でsin波を与えている。
0.390625Hzのsin波
1.07422Hzのsin波
1.75781Hzのsin波
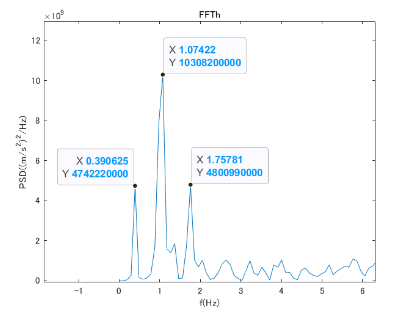
この結果から、由利橋のケーブルの固有振動数は1次モード=0.390625Hz、3次モード=1.07422Hz、5次モード=1.75781Hzであることがわかった。
理論値との誤差は、1次モード=3.7%、3次モード=5.3%、5次モード=6.4%
卒論ではsolid要素(3D)で振動解析を行っていたが、cable要素(1D)でも振動解析を行えることがわかったので、次はサグモデルを作成していきたい。
5/2〜5/7 主塔側のプレートとボルトのモデル化完了
→エラー出ない。
5/8～5/11 桁側のプレートとボルトのモデル化完了
→エラー出ない。
5/12～ ケーブルのモデル化作成
→接点を共有させて問題なく解析できるか確認していく。
5/22〜 モデルのmesh
→被覆部分のmesh部分でエラーが起きてしまい色々試している。
要素数が大きくなってしまっている。
主塔側のモデル
桁側のモデル
5/29〜 モデル完成(被覆部分はmeshを切れなかったため、まずはケーブルには被覆をつけない状態)
LIAISON_MAILを使って各部材を結合したところ、エラー出ずに問題なく行うことができた。(結合の仕方はOK)
3DModelでサグを再現する設定がまだ見つけられておらずケーブルは直線にしている。
6/1〜 重力のみ考慮
今回のモデルに重力を考慮したところ、ケーブル部分のZ方向最大変位は1.15mであった。(この点でのx方向変位は0.51mであり、xz方向の変位量は1.26m)
保護管長106.367m、張力1003.69kNのときのサグの理論値は1.95m
この点では、SIGMxx=36.8MPa、SIGMzz=6.9MPaであり、軸力は37.4MPaとなり、目標の値より小さくなっている。(1003.69kNは55.3MPa)
3Dでサグモデルの作成前に両端固定したまま張力導入する方法を模索
PRE_SIGMコマンドは動的解析には使えないので２段階解析で適用してみる。(1段階目に静的でPRE_SIGM、2段階目に動的解析でインパクト)
両端固定した状態の結果をFFTにかけたところ、3.91Hz、7.12Hz、11.13Hzで卓越した(sin波を与えないとモード数との関係がわからない。)
卒論のときのFORCE_FACEで与える方法のときはf1=2.93Hz,f3=8.60Hz,f5=13.96Hzであった。
塔の固有振動数を求めるためにモーダル解析を行った。
・面内振動
1次=1.465Hz 3次=5.786Hz 5次=15.744Hz
・面外振動
1次=0.668Hz 3次=4.137Hz 5次=11.471Hz
下の一時的なエラーがたくさん出て、フリーズしてしまう。
収束エラーが出てしまっているので原因を見つけていきたい
モデルは塔、プレート、ボルト、保護鋼管を使って時刻歴解析を行う。
最初の解析では、載荷場所は保護鋼管の先端にして、静的に載荷していく。
ボルトにどのような力が働いているかを様々な仮定の下、手計算していく。
プレートに面外モーメントが発生した時に軸力変動
仮定1 : 16本のボルトでモーメントを受け持つとき
ボルトはM16 有効断面積は157mm^2
SS400 引張強さ=400N/mm^2×157mm^2=62.8kN
①強度区分が4.6の時 Bolt1,4が破断するときのケーブル中央の最大変位(一番破断しやすいボルト) 初期軸力=0.7×240×157=26.4kN 破断までの軸力変動=62.8-26.4=36.4kN ボルトに36.4kNの軸力変動があったときのケーブル固定部のモーメントM=Fi・∑ri^2/r (Fi：引張力、∑r^2：引張力が発生する全ボルトのモーメント中心からの距離の2乗和、ri：ボルトiのモーメント中心からの距離) =36.4×841821.28/348.65=87888.41kN・mm このモーメントが発生するときのケーブル中央の最大変位=12.2m ケーブル中央が12.2mの振幅があればボルト破断(1番危険な時を想定)
➁強度区分が4.8の時 Bolt1,4が破断するときのケーブル中央の最大変位(一番破断しやすいボルト) 初期軸力=0.7×320×157=35.2kN 破断までの軸力変動=62.8-35.2=27.6kN ボルトに36.4kNの軸力変動があったときのケーブル固定部のモーメント=27.6×841821.28/348.65=66640.66kNmm このモーメントが発生するときのケーブル中央の最大変位=9.25m ケーブル中央が9.25mの振幅があればボルト破断(1番危険な時を想定)
③7/29 「ボルトの強度計算の方法」を参考にした計算 (強度区分は4.6で計算) Bolt1,4が破断するときのケーブル中央の最大変位(一番破断しやすいボルト) 初期軸力=0.7×240×157=26.4kN 破断までの軸力変動=62.8-26.4=36.4kN ・「ボルト本数が増えても、ボルト1本あたりの負荷できる荷重は減少する」ということを考慮する(記事には、安全率が2となるボルト1本あたりの荷重は、ボルト1本では20824N、ボルト16本では4775Nである。)この値を参考にすると、36.4kN×(4775/20824)=8346.62Nの軸力変動で破断~ ボルトに846.62Nの軸力変動があったときのケーブル固定部のモーメントM=Fi・∑ri^2/r (Fi：引張力、∑r^2：引張力が発生する全ボルトのモーメント中心からの距離の2乗和、ri：ボルトiのモーメント中心からの距離) =8346.62×841821.28/348.65=20153054.16Nmm このモーメントが発生するときのケーブル中央の最大変位=2.80m ケーブル中央が2.80mの振幅があればボルト1番が破断(1番危険な時を想定)
仮定2 : 4本のボルト(Bolt1,4,9,12)だけで固定されているとき
ボルトはM16 有効断面積は157mm^2
SS400 引張強さ=400N/mm^2×157mm^2=62.8kN
①強度区分が4.6の時 Bolt1,4が破断するときのケーブル中央の最大変位(一番破断しやすいボルト) 初期軸力=0.7×240×157=26.4kN 破断までの軸力変動=62.8-26.4=36.4kN ボルトに36.4kNの軸力変動があったときのケーブル固定部のモーメントM=Fi・∑ri^2/r (Fi：引張力、∑r^2：引張力が発生する全ボルトのモーメント中心からの距離の2乗和、ri：ボルトiのモーメント中心からの距離) =36.4×243116.82/348.65=25381.89kN・mm このモーメントが発生するときのケーブル中央の最大変位=3.52m ケーブル中央が3.52mの振幅があればボルト破断(1番危険な時を想定)
・サビの量・場所がボルトごとに異なる。
→それによる影響がボルトごとに異なるため、段階的に破断した？
・座面が曲がっている。
→軸力だけの影響で破断したのだとしたら曲がる？
・破断面付近のねじ山がつぶれている
→断面欠損
・ボルトに赤くなっている部分がある。
→おそらく摩耗によるものだと思うが、なぜ赤なのか？
・破断後のボルトの長さが異なる。
7/28 ねじ締結体の疲労破壊対策 https://navi.hardlock.co.jp/column/%E9%87%91%E5%B1%9E%E3%81%AE%E6%90%8D%E5%82%B7%E3%81%AB%E3%81%A4%E3%81%84%E3%81%A6%E3%80%80%E3%80%8C%E7%96%B2%E5%8A%B4%E7%A0%B4%E5%A3%8A%E3%80%8D%E3%81%9D%E3%81%AE%EF%BC%93/
7/29 ボルトの強度計算の方法 https://www.rt-designlab.com/bolt_kyoudo_keisan.pdf
G1側のタワーとケーブルの変位 ケーブルの分割数は1
G2側のタワーとケーブルの変位
現在の問題点
反力が設計反力と一致しない。
全ケーブルの分割数を2にして固有値解析を行い、塔の固有振動数を求めた。
解析はエラーなく終わったため、以前出ていたエラーはケーブル分割によるものではなさそう。
塔の橋軸直角方向の振動数は0.80Hz
塔の橋軸方向の振動数は1.40Hz
この段階での問題点
・ケーブル分割数を増やすと、今のところ不安定になり解析ストップしてしまう。（7/15 解決）
・ケーブル張力が入らない。(一応、静的解析では解決。)
ケーブルの分割数を10mごとに1点の間隔で分割し、塔と桁の交差部に塔の固有振動数のsin波を与えた。ただし、現在の所ケーブルに張力は与えられていない。
塔とともに、ケーブルも橋軸直角方向の振動になった。
最初はひずみエネルギー比例減衰で解析をしていたが、その減衰方法だと各部材ごとの減衰係数が決まってしまい構造全体で同じ減衰にならないため、レイリー減衰でないと結果が正しく表示されないことがわかった。
この振動は倍率を上げている。
ケーブルの要素をつくるときに与えるプレストレスだと構造不安定でエラーが出てしまう。
それで張力を指定する以外に、「プレテンション荷重」で各ケーブルに張力を指定した。
しかし、「プレテンション荷重」では、荷重ケースや静的荷重に他の荷重(死荷重など)があると初期張力が入らない。
現在の問題点
・「プレテンション荷重」では荷重ケースや静的荷重に他の荷重(死荷重など)があると初期張力が入らない。
・幾何学的非線形を有効にしないと初期張力として入らないため、動的解析に移行できない。(現段階では、動的解析を幾何学的非線形ありで行う方法が見つけられていない)
ケーブル分割数を10mごとに1point
