まとめと考察†
※もし今後似たような研究をする人がいた時、少しでも参考になれば。
- kがおかしくなるパターン
- スパンを伸ばしすぎる
- 正方形断面の板厚を矩形断面に近いくらい厚くする
- 板厚がかなり厚い状態でヤング率を大きくする。
- オンサイト木橋断面の鉛直部材のみを厚くする。
- つまり、水平部材はせん断変形にあまり関係しないと仮定すれば
- せん断変形が小さくなるとkが合わなくなるということになる。
- これはFEMのたわみから逆算したkの式を見れば、そりゃそうだろ。っていう感じなんですが、
- Bankの言う「薄肉断面で適用可能」つまり「厚肉断面で適用できない」というのは、板厚がどうこうって言うよりも、ただ単に「せん断変形が小さすぎるとBankのkは使えない」っていうだけの話なんじゃないか?
- ってちょっと思いました。
- (水平部材のみを厚くしてもkは適用できるっていうのは「薄肉断面で適用可能」っていうのに矛盾しているから。)
- これが正しければ、Bankのkの適用範囲外にある断面は、箱断面であっても、単純に初等梁梁理論が合うっていうことになるかも。
卒論発表†
- 概要 1/28提出
- スライド 2/1提出
- 発表練習 1/25の週からできた人から
注意事項†
- スパンは\ellで表記(リットルみたいなl)
- バックアップをとる
- 実験の写真はk2のgakusei/syasin/2015へ保存
当面の目標と達成状況†
12/11時点での目標†
- 前回の解析を木材のE,G基準でやり直し(硬すぎてせん断補正係数が正しく測れていない?)
- 両方異方性の2種材料を解くプログラムを作る
12/4時点での目標†
- G1=G2でE1A1=E2A2,E1=E2でG1E1=G2E2となるように比較
11/24時点での目標†
- 剛性が近いほうがkが合う?
- ヤング率,せん断弾性係数を変え、厚さを変えてkを比較
- 鋼材を基準にする
11/17時点での目標†
- CowperのkとBankの1種材料のkはほぼ同じになった→もっと式変形してみる
- 今までのたわみの相対誤差のグラフをk(FEMから逆算したもの,Bank及びCowoerのもの)のグラフに書き換える。
11/14時点での目標†
- Bankのkで等方性材料を考える→Cowperのkと同じ式になるのか。
- 違う式になった場合、cowperとBankそれぞれで等方性を解き、相対誤差を比較。
10/30時点での目標†
- Cowperのせん断補正係数算定断面のbとhは肉厚間距離じゃないのか
→nとmを1にして検証 10/30 2つのcowoerのkが一致,肉厚間距離で解ける
- 箱断面を厚くしていってFEMのkとどれくらい合うか検証
10/2時点での目標†
- 箱の断面を変えて理論値と収束するか確かめる。
- Cowperによる長方形断面のkと正方形断面のkを比較
- 解析を効率化するプログラムを作る
- ファイルからたわみを読み込み、相対誤差を求めるプログラムを作った。また、2つのkによる相対誤差の比較を行った所、正方形断面では正方形断面のkのほうが誤差が小さい。
夏休み中の課題†
- 単純梁のkを推定
- 箱桁のたわみを推定
- 箱桁のkを推定
- 7/6
- 達成状況
- 異方性材料の設定で等方性材料を解くと誤差0.1%に収まる。
- 異方性材料を解く際、ヤング率とポアソン比の入れ方が分からない。
- 次回までの目標
- とりあえずヤング率を2種類にして、3通りのポアソン比の入れ方(上三角,下三角,3つだけ)で検証。手計算と近くなるか。
- 6/29
- 達成状況
- ポアソン比は0.49を超えると急に増大,0.33で誤差がほぼない。
- スパンを変えての比較は相対誤差が概ね2%以内に留まった。
- 次回までの目標
- 木材(直交異方性材料)についてFEMとティモシェンコ梁での比較をやれるところまで。
- 6/22
- 達成状況
- スパンを変えて片持ち梁についてFEMとティモシェンコで比較を行ったが、スパンを長くしていくと、長さが原因?と見られるエラーがでた。
- ポアソン比を0.499にして解析を行ったところ、FEMとティモシェンコの誤差が20%近くなった。
- 次回までの目標
- エラーの解決,あと何点かで比較。
- 断面、長さ一定でポアソン比を変えて比較。
- 6/15
- 次回までの目標
- salomeで簡単な梁(とりあえず単純梁)のモデルを作り、たわみについてFEMとティモシェンコ梁理論で比較。
卒論日誌†
| 日付 | 時間帯 | 作業時間(hr) | 内容 | 立会 |
| 4/9 | 17:30~20:30 | 3 | 構造力学 | |
| 4/10 | 16:00~18:00 | 2 | 構造力学 | |
| 4/10 | 18:00~19:00 | 1 | タイピング練習 | |
| 4/15 | 20:00~22:00 | 2 | 構造力学 | |
| 4/23 | 21:00~22:00 | 1 | vi練習 | |
| 4/30 | 10:00~12:00 | 2 | salome練習 | |
| 4/30 | 13:00~14:00 | 1 | 文献調べ | |
| 4月合計 | 12 | | |
| 5/8 | 9:00~11:00 | 2 | salome練習 | |
| 5/19 | 16:00~17:00 | 1 | salome練習 | |
| 5/20 | 12:00~15:00 | 3 | glmageReader+resseract-ocr-jpnのインストール | |
| 5/20 | 15:00~16:00 | 1 | 文献のOCR作業 | |
| 5月合計 | 7 | | |
| 6/14 | 18:00~22:00 | 4 | salome課題 | |
| 6/15 | 8:00~12:00 | 4 | salome課題 | |
| 6/16 | 13:00~16:00 | 3 | salome課題 | |
| 6/21 | 8:00~12:00 | 4 | FEMとTimoshenko梁のたわみ比較 | |
| 6/24 | 8:00~12:00 | 4 | ポアソン比を変えての比較 | |
| 6/24 | 19:00~21:00 | 2 | Fortran | |
| 6/28 | 16:30~19:30 | 3 | 長さを変えての比較 | |
| 6/30 | 13:00~17:00 | 4 | 直交異方性の解析 | |
| 6月合計 | 28 | | |
| 7/1 | 15:00~17:00 | 2 | 直交異方性の解析 | |
| 7/4 | 20:00~21:00 | 1 | 文献調査 | |
| 7/26 | 19:00~21:00 | 2 | 直交異方性の解析 | |
| 7月合計 | 5 | | |
| 8/9 | 13:00~16:00 | 3 | せん断補正係数の推定 | |
| 8/24 | 17:00~22:00 | 5 | せん断補正係数の推定 | |
| 8/25 | 17:00~22:00 | 5 | salome | |
| 8/27 | 8:00~16:00 | 8 | 橋の見学(山形県きごころ橋など) | |
| 8/28 | 10:00~12:00 | 2 | プログラム練習 | |
| 8/28 | 13:00~20:00 | 7 | プログラム練習 | |
| 8/29 | 10:00~12:00 | 2 | プログラム練習 | |
| 8/29 | 13:00~20:00 | 7 | プログラム練習 | |
| 8/30 | 9:00~12:00 | 3 | プログラム練習 | |
| 8/30 | 13:00~17:00 | 4 | プログラム練習及び解析 | |
| 8/31 | 10:00~12:00 | 2 | プログラム練習 | |
| 8/31 | 15:00~18:00 | 3 | 解析 | |
| 8月合計 | 51 | | |
| 9/1 | 14:00~20:00 | 6 | プログラムでl型断面を作る(箱断面の練習) | |
| 9/2 | 8:00~16:00 | 8 | 橋の見学(岩手県きききの吊り橋) | |
| 9/3 | 14:00~24:00 | 10 | プログラムで箱断面を作る | |
| 9/4 | 10:00~12:00 | 2 | 箱断面の作り方復習 | |
| 9/8 | 15:00~20:00 | 5 | 解析 | |
| 9/9 | 13:00~20:00 | 7 | 解析 | |
| 9/9 | 13:00~18:00 | 5 | 解析 | |
| 9/16 | 13:00~18:00 | 5 | 解析 | |
| 9/17 | 13:00~21:00 | 8 | 解析 | |
| 9/19 | 10:00~12:00 | 2 | Tex | |
| 9/19 | 13:00~18:00 | 5 | 解析 | |
| 9/20 | 8:00~18:00 | 10 | 解析及びTex | |
| 9/21 | 12:00~20:00 | 10 | Tex及びgnuplot | |
| 9/22 | 10:00~12:00 | 2 | gnuplot及びXfig | |
| 9/22 | 13:00~19:00 | 6 | Tex | |
| 9/23 | 18:00~22:00 | 4 | Tex | |
| 9/24 | 10:00~12:00 | 2 | スライド作成 | |
| 9/24 | 13:00~19:00 | 6 | スライド作成 | |
| 9/28 | 15:00~18:00 | 3 | 発表準備 | |
| 9/29 | 13:00~16:00 | 3 | 中間発表及びプログラム | |
| 9/30 | 10:00~12:00 | 2 | linux勉強 | |
| 9/30 | 13:00~20:00 | 7 | プログラム | |
| 9月合計 | 118 | | |
| 10/1 | 12:45~19:45 | 7 | プログラム | |
| 10/2 | 9:30~11:30 | 2 | プログラム | |
| 10/2 | 15:00~17:00 | 2 | 解析 | |
| 10/4 | 13:00~15:00 | 2 | 解析 | |
| 10/11 | 20:00~24:00 | 4 | 解析 | |
| 10/27 | 11:00~19:00 | 8 | 高さを変えてkの逆算 | |
| 10/29 | 18:00~22:00 | 4 | せん断補正係数のプログラム | |
| 10/30 | 9:00~13:00 | 4 | 高さを変えてcowperのkを算定 | |
| 10/30 | 15:00~18:00 | 3 | 高さを変えてcowperのkを比較 | |
| 10月合計 | 36 | | |
| 11/1 | 9:00~12:00 | 3 | 厚さを変えて自動計算するプログラム | |
| 11/1 | 13:00~20:00 | 7 | 解析 | |
| 11/5 | 16:00~19:00 | 3 | 2種材料のプログラム | |
| 11/6 | 13:00~16:00 | 3 | 厚さを変えて自動計算するプログラム | |
| 11/7 | 21:00~22:00 | 1 | 厚さを変えて自動計算するプログラム(0.1mm単位) | |
| 11/9 | 13:00~20:00 | 7 | 2種材料のプログラム | |
| 11/10 | 20:00~21:00 | 1 | 厚さを変えて計算(2種材料) | |
| 11/11 | 9:00~11:00 | 2 | 厚さを変えて計算(2種材料) | |
| 11/11 | 13:00~20:00 | 7 | プログラム | |
| 11/12 | 8:00~11:00 | 3 | 厚さを変えて計算(2種材料) | |
| 11/13 | 15:00~17:00 | 2 | Bankのkで1種材料を解く | |
| 11/17 | 10:00~15:00 | 5 | 1種材料のBankのkとCowperのkを比較 | |
| 11/18 | 12:00~15:00 | 3 | Bankのkを計算 | |
| 11/19 | 13:00~16:00 | 3 | 解析 | |
| 11/20 | 22:00~23:00 | 1 | プログラム | |
| 11/23 | 10:00~15:00 | 5 | 逆算したkとBankのkを比較 | |
| 11/24 | 12:00~17:00 | 5 | プログラム | |
| 11/26 | 13:00~22:00 | 9 | PC整備、解析 | |
| 11/27 | 15:00~19:00 | 4 | せん断弾性係数の違いによるkの比較 | |
| 11/28 | 10:00~12:00 | 2 | プログラム | |
| 11/28 | 13:00~17:00 | 4 | せん断弾性係数の違いによるkの比較 | |
| 11/30 | 12:00~18:00 | 6 | せん断弾性係数の違いによるkの比較 | |
| 11月合計 | 86 | | |
| 合計 | 343 | | |
| 12/3 | 12:00~16:00 | 4 | データ整理、グラフ作成 | |
| 12/4 | 18:00~22:00 | 4 | プログラム | |
| 12/5 | 13:00~18:00 | 5 | プログラム | |
| 12/6 | 12:00~13:00 | 1 | 解析 | |
| 12/7 | 17:00~18:00 | 1 | 解析 | |
| 12/8 | 22:00~23:00 | 1 | 解析 | |
| 12/9 | 17:30~18:30 | 1 | データ整理 | |
| 12/10 | 19:30~20:30 | 1 | グラフ作成 | |
| 12/16 | 12:00~21:00 | 9 | グラフ作成、Tex | |
| 12/17 | 12:00~17:00 | 5 | グラフ作成、Tex | |
| 12/18 | 20:00~22:00 | 5 | プログラム作成 | |
| 12/19 | 11:00~15:00 | 4 | スライド作成 | |
| 12/21 | 12:00~16:00 | 5 | スライド作成、発表練習 | |
| 12/22 | 10:00~15:00 | 4 | 中間発表 | |
| 12月合計 | 50 | | |
| 合計 | 393 | | |
| 1/5 | 16:00~18:00 | 2 | 解析 | |
| 1/8 | 10:00~17:00 | 6 | 解析 | |
| 1/12 | 11:00~18:00 | 6 | 解析 | |
| 1/13 | 9:00~17:00 | 7 | 解析 | |
| 1/14 | 9:00~21:00 | 12 | 解析、卒論概要 | |
| 1/15 | 1:00~6:00 | 5 | 解析、スライド | |
| 1/15 | 9:00~14:00 | 5 | 解析 | |
| 1/18 | 10:00~17:00 | 6 | スライド、概要 | |
| 1/19 | 10:00~15:00 | 4 | スライド、概要 | |
| 1/20 | 10:00~16:00 | 5 | スライド、概要 | |
| 1/21 | 10:00~15:00 | 4 | スライド、概要 | |
| 1/22 | 10:00~15:00 | 4 | スライド、概要 | |
| 1/24 | 10:00~15:00 | 4 | スライド、発表練習 | |
| 1/25 | 10:00~16:00 | 5 | スライド、概要 | |
| 1/25 | 10:00~16:00 | 5 | スライド、概要 | |
| 1/25 | 10:00~16:00 | 5 | スライド、概要 | |
| 1/26 | 12:00~20:00 | 8 | 発表練習、スライド | |
| 1/27 | 9:00~17:00 | 7 | 発表練習、スライド | |
| 1/28 | 9:00~17:00 | 7 | 発表練習、スライド | |
| 1/29 | 9:00~17:00 | 7 | 発表練習、スライド | |
| 1/30 | 9:00~17:00 | 7 | 発表練習、スライド | |
テーマ†
3Dで箱桁のせん断弾性係数の測定
Cowperのせん断補正,11/20,22:00~23:00,1,プログラム,係数は、箱断面になると極端に小さくなったりするが、それを測定できないだろうか。長谷川さんが木材で卒論でやったことを3D材料でやり直し。
プログラム†
箱断面の厚さを変えて逆算したkとCowper及びBankのkを比較†
1種材料†
- b=1cm,h=2cm b=0.1mm,h=0.2mm刻み
- ell=10cm
- 赤:逆算したk 緑:Cowperのk
- 縦軸:k 横軸:左右の板厚(mm)

2種材料†
E同じでGの比率変える†
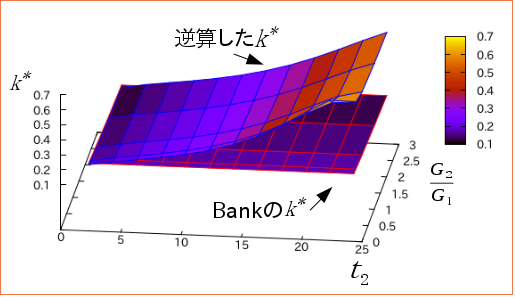
G同じでEの比率変える†
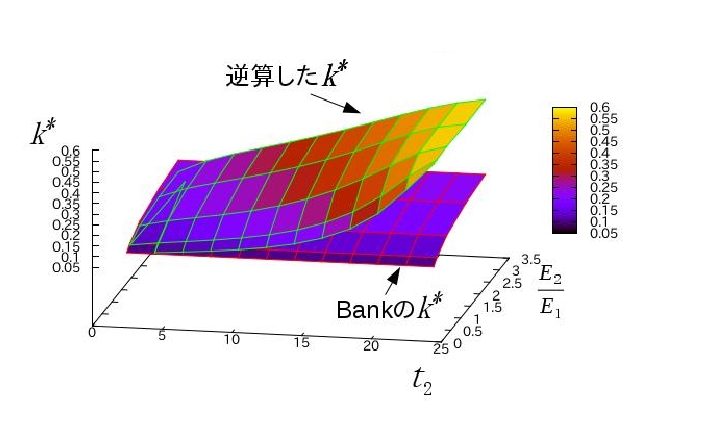
木材を厚くする†
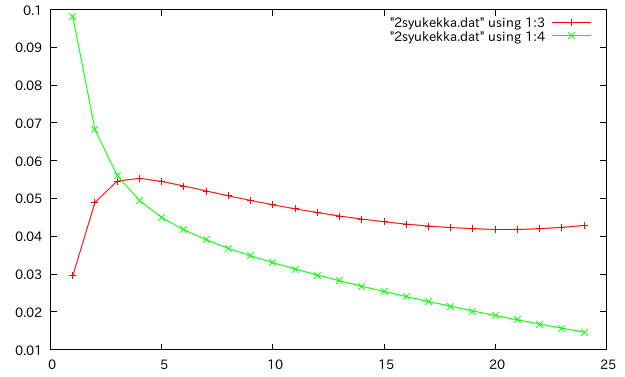
鋼材を厚くする†
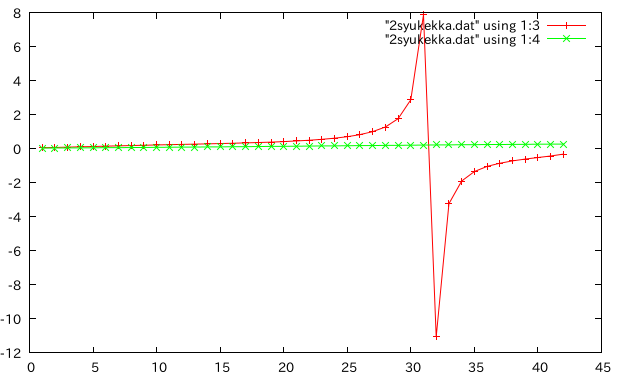
- 拡大
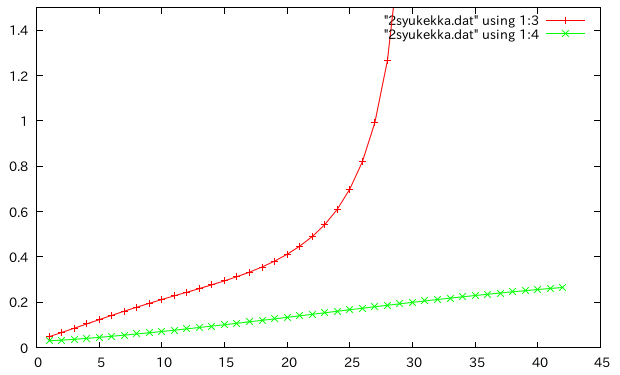
両方厚くする†
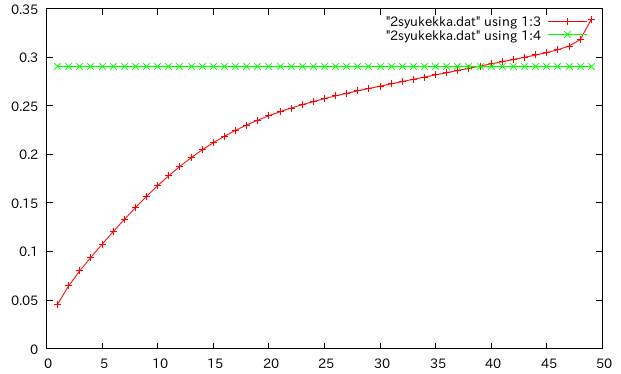
1種材料に直した時のBankのk†
k=\( \frac{10(1+\nu)(1+3m)^2}{(12+72m+150m^2+90m^3)+\nu(11+73.5m+157.5m^2+90m^3)+10n^2((3+1.75\nu)m+(3+2.25\nu)m^2)} \)
- Cowperの式とかなり似てる(計算が間違っていなければ)

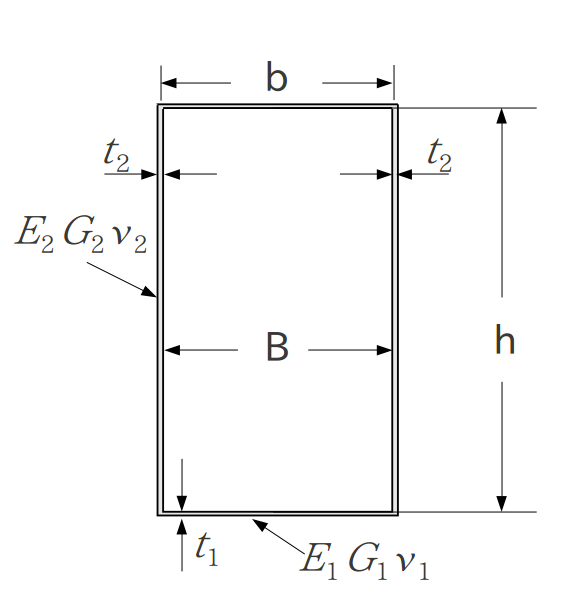
Bankのk(Shear Coefficients for Thin-Walled Composite Beams)†
m=\( \frac{bt_1}{ht_2} \)
n=\( \frac{b}{h} \)
\( \alpha \)=\( \frac{E_2}{E_1} \)
- 2種材料(\( kGA \)を\( k^{*}EA \)に換えて使う)
\( k^{*} \)=\( \frac{20(\alpha+3m)^2}{\frac{E_1}{G_1}(60m^2n^2+60\alpha mn^2)+\frac{E_1}{G_2}(180m^3+300\alpha m^2+144\alpha^2 m+24\alpha^3)+\nu_1(-30m^2n^2-50\alpha mn^2)+\nu_2(30m^2+6\alpha m-4\alpha^2)} \)
- この式を\( E1=E2,G1=G2,ν1=ν2 \)(1種材料)に直すと
\( k \)=\( \frac{20(1+3m)^2}{(180m^3+300m^2+144m+60m^2n^2+60mn^2+24)-\frac{\nu G}{E}(-30m^2+50mn^2+30m^2n^2-6m+4)} \)
- この1種材料の式をさらにb=h,t1=t2(正方形)に直すと
\( k \)=\( \frac{20}{48-3(\frac{\nu G}{E})} \)
- 逆算した\( k^* \) \( k^*=\frac{P}{EA}・\frac{\ell}{v-\frac{P\ell^{3}}{3EI}} \)
箱断面の厚さを変えてたわみの相対誤差(FEMとティモシェンコ梁理論値)を比較†
- どのくらいの板厚までCowper及びBankのkは適用できるのか。
1種材料(Cowperのk)†
- b=1cm,h=2cm b=0.1mm,h=0.2mm刻みで相対誤差を比較
- 緑:ティモシェンコ梁 赤:初等梁
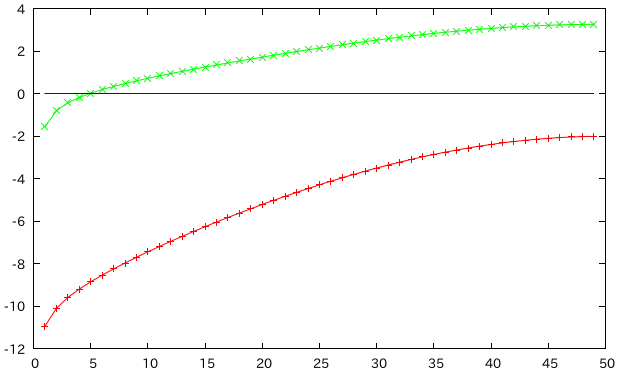
- 板厚が厚くなっても誤差はそう増えない。分厚くてもCowperのkは使える?
2種材料(Bankのk)†
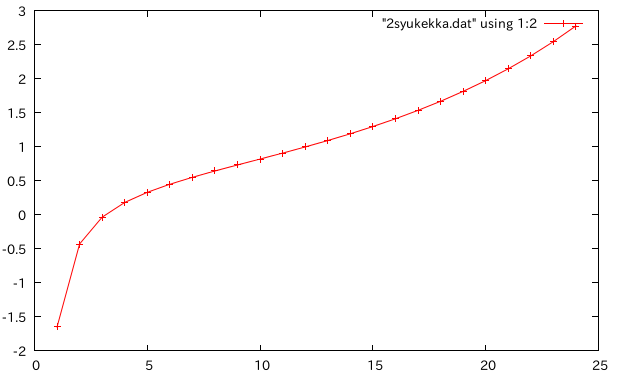
木材を厚くする†
- オンサイト木橋の箱1つ分の断面で検証,ell=10m
- 木材を鋼材とほぼ同じ(1cm)板厚にし、穴がつぶれる直前まで厚くする。鋼材の板厚は一定。
- 縦軸:相対誤差 横軸:木材の板厚
鋼材を厚くする†
- オンサイト木橋の箱1つ分の断面で検証,ell=10m
- 鋼材の厚さを1cmとし、穴がつぶれる直前まで厚くする。木材の板厚は一定。
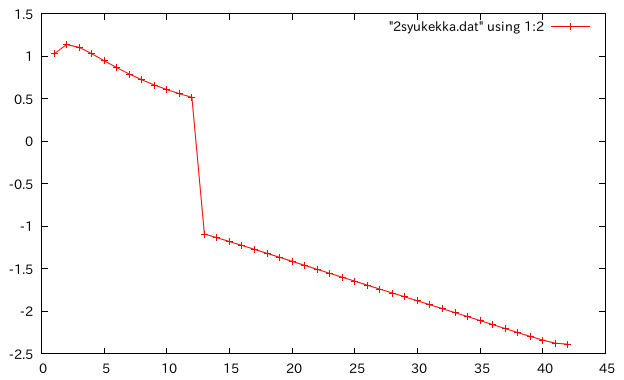
- 相対誤差(縦軸)=理論値(ティモシェンコ)-FEM/理論値(ティモシェンコ)
- 板厚が13cmになったとき、理論値よりFEMのたわみのほうが大きくなった。
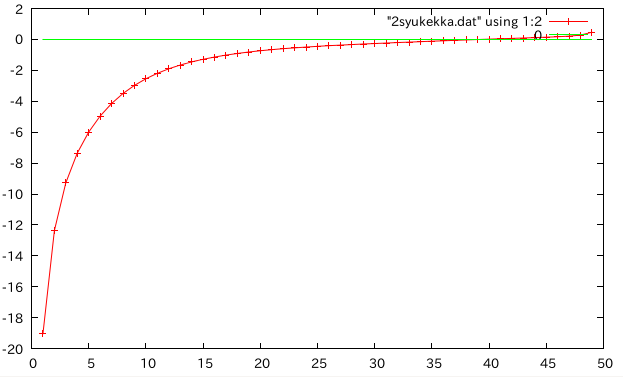
両方厚くする†
- ell=10cm b=1cm h=2cm 0.1mm,0.2mmずつ厚く
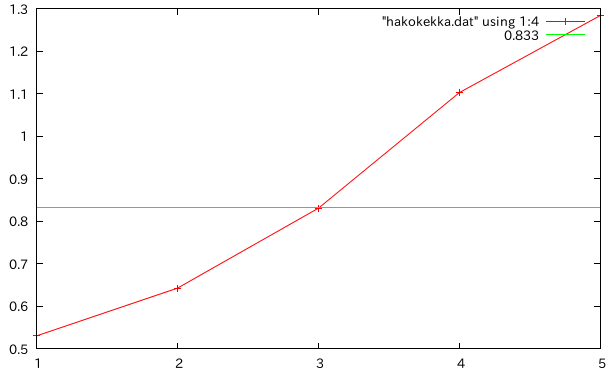
箱断面の厚さを変えてkを比較†
- b=1cm h=2cm 上下2mmずつ左右1mmずつ厚く。1=上下2mm左右1mm 5=矩形断面
- ell=10cm
- b=h=2cm
- 1=板厚1mm,1mmずつ厚くしていき、10=矩形断面
- ell=12cm
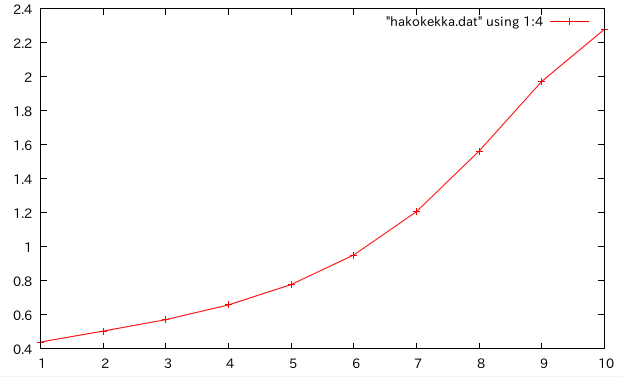
- ell=20cm
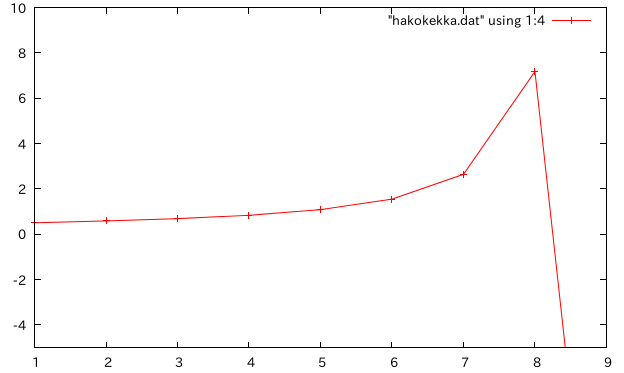
- せん断変形が小さくなるほどkが正確に推定できなくなっている
箱断面の高さを変えてkを比較†
- 理論値 cowperの長方形断面のk(肉厚間距離)

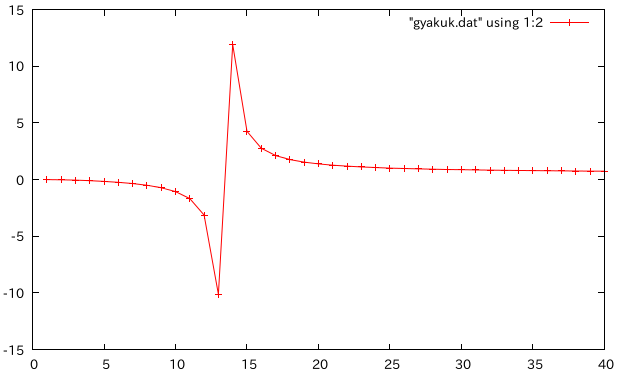
- 拡大図
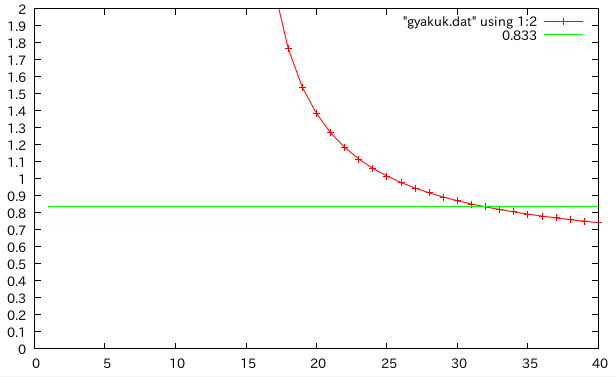
cowperによる2種類の箱断面のkを比較†
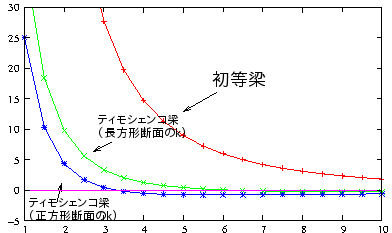
たわみの収束性†
| z分割数 | たわみ[m] |
| 100 | 9.65573E-04 |
| 200 | 9.68784E-04 |
| 300 | 9.69394E-04 |
| 400 | 9.69609E-04 |
| 500 | 9.69709E-04 |
| 600 | 9.69763E-04 |
| 700 | 9.69796E-04 |
| 800 | 9.69818E-04 |
| 900 | 9.69832E-04 |
| 1000 | 9.69843E-04 |
| 1500 | 9.69867E-04 |
| 1600 | |
| 1700 | |
| 1800 | |
| 1900 | |
| 2000 | 9.69876E-04 |
単純梁における荷重とたわみから逆算されるk†
- E=200GPa
- ν=0.333
- 等方性材料
- b=2cm
- h=2cm
- 荷重=1000N
| 長さ(mm) | たわみ(mm) | せん断補正係数k |
| 20 | 0.00175793 | 0.87936884 |
| 80 | 0.0670591 | 0.87149912 |
| 120 | 0.216744 | 5.3749995 |
| 160 | 0.507532 | -1.1933688 |
| 200 | 0.985706 | -0.46627864 |
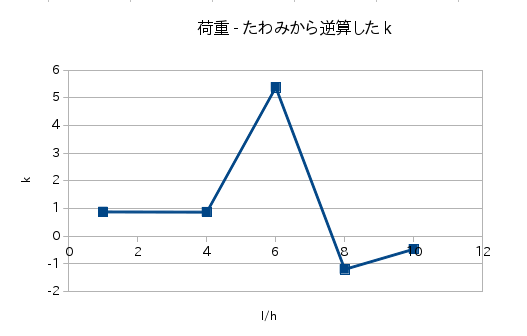
- 120のところだけkが大きくなっているのはおかしい。試しに理論値でkを導出したところそれっぽい値(0.85284829)になったため、FEMに誤差があったのかもしれない。(メッシュの分割数とか揃えてないし)
単純梁におけるFEMとティモシェンコ梁のたわみの比較(直交異方性材料)†
Asterでの異方性の設定†
MA=DEFI_MATERIAU(ELAS_ORTH=_F(E_L=,
E_T=,
E_N=,
G_LT=,
G_TN=,
G_LN=,
NU_LT=,
NU_TN=,
NU_LN=,),);
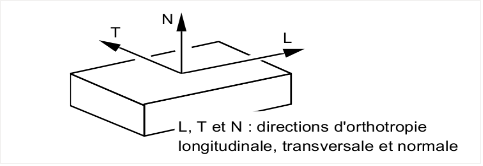 これに所定の値を入れる。(E=ヤング率,G=せん断弾性係数,NU=ポアソン比)
これに所定の値を入れる。(E=ヤング率,G=せん断弾性係数,NU=ポアソン比)
- モデルの一番長い方向が自動的にLになっている?
- たわみはE_T,G_TNに依存?
- Marc/Mentatメモ
[確認]
x=10 Y=1 Z=100の直方体要素をZ軸方向に引っ張る。
mentatにn12=0.016 n23=0.016 n31=0.4 Ex=0.28GPa Ey=0.28GPa Ez=7Gpa と入力し、
解析後のそれぞれの軸方向の変化量からポアソン比を手計算により求めたところ、
nzy=約0.4 nzx=約0.4 となった。直交異方性材料のポアソン比の関係から、
25n13=n31 n32=25n23 という関係が成り立つのでmentatに入力した値は正しいと言えるのではないか。なおn12とnxy or nyxについては不明。
ポアソン比の入れ方を変えて直交異方性を解く†
- ヤング率、せん断弾性係数の入れ方は
MA=DEFI_MATERIAU(ELAS_ORTH=_F(E_L=10000.0,
E_T=500.0,
E_N=1000.0,
G_LT=600.0,
G_TN=30.0,
G_LN=700.0,
- FEM(上三角) 33.7933mm
NU_LT=0.025,
NU_TN=0.2,
NU_LN=0.03,),);
- FEM(下三角) 33.5687mm
NU_LT=0.5,
NU_TN=0.4,
NU_LN=0.3,),);
直交異方性の設定で等方性材料を解く†
| 長さ(mm) | FEM(mm) | Timo(mm) | 誤差(mm) | 相対誤差(%) |
| 80 | 0.0670601 | 6.71325997E-02 | 7.25015998E-05 | 0.10799760 |
ちゃんと解けている。
手計算の方法†
- \( k=\frac{5}{6} \),もしくは \( k_{EG}=\frac{10E_z}{11E_z +2G_{yz}} \)
- Gについては、木材の曲げ面内のせん断に対するせん断弾性係数を用いる。(つまり\( G_{yz} \))
- ヤング率は軸方向(\( E_z \))
長さを変える†
単純梁におけるFEMとティモシェンコ梁のたわみの比較(等方性材料)†
長さを変える†
code aster†
- E=200GPa
- ν=0.499(0.5だとCode-Asterでエラーが出るため)
- G=66.711GPa(等方性材料)
- b=2cm
- h=2cm
- kはCowperの式を用いる
- 荷重=1000N
| 長さ(mm) | FEM(mm) | Timo(mm) | 誤差(mm) | 相対誤差(%) |
| 80 | 0.0550531 | 0.0674980 | 0.0124449 | 18.437 |
| 120 | 0.163147 | 0.2212467 | 0.0580997 | 26.260 |
- そもそもの誤差が大きすぎて比較にならなそう。
- E=200GPa
- ν=0.333
- 等方性材料
- b=2cm
- h=2cm
- kはCowperの式を用いる
- 荷重=1000N
| 長さ(mm) | FEM(mm) | Timo(mm) | 誤差(mm) | 相対誤差(%) |
| 20 | 0.00175793 | 1.78315002E-03 | 2.52199825E-05 | 1.4143500 |
| 80 | 0.0670591 | 6.71260059E-02 | 6.69062138E-05 | 9.96725708E-02 |
| 120 | 0.216744 | 0.22068900 | 3.94499302E-03 | 1.7875803 |
| 160 | 0.507532 | 0.51826525 | 1.07332468E-02 | 2.0709949 |
| 200 | 0.985706 | 1.0078315 | 2.21254826E-02 | 2.1953554 |
ポアソン比を変える†
- E=200GPa
- ν=0.333
- 等方性材料
- b=2cm
- h=2cm
- kはCowperの式を用いるを変える
| ポアソン比 | FEM(mm) | Timo(mm) | 誤差(mm) | 相対誤差(%)[誤差/timo] |
| 0.499 | 0.0550531 | 6.74978048E-02 | 1.24447048E-02 | 18.437199 |
| 0.49 | 0.0636544 | 6.74780011E-02 | 3.82360071E-03 | 5.6664405 |
| 0.45 | 0.0656105 | 6.73900023E-02 | 1.77950412E-03 | 2.6406054 |
| 0.40 | 0.0663956 | 6.72800019E-02 | 8.84398818E-04 | 1.3145047 |
| 0.33 | 0.0670827 | 6.71260059E-02 | 4.33027744E-05 | 6.45096824E-02 |
| 0.20 | 0.0677560 | 6.68400005E-02 | -9.15996730E-04 | -1.3704320 |
メッシュの種類を変える†
salome-mecaに入っているメッシュはNetgen(Univ形式ファイルを直接生成)とGmsh(Gmsh形式を直接生成)があるらしい。
- E=200GPa
- ν=0.333
- 等方性材料
- b=2cm
- h=2cm
- kはCowperの式を用いる
- Nodes 47908
- voliumes 211673
- Gmsh
- Netgen3D 0.507532
- Tetrahedron(Netgen) 0.507532
分割数を変える†
glmageReader+resseract-ocr-jpnのインストール†
- なお、日本語の文章を読み取る場合はUbuntuソフトウェアセンターの検索欄からtesseract-ocr-jpnを探し、インストール
- glmageReaderを起動し、File→Configure→Configuration→Priferred language→日本語を選択
- Languages→日本語を選択→適用
- を行うと日本語の文章も読み取れるっぽい(未確認)
6/22までの課題†
- ヤング率:2840MPa
- ポアソン比:0.313
- 荷重:1000N
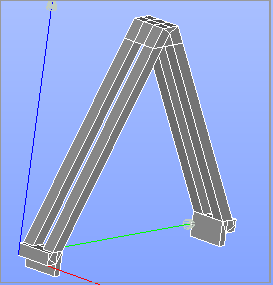
| 拘束条件 | 載荷条件 | 要素の種類 | 要素数 | 節点数 | たわみ(mm) | 体積(mm\( ^3 \)) |
| 線 | 線 | 4面体2次 | 80404 | 21967 | 0.73 | 11956.7 |
Salome-Mecaメモ†
Salome-Mecaの単位†
| 長さ | m | cm | mm |
| 応力 | Pa | 10\( ^4 \)Pa | MPa |
code-asterコマンドリスト†
http://opencae.gifu-nct.ac.jp/pukiwiki/index.php?plugin=attach&refer=SALOME-Meca%A4%CE%BB%C8%CD%D1%CB%A1%B2%F2%C0%E2&openfile=00-00.pdf
- 3.設定→荷重の設定 FOACEは間違い 正しくは○FORCE
Code-Asterにおけるエラー†
- 線載荷のとき以下を残したままにする
- MAIL=MODI_MAILLAGE(reuse=MAIL,MAILLAGE=MAIL,ORIE_PEAU_3D=_F(GROUP_MA=('Group_xxx',),),);
- ポアソン比を0.5にする(0.499とかだとエラーは出ない)
- 2cm角の片持ち梁の長さを12cmから16cmにしたところ、エラー
- longueur=長さ
- メッシュを粗くしたらエラーはでなかったので、要素数,節点数が原因と見られる。
- Nodes 76944
- Volumes 379773 でエラー
- Nodes 42779
- Volumes 193780
- とりあえずこの数値まではうまくいっているので、(要素数=メッシュ長さの三乗に比例)することを考慮してこの値を超えないように解析していこう。

- グループ(saikaとかkotei)を作らないでAsterしたときのエラー
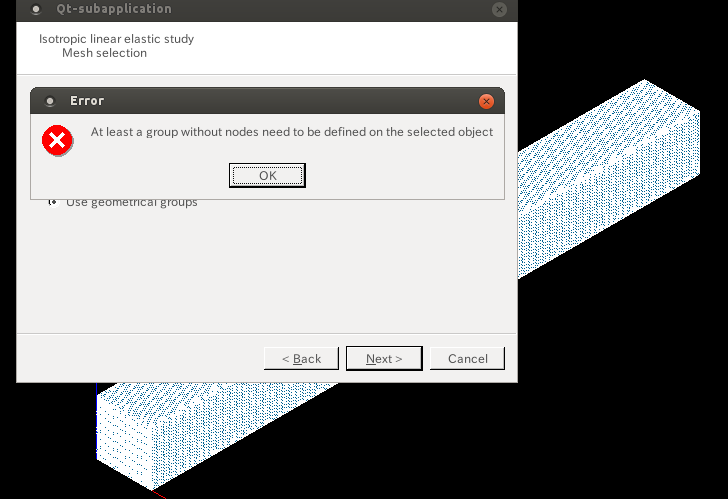
Fortranメモ†
計算ツール†
- ティモシェンコ梁のたわみ(片持ち梁) \( v=\frac{P\ell^{3}}{3EI}+\frac{P\ell}{kGA} \)
- \( k \)について解くと \( k=\frac{P}{GA}・\frac{\ell}{v-\frac{P\ell^{3}}{3EI}} \)
- 等方性材料のせん断弾性係数 \( \frac{E}{2(1+ν)} \)
- せん断補正係数k
- せん断が断面に一様にかかるとK=1
- 各断面ごとに数値が変わる
- 矩形断面の場合
- timoshenko \( \frac{2}{3} \)
- Cowper \( k=\frac{10(1+ν)}{12+11ν} \) (ν=0で\( \frac{5}{6} \))
- せん断弾性係数G
- 剛性率の一つ、せん断力による変形のしにくさに関係する物性値
- 部材によって変わる
- 箱断面のk
m=\( \frac{bt_1}{ht} \)
n=\( \frac{b}{h} \)
k=\( \frac{10(1+\nu)(1+3m)^2}{(12+72m+150m^2+90m^3)+\nu(11+66m+135m^2+90m^3)+10n^2((3+\nu)m+3m^2)} \)
- 正方形箱断面のk
\( k=\frac{20(1+ν)}{48+39ν} \)
wikiの使い方†
libre officeの使い方†
- Calcでグラフを作る
- 表を作って範囲を選択,グラフ,散布図,データ系列でx軸y軸の範囲を選択,グラフ要素でタイトル等を入力
プログラム†
8/28 3Dモデルを作る†
- implicit none 変数を作るために宣言文を使用しなければならない。面倒くさくはなるが、ここで宣言した変数以外は使用できないため、失敗を早い段階で発見できる。また、宣言文を見れば今どんな変数を利用しているか分かる。
- 実数型(2.345とか)→real
- 整数型(1,-3,0とか)→integer
- implicit real*8(a-h,o-z) a-h,o-zで始まる変数は実数型となり、i-nで始まる変数は整数型となる。手間は省けるが予期せぬエラーが出やすい。
- d0 10の0乗(つまり1)、d3 10の3乗
- nx,ny,nz 要素分割数
- xn,yn,zn 要素1つあたりの長さ(座標を入れるのに必要)
- nset 節点番号
- x(nset),y(nset),z(nset) 座標
- doループ
- do k=0,nz
- z(nset)=k*zn
- end do
0からnzまでz(nset)=k*znを繰り返す
- (
do k=0,nz!z
do j=0,ny!
do i=0,nx!x方向分割数を担当
nset=1+i+j*(nx+1)+k**1
x(nset)=i*xn
y(nset)=j*yn
z(nset)=k*zn
end do
end do
end do
- )
- doループはiを一通り終えてからj,kと進む。
- 1列目は1+iで節点番号が決まっていく。
- 1列目を終えるとiが0に戻り、jが1となる。するとj*(nx+1)に1足してのスタートとなるため、1段上へ上がる。
- xy面を終えるとi,jが0に戻り、kが1となる。するとk**2[x方向の節点数*y方向の節点数]に1足してのスタートをなるため、z方向に一つ進む。
※節点数は分割数+1なので、nx+1,ny+1
- print
- (
print'(i6,a,f9.6,a,f9.6,a,f9.6)',&
&i,',',x(i),',',y(i),',',z(i)
- )
- i6 integer,つまり整数型の入れ物を6個つくる
- a 下の段のコンマと対応。,がプリントされる
- f9.6 9個あって小数点以下が6個
※&でつなぐと改行しても同じ行にいることになる。
- (
nyou=0
do k=0,nz-1
do j=0,ny-1
do i=1,nx
nyou=nyou+1
mesh(nyou,1)=i+j*(nx+1)+k**3
mesh(nyou,2)=mesh(nyou,1)+(nx+1)
mesh(nyou,3)=mesh(nyou,2)+(nx+1)*(ny+1)
mesh(nyou,4)=mesh(nyou,1)+(nx+1)*(ny+1)
mesh(nyou,5)=mesh(nyou,1)+1
mesh(nyou,6)=mesh(nyou,5)+nx+1
mesh(nyou,7)=mesh(nyou,6)+(nx+1)*(ny+1)
mesh(nyou,8)=mesh(nyou,5)+(nx+1)*(ny+1)
end do
end do
end do
- )
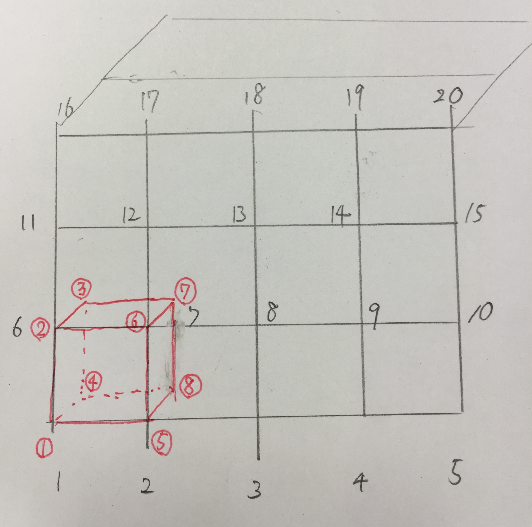
- 節点番号 1,2,3,4... 要素番号 mesh(nyou, ) ①,②,③...
- mesh(nyou,1)=i+j*(nx+1)+k**4 ①は1,2,3,4,5,6...と進んでいく
- mesh(nyou,2)=mesh(nyou,1)+(nx+1) ②は①の(nx+1)つまり一行上を進んでいく
- mesh(nyou,3)=mesh(nyou,2)+(nx+1)*(ny+1) ③は②のz方向奥に進んでいく
的な
- コンパイル,cgx
- gfortran xxx.f90 -o xxx
- ./kukei >kukei.inp
- cgx_2.5 -c xxx.inp
- cutでメッシュ分割を見れる。
8/29 nz(要素分割数)を別々に指定、梁を解く†
- Calculix 有限要素法のフリーのソフトウェア。商用ソフトABAQUSと同様の入力書式をもつ。
- ソルバー 計算を実行するソフトウェア。(ccx,code-asterなど)
- ポストプロセッサー ソルバーで計算した結果を表示するためのソフトウェア。計算結果を3Dモデル上で表示したり、アニメーションで見せたり、グラフを作成したり、様々な方法で結果を参照できる。(cgx,salomeのpost-pro)
- プリプロセッサー ソルバに必要な入力データを作成するためのソフトウェア。メッシュを作成したり、境界条件や荷重を設定したりして解析モデルを作り、ソルバに渡すためのインプットファイルを出力する。(salomeのgeometry,mesh)
- nzを別々に指定
- ellをell1,ell2,ell3等と分け、ellall=ell1+ell2+ell3等とおく。よって要素一つあたりの長さもzn1=ell1/nz1,zn2=ell2/nz2,zn3=ell3/nz3となる。
- 節点番号を決めるdoループも3個作る。
- (
do k=0,nz1-1!z
do j=0,ny!
do i=0,nx!x方向分割数を担当
nset=1+i+j*(nx+1)+k**5
x(nset)=i*xn
y(nset)=j*yn
z(nset)=k*zn1
end do
end do
end do
nset1=nset
- )
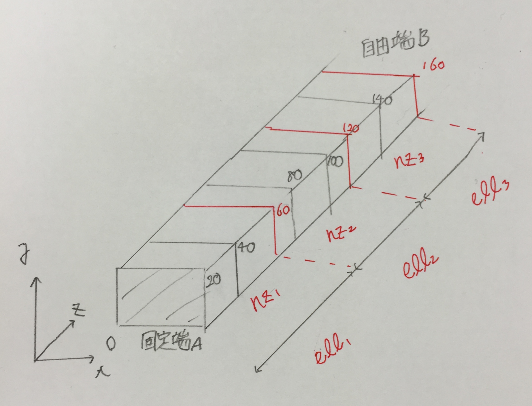
- nz1の領域では40まで節点番号をつけ、nz1とnz2の境界にあたる41以降はnz2の領域でつける。そのためnz1-1までとする。(nz2も同様,nz3は最後までつけていいので-1は不要)
- nset1=nset(節点番号)とおき、次のdoループでnset=nset1+1+i+j*(nx+1)+k**6とすることで前回の続きの節点番号から始めることができる。
- 要素番号はdoループを k=0,nz1+nz2+nz3-1までとすればそのままのプログラムで良い。
- 解析 cardといわれるオプションをinpファイルに入れることで様々な解析ができる。
- 解析の流れ
- コンパイルし、中身をinpファイルに出力。
- ccx_2.5 xxx(ccxで計算, .inpは省略して良い)
- cgx_2.5 xxx.frd(cgxで動きや応力を見る。)
- vi xxx.dat(生のファイルを見る)
- たわみの平均を出すプログラム(tawahei.f90)に入り、行数,入力,出力などを確認してコンパイル。
- (
!境界条件
print'("*BOUNDARY")'
print'("kotei,1,3")'
- )
1=x,2=y,3=zという意味。1,3は1~3すべて固定ということ。
- (
!載荷点の節点群を書きだす
print'("*NSET,NSET=saika")'
do i=1,nitimen
nsaika=nitimen*nz+i
print'(i6,a)',nsaika
end do
- )
nitimen=(nx+1)*(ny+1) つまりnitimenにnz(分割数)をかけ、その次からスタートすることで載荷点の節点群を書き出すことができる。(nz方向の節点数も分割数+1だから)
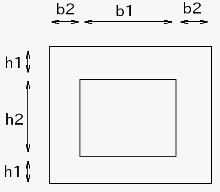
8/31 L断面or箱断面†
- 例えばL断面はx方向の長さが途中から変化するため、1段ごとの節点番号の増分が途中から変化する。そのため要素は分けて考えなければならない。(箱断面も同様)
- (
!ヤング率
ezz=7.694d3
exx=ezz/25.0d0!x軸方向のヤング率
eyy=ezz/25.0d0!y軸方向のヤング率
ezz2=206.0d3!z軸方向のヤング率
!ポアソン比の入力
poixy=0.016d0
poixz=poixy
poiyx=poixy
poiyz=poixy
poizx=0.4d0
!せん断弾性係数の入力
gxy=ezz/15.0d0
gxz=gxy
gyz=gxy
- )
このへんは異方性のカードを挿し込まなければ働かない部分。現段階では働いてないので無視してよい。等方性で解く場合はカードのヤング率、ポアソン比を変える。
- 境目の要素の包み方(y方向)
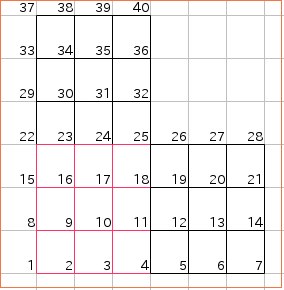 赤で囲まれた部分の要素を包む際、15~17まででやめて、上部分で要素を包むとき22から始めようとすると増分が変わってうまくプログラムできない。
そのためy(上)方向に関しては22~24まで要素を包んでしまった方が良い。
赤で囲まれた部分の要素を包む際、15~17まででやめて、上部分で要素を包むとき22から始めようとすると増分が変わってうまくプログラムできない。
そのためy(上)方向に関しては22~24まで要素を包んでしまった方が良い。
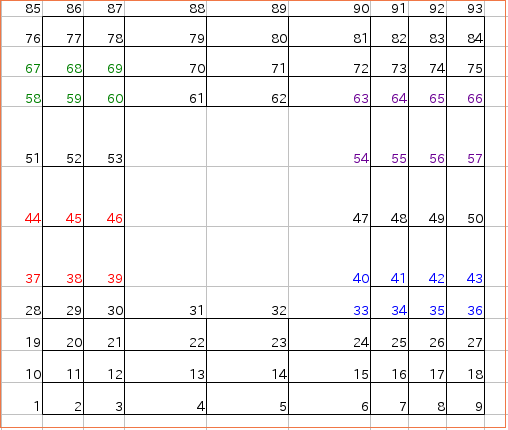
- 箱断面は増分が変わる場所が多い(しかも左右ずれている)ことに注意
9/8 スパンを自動で変えてたわみを計算†
- スパンを自動で変えてたわみを計算させるプログラム(片持ち梁)
- 単位はすべてm,MN
- スパンは[ell=ell+0.1d0]で決めることに注意
- (
プログラムをコンパイル
jobという白色のファイルが出てくるので
chmod 744 job
と入れると緑色になる
./jobで実行するとdatファイルが出てくる。
- )
9/17 実行ファイル†
- (ファイル名.sh)の中に実行させたいコマンドとかを書く。
- chmod 755 (ファイル名.sh) で実行ファイルに変える。
9/30 ファイル入出力†
10/1 自動計算†
10/30 プログラムの改良†
11/1 改良,過去のもの†
11/11 もらいもの、改良†
12/17 修正†
12/19 改良†
1/13 後藤さんによる改良†
tex†
まず始めに†
参考になるページ†
使い方†
- viでtexファイルを編集
- platex (ファイル名)でコンパイル。
- pxdvi (ファイル名)で編集されたものを見る。
- 確認しながら編集
- :w 保存
- :!platex aaa.tex コンパイル
- :!pxdvi aaa& 画面クリックで更新
- 空白を入れたい場合は全角の空白を入れること
- ※全角と半角では意味が違う
画像をepsファイルに変換†
一個ずつ†
- convert test.png test.eps
- for infile in *.png; do
- convert \( infile \){infile%.*}.eps ;
- done
gnuplot†
参考になるページ†
3Dグラフ†
使い方†
プロットする†
- ターミナルで gnuplot と打つ
- plot '(ファイル名)'でプロットされる。
複数のデータをプロット†
- gnuplot> plot "output1.dat" using 1:2 w lp
- gnuplot> replot "output1.dat" using 1:3 w lp
軸に平行な線†
右上の式を消す†
表示する範囲を決める。†
- gnuplot> set xr[0:6.28]
- gnuplot> set yr[-1.5:1.5]
軸の目盛りを変える†
- gnuplot> set xtics 1
- gnuplot> set ytics 1.5
- これでx軸は1ごと、y軸は1.5ごとになる。
Xfig†
参考になるページ†
Calculix†
マニュアル†
- ホームの一つ前に戻る
- opt
- Calculix
- ccx_2.5.pdf
後藤資料内メモ†
http://www.str.ce.akita-u.ac.jp/cgi-bin/gwiki/wiki.cgi?CalculiX%a5%e1%a5%e2
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)

 これに所定の値を入れる。(E=ヤング率,G=せん断弾性係数,NU=ポアソン比)
これに所定の値を入れる。(E=ヤング率,G=せん断弾性係数,NU=ポアソン比)

 赤で囲まれた部分の要素を包む際、15~17まででやめて、上部分で要素を包むとき22から始めようとすると増分が変わってうまくプログラムできない。
そのためy(上)方向に関しては22~24まで要素を包んでしまった方が良い。
赤で囲まれた部分の要素を包む際、15~17まででやめて、上部分で要素を包むとき22から始めようとすると増分が変わってうまくプログラムできない。
そのためy(上)方向に関しては22~24まで要素を包んでしまった方が良い。