卒論日誌†
| 日付 | 時間帯 | 作業時間(hr) | 内容 | 立会 |
| 4/12 | 15:30-16:30 | 1 | タイピング | |
| 4/13 | 14:30-16:30 | 2 | タイピング | |
| 4/20 | 15:30-16:30 | 1 | vi | |
| 4/21 | 13:30-16:30 | 3 | vi | |
| 4/23 | 13:00-16:30 | 3.5 | vi | |
| 4/25 | 11:00-14:00 | 3 | fortran | |
| 4/28 | 11:30-14:00 | 2.5 | fortran | |
| 4月合計 | | 16 | | |
| 5/10 | 15:00-19:00 | 4 | salome | |
| 5/13 | 11:00-12:00 | 1 | salome | |
| 5/14 | 11:00-12:00 | 3 | salome | |
| 5/21 | 14:00-17:00 | 3 | salome | |
| 5/22 | 15:00-16:30 | 1.5 | salome | 近藤さん |
| 5/24 | 14:00-22:00 | 8 | salome | 近藤さん |
| 5/27 | 12:30-18:30 | 6 | 現場見学 | 後藤さん・野田さん |
| 5月合計 | | 26.5 | | |
| 合計 | | 42.5 | | |
| 6/4 | 12:30-14:30 | 2 | gnuplot | 近藤さん |
| 6/8 | 16:30-18:30 | 2 | gnuplot | |
| 6/9 | 15:30-17:00 | 1.5 | gnuplot | |
| 6/13 | 16:00-18:30 | 2.5 | gnuplot | |
| 6/20 | 15:30-17:30 | 2 | salome | |
| 6/21 | 12:30-17:30 | 5 | salome | 近藤さん |
| 6/22 | 10:30-12:30 | 2 | salome | |
| 6/22 | 20:00-23:00 | 3 | gnuplot | |
| 6/23 | 12:30-14:00 | 1.5 | salome | |
| 6/28 | 11:30-16:00 | 4.5 | salome | |
| 6/30 | 16:30-19 | 2.5 | salome | |
| 6月合計 | | 28.5 | | |
| 合計 | | 71 | | |
| 7/2 | 16:30-18:00 | 1.5 | salome | |
| 7/3 | 15:00-16:00 | 1 | salome | |
| 7/5 | 16:00-17:00 | 1 | salome | |
| 7/9 | 16:00-19:00 | 3 | salome | |
| 7/15 | 16:00-18:00 | 2 | salome | |
| 7/24 | 13:00-16:00 | 3 | salome | |
| 7/30 | 14:00-18:00 | 4 | salome | |
| 7/31 | 14:00-16:00 | 2 | salome | |
| 7月合計 | | 17.5 | | |
| 合計 | | 88.5 | | |
| 8/1 | 12:00-17:00 | 5 | salome | |
| 8/3 | 16:00-17:00 | 1 | salome | |
| 8/5 | 12:00-16:00 | 4 | salome | |
| 8/20 | 12:00-17:00 | 5 | salome | |
| 8/24 | 13:30-14:30 | 1 | salome | |
| 8/25 | 11:30-14:30 | 3 | salome | |
| 8/29 | 13:00-15:30 | 2.5 | salome | |
| 8/31 | 11:30-17:30 | 6 | salome | |
| 8月合計 | | 27.5 | | |
| 合計 | | 116 | | |
| 9/1 | 12:00-17:00 | 5 | salome | |
| 9/5 | 12:00-18:30 | 6.5 | 現場見学 | 後藤さん・野田さん |
| 9/7 | 15:00-17:00 | 2 | salome | |
| 9/9 | 16:00-17:00 | 1 | salome | |
| 9/10 | 13:00-17:00 | 4 | salome | |
| 9/13 | 14:00-16:00 | 2 | salome | |
| 9/23 | 16:00-18:30 | 2.5 | salome | |
| 9/24 | 13:00-15:30 | 2.5 | salome | 近藤さん |
| 9/25 | 15:00-18:00 | 3 | salome | 近藤さん |
| 9/26 | 13:00-17:00 | 4 | salome | 近藤さん |
| 9/27 | 13:00-16:30 | 3.5 | 発表資料作成 | |
| 9/27 | 21:00-23:00 | 2 | 発表資料作成 | |
| 9/28 | 3:00-5:00 | 2 | 発表資料作成 | |
| 9/28 | 14:00-17:00 | 3 | 発表資料作成 | |
| 9/28 | 20:00-23:00 | 3 | 発表資料作成 | |
| 9/29 | 2:00-5:00 | 3 | 発表資料作成 | |
| 9/29 | 11:00-16:00 | 5 | 発表資料作成 | |
| 9/29 | 19:00-22:00 | 3 | 発表資料作成 | |
| 9月合計 | | 57 | | |
| 合計 | | 173 | | |
| 10/3 | 12:00-16:00 | 4 | salome | |
| 10/6 | 16:00-17:00 | 1 | salome | |
| 10/7 | 9:30-12:00 | 2.5 | salome | |
| 10/9 | 13:00-17:00 | 4 | salome | |
| 10/11 | 18:30-19:30 | 1 | salome | |
| 10/12 | 15:00-16:00 | 1 | salome | |
| 10/14 | 11:00-16:30 | 5.5 | salome | |
| 10/18 | 14:00-16:00 | 2 | salome | |
| 10/19 | 16:00-17:00 | 1 | salome | |
| 10/21 | 10:30-12:00 | 1.5 | salome | |
| 10/26 | 15:00-17:30 | 2.5 | salome | |
| 10/27 | 16:00-18:00 | 2 | salome | |
| 10月合計 | | 28 | | |
| 合計 | | 201 | | |
| 11/2 | 17:00-19:00 | 2 | salome | |
| 11/3 | 15:00-17:00 | 2 | salome | |
| 11/4 | 11:00-12:00 | 1 | salome | |
| 11/7 | 11:00-15:00 | 4 | salome | |
| 11/10 | 16:00-18:00 | 2 | salome | |
| 11/11 | 11:00-15:00 | 4 | salome | |
| 11/17 | 16:00-19:00 | 3 | salome | |
| 11/18 | 11:00-12:30 | 1.5 | salome | |
| 11/24 | 17:00-18:30 | 1.5 | salome | 近藤さん |
| 11/25 | 10:30-17:00 | 6.5 | salome | |
| 11/29 | 16:00-19:00 | 3 | salome | 近藤さん |
| 11/30 | 16:30-20:30 | 4 | salome | 近藤さん |
| 11月合計 | | 34.5 | | |
| 合計 | | 235.5 | | |
| 12/1 | 14:00-18:00 | 4 | salome | 近藤さん |
| 12/2 | 11:00-16:00 | 5 | salome | |
| 12/4 | 15:00-18:00 | 3 | salome | |
| 12/5 | 16:00-17:00 | 1 | salome | |
| 12/6 | 19:00-22:30 | 3.5 | salome | |
| 12/7 | 14:30-20:00 | 5.5 | salome | 近藤さん |
| 12/10 | 14:30-17:30 | 3 | salome | |
| 12/13 | 17:00-19:00 | 2 | salome | |
| 12/14 | 12:00-17:00 | 5 | salome | |
| 12/15 | 17:00-18:00 | 1 | salome | |
| 12/16 | 20:00-1:00 | 5 | 発表資料作成 | |
| 12/17 | 15:00-22:00 | 7 | 発表資料作成 | |
| 12/18 | 15:00-21:00 | 6 | 発表資料作成 | |
| 12/19 | 19:00-4:00 | 9 | 発表資料作成 | |
| 12月合計 | | 60 | | |
| 合計 | | 295.5 | | |
| 1/10 | 15:00-22:30 | 7.5 | salome | |
| 1/11 | 14:30-17:00 | 2.5 | salome | |
| 1/13 | 12:00-13:00 | 1 | salome | |
| 1/16 | 14:30-18:00 | 3.5 | salome | 近藤さん |
| 1/18 | 14:00-17:00 | 3 | salome | |
| 1/19 | 15:00-18:00 | 3 | salome | |
| 1/20 | 12:00-13:00 | 1 | salome | |
| 1/23 | 16:00-22:00 | 6 | salome | 近藤さん |
| 1/26 | 19:00-22:00 | 3 | salome | |
| 1/27 | 16:00-23:00 | 7 | salome | |
| 1/28 | 11:00-20:00 | 9 | salome | |
| 1/29 | 16:00-21:00 | 5 | salome | |
| 1月合計 | | 51.5 | | |
| 合計 | | 347 | | |
| 2/1 | 14:00-20:00 | 6 | salome | |
| 2/2 | 16:00-19:00 | 3 | salome | |
| 2/5 | 14:00-19:30 | 5.5 | salome | |
| 2/6 | 16:00-21:00 | 5 | salome | |
| 2/7 | 14:00-19:00 | 5 | 概要作成 | |
| 2/8 | 15:00-20:00 | 5 | 概要作成 | |
| 2/9 | 16:00-24:00 | 8 | 概要作成 | |
| 2/10 | 24:00-2:00 | 2 | 概要作成 | |
| 2/10 | 15:00-22:00 | 7 | 概要作成 | |
| 2/11 | 15:00-19:00 | 4 | 発表資料作成 | 近藤さん |
| 2/12 | 14:00-22:30 | 8.5 | 発表資料作成 | |
| 2/13 | 13:00-18:00 | 5 | 発表資料作成 | |
| 2/14 | 11:00-14:00 | 3 | 発表資料作成 | |
| 2月合計 | | 67 | | |
| 合計 | | 414 | | |
卒論テーマ†
載荷試験†
- 今回のFEM解析の比較対象として、山口大学で行われたCLT床版の載荷試験の結果を用いることとする。
- CLTの寸法
(X,Y,Z)=(4000,240,2000)[mm]
- 1層モデル
- 材料定数
- (
E_L=1700000000
E_T=200000000
E_N=3500000000
G_LT=333333333
G_TN=333333333
G_LN=333333333
NU_LT=0.194
NU_TN=0.0229
NU_LN=0.4
- )
- 荷重の大きさ
80kN
- 載荷面
200mm*500mmとし、中心に載荷する。
- 変位を読み取る箇所
(X,Y,Z)=(2000,240,1000)[mm]
- 境界条件
面固定・片方は全固定、もう片方はローラー
卒論メモ†
1/24†
- 層毎の異方性が逆に設定されていたので、正しい設定に直して計算してみた。
(設計図のヤング率が部分的に書かれていたので、勘違いしていた。)
| モデル | 変位 | 輪荷重載荷前 | 相対誤差 | 輪荷重載荷後 | 相対誤差 |
| 1層(一次) | 1.449mm | 1.990mm | 27.2% | 2.005mm | 27.7% |
| 1層(二次) | 1.536mm | | 22.8% | | 23.4% |
| 8層(一次) | 1.921mm | | 3.47% | | 4.19% |
| 8層(二次) | 2.063mm | | 3.67% | | 2.89% |
- 1層に関しては誤差が大きく出てしまったが、実物に近い8層の誤差は小さくなったので、とりあえず誤差の問題は解決した。
1/19†
- CLTのモデルを引き板も考慮して作成した。しかし、変位は2.468mmでした。
誤差の原因は未だに解決していません。

1/16†
- そもそも8層モデルの設定が間違っているかもしれないので、
1層モデルの条件を8層モデルの設定に入れて、値が同じになるのか試してみた。
結果は以下の通りである。
| 変位 |
| 1層モデル | 1.443mm |
| 8層モデル | 1.443mm |
- 値が同じになったので、8層モデルの設定は合っていました。なので、誤差の原因は別にあると考えられる・・・。
1/10†
- ポアソン比を見直した結果、8層モデルの値が間違っていたため、次のように訂正した。
- (
kyoujiku=DEFI_MATERIAU(ELAS_ORTH=_F(E_L=5000000000,
E_T=200000000,
E_N=200000000,
G_LT=333333333,
G_TN=333333333,
G_LN=333333333,
NU_LT=0.4,
NU_TN=0.016,
NU_LN=0.4,),);
jakujiku=DEFI_MATERIAU(ELAS_ORTH=_F(E_L=200000000,
E_T=200000000,
E_N=5000000000,
G_LT=333333333,
G_TN=333333333,
G_LN=333333333,
NU_LT=0.4,
NU_TN=0.016,
NU_LN=0.016,),);
- また、計算結果としては、8層モデルの値が2.397mmとなったが、未だに誤差は大きいままである。
12/16†
- 論文報告書を読み直したら、静的載荷試験の方法が以下のように載ってたので、計算をやり直したいと思います。
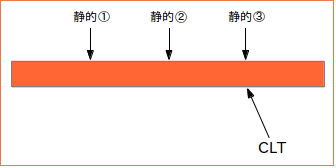
- LibreOffice関連のソフトに日本語を打っても、すべて□で表示されてしまい、作業が出来ない。
12/15†
- 近藤さんによると、藤田さんのモデルは全面拘束になっていないらしいので、拘束の範囲を藤田さんのモデルに合わせて、二次要素で解いた。
- 結果は、たわみが1.938mmとなった。
12/14†
- 12/13に用いた条件で、8層モデルを解いた結果、たわみが3.012mmとなった。
- また、同じモデルを二次要素で解いた結果、たわみが3.329mmとなった。
12/13†
- H型鋼ではなく、ゴム板の上に設置していることにして解いてみた。
- ゴム板が床版と接している面の範囲は設計図より、135mm*3360mmが二箇所とした。
- また、片方のみDZ=0とした。
- 結果は、1層モデルのたわみが1.804mmとなった。
- あと、2010mmという値はcltの寸法ではなく、支持桁間隔(cltの寸法2000mmにH型鋼とゴム板の中心から5mmずらしたものを足した値)です。
10/14†
- (
kyoujiku=DEFI_MATERIAU(ELAS_ORTH=_F(E_L=5000000000,
E_T=200000000,
E_N=200000000,
G_LT=333333333,
G_TN=333333333,
G_LN=333333333,
NU_LT=0.016,
NU_TN=0.016,
NU_LN=0.4,),);
jakujiku=DEFI_MATERIAU(ELAS_ORTH=_F(E_L=200000000,
E_T=200000000,
E_N=5000000000,
G_LT=333333333,
G_TN=333333333,
G_LN=333333333,
NU_LT=0.4,
NU_TN=0.016,
NU_LN=0.016,),);
7/9†
- とりあえず、等方性から計算の確認をする。
- また、異方性の条件を決めるL,N,Tの向きをはっきりさせる。(一番長いのがL?)
| Ezz | Exx | Eyy | Gxy | Gyz | Gzx | NUxy | NUyz | NUzx |
| 条件 | 2600Pa | 2600Pa | 2600Pa | 1000 | 1000 | 1000 | 0.3 | 0.3 | 0.3 |
| EPSIz |
| FEM | -0.000384615 |
| 手計算 | -0.000384615 |
7/3†
- 適当に決めたE,G,NUの条件下で縦の棒部材にz軸方向に面載荷し、得られたひずみと手計算のひずみが一致するのか。
| Ezz | Exx | Eyy | Gxy | Gyz | Gzx | NUxy | NUyz | NUzx |
| 条件 | 150Pa | 6Pa | 6Pa | 10 | 10 | 10 | 0.4 | 0.016 | 0.016 |
| EPSIx | EPSIy | EPSIz |
| FEM | 1.06e-4 | 6.67e-2 | -0.167 |
| 手計算 | 2.67e-3 | 2.67e-3 | -6.67e-3 |
- 全然一致しなかった・・・。
- EPSIxとEPSIyの値が異なる原因が分からない。
6/25†
- l=100mm,b=10mm,h=10mmの棒部材に以下の条件で載荷してみた。
- Ezz=7GPa,Exx=Eyy=0.28GPa,Gxy=Gyz=Gzx=466666666.7,NUxy=0.4,NUyz=NUzx=0.016,P=100N
| FEM(m) | Timo(m) | 相対誤差(%) |
| 0.00596518 | 0.00597143 | 0.105 |
近藤より(12/5)†
- 単純梁の中央に等分布荷重が載ったときの、ティモシェンコ梁理論の梁中央のたわみは、
\( v_{(a+\frac{b}{2})}=\frac{5qb^{4}}{384EI}+\frac{5qab^{3}}{48EI}+\frac{qa^{2}b^{2}}{4EI}+\frac{qa^{3}b}{6EI}+\frac{qb^{2}}{8kGA}+\frac{qab}{2kGA} \).
- ここで、諸元は
- a:梁の等分布荷重が載っていない区間
- b:梁の等分布荷重が載っている区間
- 他はいつも通りなので、省略。
- a=0を代入した感じでは、多分合っていると思いますが、確認して下さい......。
- もし、計算をどうやったのか興味がある場合は、(アプリケーション-->教育・教養-->)wxMaxmaで&link(tyu_bun.wxm,http://www.str.ce.akita-u.ac.jp/~gotouhan/j2016/kondo/clt/tyu_bun.wxm)を開いて、見て下さい。
近藤より(11/30)†
海老名君がどうやって材料定数を決めたのか判りませんが、それだと合わない気がします......。以下、参考までに。
集成材における材料定数の数値モデル化について、&link(2006年度の橋本さんの修論,http://www.str.ce.akita-u.ac.jp/~gotou/tebiki/#ron06)あたりに詳しく書かれているので、これを参考にしてみると、CLTの図面より、ひき板一枚ずつのヤング率は、
- \( E_{x}=\frac{E_{z}}{25}=0.2 \)GPa, \( E_{y}=\frac{E_{z}}{25}=0.2 \)GPa, \( E_{z}=5 \)GPa
で、それを平均化した値は、
- \( \overline{E_{x}}=1.7 \)GPa, \( E_{y}=0.2 \)GPa, \( \overline{E_{z}}=3.5 \)GPa
となっています。(橋本さんに合わせて強軸方向をz軸に、載荷方向をy軸にとっている。)
ちなみに、ヤング率の平均化は、\( \frac{\sum_{i=1}^{8} E_{i}\cdot\int_{A_{i}} y^2 dA_{i}}{\sum_{i=1}^{8}\int_{A_{i}} y^2 dA_{i}} \)というようにして計算すると、ぴったりこの値になります。
8層モデルについて、1枚のひき板は、橋本さんのポアソン比と同じとなるはずなので、
- \( \nu_{xy}=\nu_{xz}=\nu_{yx}=\nu_{yz}=\frac{0.4}{25}=0.016 \), \( \nu_{zx}=\nu_{zy}=0.4 \) .
ここで、\( \frac{1}{25} \)というのは、&link(対称行列にするため,http://www.str.ce.akita-u.ac.jp/~gotou/kouzou/memo.html#ihou)に$\frac{E_x}{E_z}\( や \)\frac{E_y}{E_z}$をかけているのだと思います。
1層モデルについては、\( E_{x}\neq E_{y} \)なので、ちょっと変わってきて、
- \( \nu_{xy}=\nu_{xz}=0.4\cdot\frac{\overline{E_{x}}}{\overline{E_{z}}}=0.4\cdot\frac{1.7}{3.5}\approx 0.194 \), \( \nu_{yx}=\nu_{yz}=0.4\cdot\frac{E_{y}}{\overline{E_{z}}}=0.4\cdot\frac{0.2}{3.5}\approx 0.0229 \), \( \nu_{zx}=\nu_{zy}=0.4 \)
となると思います。
また、せん断弾性係数については、橋本さんのも全方向一緒で\( G_{xy}=G_{yz}=G_{zx}=\frac{E_{z}}{15} \)としていることから、CLTの1層モデルでも、8層モデルでも
- \( G_{xy}=G_{yz}=G_{zx}=\frac{E_{z}}{15}=\frac{5}{15}\approx 0.33 \)GPa
になると思います。
近藤より(11/28)†
大体、計算の準備は整っているので、海老名君に合わせて計算しようと思います。なので、
- CLTの寸法
- 1層モデルか、8層モデルか
- 材料定数(軸の向きも)をどうしたか、具体的な値
- 荷重の大きさと載荷の範囲
- 境界条件の位置と拘束の仕方
- 変位を読み取った所(載荷面の平均値とか?)
などを日誌に書いて、合わせてCode_Asterの計算結果(とあったら手計算)も(手元にある結果からでいいので、計算できたら随時、)表にして書いておいて! ください。近藤もそこに併記しようと思っているので。
夏休みの課題†
9/26†
- 進捗状況:発表資料がまだ出来ていないので、急ぎます。
- 目標:発表資料を作成する。
9/19†
- 進捗状況:変位のデータは取れたが、比較する物が無いので、少しさびしく感じる。
- 目標:発表資料を作成する。
9/12†
- 進捗状況:具体的なモデルを作成すると、code asterが面倒なので、今回は簡単なモデルで剛性を評価する。
- 目標:変位のデータを全てまとめておく。
9/5†
- 進捗状況:簡単なモデルは作成できた。
- 目標:現場見学で実物を見ることができたので、より具体的なモデルを作成したい。
8/29†
- 進捗状況:試験体を再現できない。というよりも、設計図を読めない。
- 目標:とりあえず、簡単なモデルをつくる。
8/22†
- 目標:設計図を参考に、試験体をsalomeでモデル化する。
8/15†
8/8†
6/20†
- 断面がT字の梁の応力分布を求め、手計算と比較する。
手計算との比較†
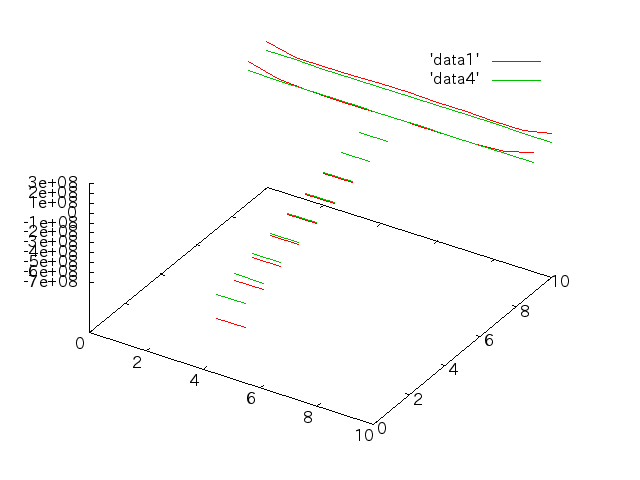
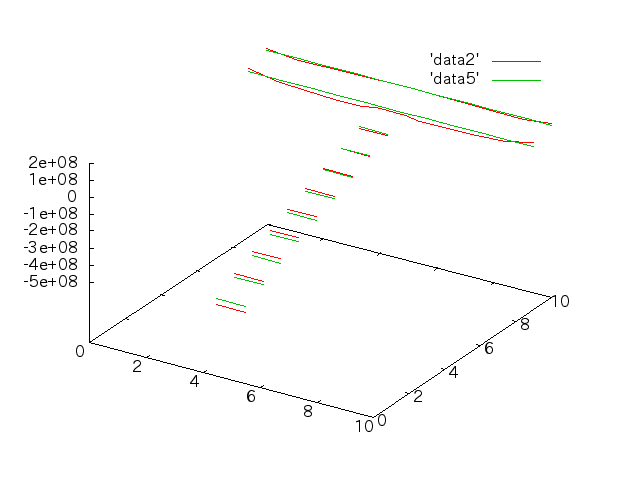
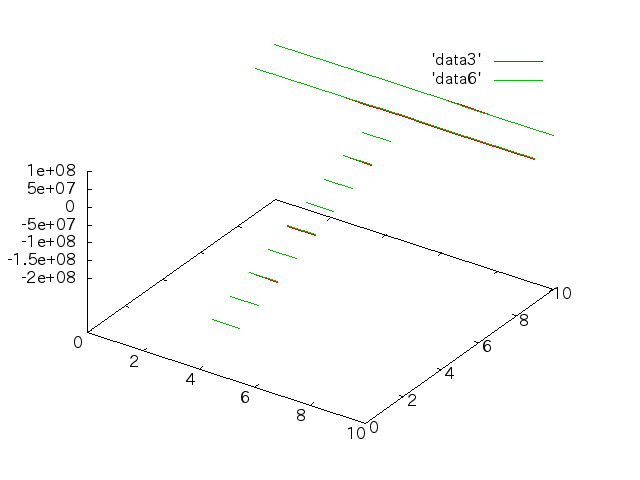
6/13†
- 梁のY方向を固定して応力分布を求め、手計算と比較する。
手計算との比較†
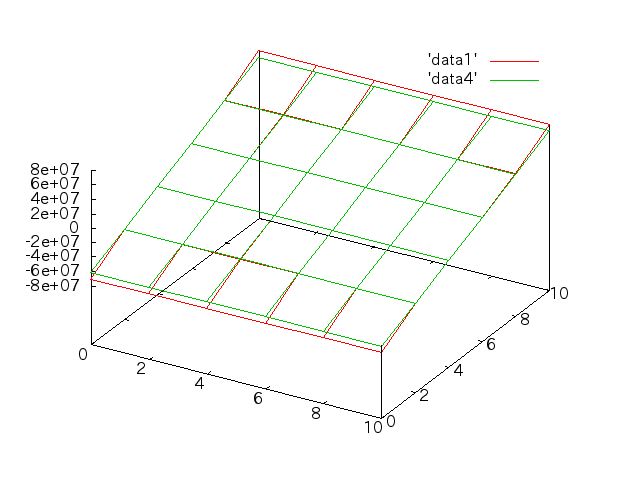
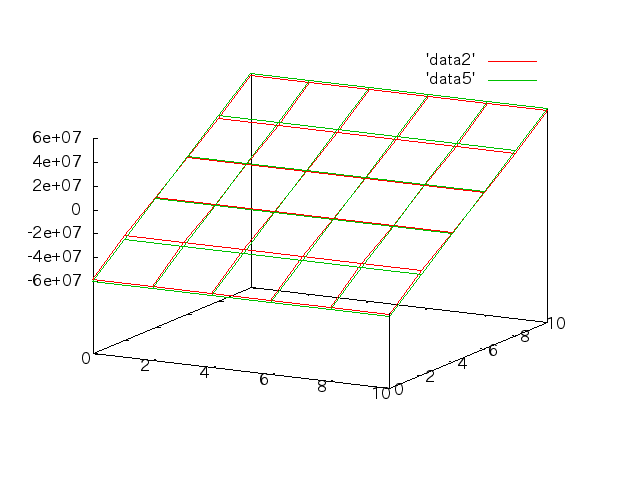
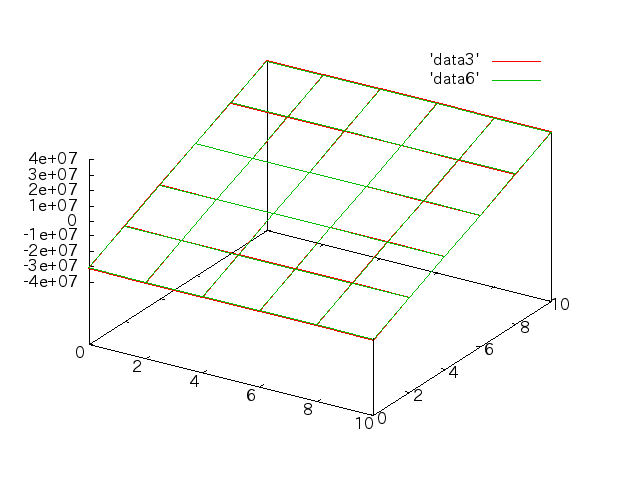
6/6†
縦軸の書き換え†
- (
real::x,y,z
character mozi*20
do i=1,6
!read*,mozi
do j=1,6
read*,x,y,z
print*,y,z,x
end do
print*
end do
end
- )
応力分布†
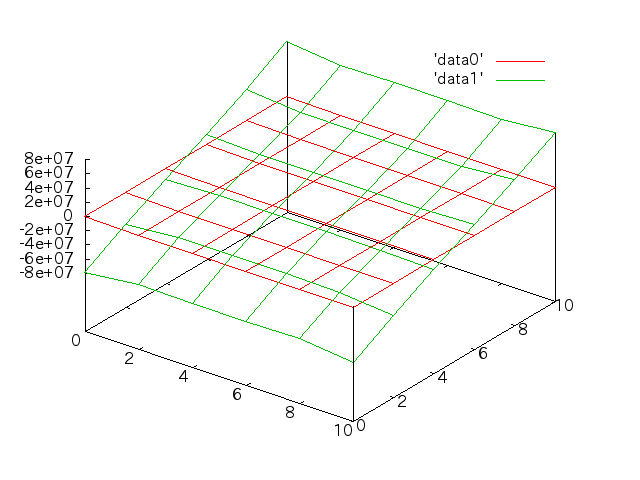
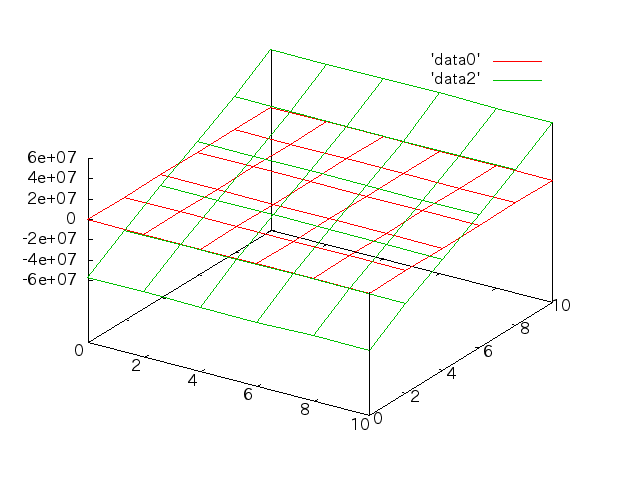
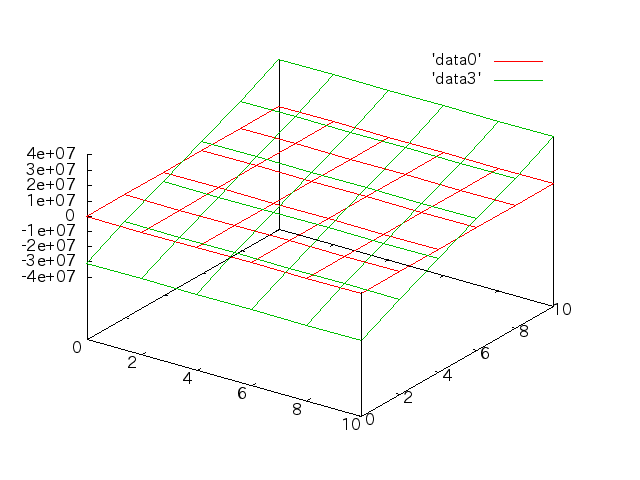

手計算との比較†
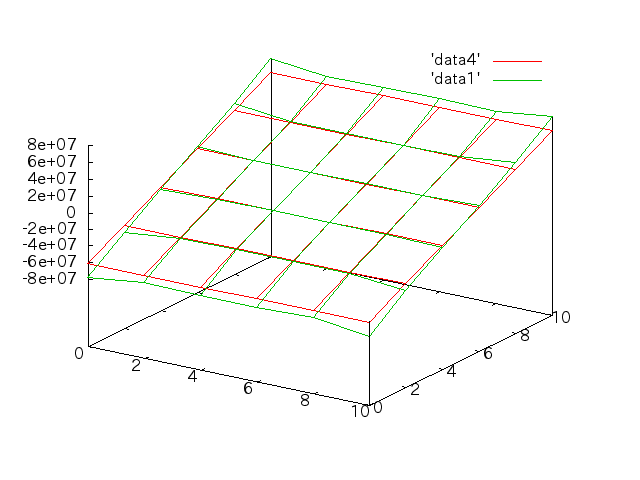
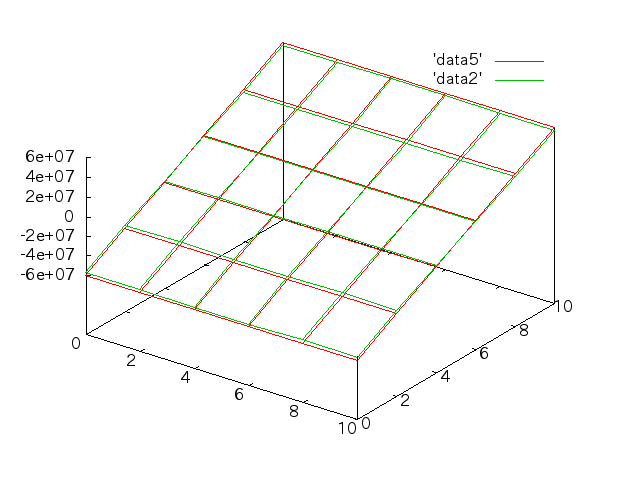
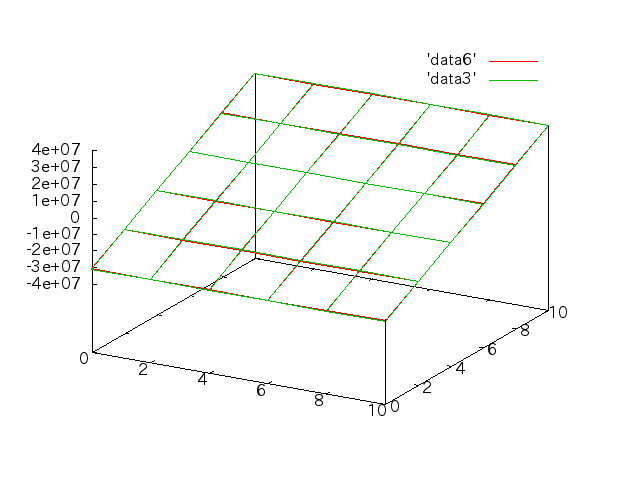
5/30†
- 先週のモデルの応力分布をグラフ化する(Mesh分割は立方体で、lengthは2mm)。
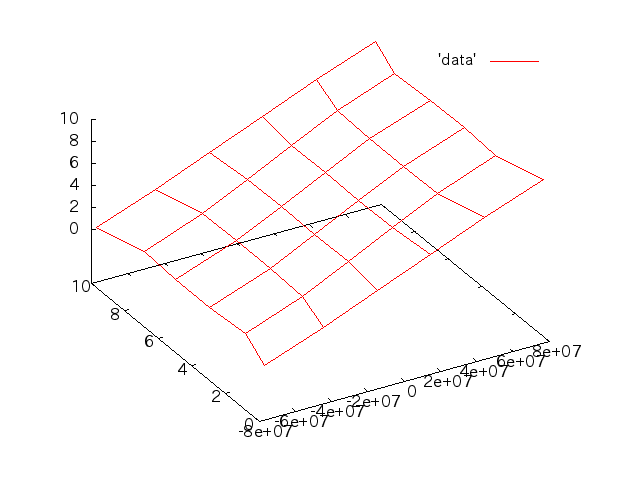
5/23†
- 先週のモデルを四面体と立方体でMesh分割し、それぞれを線形要素と2次要素について解く。
四面体(線形要素)†
| length(mm) | FEM(m) | 初等梁(m) | 相対誤差(%) | Timoshenko梁(m) | 相対誤差(%) |
| 16 | 0.00292703 | 0.00666667 | 56.1 | 0.00671867 | 56.4 |
| 8 | 0.00407108 | 0.00666667 | 38.9 | 0.00671867 | 39.4 |
| 4 | 0.00500520 | 0.00666667 | 24.9 | 0.00671867 | 25.5 |
| 2 | 0.00611654 | 0.00666667 | 8.25 | 0.00671867 | 8.96 |
| 1 | 0.00649092 | 0.00666667 | 2.64 | 0.00671867 | 3.39 |
四面体(2次要素)†
| length(mm) | FEM(m) | 初等梁(m) | 相対誤差(%) | Timoshenko梁(m) | 相対誤差(%) |
| 16 | 0.00662965 | 0.00666667 | 0.555 | 0.00671867 | 1.32 |
| 8 | 0.00664948 | 0.00666667 | 0.258 | 0.00671867 | 1.03 |
| 4 | 0.00666546 | 0.00666667 | 0.018 | 0.00671867 | 0.792 |
| 2 | 0.00667126 | 0.00666667 | 0.069 | 0.00671867 | 0.706 |
| 1 | 0.00667126 | 0.00666667 | 0.069 | 0.00671867 | 0.706 |
立方体(線形要素)†
| length(mm) | FEM(m) | 初等梁(m) | 相対誤差(%) | Timoshenko梁(m) | 相対誤差(%) |
| 2 | 0.00651456 | 0.00666667 | 2.28 | 0.00671867 | 3.04 |
| 1 | 0.00663041 | 0.00666667 | 0.544 | 0.00671867 | 1.31 |
| 0.5 | 0.00663041 | 0.00666667 | 0.544 | 0.00671867 | 1.31 |
立方体(2次要素)†
| length(mm) | FEM(m) | 初等梁(m) | 相対誤差(%) | Timoshenko梁(m) | 相対誤差(%) |
| 2 | 0.00666720 | 0.00666667 | 0.00795 | 0.00671867 | 0.766 |
| 1 | 0.00666720 | 0.00666667 | 0.00795 | 0.00671867 | 0.766 |
| 0.5 | 0.00666720 | 0.00666667 | 0.00795 | 0.00671867 | 0.766 |
5/16†
- 梁のたわみを理論式(初等梁とTimoshenko梁)と比較する。
- 初等梁v=Pl^3/3EI,Timoshenko梁v=Pl^3/3EI+Pl/kGA
- 条件:等方性材料,P=100N,E=6GPa,ν=0.3,b=10mm,h=10mm,l=100mm
| length(mm) | FEM(m) | 初等梁(m) | 相対誤差(%) | Timoshenko梁(m) | 相対誤差(%) |
| 16 | 0.00292703 | 0.00666667 | 56.1 | 0.00671867 | 56.4 |
| 8 | 0.00407108 | 0.00666667 | 38.9 | 0.00671867 | 39.4 |
| 4 | 0.00500520 | 0.00666667 | 24.9 | 0.00671867 | 25.5 |
| 2 | 0.00611654 | 0.00666667 | 8.25 | 0.00671867 | 8.96 |
| 1 | 0.00649092 | 0.00666667 | 2.64 | 0.00671867 | 3.39 |
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)