吹附の卒論日誌

卒論日誌†

作業計画†

• 1/17まで
  • メッシュを考慮しなおして計算。→1/13済
  • 適宜結果をまとめていく。

• 1/10まで
  • 昨年度までのものと同じ材料諸元して再計算。→1/6済
  • 座屈解析を行う。→1/10済

• 12/20まで
  • 試験を行う。→12/18済
  • 格子パネルのFEMを行う。→12/22済
  • 曲げ剛性の比較をする。→12/23済

FEM†

• &link(ここ,http://www.str.ce.akita-u.ac.jp/cgi-bin/gwiki/wiki.cgi?%b1%df%c5%fb%a5%d7%a5%ed%a5%b0%a5%e9%a5%e0%c3%d6%be%ec#i7)のhanikamu.f90とkousi2.f90を使ってinpファイルを作成。
• ccx_1.7で*BOUNDARY kotei,1,6にして計算。

• 格子の壁の数はハニカムの総長が930mmより \( 90m+86.603n=930 \)（\( m \)：x方向に平行な壁の数、\( n \)：y方向に平行な壁の数） の式で決定した。
  • 格子55の格子が最も正方形に近いのでこれを正方格子とする。

    	\( m \)	\( n \)	総長(mm)	総長の誤差(%)
    ハニカム	-	-	930	-
    格子55	5	5	883.015	5.05
    格子56	5	6	969.618	4.26
    格子64	6	4	886.412	4.69
    格子65	6	5	973.015	4.63
    格子73	7	3	889.809	4.32
    格子74	7	4	976.412	4.99
    格子82	8	2	893.206	3.96
    格子83	8	3	979.809	5.36
    格子91	9	1	896.603	3.59
    格子92	9	2	983.206	5.72

たわみと曲げ剛性†

• FullCure720

  ヤング率	ポアソン比
  1.4GPa	0.3

• 縦軸：\( \frac{EI}{EI正方格子} \)
• 横軸：格子55、64、73、82、91

• 実験値も合わせてプロット
  • 載荷後30分のたわみによる曲げ剛性

グラフのデータファイル（&link(itanasikousi,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/kaiseki/itanasikousi)、&link(itanasihanikamu,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/kaiseki/itanasihanikamu)、&link(3dkousi,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/kaiseki/3dkousi)、&link(3dhanikamu,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/kaiseki/3dhanikamu)）

inpファイル（&link(hanikamu.inp,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/kaiseki/inp/hanikamu.inp)、&link(55.inp,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/kaiseki/inp/55.inp)、&link(64.inp,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/kaiseki/inp/64.inp)、&link(73.inp,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/kaiseki/inp/73.inp)、&link(82.inp,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/kaiseki/inp/82.inp)、&link(91.inp,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/kaiseki/inp/91.inp)）

• アルミ
  • 材料諸元だけをアルミにして計算。

• 縦軸：\( \frac{EI}{EI正方格子} \)
• 横軸：格子55、64、73、82、91

• 比較
  • それぞれの\( \frac{EI}{EI正方格子} \)を同じグラフにプロットしてみた。
  • どうやら材料による違いはなさそう。
  • 縦軸：\( \frac{EI}{EI正方格子} \)
  • 横軸：格子55、64、73、82、91

座屈荷重†

• グラフ &link(FullCure720,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/kaiseki/720zakutu.png) &link(アルミ,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/kaiseki/arumizakutu.png)

• 縦軸：\( \frac{座屈荷重}{座屈荷重(正方格子)} \)
• 横軸：格子55、64、73、82、91

グラフのデータファイル（&link(720hanikamu,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/720hanikamu)、&link(720kousi,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/720kousi)、&link(arumihanikamu,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/arumihanikamu)、&link(arumikousi,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/arumikousi)）

Fullcure720のfrdファイル（&link(hanikamu.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/hanikamu.frd)、&link(55.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/55.frd)、&link(64.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/64.frd)、&link(73.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/73.frd)、&link(82.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/82.frd)、&link(91.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/91.frd)）

アルミのfrdファイル（&link(hanikamua.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/hanikamua.frd)、&link(55a.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/55a.frd)、&link(64a.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/64a.frd)、&link(73a.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/73a.frd)、&link(82a.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/82a.frd)、&link(91a.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/91a.frd)）

• 座屈に関しては材料によって少し違いがあるもよう。

倍率について†

• この上にはってあるfrdファイルの座屈モードは、見やすいようにそれぞれ倍率を変えてある。

• ハニカムと格子91の倍率を同じにしてみると以下のようになる。
  • 0.002のとき（&link(比較画像,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/2e-3.png)） frdファイル（&link(hanikamu-2.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/hanikamu-2.frd)、&link(55-2.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/55-2.frd)、&link(64-2.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/64-2.frd)、&link(73-2.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/73-2.frd)、&link(82-2.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/82-2.frd)、&link(91-2.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/91-2.frd)）
  • 0.002のとき（&link(比較画像,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/2e-4.png)） frdファイル（&link(hanikamu-3.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/hanikamu-3.frd)、&link(91-3.frd,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/zakutu/91-3.frd)）

FEMメモ†

いろいろ比較†

&link(この,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/kaiseki/hanikamu.inp)inpファイルの

• (

BOUNDARY†

kotei,1,6

• ) の部分をいろいろ変えて計算してみた。

• 1.7と2.3の比較
  • kotei,1,3
    • 2.3だと固定側の節点に拘束できていないところがある。
  • kotei,1,4
    • cgxで見たときのmaxとminの表示が異なっている（&link(比較画像,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/kaiseki/cgxhikaku.png)）。 左が2.3、右が1.7。 ほかのところは同じっぽいので、1.7のmaxとminの表示だけが間違っているのかな？？
  • kotei,1,6
    • 値に細かい違いがあるくらいでほかは大丈夫そう？

ヤング率†

養生7日†

• 開始0秒のひずみで初期化したものと開始30秒のひずみで初期化したもので全く同じ数値だった。

  時間(分)	たてひずみ(表)	たてひずみ(裏)	たてひずみ平均	ヤング率(GPa)	よこひずみ(表)	よこひずみ(裏)	よこひずみ平均	ヤング率(GPa)
  5	833.4002	-412.06997	210.6651	1.7542	-356.5000	115.7000	-120.4000	-3.0693
  10	842.5999	-402.8100	219.8949	1.6805	-370.4001	97.2000	-136.6001	-2.7053
  15	856.4998	-393.5500	231.4749	1.5965	-393.6001	78.7000	-157.4501	-2.3470
  20	865.8001	-384.2900	240.7551	1.5349	-412.1001	55.5000	-178.3001	-2.0726
  25	865.8001	-379.6600	243.0701	1.5203	-435.2002	37.0000	-199.1001	-1.8560
  30	870.4002	-379.6600	245.3701	1.5060	-435.2002	27.7000	-203.7501	-1.8137
  平均				1.5987				-2.3106

平均†

• &link(造形直後,http://www.str.ce.akita-u.ac.jp/cgi-bin/gwiki/wiki.cgi?%c6%a3%c5%c4%be%ad%bb%cb%a4%ce%c2%b4%cf%c0%c6%fc%bb%ef#i14)と&link(養生2日,http://www.str.ce.akita-u.ac.jp/cgi-bin/gwiki/wiki.cgi?%c4%e1%c5%c4%a4%ce%c2%b4%cf%c0%c6%fc%bb%ef#i3)、上記の養生7日のたてヤング率のそれぞれの平均を平均。

  	造形直後	養生2日	養生7日	平均
  たてヤング率(GPa)	1.138	1.447	1.5987	1.3946

その他†

• ヤング率1.4GPa。
• FEMで解くときは法線の向きを揃えてinpファイルをつくる必要がある。
• S6シェル要素。
• 試験は単純梁で行うが、解析は応力を集中させたくないので片持ち梁で。

  \( l \)	\( \frac{l}{2} \)	\( P \)	\( \frac{P}{2} \)
  180mm	90mm	500g	250g

• 厚さとかの桁数が多いとエラーが出るので適宜減らす。

試験†

結果(12/18実施)†

• スパン180mmの単純梁。
• 中央に約500gの棒状のおもりを載荷。
• 左端から1/3（60mm）のところの変位を5分ごと30分まで計測。
• 30分後、おもりを除荷しもどりの変位を5分ごと60分まで計測。

ハニカム†

格子†

曲げ剛性†

• 載荷後30分の変位をたわみとして計算した場合。

  	ハニカム	格子
  たわみ(mm)	7.21	1.29
  曲げ剛性(MN･m\( ^2 \))	7.17952915E-08	4.02061289E-07
  中央のたわみ(mm)	8.46391357E-03	1.51434785E-03

\( \frac{EIハニカム}{EI格子}=0.178568028 \)

• 載荷直後の変位をたわみとして計算した場合。

  	ハニカム	格子
  たわみ(mm)	4.38	0.78
  曲げ剛性(MN･m\( ^2 \))	1.18183578E-07	6.64947493E-07
  中央のたわみ(mm)	5.14173927E-03	9.15652257E-04

\( \frac{EIハニカム}{EI格子}=0.1777336996 \)

設計†

ハニカムパネル†

• 厚さが1mmになるように考慮してつくってみたのが&link(これ,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/honey.png)。
  • 幅：87.603mm、スパン：240.00mm、高さ：10.00mm、厚さ：1.00mm
  • 試験は左右30mmずつ装置にのせて行うので、スパンは180mmとなる。

格子パネル†

• ハニカムパネルと総長や材料重量が同じになるようにしたい。
• まず総長を同じくらいになるようにしていくつかつくってみた。
  • x方向に平行な壁の数をm、y方向に平行な壁の数をnとして 240m+86.603n=248 の式に当てはめて壁の数を決める。
• 幅：86.603mm、スパン：240.00mm、高さ：10.00mm、厚さ：1.00mm。
  • ハニカムは端っこに厚みがつくので幅は格子の方が1mm小さい。

    	ハニカム	格子49	格子77	格子87	格子78	格子88	格子145	格子174	格子203
    x方向に平行な壁の数	-	9	7	7	8	8	5	4	3
    y方向に平行な壁の数	-	4	7	8	7	8	14	17	20
    総長(cm)	248	251	229	238	253	262	243	245	247
    体積(cm\( ^{3}) \)	25.701	24.744			24.772	25.568	23.565
    総長の誤差(%)	-						2.72

• スパン180mmでみた時

  	ハニカム	格子145
  総長(cm)	186	176.603
  総長の誤差(%)	-	5.05
  体積(cm\( ^{3}) \)	19.281	17.160

• FEMで解くときのことを考えて、壁の総長を同じにして格子パネルをつくる。

• ハニカムパネルと比較するために、正方格子に近いもの(&link(格子145,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/145-2.png))で作成。

試作品†

完成版(13/7/19)†

• 厚みがない（？）のが原因っぽかったのでSALOMEで厚さを考慮してつくったのが&link(これ,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/honey10-9.png)。
  • 幅：8.314cm、スパン：17.100cm、高さ：1cm
• 今回は厚さを持たせるために無理やり（対角長20mmと18mmの正六角形を組み合わせた）つくったのでものすごく中途半端な厚さになってしまった。
  • 厚さ：0.866mm
• 3Dプリンタで印刷することに成功。

試作版†

その２(13/7/16)†

• 剛性が大きくなる向きを考慮してつくってみたのが&link(これ,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/5itaari.png)。 ハニカム一つ(正六角形)の大きさは、対角長2cm、対辺の距離\( \sqrt3 \)cm。 （幅：\( 5\sqrt3 \)(≒8.660)cm、スパン：18cm、高さ：1cm）
• 上下に板がないものは&link(こんな,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/5itanashi.png)感じ。

後藤ちゃちゃ(13/7/15)†

ハニカムは六角形の平行な対辺が梁軸方向を向く &link(こんな,http://www.str.ce.akita-u.ac.jp/~gotouhan/tamegai/2012/hani96.png) 向きにした方が剛性が大きくなるので、剛性が大きくなる向きで作りましょう。

その１(13/7/12)†

• ハニカム一つ(正六角形)の大きさを、対角長2cm、対辺の距離\( \sqrt3 \)cmとする。
• SALOMEとFreeCADでつくってみたのが&link(こんな,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/11itaari.png)感じ。 （幅：9cm、スパン：\( 11\sqrt3 \)(≒19.053)cm、高さ：1cm）
• 3Dプリンターで形成するとき浮いている部分はサポート材で支えながらつくるので、このように閉じているものをつくったら中身がどうなるのかがわからない（ものづくりセンターの人に問い合わせてみる）。
• ので一応&link(上下に板がないもの,http://www.str.ce.akita-u.ac.jp/~gotouhan/fukitsuke/11itanashi.png)もつくっておく。

その他†

• ものづくりセンターの人に聞いてみたところ、上下に板がついていて閉じていると中にサポート材が残ってしまうそう。
• ということで3Dプリンターでハニカムパネルをつくる場合は上下に板がないものになりそうです。

• 試作品その１とその２のstlファイルを印刷しようとしたところ、Objet Studio上で以下のように表示され印刷できなかった。 （&link(この,http://www.cs.dartmouth.edu/~robotics/oldwiki/index.php/Objet_Eden_250)ページにこれについてちょっと書いてある。）
  • ( Unclosed contours are detected!
  • )
• 厚さがない（？）のが原因？？

パソコンゼミ†

6/17までの課題†

グラフ†

• 前回の課題の片持ち梁と同様の条件でやってみる。
• 荷重：10kg(9.81×10^-5[MN])

• 梁断面縦長
  • 桁幅：0.01m、桁高：0.02m、梁の軸長：0.2m
  • 理論値：0.013182024m
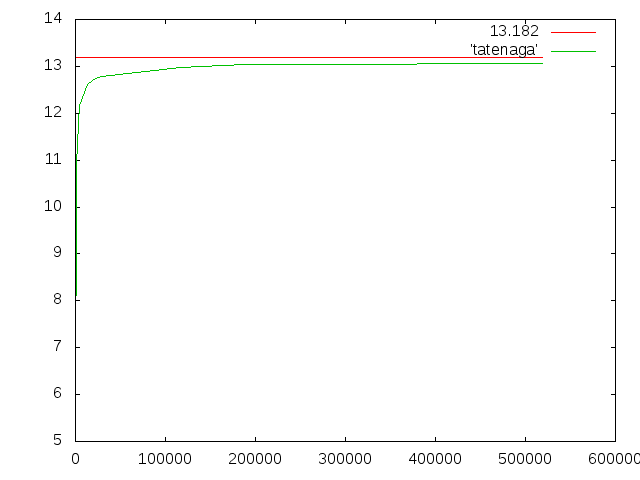
    • 横軸：要素数(Element)
    • 縦軸：たわみ(mm)

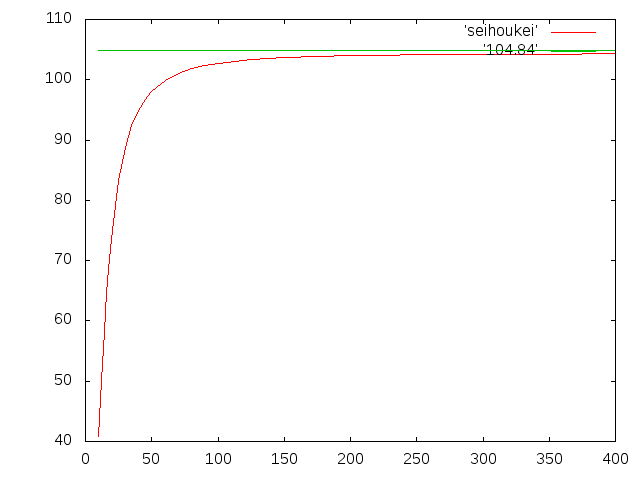
• 梁断面正方形
  • 桁幅：0.01m、桁高：0.01m、梁の軸長：0.2m
  • 理論値：0.1048444048m
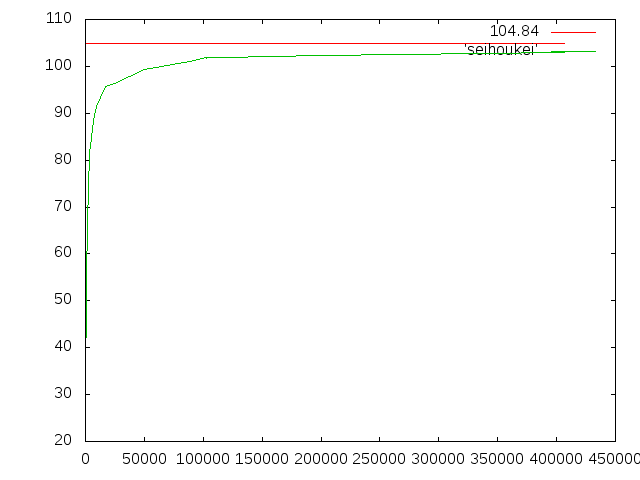
    • 横軸：要素数(Element)
    • 縦軸：たわみ(mm)

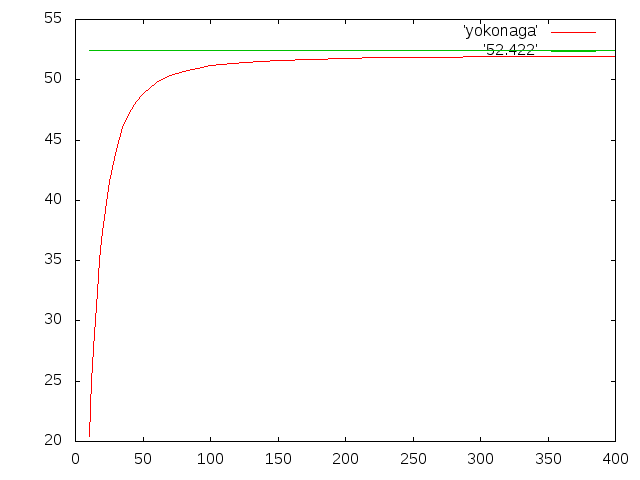
• 梁断面横長
  • 桁幅：0.02m、桁高：0.01m、梁の軸長：0.2m
  • 理論値：0.052422024m
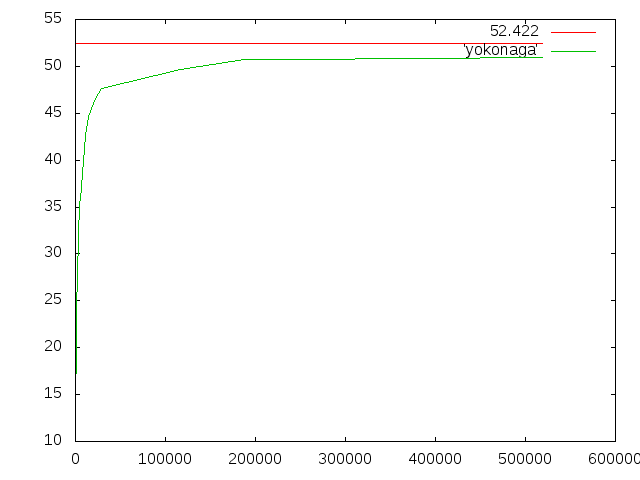
    • 横軸：要素数(Element)
    • 縦軸：たわみ(mm)

相対誤差†

SALOMEでのスケールについて†

• SALOMEで1mを0.001としたとき
  • &link(CAELinuxのFEM解法,http://www.str.ce.akita-u.ac.jp/cgi-bin/gwiki/wiki.cgi?CAELinux%a4%ceFEM%b2%f2%cb%a1)の諸注意に書いてあるようにSalome上で1mの長さを0.001として（つまりDx=0.00001、Dy=0.0002、Dz=0.00001とした）計算したところ、出てきた値の桁がなんか変。結果の単位はmのはずだよな？結果は以下の通り。

    Length	vx
    2.0e-05	2.8869E+01
    1.0e-05	5.9501E+01
    0.8e-05	6.2844E+01
    0.5e-05	8.0833E+01
    0.4e-05	8.2250E+01
    理論値	1.0484E-01

• SALOMEで1mを1.0としたとき
  • というわけで、1mの長さを1.0として（今度はDx=0.01、Dy=0.2、Dz=0.01とした）計算したところそれっぽい値が出た。
  • 長方形断面でも同様（Dx=0.01、Dy=0.2、Dz=0.02）にやってみたところ、それっぽい。

    Length	Element	正方形(vx)		Element	横長(vx)	縦長(vz)
    0.02	258	2.4538E-02		219	1.1439E-02	5.2989E-03
    0.01	1230	5.9356E-02		1383	2.3045E-02	1.0892E-02
    0.006	3403	8.1170E-02		4721	3.5462E-02	1.2186E-02
    0.0033				10607	4.2628E-02	1.2512E-02
    0.0032	4473	8.2948E-02
    0.0031	6369	8.8506E-02		14861	4.4683E-02	1.2641E-02
    0.003	8986	9.1532E-02		22494	4.6575E-02	1.2746E-02
    0.002	16772	9.5680E-02		29407	4.7656E-02	1.2780E-02
    0.0015	24270	9.6421E-02		116439	4.9631E-02	1.2978E-02
    0.00145	50027	9.9432E-02
    0.0013	88174	1.0111E-01
    0.001	102498	1.0179E-01		187860	5.0697E-02	1.3036E-02
    0.00075	117032	1.0187E-01		240683	5.0767E-02	1.3042E-02
    0.00074				518959	5.0971E-02	1.3058E-02
    0.0006	406475	1.0306E-01
    理論値	---	1.0484E-01		---	5.2422E-02	1.3182E-02

• なんかややこしい荷重でやってるので、これで合っているか真偽は不明。どなたか情報求む。

メモ†

• ところで結果はNsaikaの数だけ出てくるわけだけど、どの値をたわみとしたらいいのだろう？平均をとったほうがいいのかもと思いつつも、上記はとりあえず最大の値を結果とした。
• 分割数が多くなってくるとどの点でも同じような値が出るようになる。

6/10までの課題†

アクリル材(ヤング率3GPa、ポアソン比0.3)の片持ち梁で、梁断面３種。 荷重は10kg(9.81×10^-5[MN])。

• 梁断面縦長
  • 桁幅：0.01m、桁高：0.02m、梁の軸長：0.2m
  • 理論値：0.013182024m
  • nx=10、ny=20でnzのみを変化させる。
    • 横軸：要素数(nz)
    • 縦軸：たわみ(mm)

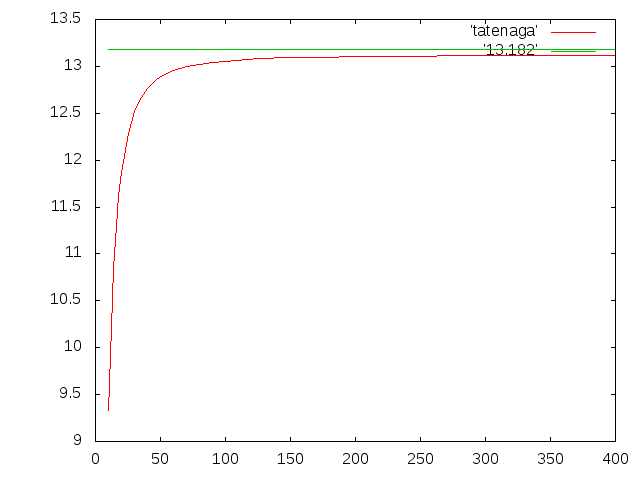
• 梁断面正方形
  • 桁幅0.01m、桁高0.01m、梁の軸長0.2m
  • 理論値：0.1048444048m
  • nx=10、ny=20でnzのみを変化させる。
    • 横軸：要素数(nz)
    • 縦軸：たわみ(mm)

• 梁断面横長
  • 桁幅：0.02m、桁高：0.01m、梁の軸長：0.2m
  • 理論値：0.052422024m
  • nx=10、ny=20でnzのみを変化させる。
    • 横軸：要素数(nz)
    • 縦軸：たわみ(mm)

相対誤差†

6/3までの課題†

• 幅0.02m、高さ0.01m、長さ0.2mのアクリル材(ヤング率3GPa)の片持ち梁を考える。
• 荷重は10kg(9.81×10^-5[MN])とした。
• 手計算\( \frac{P\ell^{3}}{3EI} \)の結果は0.05232[m]。

  nx	ny	nz	たわみ
  10	5	100	3.4255E-02
  10	5	200	3.4663E-02
  10	5	400	3.4767E-02
  20	10	100	4.8186E-02
  20	10	200	4.8766E-02
  20	10	400	4.8915E-02

• x方向とy方向の分割数を増やすと手計算の値に近づいていくのがわかる。そこでもっと分割しようとしたところ、最後まで計算してもらえなかった(やり方が悪いのかな？)。
• cgxで図を描いてみようとしたら、以下のように表示されてできなかった。なんでだろう…？？？
  • ( cgx: via_tex.c:427: viaSwapOutWork: Assertion `sz == vmesa->total_alloc[heap]' failed. アボートしました
  • )

最新の100件