座標は、梁軸方向に$z$, たわみ方向に$y$を取る。
二次元の梁の問題は黒板を$yz$平面として考える。
座標は、梁軸方向に$z$, たわみ方向に$y$を取る。
二次元の梁の問題は黒板を$yz$平面として考える。
注意: このページの数式は、 MathJaxを使って書いてます。 数式部分がおかしい場合は、更新ボタンをクリックすると 改善するかも知れません。 あと、おかしい記述があると思ったら、 メールなどで指摘して下さい。
「変位」というのは、着目している点がどこに移動したかということで、 「変形」というのは、着目している物体の形が変わること。 物体の形がほとんど変形せずに、遠くまで変位することもあれば、 物体がある場所に留まってぐしゃっと大きく変形することもある。 つまり、「変位」と「変形」は違う。 この点が横の方にすごく変位したとか、 この棒がぐにゃっとすごく変形したとかいうのを 数値(とか座標の関数とか)で表すにはどうしたらいいだろう。
 座標は、梁軸方向に$z$, たわみ方向に$y$を取る。
二次元の梁の問題は黒板を$yz$平面として考える。
座標は、梁軸方向に$z$, たわみ方向に$y$を取る。
二次元の梁の問題は黒板を$yz$平面として考える。
 物体が外力を受けずに変位も変形もせずに静止している状態を
初期状態と呼んでおく。
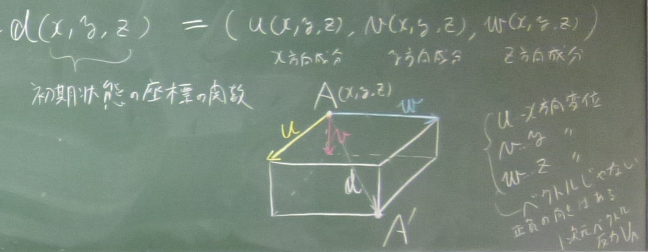
初期状態で点$A(x,y,z)$にあった物体内の点が、
$x$方向に$u$だけ,
$y$方向に$v$だけ,
$z$方向に$w$だけそれぞれ変位したとする。
点$A$の変位を表すベクトル
$\mathbf{d}(x,y,z)=(u(x,y,z),v(x,y,z),w(x,y,z))$を
点$A$の変位ベクトルと言う。
これは初期状態の座標$(x,y,z)$の関数になっている。
つまり、初期状態で$(x,y,z)$にあった点$A$が、変形後に
そこからどの方向にどれだけ移動したかを
表しているのが点$A$の変位ベクトルである。ただし、
ベクトルの成分$u,v,w$
(それぞれ$x$方向変位、$y$方向変位、$z$方向変位)は、方向が決まっているので、
ベクトルではない。
方向が決まっていて正負の区別がある
1次元ベクトルとして扱う
(反力$V_{A}$とかの扱いと同じ)。
物体が外力を受けずに変位も変形もせずに静止している状態を
初期状態と呼んでおく。
初期状態で点$A(x,y,z)$にあった物体内の点が、
$x$方向に$u$だけ,
$y$方向に$v$だけ,
$z$方向に$w$だけそれぞれ変位したとする。
点$A$の変位を表すベクトル
$\mathbf{d}(x,y,z)=(u(x,y,z),v(x,y,z),w(x,y,z))$を
点$A$の変位ベクトルと言う。
これは初期状態の座標$(x,y,z)$の関数になっている。
つまり、初期状態で$(x,y,z)$にあった点$A$が、変形後に
そこからどの方向にどれだけ移動したかを
表しているのが点$A$の変位ベクトルである。ただし、
ベクトルの成分$u,v,w$
(それぞれ$x$方向変位、$y$方向変位、$z$方向変位)は、方向が決まっているので、
ベクトルではない。
方向が決まっていて正負の区別がある
1次元ベクトルとして扱う
(反力$V_{A}$とかの扱いと同じ)。
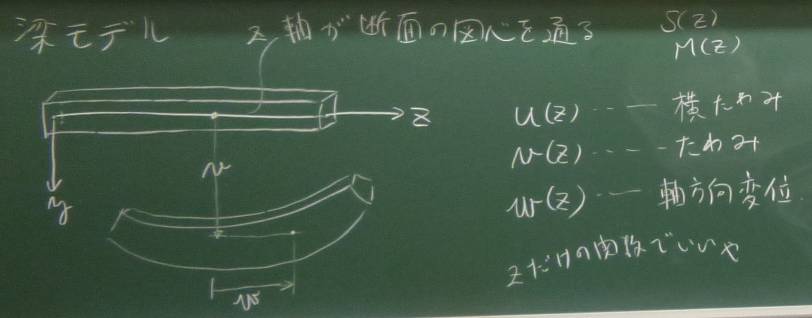 後述するが、梁モデルの場合、断面の図心をつらねた線を$z$軸として、
断面内の$x,y$座標が違う場所の変位の違いはそれほど大きくないので、
以下のように各変位は$z$だけの関数として扱う。
後述するが、梁モデルの場合、断面の図心をつらねた線を$z$軸として、
断面内の$x,y$座標が違う場所の変位の違いはそれほど大きくないので、
以下のように各変位は$z$だけの関数として扱う。
$u(z)$ 横たわみ
$v(z)$ たわみ
$w(z)$ 軸方向変位
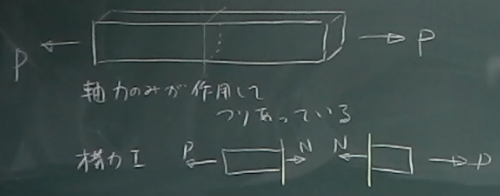
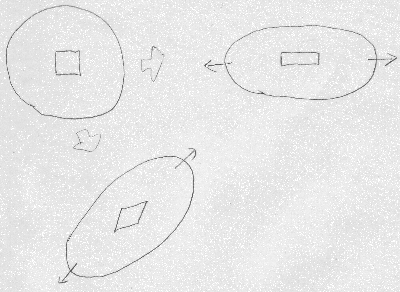 変形には「伸び縮み変形」と「せん断変形」がある。
まず、
物体の中に各辺が座標軸と平行な微小な立方体(2次元なら正方形)の要素を
考えて、その四角い要素がどのように変形するかということに
着目してみる。
簡単のため2次元で考えるとして、
例えば、図のような物体が左右に引っ張られたとして、
微小正方形要素の周辺が$z$軸方向には一様に伸び、
$y$方向には一様に縮んだとすると、
正方形要素は、頂点の直角を保ったまま長方形に変形する。
このように、物体中の微小な立方体(2次元なら正方形)要素が、
頂点の直角を保ちながら、直方体(2次元なら長方形)に変形するような変形を、
ここでは「伸び縮み変形」と呼んでおく。
一方、図のような物体を微小正方形の対角線方向に斜めに引っ張ったら、
微小正方形要素は、頂点の直角がくずれて、ひし形に変形するだろう。
このように物体中の微小な立方体(2次元なら正方形)要素が、
(辺の長さは変えずに)頂点の角度を変えるような変形を「せん断変形」と呼ぶ。
すると、これ以外の一般的な変形
(図の微小正方形が不等辺の平行四辺形になるような)も、
「伸び縮み変形」と「せん断変形」の組合せとして表せそうだ。
変形には「伸び縮み変形」と「せん断変形」がある。
まず、
物体の中に各辺が座標軸と平行な微小な立方体(2次元なら正方形)の要素を
考えて、その四角い要素がどのように変形するかということに
着目してみる。
簡単のため2次元で考えるとして、
例えば、図のような物体が左右に引っ張られたとして、
微小正方形要素の周辺が$z$軸方向には一様に伸び、
$y$方向には一様に縮んだとすると、
正方形要素は、頂点の直角を保ったまま長方形に変形する。
このように、物体中の微小な立方体(2次元なら正方形)要素が、
頂点の直角を保ちながら、直方体(2次元なら長方形)に変形するような変形を、
ここでは「伸び縮み変形」と呼んでおく。
一方、図のような物体を微小正方形の対角線方向に斜めに引っ張ったら、
微小正方形要素は、頂点の直角がくずれて、ひし形に変形するだろう。
このように物体中の微小な立方体(2次元なら正方形)要素が、
(辺の長さは変えずに)頂点の角度を変えるような変形を「せん断変形」と呼ぶ。
すると、これ以外の一般的な変形
(図の微小正方形が不等辺の平行四辺形になるような)も、
「伸び縮み変形」と「せん断変形」の組合せとして表せそうだ。
上の例では、微小正方形要素の各辺が座標軸と平行になるような要素を
考えることにしたが、もし微小正方形要素を45°回転させたら、
今度は、左右に引っ張るとせん断変形して、
右上と左下の斜め方向に引っ張ると伸び縮み変形するようにもできる。
つまり、伸び縮み変形とかせん断変形というのは、
どの座標系で観測するかに依存して変わってくるものであるし、
逆に言うと、どんな変形状態でも伸び縮み変形として捉えることのできる
向きがあることになる(この辺の話は「主ひずみ」の話をする機会が
あれば後述)。
 変形を数値で表すには、「ひずみ」という物理量を使う。
伸び縮み変形を表すには、1つの点の変位だけを調べても、
その点がどれだけ動いたかはわかっても、
その点の周囲がどれだけのびたかはわからない。
だから、2つの点の変位を調べて、2つの点の距離が最初の状態から、
のびたか縮んだかで変形の程度を表したい。
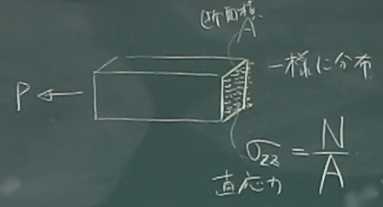
図のように初期状態で$z$軸に横たわる細長い棒があったとして、
その棒の微小部分$dz$に着目する。
初期状態でこの棒の左端が$z$にあるとすると、右端は$z+dz$にあることになる。
さて、この棒が外力を受けて変形しながら変位し、
左端が$w(z)$だけ、右端が$w(z+dz)$だけ変位したとする。
その結果、微小部分$dz$が初期状態よりちょっとだけ伸びたとする。
その初期状態よりちょっとだけ伸びた比率を、
直ひずみ$\varepsilon_{zz}$という量で表したい
($zz$という添字は、$z$方向の直ひずみということ。
「直ひずみ」というのは伸び縮み変形を表すひずみのことで、
$\varepsilon_{z}$みたいに添字は$z$1文字でもいいのだが、
せん断変形を表すせん断ひずみは、
添字が2文字になるので、それに合わせておく)。
つまり元の長さが$dz$だった微小部分が、
伸びて$dz(1+\varepsilon_{zz})$になったとした場合の、
$\varepsilon_{zz}$を両端の変位$w$を使って表したい。
変形を数値で表すには、「ひずみ」という物理量を使う。
伸び縮み変形を表すには、1つの点の変位だけを調べても、
その点がどれだけ動いたかはわかっても、
その点の周囲がどれだけのびたかはわからない。
だから、2つの点の変位を調べて、2つの点の距離が最初の状態から、
のびたか縮んだかで変形の程度を表したい。
図のように初期状態で$z$軸に横たわる細長い棒があったとして、
その棒の微小部分$dz$に着目する。
初期状態でこの棒の左端が$z$にあるとすると、右端は$z+dz$にあることになる。
さて、この棒が外力を受けて変形しながら変位し、
左端が$w(z)$だけ、右端が$w(z+dz)$だけ変位したとする。
その結果、微小部分$dz$が初期状態よりちょっとだけ伸びたとする。
その初期状態よりちょっとだけ伸びた比率を、
直ひずみ$\varepsilon_{zz}$という量で表したい
($zz$という添字は、$z$方向の直ひずみということ。
「直ひずみ」というのは伸び縮み変形を表すひずみのことで、
$\varepsilon_{z}$みたいに添字は$z$1文字でもいいのだが、
せん断変形を表すせん断ひずみは、
添字が2文字になるので、それに合わせておく)。
つまり元の長さが$dz$だった微小部分が、
伸びて$dz(1+\varepsilon_{zz})$になったとした場合の、
$\varepsilon_{zz}$を両端の変位$w$を使って表したい。
幾何学的な関係から、
$dz(1+\varepsilon_{zz})=dz+w(z+dz)-w(z)$
であるから、これを整理すると、
${\displaystyle \varepsilon_{zz}=\frac{w(z+dz)-w(z)}{dz}
}$
と書けるが、
これは$dz$がじゅうぶんに微小だという仮定のもとでの
ひずみのおおざっぱな定義である。
微小部分の長さ$dz$を極限まで小さくしてやると
これは「微分」の定義になるので、
ある点$(x,y,z)$の
$z$方向の直ひずみは次式のように$z$方向変位の$z$に関する微分として
定義できる。
$
{\displaystyle
\varepsilon_{zz}(z)=\lim_{dz \to 0}\frac{w(z+dz)-w(z)}{dz}
=\frac{d w(z)}{dz}=w'(z)
}
$
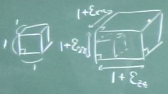 $z$軸に横たわる梁の問題では、
$x$方向や$y$方向の直ひずみは無視できるが、
3次元の物体の変形の問題では、
$x$方向の直ひずみ$\varepsilon_{xx}$や
$y$方向の直ひずみ$\varepsilon_{yy}$も同様に定義できる。
(ここで定義した$\varepsilon_{zz}(z)$は厳密には、
梁の断面の図心位置での$z$方向直ひずみということになる。
下の方の梁モデルのところで少し述べるが、
直ひずみは場所によって異なるので厳密には
$\varepsilon_{zz}(x,y,z)$みたいに$x,y,z$に依存する)。
$z$軸に横たわる梁の問題では、
$x$方向や$y$方向の直ひずみは無視できるが、
3次元の物体の変形の問題では、
$x$方向の直ひずみ$\varepsilon_{xx}$や
$y$方向の直ひずみ$\varepsilon_{yy}$も同様に定義できる。
(ここで定義した$\varepsilon_{zz}(z)$は厳密には、
梁の断面の図心位置での$z$方向直ひずみということになる。
下の方の梁モデルのところで少し述べるが、
直ひずみは場所によって異なるので厳密には
$\varepsilon_{zz}(x,y,z)$みたいに$x,y,z$に依存する)。
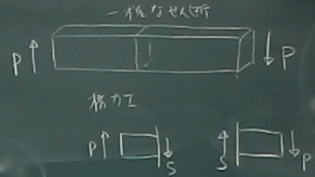
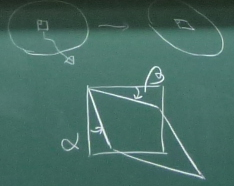 せん断変形を数値で表すには
「せん断ひずみ」という物理量を使う。
図のように初期状態で長方形だった物体内の微小部分が、
変形後に平行四辺形につぶれた(せん断変形した)とする。
このとき、ある頂点の2辺が内側にそれぞれ角度$\alpha$, $\beta$だけ
回転して変形したとすると、この平面($yz$面)のせん断ひずみは、
せん断変形を数値で表すには
「せん断ひずみ」という物理量を使う。
図のように初期状態で長方形だった物体内の微小部分が、
変形後に平行四辺形につぶれた(せん断変形した)とする。
このとき、ある頂点の2辺が内側にそれぞれ角度$\alpha$, $\beta$だけ
回転して変形したとすると、この平面($yz$面)のせん断ひずみは、
せん断ひずみ:
${\displaystyle
\varepsilon_{yz}=\frac{\alpha+\beta}{2}
}$
で表される。
角度$\alpha$, $\beta$を点の変位から求めるためには、
3つの頂点の変位に着目する必要がある。
梁モデルでは、
断面の図心をつらねた軸の変位($u, v, w$)しか考えないので、
こうした3点の変位とせん断ひずみを関係づけることはしないが、
2次元の物体内の点の変位とせん断ひずみとの関係について、
ちゃんと知りたい場合は、こちらを参照。
なお、$\alpha+\beta$を2で割らずにそのまま「せん断ひずみ」と
呼ぶ場合もあるので注意が必要である。
区別しないと混乱を招くので、2で割らない場合は
「工学的せん断ひずみ」や「工学せん断ひずみ」
と呼ぶ。
工学的せん断ひずみの記号は、$\gamma$が使われることが多いが、
$\varepsilon$が使われることもあるので、
文献中に
せん断ひずみが現れたら、
式中の係数等から2で割ったせん断ひずみか工学せん断ひずみかを判断する
必要がある。
工学せん断ひずみ:
$\gamma_{yz}=\alpha+\beta$
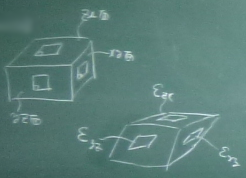 3次元の物体の変形の問題では、
$zx$面のせん断ひずみ$\varepsilon_{zx}$や
$xy$面のせん断ひずみ$\varepsilon_{xy}$も同様に定義できる。
もっとも、細長い梁の問題では、
どのせん断ひずみも無視できるが(詳しくは後述)。
3次元の物体の変形の問題では、
$zx$面のせん断ひずみ$\varepsilon_{zx}$や
$xy$面のせん断ひずみ$\varepsilon_{xy}$も同様に定義できる。
もっとも、細長い梁の問題では、
どのせん断ひずみも無視できるが(詳しくは後述)。
以下は、ひとまず箇条書き的にメモしていきます
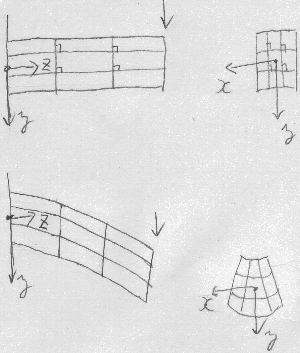 割と太短い棒の場合、図のように棒の側面に直角な枡目を描いておいて
曲げてやると、曲げを受ける平面内でせん断変形が生じて枡目の角は直角では
なくなるだろう。また棒の断面についても、
例えば引っ張られる上辺は軸方向に伸びたぶん幅方向には縮んだり、
圧縮される下辺は軸方向に縮んだぶん幅方向には膨れたりといった変形も
生じるかも知れない。
これらの変形を考慮すると式の導出がなかなか繁雑になってしまうので
(もちろん、それらを考慮すべき場合は、
考慮して繁雑な式を導出すべきだろうが)、
ここではまず簡単な問題として、上記の変形が無視できるような
「非常に細長い棒が、ちょっとだけ曲がる」
場合に限定して考えたい。
という訳で次の2つの仮定を設けることにする。
割と太短い棒の場合、図のように棒の側面に直角な枡目を描いておいて
曲げてやると、曲げを受ける平面内でせん断変形が生じて枡目の角は直角では
なくなるだろう。また棒の断面についても、
例えば引っ張られる上辺は軸方向に伸びたぶん幅方向には縮んだり、
圧縮される下辺は軸方向に縮んだぶん幅方向には膨れたりといった変形も
生じるかも知れない。
これらの変形を考慮すると式の導出がなかなか繁雑になってしまうので
(もちろん、それらを考慮すべき場合は、
考慮して繁雑な式を導出すべきだろうが)、
ここではまず簡単な問題として、上記の変形が無視できるような
「非常に細長い棒が、ちょっとだけ曲がる」
場合に限定して考えたい。
という訳で次の2つの仮定を設けることにする。
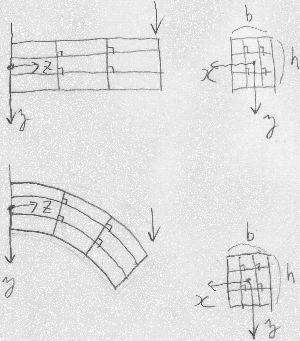
これらの仮定を満たす棒のことをベルヌーイ・オイラー梁 (Bernoulli-Euler梁)とか初等梁と言う。 このテキストで特に注意書きなしで「梁」と書く場合は 初等梁のことを指す。 ちなみに、 ティモシェンコ梁(Timoshenko梁)は、 曲げを受ける平面内のせん断変形を考慮した梁である。
さて、ベルヌーイ・オイラーの仮定と 断面形不変の仮定をすると、ほとんどのひずみ成分は0になってしまい、 考えなくてよい。 0でないひずみは、軸方向の直ひずみ$\varepsilon_{zz}$だけである。 つまり、 初等梁では、ひずみとして、 $\varepsilon_{zz}$だけを扱えばいいので、 だいぶ、話が簡単になる。
 さて、初等梁では、軸方向の直ひずみ$\varepsilon_{zz}$しか生じないのだが、
断面の各部分が軸方向にしか伸び縮みしないのに、
そんなんで、梁全体はどうやって曲がるんだろうか。
右の絵のように、梁の上の方はちょっとしか伸びなくて(あるいは縮んで)、
梁の下の方がいっぱい伸びると、梁は曲がるのだ。
実際の細長い棒でも、そういうことが起きていると考えられる。
さて、初等梁では、軸方向の直ひずみ$\varepsilon_{zz}$しか生じないのだが、
断面の各部分が軸方向にしか伸び縮みしないのに、
そんなんで、梁全体はどうやって曲がるんだろうか。
右の絵のように、梁の上の方はちょっとしか伸びなくて(あるいは縮んで)、
梁の下の方がいっぱい伸びると、梁は曲がるのだ。
実際の細長い棒でも、そういうことが起きていると考えられる。
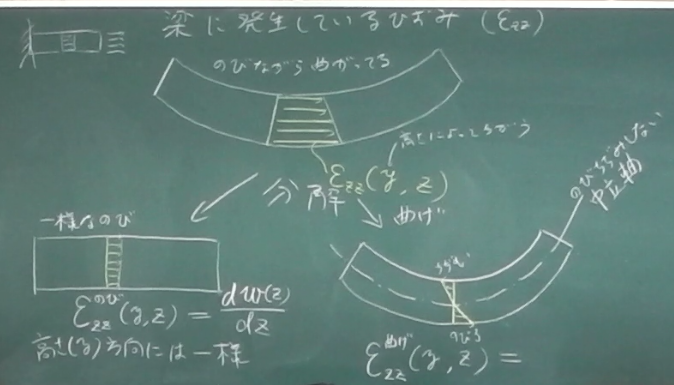
そうすると、直ひずみ$\varepsilon_{zz}$は、断面の上の方と下の方とで、 大きさが違うから$\varepsilon_{zz}(y,z)$みたいに、高さ$y$にも依存する 関数として与えなければならない。 このページの上の方で、 せっかく 梁の断面の変位は図心で代表させて、 $v(z), w(z)$みたいに図心を通る$z$座標だけの関数で表すことにしたのに、 直ひずみ$\varepsilon_{zz}(y,z)$が断面の高さ$y$に依存するのは ちょっとやっかいだ。 直ひずみ$\varepsilon_{zz}(y,z)$を図心変位$v(z), w(z)$を使って表したいが、 そんなことができるだろうか。
というわけで、まずは、直ひずみ$\varepsilon_{zz}(y,z)$を 右上の絵のような一様な伸び成分 $\varepsilon_{zz}^{のび}(y,z)$ と一様な曲げ成分 $\varepsilon_{zz}^{曲げ}(y,z)$ との足し算で表せるように分解してやる。 実際の直ひずみ$\varepsilon_{zz}(y,z)$の分布は、 上の方がちょっとだけ伸びて、下の方がいっぱい伸びてという 台形分布をしているのだけど、 これを上から下まで一様な伸びの成分 と 図心位置ではのびちぢみがなく上がちぢんで下がのびてる成分との 足し算に分解するのだ。
そうすると、 まず直ひずみの伸び成分 $\varepsilon_{zz}^{のび}(y,z)$については、 高さ$y$によらずに断面のどの高さでも値は同じなのだから、 これは上の方で定義した図心位置の軸方向変位を用いた 図心位置の直ひずみ$\varepsilon_{zz}(z)=w'(z)$を使って、 $\varepsilon_{zz}^{のび}(y,z)=w'(z)$と表せるだろう。
 では、直ひずみの曲げ成分
$\varepsilon_{zz}^{曲げ}(y,z)$については、
図心変位の$v(z)$や$w(z)$を使って表せるだろうか。
右の絵のように、
初期状態の梁の微小なスライスを考える。
この微小なスライスが梁の変形後、
上の方は縮んで、図心位置($y=0$)は伸び縮みせず、
下の方は伸びてバームクーヘン状になったものとする。
では、直ひずみの曲げ成分
$\varepsilon_{zz}^{曲げ}(y,z)$については、
図心変位の$v(z)$や$w(z)$を使って表せるだろうか。
右の絵のように、
初期状態の梁の微小なスライスを考える。
この微小なスライスが梁の変形後、
上の方は縮んで、図心位置($y=0$)は伸び縮みせず、
下の方は伸びてバームクーヘン状になったものとする。
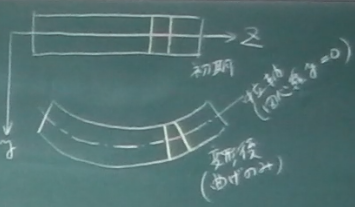
このバームクーヘンを拡大したものを描き直す。
 ベルヌーイ・オイラーの仮定により、
断面は上面や図心線や下面と直交しているとする。
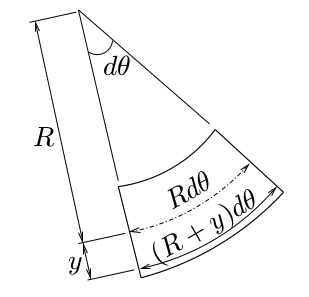
このバームクーヘンの図心線の曲率半径を$R$とし、
その中心角を$d\theta$とする。
バームクーヘンの
図心位置($y=0$)は,変形前から伸び縮みしておらず
$Rd\theta$の長さなのに対して,
図心位置から下に$y$下がった位置では,
伸びて$(R+y)d\theta$の長さになっている。
つまり,高さ方向の位置$y$での直ひずみは,
変形前の微小部分の長さに対する変形後の伸びの比率だから次式で表される。
ベルヌーイ・オイラーの仮定により、
断面は上面や図心線や下面と直交しているとする。
このバームクーヘンの図心線の曲率半径を$R$とし、
その中心角を$d\theta$とする。
バームクーヘンの
図心位置($y=0$)は,変形前から伸び縮みしておらず
$Rd\theta$の長さなのに対して,
図心位置から下に$y$下がった位置では,
伸びて$(R+y)d\theta$の長さになっている。
つまり,高さ方向の位置$y$での直ひずみは,
変形前の微小部分の長さに対する変形後の伸びの比率だから次式で表される。
$$\varepsilon_{zz}^{曲げ}(y,z)=\frac{(R+y)d\theta-Rd\theta}{Rd\theta}=\frac{y}{R}$$
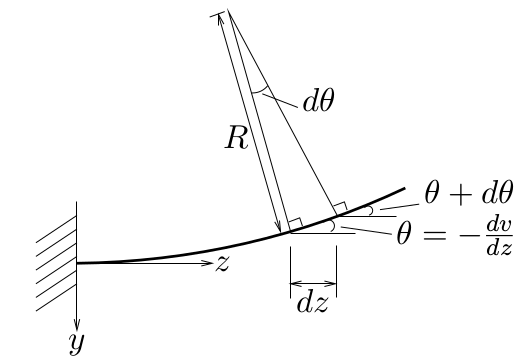 さて,曲率半径$R$と微小な角度$d\theta$, そして
この微小な部分の$z$方向の微小長さ$dz$には,
右の図のように,
近似的に$dz=Rd\theta$のような関係があるから,
${\displaystyle \frac{1}{R}=\frac{d\theta}{dz}}$と変形できる。
また,
梁のたわみ$v(z)$が,
$z$の正方向の増加に対して,$y$の負方向に増加する傾きを
${\displaystyle \theta=-\frac{dv}{dz}}$で表すと,
$d\theta$は,$z$から$dz$離れたところで梁がどれだけその傾きを増加させたかを
表している。
これらの関係を用いると,
${\displaystyle \frac{1}{R}=-\frac{d^{2}v(z)}{dz^{2}}}$となり,ひずみは
次式のように表される。
さて,曲率半径$R$と微小な角度$d\theta$, そして
この微小な部分の$z$方向の微小長さ$dz$には,
右の図のように,
近似的に$dz=Rd\theta$のような関係があるから,
${\displaystyle \frac{1}{R}=\frac{d\theta}{dz}}$と変形できる。
また,
梁のたわみ$v(z)$が,
$z$の正方向の増加に対して,$y$の負方向に増加する傾きを
${\displaystyle \theta=-\frac{dv}{dz}}$で表すと,
$d\theta$は,$z$から$dz$離れたところで梁がどれだけその傾きを増加させたかを
表している。
これらの関係を用いると,
${\displaystyle \frac{1}{R}=-\frac{d^{2}v(z)}{dz^{2}}}$となり,ひずみは
次式のように表される。
$$\varepsilon_{zz}^{曲げ}(y,z)=-y\frac{d^{2}v(z)}{dz^{2}}=-y\,v''(z)$$
${\displaystyle \frac{1}{R}=-v''(z)}$は, 曲率を表しており,ひずみ$\varepsilon_{zz}^{曲げ}(y,z)$は,ある$z$点の断面では高さ$y$方向に対して, 曲率に比例する線形分布をしていることがわかる。
さて、 初等梁に発生する唯一の直ひずみ$\varepsilon_{zz}(y,z)$を 一様な伸び成分と曲げ成分とに分解して、 それぞれを図心変位$w(z)$や$v(z)$の微分を用いて表すことができた。 これらを足し算すると、以下のように表せる。
$\varepsilon_{zz}(y,z)=\varepsilon_{zz}^{のび}(y,z)+\varepsilon_{zz}^{曲げ}(y,z)$
つまり、
$\varepsilon_{zz}(y,z)=w'(z)-y\,v''(z)$
この(梁限定の)直ひずみの 伸び成分$\varepsilon_{zz}^{のび}(y,z)=w'(z)$のことを「のびひずみ」や「軸ひずみ」と 言ったり、 曲げ成分 $\varepsilon_{zz}^{曲げ}(y,z)=-y\,v''(z)$ のことを「曲げひずみ」と言ったりする習慣(特に後者)もあるかもしれない。 しかし、 これらは、あくまで梁の直ひずみの のび成分と曲げ成分であって、 一般的な物体の 直ひずみと せん断ひずみという区別の他に 「曲げひずみ」があるわけではないので混乱しないように。