| 日付 | 時間帯 | 作業時間(hr) | 内容 | 立会 |
| 4/14 | 15:00-16:00 | 1 | カレンダー作成・タイピング練習(2分51秒) | |
| 4/15 | 13:30-16:00 | 2.5 | 英文訳・タイピング練習(2分42秒) | |
| 4/16 | 14:30-16:00 | 1.5 | 英文訳・タイピング練習(2分10秒) | |
| 4/20 | 13:30-14:30 | 1 | 英文訳・タイピング練習(2分4秒) | |
| 4/21 | 16:30-19:00 | 2.5 | 英文訳・タイピング練習(1分53秒) | |
| 4/24 | 12:30-16:00 | 3.5 | Fortran・英文訳・タイピング練習(2分0秒) | |
| 5/7 | 15:00-16:00 | 1 | Fortran | |
| 5/8 | 14:00-16:30 | 2.5 | Fortran | |
| 5/10 | 15:00-16:00 | 1 | Fortran | |
| 5/12 | 15:00-19:00 | 4 | Fortran・英文訳 | |
| 5/18 | 16:00-18:00 | 2 | 先行研究調査 | |
| 5/20 | 15:00-16:30 | 1.5 | 先行研究調査 | |
| 5/25 | 16:00-20:30(-60) | 3.5 | Salome | |
| 5/26 | 15:00-19:00(-90) | 2.5 | Salome | |
| 5/27 | 11:30-16:00(-30) | 4 | Salome・先行研究調査 | |
| 6/5 | 12:00-17:00 | 5 | Salome | |
| 6/10 | 12:00-16:00 | 4 | Salome | |
| 6/11 | 13:00-20:00 | 7 | Salome・英文訳 | |
| 6/15 | 13:00-19:00(-120) | 4 | Salome | |
| 6/16 | 14:00-20:00 | 6 | Salome | |
| 6/17 | 15:00-17:00 | 2 | Salome | |
| 6/18 | 13:00-20:00 | 7 | Salome・格子桁理論の学習 | |
| 6/21 | 10:00-15:00 | 5 | 格子桁理論の学習 | |
| 6/22 | 16:00-18:00 | 2 | 格子桁理論の学習 | |
| 6/23 | 17:30-20:00 | 2.5 | Salome | |
| 6/25 | 14:00-20:00 | 6 | Salome | |
| 6/26 | 13:00-20:00 | 7 | Salome | |
| 6/27 | 14:00-17:00 | 3 | Salome | |
| 6/29 | 17:00-20:00 | 3 | Salome | |
| 7/1 | 14:00-17:30 | 3.5 | Salome | |
| 7/2 | 16:30-18:00 | 1.5 | Salome・英文訳 | |
| 7/6 | 14:00-19:00 | 5 | Salome | |
| 7/7 | 14:30-17:30 | 3 | Salome | |
| 7/9 | 13:00-16:00 | 3 | Salome | |
| 7/10 | 15:00-17:00 | 2 | Salome | |
| 7/11 | 14:00-15:30 | 1.5 | Salome | |
| 7/13 | 16:00-18:00 | 2 | Salome | |
| 7/14 | 15:00-19:00 | 4 | Salome・英文訳 | |
| 7/16 | 14:00-19:00(-120) | 3 | Salome | |
| 7/23 | 14:00-17:00 | 3 | Salome | |
| 8/3 | 16:00-18:00 | 2 | Salome | |
| 8/26 | 14:30-16:00 | 1.5 | Salome | |
| 9/21 | 14:00-17:00 | 3 | Salome | |
| 9/24 | 18:00-25:00 | 7 | Salome | |
| 9/28 | 9:00-24:00 | 15 | 中間発表準備 | |
| 9/29 | 9:00-12:00 | 3 | 中間発表準備 | |
| 10/1 | 2:00-9:00 | 7 | Salome | |
| 10/5 | 13:00-18:00 | 5 | Salome | |
| 10/9 | 2:00-9:00 | 7 | Salome | |
| 10/16 | 2:00-9:00 | 7 | Salome | |
| 10/19 | 13:00-17:00 | 4 | Salome | |
| 10/20 | 12:00-15:00 | 3 | Salome | |
| 10/21 | 15:00-17:00 | 2 | Salome | |
| 10/23 | 4:00-6:00 | 2 | Salome | |
| 10/26 | 13:00-16:00 | 3 | tex | |
| 10/27 | 2:00-9:00 | 7 | tex | |
| 10/28 | 2:00-9:00 | 7 | tex | |
| 10/29 | 2:00-9:00 | 7 | tex | |
| 11/5 | 5:00-10:00 | 5 | tex | |
| 11/9 | 18:00-20:00 | 2 | 調査研究 | |
| 11/12 | 12:00-16:00 | 4 | 調査研究 | |
| 11/17 | 12:00-16:30 | 4.5 | tex | |
| 11/20 | 2:00-5:00 | 3 | Salome | |
| 12/2 | 11:00-17:00(-120) | 4 | Salome | |
| 12/4 | 10:30-13:00 | 2.5 | Salome | |
| 12/10 | 11:00-17:00 | 6 | Salome | |
| 12/15 | 14:00-25:00 | 13 | Salome | |
| 12/16 | 11:30-20:30 | 10 | Salome | |
| 12/17 | 12:00-17:00(-60) | 4 | Salome | |
| 12/20 | 13:00-18:00 | 5 | Salome・tex | |
| 12/22 | 6:00-10:00 | 4 | tex | |
| 12/25 | 13:00-15:00 | 2 | 休みに向けて整理等 | |
| 1/8 | 15:00-17:00 | 2 | Salome | |
| 1/13 | 17:00-23:00 | 6 | Salome | |
| 1/14 | 17:00-23:00 | 6 | Salome | |
| 1/18 | 12:00-16:00 | 4 | Salome | |
| 1/20 | 12:00-16:00 | 4 | Salome | |
| 1/21 | 9:00-16:00 | 7 | Salome | |
| 1/22 | 1:00-16:00 | 15 | Salome | |
| 1/23 | 14:00-18:00 | 4 | Salome・tex | |
| 1/25 | 2:00-9:00 | 7 | tex | |
| 1/25 | 20:00-25:00 | 5 | tex | |
| 1/26 | 0:00-17:00 | 17 | tex | |
| 1/27 | 2:00-10:00 | 8 | tex・スライド | |
| 1/28 | 2:00-15:00 | 13 | tex・スライド | |
| 1/29 | 10:00-14:00 | 4 | スライド | |
| 1/30 | 2:00-9:00 | 7 | スライド | |
| 1/31 | 2:00-9:00 | 7 | スライド | |
| 2/1 | 11:00-18:00 | 7 | スライド | |
| 合計時間 | 413.5 |

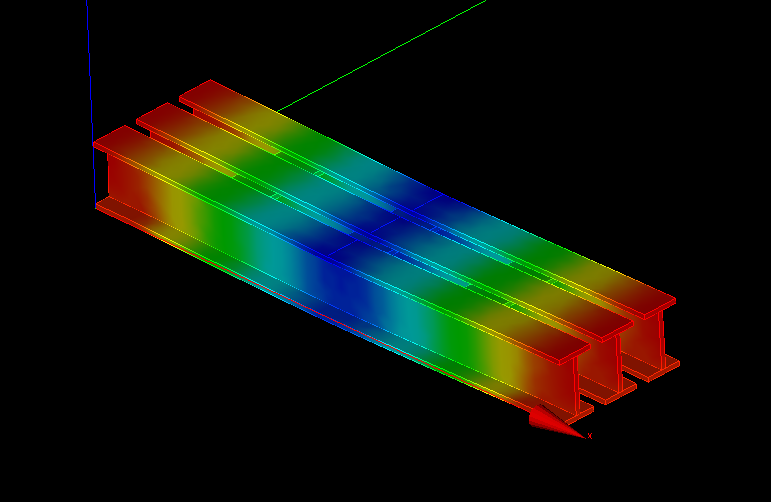
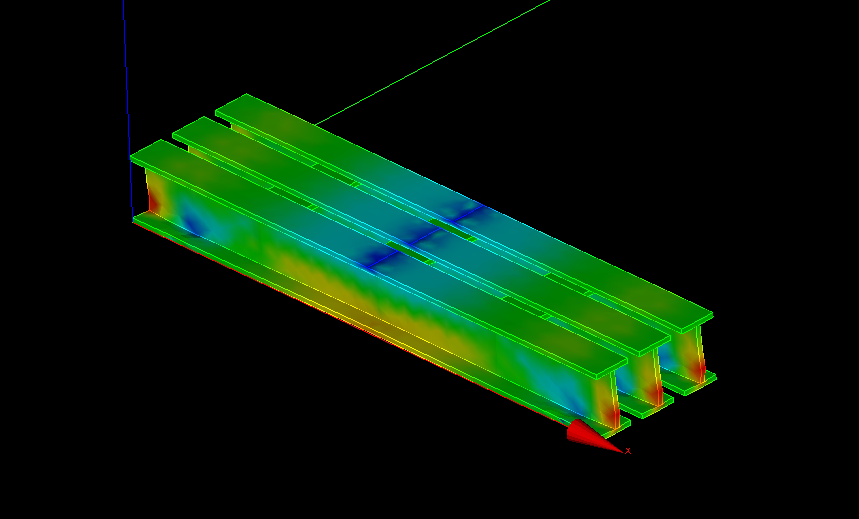
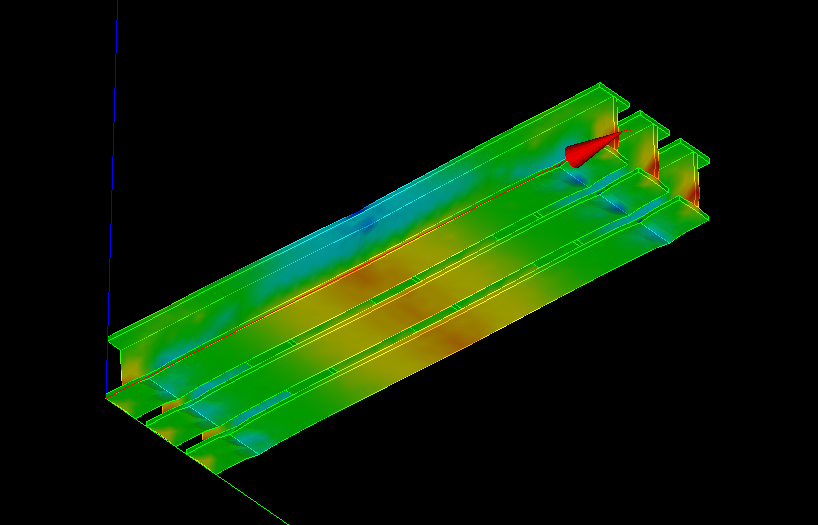
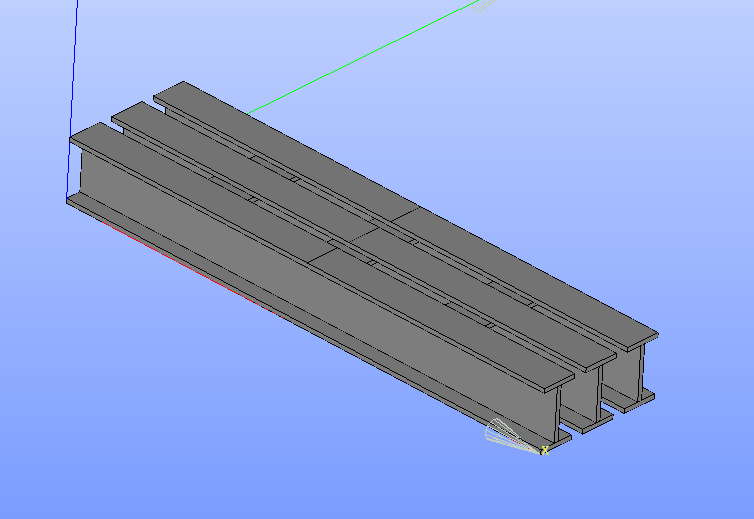
CHAR=AFFE_CHAR_MECA(MODELE=MODE,
DDL_IMPO=(
_F(GROUP_MA='Group_2',
DX=0.0,
DY=0.0,
DZ=0.0,),
_F(GROUP_MA='Group_3',
DY=0.0,
DZ=0.0,),
),
FORCE_NODALE=(
_F(GROUP_NO='Group_1',
FZ=-10000.0,),
),
);

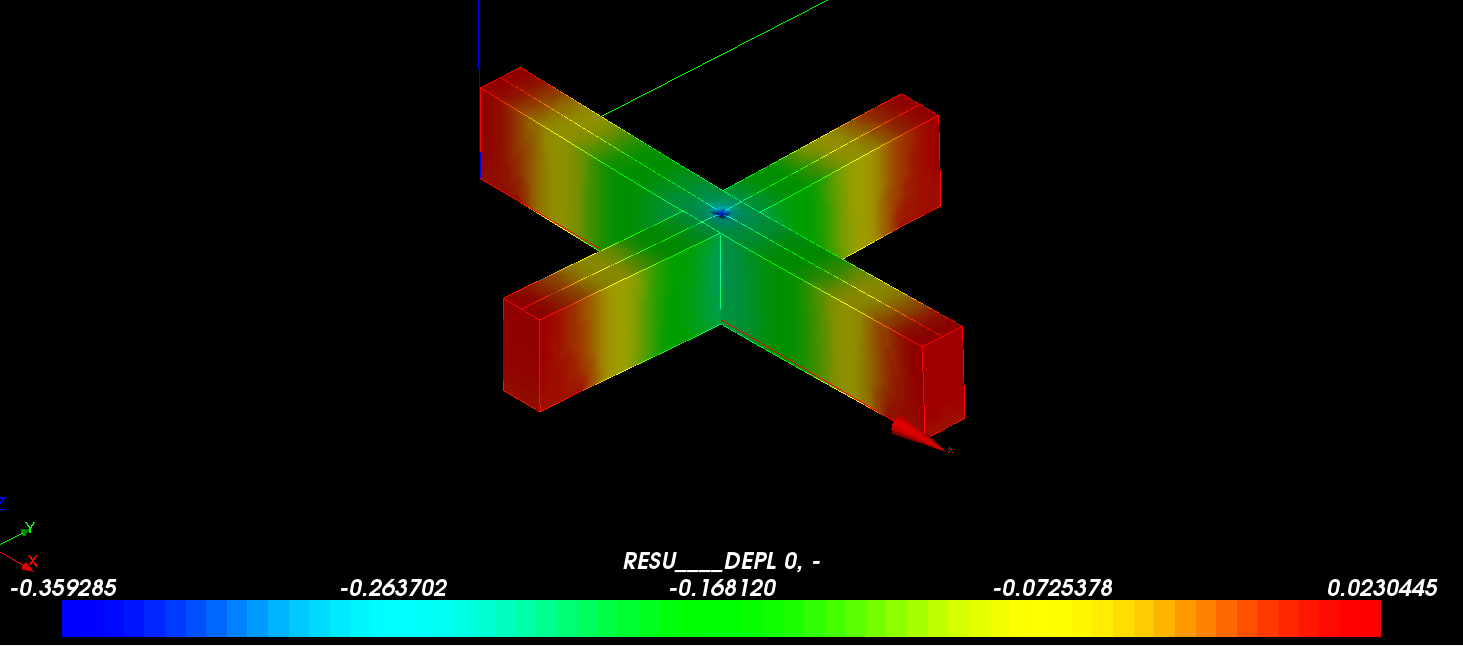
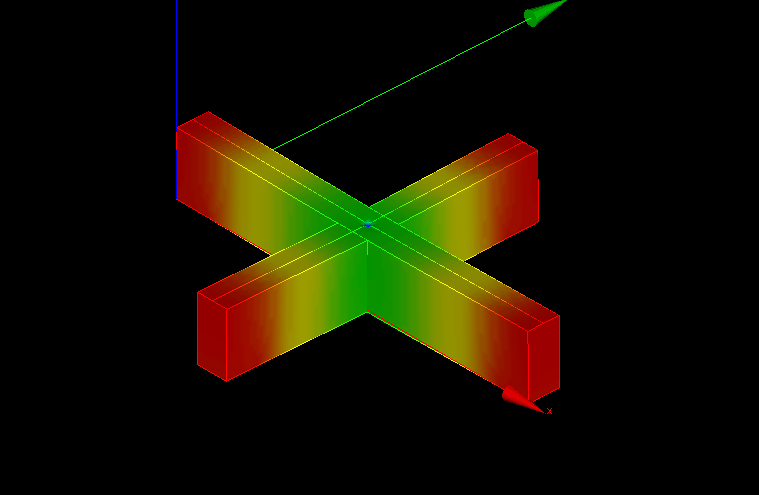
MAIL=MODI_MAILLAGE(reuse=MAIL,
MAILLAGE=MAIL,
ORIE_PEAU_3D=_F(GROUP_MA=('Group_3',),),
);
.commファイルで、この部分を削除すると、正常に解析できるようになる。理由は不明・・・
| x(mm) | y(mm) | z(mm) | スパンl(mm) | 荷重P(N/mm) | ヤング率E(GPa) | ポアソン比ν | Length | Volumes | 解析結果のたわみδ(mm) | (1)式のたわみδtimo(mm) | 相対誤差(%) |
| 120 | 10 | 20 | 100 | 100 | 2.84 | 0.313 | 1.5 | 47822 | 1.2910 | 1.2390 | 4.20 |
| 150 | 10 | 20 | 130 | 100 | 2.84 | 0.313 | 1.5 | 43521 | 2.6145 | 2.5978 | 0.64 |
| 200 | 10 | 20 | 180 | 100 | 2.84 | 0.313 | 1.5 | 104167 | 6.6266 | 6.6669 | -0.60 |
かなり相対誤差が小さく算出された。やはりモデルの断面2次の大きさから、せん断の影響を考慮しなければならなかったとわかった。
| x(mm) | y(mm) | z(mm) | スパンl(mm) | 荷重P(N/mm) | ヤング率E(GPa) | ポアソン比ν | Length | Volumes | ヒンジ拘束 | ローラー拘束 | 解析結果のたわみδ(mm) | (1)式のたわみδtimo(mm) | 相対誤差(%) |
| 200 | 10 | 20 | 180 | 100 | 2.84 | 0.313 | 1.5 | 104167 | x=0 y=0 z=0 | x≠0 y=0 z=0 | 6.6266 | 6.6669 | -0.60 |
| 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | x=0 y≠0 z=0 | x≠0 y=0 z=0 | 6.6269 | 〃 | -0.60 |
| 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | x=0 y≠0 z=0 | x≠0 y≠0 z=0 | エラーにより測定不可 | 〃 | エラーにより測定不可 |
Conseil & Risque: Il s'agit peut etre d'un mouvement de corps rigide mal bloque. Verifiez les conditions aux limites. Si vous faites du contact,il ne faut pas que la structure ne tienne que par le contact
アドバイス、コンサルティング・リスク これはひどい剛性運動であってもよい(?) 境界条件をチェックして下さい。 接触する場合は、その構造を保持していない。要するに境界条件の設定をミスしてるようだった。 拘束線両方をy≠0にすると、計算できなくなる。
| x(mm) | y(mm) | z(mm) | スパンl(mm) | 荷重P(N/mm) | ヤング率E(GPa) | ポアソン比ν | Length | Volumes | ヒンジ拘束 | ローラー拘束 | 解析結果のたわみδ(mm) | 初等梁理論のたわみ式δr(mm) | 相対誤差$\frac{δ-δr}{δr}*100$(%) | ティモシェンコ理論のたわみ式δtimo(mm) | 相対誤差$\frac{δ-δtimo}{δtimo}*100$(%) |
| 200 | 20 | 10 | 180 | 1000 | 2.84 | 0.313 | 1.5 | 70668 | x=0 z=0 | y=0 z=0 | 23.7756 | 25.6690 | -7.38 | 25.9187 | -8.27 |
| 150 | 〃 | 〃 | 130 | 〃 | 〃 | 〃 | 〃 | 48433 | 〃 | 〃 | 9.3156 | 9.6699 | -3.66 | 9.8502 | -5.43 |
| 120 | 〃 | 〃 | 100 | 〃 | 〃 | 〃 | 〃 | 70951 | 〃 | 〃 | 4.4233 | 4.4014 | 0.498 | 4.5401 | -2.57 |
断面2次を減らすことで、相対誤差自体を減らすことはできなかったが、通常のたわみ式との相対誤差と、ティモシェンコ理論との相対誤差の差は減った。 つまり、通常のたわみ式でも実際のたわみに近づけやすいことがわかる。ただ、どれもティモシェンコ理論の方が誤差が大きくなっていた。
| x(mm) | y(mm) | z(mm) | スパンl(mm) | 荷重P(N/mm) | ヤング率E(GPa) | ポアソン比ν | Length | Volumes | ヒンジ拘束 | ローラー拘束 | 解析結果のたわみδ(mm) | 初等梁理論のたわみ式δr(mm) | 相対誤差$\frac{δ-δr}{δr}*100$(%) | ティモシェンコ理論のたわみ式δtimo(mm) | 相対誤差$\frac{δ-δtimo}{δtimo}*100$(%) |
| 200 | 20 | 12 | 180 | 1000 | 2.84 | 0.313 | 1.5 | 93718 | x=0 z=0 | y=0 z=0 | 14.3625 | 14.8548 | -3.31 | 15.0628 | -4.65 |
| 150 | 〃 | 〃 | 130 | 〃 | 〃 | 〃 | 〃 | 51318 | 〃 | 〃 | 5.5282 | 5.5960 | -1.212 | 5.7463 | -3.795 |
| 120 | 〃 | 〃 | 100 | 〃 | 〃 | 〃 | 〃 | 76260 | 〃 | 〃 | 2.6276 | 2.5471 | 3.16 | 2.6627 | -1.32 |
| x(mm) | y(mm) | z(mm) | スパンl(mm) | 荷重P(N/mm) | ヤング率E(GPa) | ポアソン比ν | Length | Volumes | ヒンジ拘束 | ローラー拘束 | 解析結果のたわみδ(mm) | 初等梁理論のたわみ式δr(mm) | 相対誤差$\frac{δ-δr}{δr}*100$(%) | ティモシェンコ理論のたわみ式δtimo(mm) | 相対誤差$\frac{δ-δtimo}{δtimo}*100$(%) |
| 200 | 20 | 8 | 180 | 1000 | 2.84 | 0.313 | 1.5 | 73381 | x=0 z=0 | y=0 z=0 | 45.8184 | 50.1348 | -8.610 | 50.4469 | -9.175 |
| 150 | 〃 | 〃 | 130 | 〃 | 〃 | 〃 | 〃 | 43667 | 〃 | 〃 | 7.0329 | 18.8865 | -62.762 | 19.1119 | -63.201 |
| 120 | 〃 | 〃 | 100 | 〃 | 〃 | 〃 | 〃 | 57711 | 〃 | 〃 | 8.3199 | 8.5965 | -3.218 | 8.7699 | -5.13 |
Exception utilisateur levee mais pas interceptee. Les bases sont fermees. Type de l'exception:error Vous avez demande l'affectation d'un modele sur un GROUP_MA,or le maillage MAIL n'en contient ancun. L'affectation du modele n'est donc pas possible.
ユーザー例外堤防が、キャッチされません(?) 塩基は閉じられています(?) 例外の種類:エラー あなたが要求したGROUP_MAの要素分割、MAIL金メッシュ(?)はどれも含まれていません。 要素分割が不可能です。Meshの切り方に問題があると思われる。
| x(mm) | y(mm) | z(mm) | スパンl(mm) | 荷重P(N/mm) | ヤング率E(GPa) | ポアソン比ν | Length | Volumes | ヒンジ拘束 | ローラー拘束 | 解析結果のたわみδ(mm) | 初等梁理論のたわみ式δr(mm) | 相対誤差$\frac{δ-δr}{δr}*100$(%) | ティモシェンコ理論のたわみ式δtimo(mm) | 相対誤差$\frac{δ-δtimo}{δtimo}*100$(%) | |
| 1 | 200 | 20 | 10 | 180 | 1000 | 2.84 | 0.313 | 1.0 | 198910 | x=0 z=0 | y=0 z=0 | 25.2916 | 25.6690 | -1.47 | 25.9187 | -2.42 |
| 2 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 0.9 | 205485 | 〃 | 〃 | 25.2902 | 〃 | -1.48 | 〃 | -2.42 |
| 3 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 0.8 | 230654 | 〃 | 〃 | 25.2929 | 〃 | -1.47 | 〃 | -2.41 |
| 4 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 0.7 | 521953 | 〃 | 〃 | エラー | 〃 | ー | 〃 | ー |
| 5 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 0.6 | 569705 | 〃 | 〃 | エラー | 〃 | ー | 〃 | ー |
| 6 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 〃 | 0.5 | 1273818 | 〃 | 〃 | エラー | 〃 | ー | 〃 | ー |
Exception utilisateur levee mais pas interceptee. Les bases sont fermees. Type de l'exception : error Erreur lors de l'allocation dynamique. Il n'a pas été possible d'allouer une zone mémoire de longueur 52 Mo, on dépasse la limite maximum fixée à 255 Mo et on occupe déjà 208 Mo. La dernière opération de libération mémoire a permis de récupérer 0 Mo.
ユーザー例外堤防が、キャッチされません(?) 塩基は閉じられています(?) 例外の種類:エラー ↑この上3行はいつも出てくるから、決まり文句(?) 動的割り当て中にエラーが発生しました。これは、割り当てることができませんでした。 52メガバイトの記憶領域の長さは、上限を超えた。 255メガバイトに設定し、 208メガバイトはすでに持っています。 メモリを解放する最後の操作は0メガバイトを回復する助け。要素数は多すぎてエラーが起きたと考えられる。メモリ容量の問題だと思う。
| Length | Volumes | 解析結果のたわみδ(mm) | 初等梁理論のたわみ式δr(mm) | 相対誤差$\frac{δ-δr}{δr}*100$(%) | ティモシェンコ理論のたわみ式δtimo(mm) | 相対誤差$\frac{δ-δtimo}{δtimo}*100$(%) |
| 0.700 | 521953 | エラー | 25.6690 | ー | 25.9187 | ー |
| 0.710 | 520928 | エラー | 〃 | ー | 〃 | ー |
| 0.720 | 404937 | エラー | 〃 | ー | 〃 | ー |
| 0.730 | 383885 | エラー | 〃 | ー | 〃 | ー |
| 0.740 | 275692 | エラー | 〃 | ー | 〃 | ー |
| 0.741 | 262228 | 25.3226 | 〃 | -1.35 | 〃 | -2.30 |
| 0.750 | 254331 | 25.3193 | 〃 | -1.36 | 〃 | -2.31 |
Compliation impossible; file 0804.comm,line38. Syntax error keyword argument repeated
不可能なコンパイル。 0804.commファイルの、38行目。 構文エラーのキーワード引数を繰り返します
CHAR=AFFE_CHAR_MECA(MODELE=MODE,
DDL_IMPO=(
_F(GROUP_MA='fix1',
DX=0.0,
DY=0.0,
DZ=0.0,),
_F(GROUP_MA='fix2',
DX=0.0,
DY=0.0,
DZ=0.0,),
_F(GROUP_MA='fix3',
DX=0.0,
DZ=0.0,),
_F(GROUP_MA='fix4',
DX=0.0,
DZ=0.0,),
),
FORCE_ARETE=(
_F(GROUP_MA='load1',
FZ=-5.0,),
),
→38行目 FORCE_ARETE=(
_F(GROUP_MA='load2',
FZ=-5.0,),
),
);
CHAR=AFFE_CHAR_MECA(MODELE=MODE,
DDL_IMPO=(
_F(GROUP_MA='fix1',
DX=0.0,
DY=0.0,
DZ=0.0,),
_F(GROUP_MA='fix2',
DX=0.0,
DY=0.0,
DZ=0.0,),
_F(GROUP_MA='fix3',
DX=0.0,
DZ=0.0,),
_F(GROUP_MA='fix4',
DX=0.0,
DZ=0.0,),
),
FORCE_ARETE=(
_F(GROUP_MA='load1',
FZ=-5.0,),
→ここをこうした _F(GROUP_MA='load2',
FZ=-5.0,),
),
);
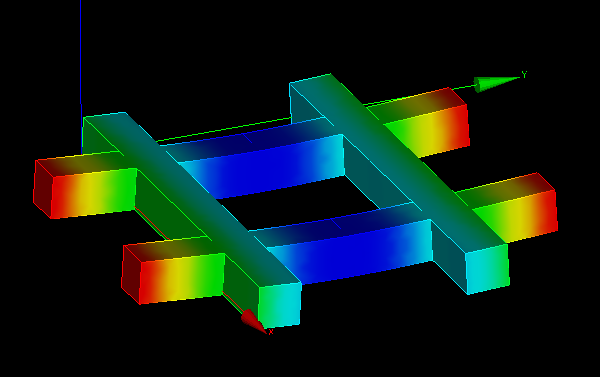
| 体積(mm^3) | ヤング率(N/mm^2) | ポアソン比 | 荷重(N/mm) | たわみ(mm) | 剛性 | 比剛性 | |
| 基本形 | 27000000 | 205000 | 0.3 | 1000 | -0.00124737 | 4.83×10^13 | 1789068 |
| 補剛材 | 27003680 | 〃 | 〃 | 〃 | -0.00194102 | 2.95×10^13 | 1092444 |
結果的に補剛材を取り付けたほうが下方向へのたわみが大きくなった。

ただし、K=6EI/a$^3$k
| 分子 | 分子 | 分母 | ||
| ωK | K | |||
| X11-1= | X13= | -1 | N1 | |
| X12= | +2 | N1 | ||
| X21= | X23= | +2 | N1 | |
| X22-1= | -4 | N1 |
Xの左側は載荷、右側は反力がどの主桁を示しているかを表す。 つまり以下のようになる。
主桁のねじり剛度のない格子桁に対するLeonhardtの方法で解く
例)主桁数m、主桁1との格子点にP=1が作用(j=1)
格子力は
例えば右側の主桁に載荷した場合、左側の主桁は上に引っ張られる(ばねで言うと伸びてる状態)。よって反力としては下向きになる。3つ目がマイナス方向(上方向)になるのも理解できる。
コア材料は、軽量、高剛性、高強度のため航空、宇宙機分野で活用されている。加工技術の発展により自動車、鉄道、建築にも利用が広がっている。防音、遮音、断熱性、デザイン性などの優れた機能がある反面、高価格であることから建材への利用を妨げている要因になっている。市販の軽量コアのほとんどは、アルミ箔、紙、プラスチックなどを接着剤で成型しており、加工が容易であるが、コア構造の強度は接着剤の特性に大きく依存し、高温にさらされる部品には活用できない。また強化できるのは一方向位のみの剛性であり、高度な構造的要請には答えられない。 最も主流なハニカムコアは軍用機に搭載されて以来、接着剤の改良などにより様々な研究が行われた。その一方で、ハニカムコア以外のコア構造の研究はあまり行われておらず、ハニカム構造と競合するような新しい加工法などは未開発である。 軽量化が図れるコア構造は、高コストであることを克服すれば様々な工業品への利用が期待される。低コスト化を図るために、容易に作製できる新しいコアモデルの開発が必要である。
この形を作ってみる。
ガラス繊維で強化された熱硬化性樹脂(GFRP)
実物は少し大きすぎたので、5分の1の大きさで作成した。 体積は1,286,000mm^3で統一した。 荷重は、約100Kgがかかったとして、1025Nとなるように単位荷重を調整した。
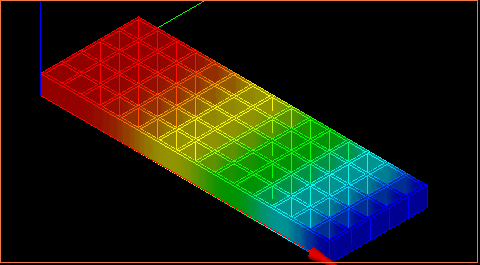
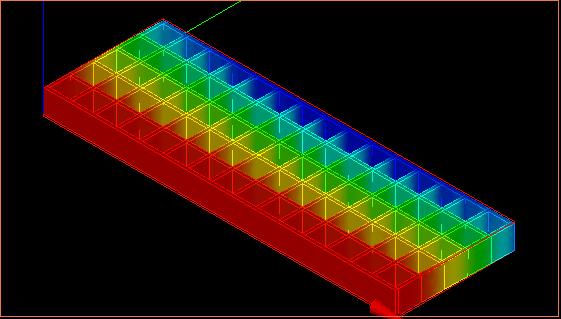
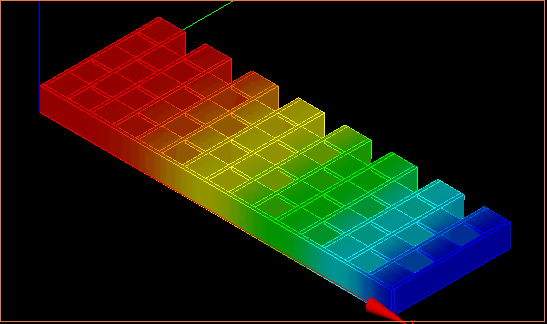
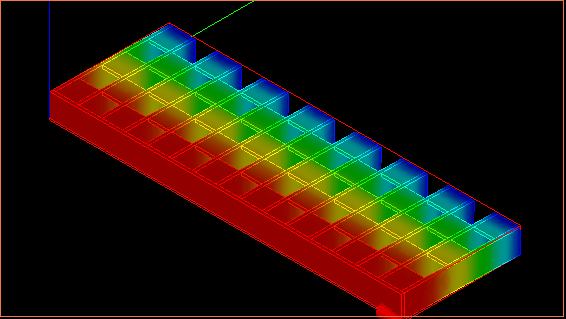
それぞれ、剛性($N・mm^2$)を一覧でまとめると以下の通り
| 短辺を拘束 | 長辺を拘束 | |
| 格子パネル |  7.65×10$^9$ 7.65×10$^9$ |  19.3×10$^9$ 19.3×10$^9$ |
| 折り紙コアパネル |  5.63×10$^9$ 5.63×10$^9$ |  32.0×10$^9$ 32.0×10$^9$ |
| ↑格子の方が強い | ↑折り紙コアの方が強い |
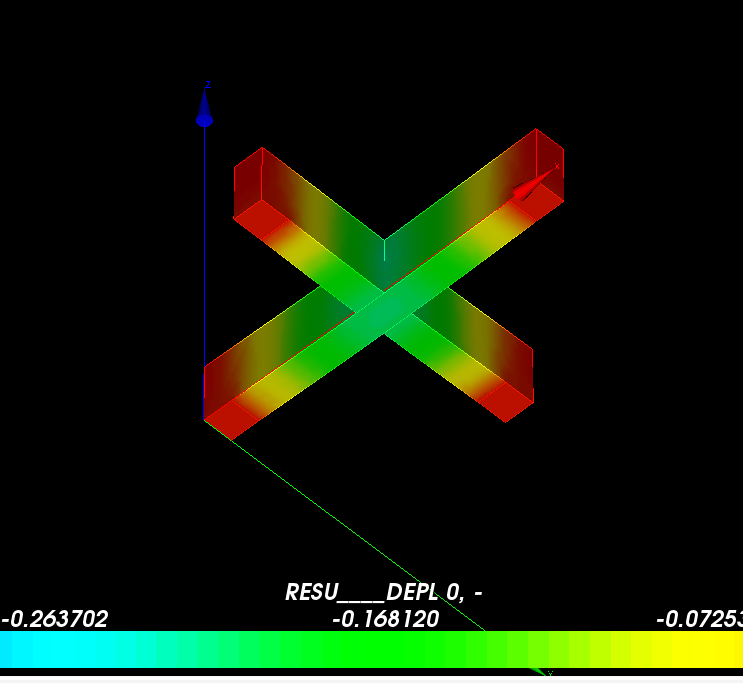
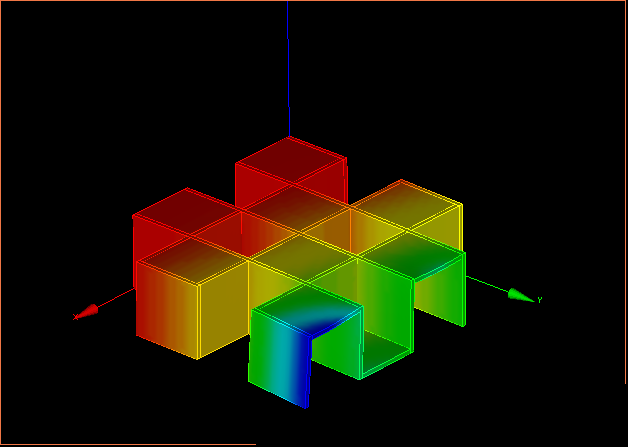 δ=-4.27244e-06〜-0.0502179mm
最大たわみは、局部的にたわんでしまっているところで、先端全体のたわみは、だいたい
δ=-0.0251068mm
δ=-4.27244e-06〜-0.0502179mm
最大たわみは、局部的にたわんでしまっているところで、先端全体のたわみは、だいたい
δ=-0.0251068mm
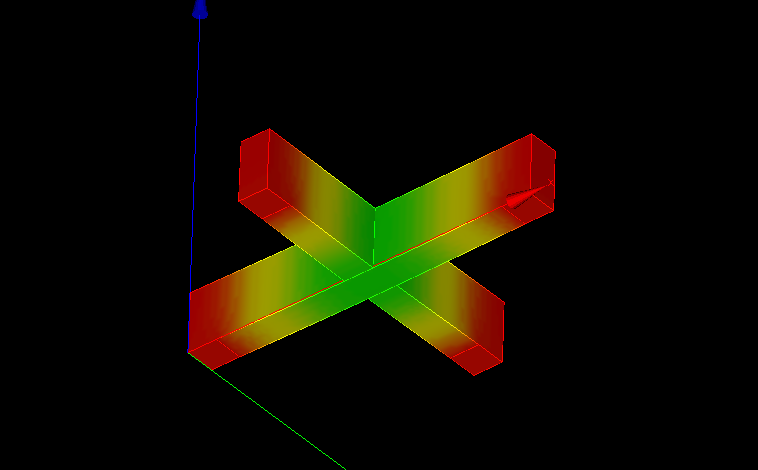
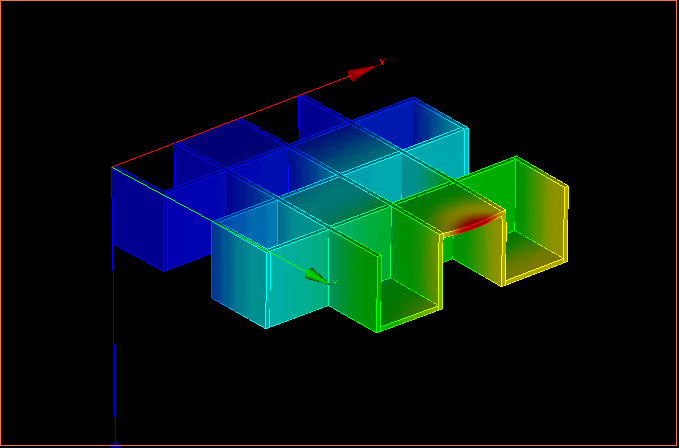 δ=4.21407e-06〜0.041586230mm
最大たわみは、局部的にたわんでしまっているところで、先端全体のたわみは、だいたい
δ=0.0207910mm
δ=4.21407e-06〜0.041586230mm
最大たわみは、局部的にたわんでしまっているところで、先端全体のたわみは、だいたい
δ=0.0207910mm
 δ=-5.50049e-06〜-0.0556089mm
最大たわみは、局部的にたわんでしまっているところで、先端全体のたわみは、だいたい
δ=-0.0278017mm
δ=-5.50049e-06〜-0.0556089mm
最大たわみは、局部的にたわんでしまっているところで、先端全体のたわみは、だいたい
δ=-0.0278017mm
 δ=5.50101e-06〜0.0551563mm
最大たわみは、局部的にたわんでしまっているところで、先端全体のたわみは、だいたい
δ=0.0275754mm
δ=5.50101e-06〜0.0551563mm
最大たわみは、局部的にたわんでしまっているところで、先端全体のたわみは、だいたい
δ=0.0275754mm
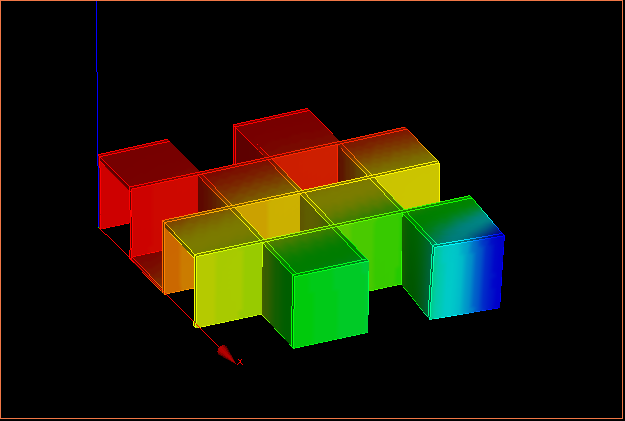
たわみ方をまとめると、
| 壁なし面を拘束・載荷 | 壁あり面を拘束・載荷 | |
| 表向き載荷 | 0.0251068mm | 0.0278017mm |
| 裏向き載荷 | 0.0207910mm | 0.0275754mm |
壁がない面を拘束=軸方向に水平な面が増えるので、曲げに対する部材が増える。 よって、壁がない面を拘束したほうが曲げには強くなったと考えられる。 また、裏向きの方が曲げには強い=上面よりも下面に壁が多いほうが強い。
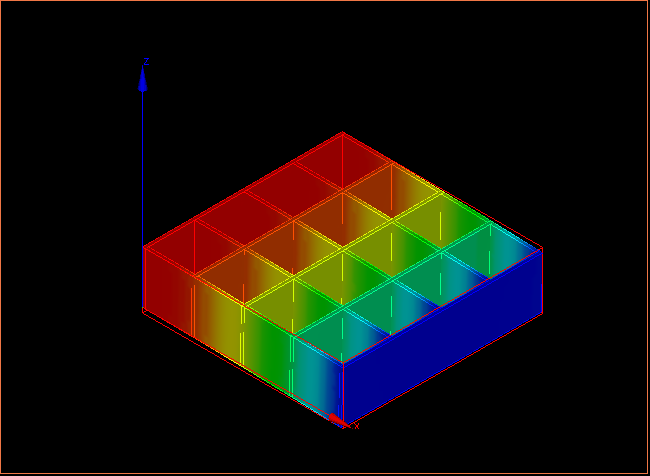 たわみは、δ=0.0321990mmであった。
折り紙コアの方が、最大たわみ(局部的なたわみだが)は大きかったが、
先端の平均的なたわみは、格子パネルにも劣らない性能を見せた。むしろ、格子パネルよりも強いのかもしれない。
たわみは、δ=0.0321990mmであった。
折り紙コアの方が、最大たわみ(局部的なたわみだが)は大きかったが、
先端の平均的なたわみは、格子パネルにも劣らない性能を見せた。むしろ、格子パネルよりも強いのかもしれない。
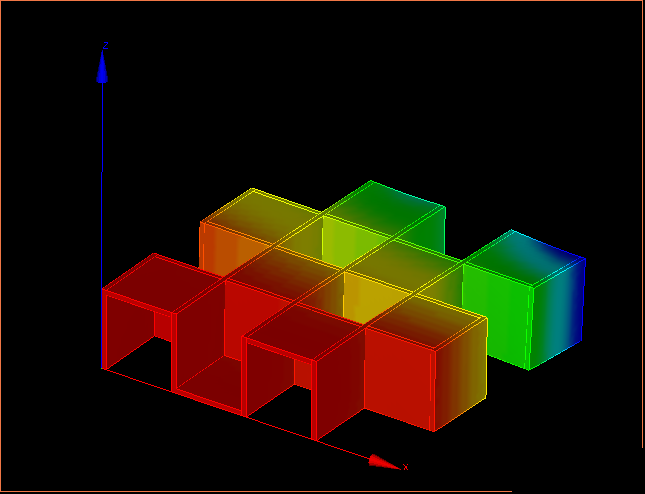
 ↑変位の様子
↑変位の様子

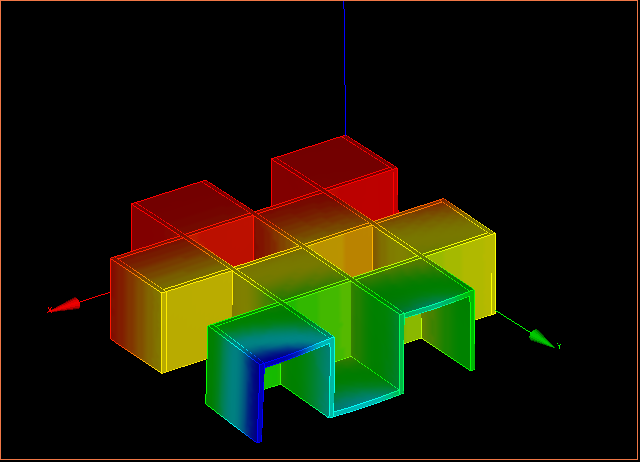
 ↑応力分布の様子
↑応力分布の様子
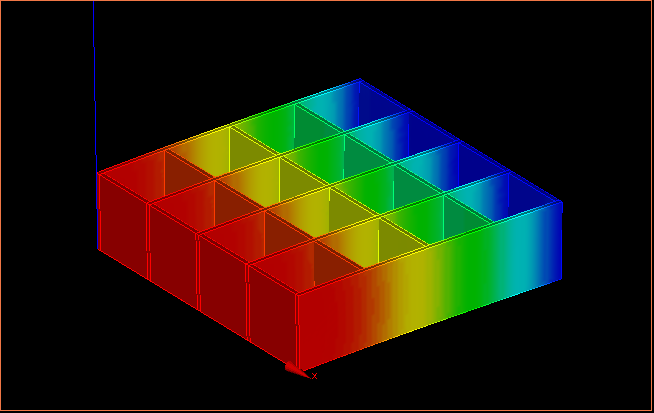
 ↑変位の様子
↑変位の様子
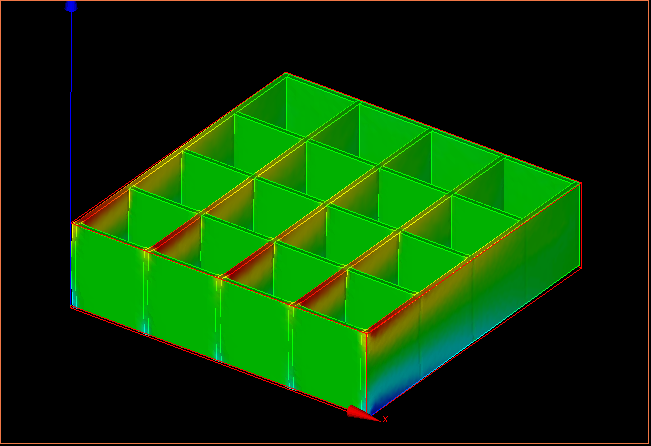
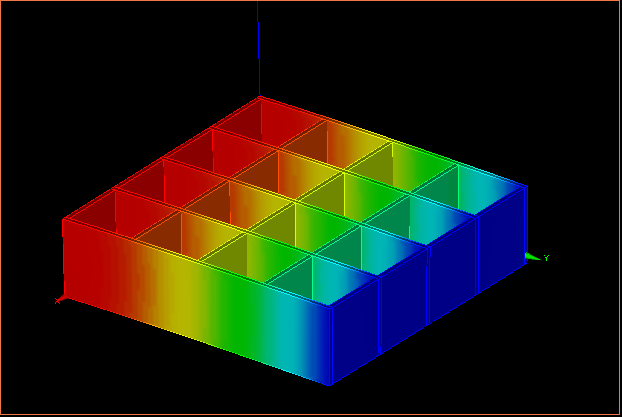
 ↑応力分布の様子
↑応力分布の様子
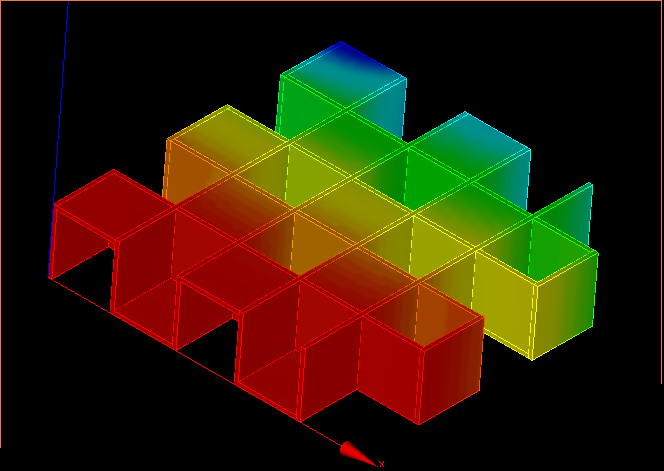
 ↑変位の様子
↑変位の様子
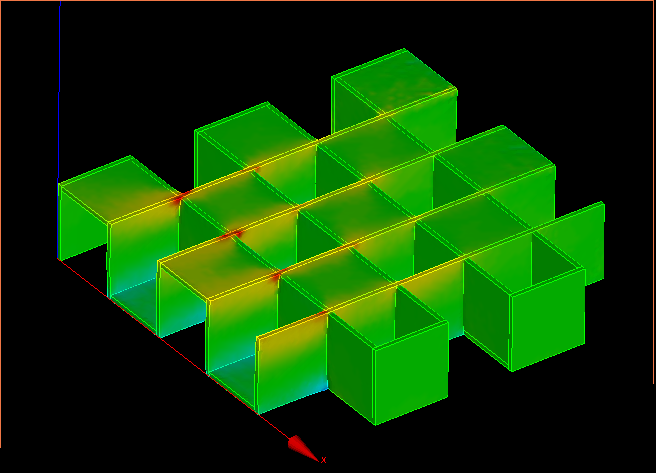
 ↑応力分布の様子
↑応力分布の様子
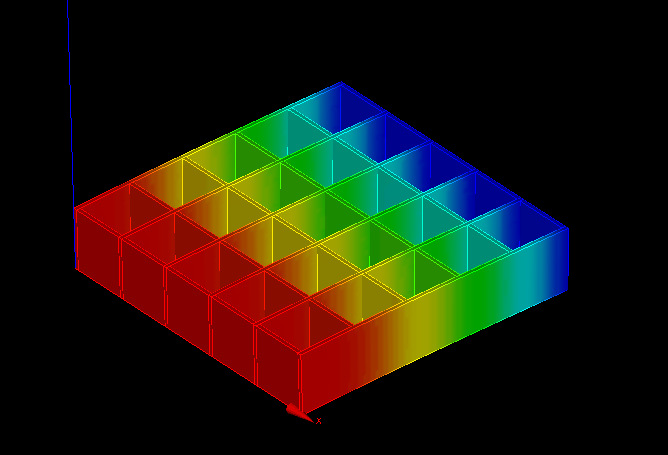
 ↑変位の様子
↑変位の様子
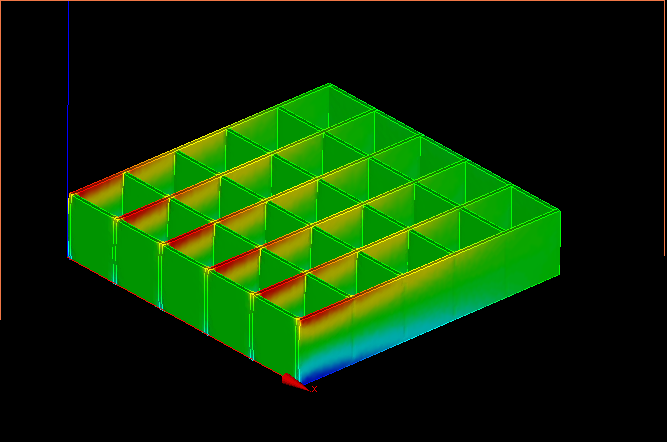
 ↑応力分布の様子
↑応力分布の様子
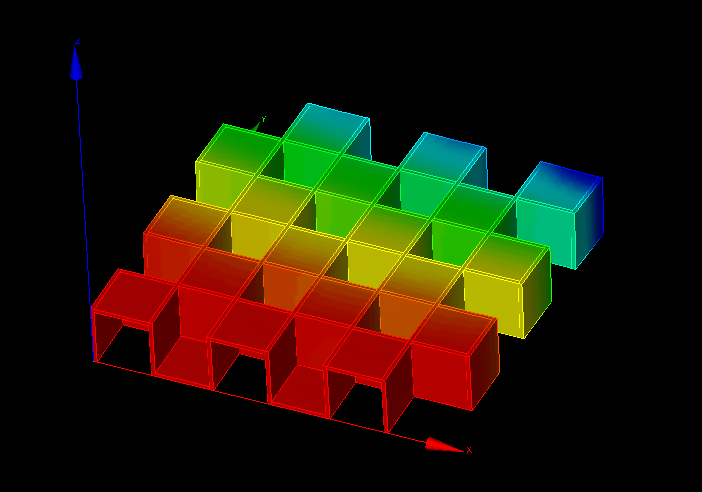
 ↑変位の様子
↑変位の様子
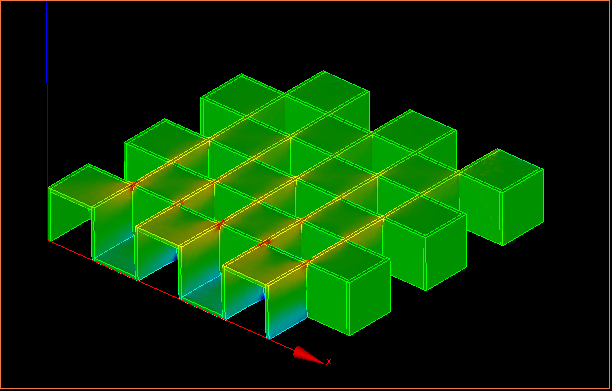
 ↑応力分布の様子
↑応力分布の様子
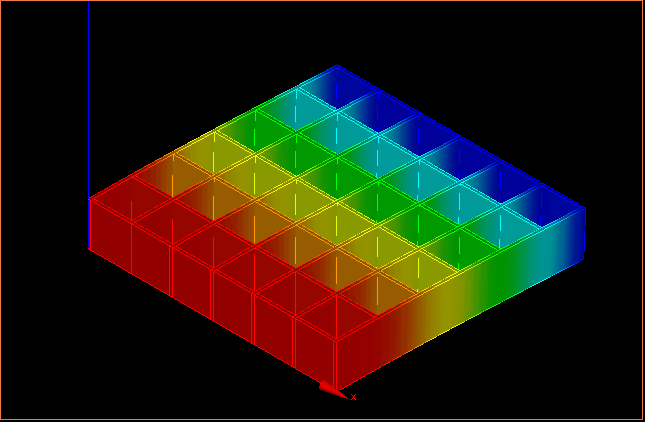
 ↑変位の様子
↑変位の様子
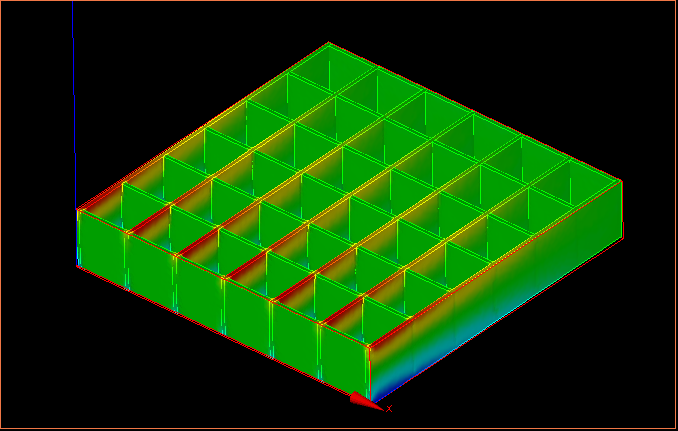
 ↑応力分布の様子
↑応力分布の様子
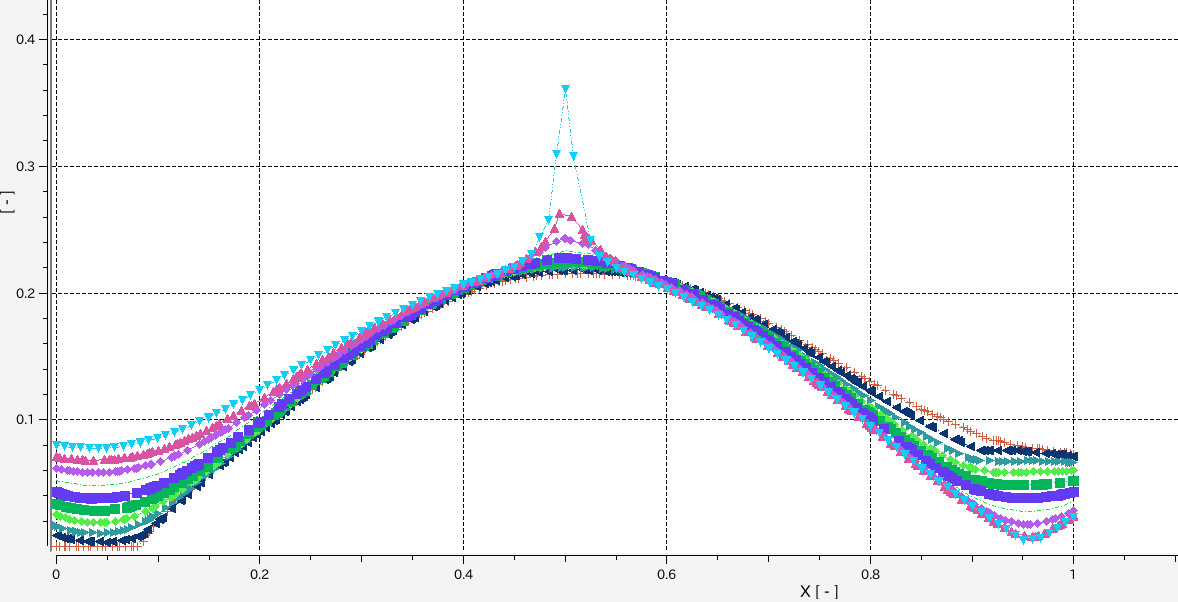
| 変位 | 体積82568mm$^3$ | 体積133384mm$^3$ | 体積196232mm$^3$ | 体積271112mm$^3$ |
| 折り紙コアー平均たわみmm | 0.0361873 | 0.0467128 | 0.0612740 | 0.0786173 |
| 折り紙コアー最大たわみmm | 0.0500088 | 0.0611417 | 0.0727009 | 0.08813738 |
| 格子ー平均たわみmm | 0.0327045 | 0.0490847 | 0.0688044 | 0.0919474 |
| 格子ー最大たわみmm | 0.0331276 | 0.0496539 | 0.0694428 | 0.0927135 |
| 剛性 | 体積82568mm$^3$ | 体積133384mm$^3$ | 体積196232mm$^3$ | 体積271112mm$^3$ |
| 折り紙コアー平均たわみを取った時の剛性 | 1.983×10$^9$ | 2.973×10$^9$ | 3.893×10$^9$ | 4.796×10$^9$ |
| 折り紙コアー最大たわみを取った時の剛性 | 1.429×10$^9$ | 2.271×10$^9$ | 3.281×10$^9$ | 4.278×10$^9$ |
| 格子ー平均たわみを取った時の剛性 | 2.181×10$^9$ | 2.858×10$^9$ | 3.541×10$^9$ | 4.222×10$^9$ |
| 格子ー最大たわみを取った時の剛性 | 2.153×10$^9$ | 2.826×10$^9$ | 3.541×10$^9$ | 4.187×10$^9$ |
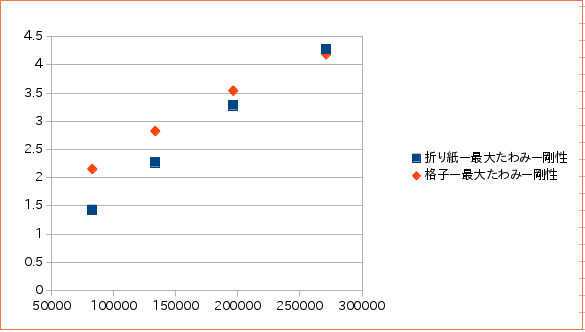 最大たわみを取って出した剛性である。
いずれも格子パネルの方が剛性が高いが、徐々に差を縮め、体積250000mm$^3$では折り紙コアパネルの方が剛性が高くなりそう。
折り紙コア構造は、上図の変位の様子からもわかるように、局部的にたわんでしまう箇所があるため、このような結果になったと思う。
最大たわみを取って出した剛性である。
いずれも格子パネルの方が剛性が高いが、徐々に差を縮め、体積250000mm$^3$では折り紙コアパネルの方が剛性が高くなりそう。
折り紙コア構造は、上図の変位の様子からもわかるように、局部的にたわんでしまう箇所があるため、このような結果になったと思う。
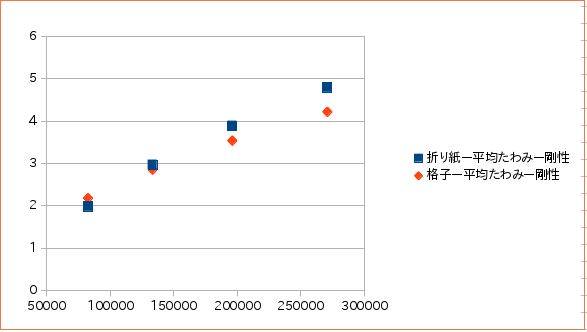 平均たわみを取って出した剛性である。
体積が大きくなるごとに、折り紙コアパネルが格子パネルを上回る結果となった。
平均たわみを取って出した剛性である。
体積が大きくなるごとに、折り紙コアパネルが格子パネルを上回る結果となった。