
| モデル | σxx | σyy | σzz |
 |  |  |  |
| 変位mm | 剛性Nmm2 | 体積mm3 | 比剛性N/mm | 比剛性$\frac{I}{lV}=\frac{pl^2}{48EδV}$ |
| 0.352094 | 3.7869e16 | 25915712685.29 | 1461224.54 | 4.97016e-4 |
| prin1 | prin2 | prin3 | vmis | |
| max | 0.215476 | |||
| roof | 0.0521302 | |||
| % | 24.19 |
| 変位mm | 剛性Nmm2 | 体積mm3 | 比剛性N/mm | 比剛性$\frac{I}{lV}=\frac{pl^2}{48EδV}$ |
| 0.347775 | 0.38339e16 | 1.1536110e11 | 332338.77 | 11.304e-4 |
| 変位mm | 剛性Nmm2 | 体積mm3 | 比剛性N/mm | 比剛性$\frac{I}{l^4}=\frac{p}{48δlE}$無次元化 |
| 0.295291 | 8.281096726e16 | 2.0776998e11 | 398570.4155 | 4.401093073e-6 |
| 変位mm | 剛性N/mm | 体積mm3 | 比剛性Nmm | 比剛性$\frac{I}{l^4}=\frac{p}{48δlE}$無次元化 |
| 5.63870 | 8.281104983e16 | 2.0776998e11 | 398570.8129 | 4.401097461e-6 |
| 変位mm | 剛性N/mm | 体積mm3 | 比剛性Nmm | 比剛性$\frac{I}{l^4}=\frac{p}{48δlE}$無次元化 |
| 0.153538 | 2.17101521e16 | 2.0776998e11 | 104491.2846 | 4.615253423 |
| σxx | σyy | σzz | σxy | σyz | σzx | |
| 引張応力(N/mm2=MPa) | 0.160461 | 0.197215 | 0.057018 | 0.015821 | 0.048863 | 0.01213 |
| 圧縮応力(N/mm2=MPa) | 0.138722 | 0.181695 | 0.082022 | 0.015245 | 0.029771 | 0.02486 |

| 変位mm | 剛性N/mm | 体積mm3 | 比剛性Nmm | 比剛性$\frac{I}{l^4}=\frac{p}{48δlE}$無次元化 |
| 0.407857 | 1.555562166e16 | 1.521024773e11 | 102270.666 | 2.233142766e-6 |
| σxx | σyy | σzz | σxy | σyz | σzx | |
| 引張(N/mm2) | 0.075899687 | 0.189337503 | 0.100353022 | 0.058967534 | 0.099104685 | 0.084347755 |
| 圧縮(N/mm2) | 0.0946863 | 0.16303043 | 0.09876461 | 0.03406855 | 0.07596203 | 0.07174582 |
| 引張(N/mm2) | 圧縮(N/mm2) |
| 88.2 | 34.3 |
| 変位mm | 剛性N/mm | 体積mm3 | 比剛性Nmm | 比剛性$\frac{I}{l^4}=\frac{p}{48δlE}$無次元化 |
| 0.568693 | 1.875751e16 | 1.4377775e11 | 130461.8922 | 1.347076869e-6 |
| 変位mm | 剛性N/mm | 体積mm3 | 比剛性Nmm | 比剛性$\frac{I}{l^4}=\frac{p}{48δlE}$無次元化 |
| 18.1297 | 2.330966814e16 | 1.4377775e11 | 162122.9164 | 1.672990978e-6 |
| 変位mm | 剛性N/mm | 体積mm3 | 比剛性Nmm | 比剛性$\frac{I}{l^4}=\frac{p}{48δlE}$無次元化 |
| 2.17046 | 0.6143091019e16 | 1.15324317680e11 | 53267.95 | 0.326e-6 |
| σxx | σyy | σzz | σxy | σyz | σzx | |
| 引張応力(MPa) | 0.274782 | 0.4491473 | 0.312142 | 0.3406998 | 0.2515137 | 0.593873 |
| 圧縮応力(MPa) | 0.653959 | 1.0457140 | 0.445910 | 0.14482 | 0.194816 | 0.217931 |
| 変位mm | 剛性Nmm2 | 体積mm3 | 比剛性N/mm | 比剛性$\frac{I}{l^4}=\frac{p}{48δlE}$無次元化 |
| 1.20312 | 1.108229714e16 | 1151202056 | 9626717.64 | 3.274393755e-4 |
| 変位mm | 剛性Nmm2 | 体積mm3 | 比剛性N/mm | 比剛性$\frac{I}{l^4}=\frac{p}{48δlE}$無次元化 |
| 0.347775 | 0.38339e16 | 115361095002 | 332338.770 | 2.037572511e-6 |
| σxx | σyy | σzz | σxy | σyz | σzx | |
| 引張(N/mm2) | 0.1408525 | 0.2104697 | 0.0885967 | 0.0310903 | 0.0464822 | 0.0206721 |
| 圧縮(N/mm2) | 0.152174 | 0.221781 | 0.08482 | 0.020372 | 0.053523 | 0.042516 |
| 引張(N/mm2) | 圧縮(N/mm2) |
| 88.2 | 34.3 |
| 変位mm | 剛性Nmm2 | 体積mm3 | 比剛性N/mm | 比剛性$\frac{I}{l^4}=\frac{p}{48δlE}$無次元化 |
| 6.95551 | 3.833890925e16 | 115361095002 | 332338.2918 | 2.037569582e-6 |
| 変位mm | 剛性Nmm2 | 体積mm3 | 比剛性N/mm | 比剛性$\frac{I}{l^4}=\frac{p}{48δlE}$無次元化 |
| 0.218204 | 6.1104898e16 | 291104834900 | 209906 | 7.13968876e-4 |
| model | 変位mm | 剛性Nmm2 | 体積mm3 | 比剛性N/mm | 比剛性$\frac{I}{l^4}=\frac{p}{48δlE}$ | $\frac{I}{lV}=\frac{pl^2}{48EδV}$ |
| 阿蘇望橋 | 0.153538 | 2.17101521e16 | 2.0776998e11 | 104491.2846 | 4.615253423e-6 | 14.2165013 |
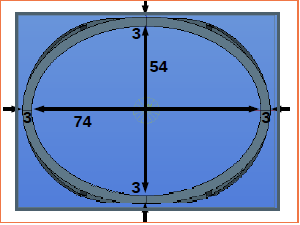
| 楕円 | 2.17046 | 0.614309e16 | 1.1532432e11 | 53267.95 | 0.326e-6 | 1.812e-4 |
| 五角形 | 0.347775 | 0.38339e16 | 1.1536110e11 | 332338.77 | 2.038e-6 | 11.304e-4 |
| 楕円(柱下) | 1.20312 | 1.108229714e16 | 1151202056 | 9626717.64 | 0.58898e-7 | 3.27439e-4 |
| 足アーチ | 0.218204 | 6.1104898e16 | 291104834900 | 209906 | 7.13968876e-4 |
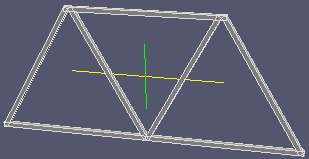
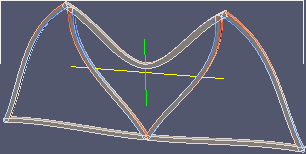
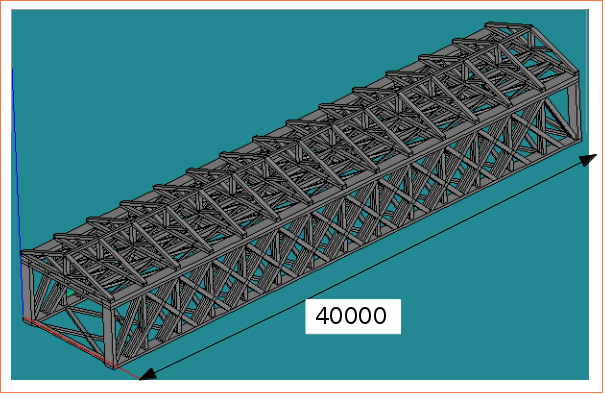
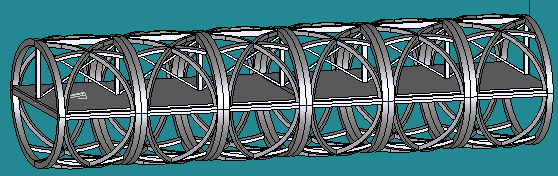
| 阿蘇望橋モデル | 五六角形複合モデル | 楕円モデル | 楕円モデル(柱下) |
 | 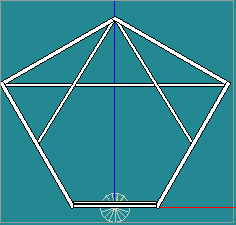 | 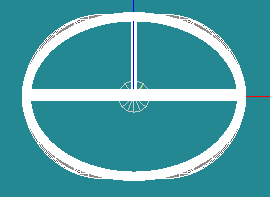 | 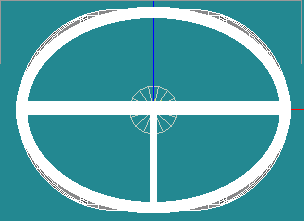 |
| prin1 | prin2 | prin3 | vmis | |
| max | 0.188068 | 0.158503 | 0.20111 | 0.188454 |
| roof | 0.0167568588 | 4.3444e-6 | 0.000508593 | |
| % | 8.91 | 0.0027 | 0.253 |
| prin1 | prin2 | prin3 | vmis | |
| max | 0.238 | 0.149112 | 0.225928 | 0.218978 |
| roof | 0.0645548 | 0.00230906 | -0.000918028 | |
| % | 27.12 | 1.55 | 0.41 |
| prin1 | prin2 | prin3 | vmis | |
| max | 1.20726 | 0.692081 | 0.912063 | 0.192435 |
| roof | 0.121103 | 0.0216219 | 0.00186322 | |
| % | 10.03 | 3.124 | 0.204 |
| prin1 | prin2 | prin3 | vmis | |
| max | 0.340681 | |||
| roof | 0.0526328 | |||
| % | 15.44929127 |
| prin1 | prin2 | prin3 | vmis | |
| max | 0.370553 | |||
| roof | 0.00573577 | |||
| % | 1.54789 |
| 1/1 | 1/4(w=2.5N/mm) | 1/4(w=5.0N/mm) | 1/4(w=0.1N/mm2) | xy=0なし | 理論式 | |
| たわみmm(aster) | 7.94168 | 4.14721 | 8.29441 | 9.087 | 8.88776 | 9.1022($\frac{pl^3}{48EI}$) |
| 相対誤差% | 12.750 | 54.437 | 8.875 | ◎0.166992595 | 2.413 | 0 |
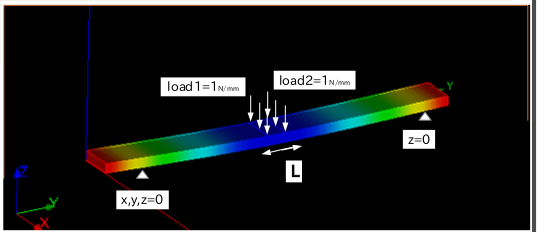
| 理論値($\frac{pl^3}{48EI}+\frac{pl}{4kGA}$) | 1/1 | 1/4(w/1) | 1/4(w/2) | 1/4(w/4) | |
| たわみ | 2.5988 | 2.52680 | 2.56042 | 1.28021 | 0.640016 |
| 要素数 | 約68.9万 | 約61.9万 | 約61.9万 | 約61.9万 | |
| 相対誤差(%) | 2.77 | ◎1.477 | 50.738 | 75.373 |
| 理論値($\frac{pl^3}{48EI}+\frac{pl}{4kGA}$) | 1/1 | 1/4(w/1) | 1/4(w/2) | 1/4(w/4) | |
| たわみ | 2.5988 | 2.52572 | 2.56056 | 1.28025 | 0.64012 |
| 要素 | 約61.5万 | 約62.8万 | 約62.8万 | 約62.8万 | |
| 相対誤差(&) | 2.812 | ◎1.471 | 50.737 | 75.369 |
| 理論値($\frac{pl^3}{48EI}+\frac{pl}{4kGA}$) | 1/1 | 1/4(w/1) | 1/4(w/2) | 1/4(w/4) | |
| たわみ | 2.5981 | 2.52709 | 5.12068 | 2.56034 | 1.28017 |
| 要素 | 約70万 | 約62.8万 | 約62.8万 | 約62.8万 | |
| 相対誤差(&) | 2.7332 | 97.0932 | ◎1.4534 | 50.7267 |
| 曲げ弾性率(GN/m2=GPa) | 圧縮強度(MN/m2=MPa) | 引張強度(MN/m2=MPa) | 曲げ強度(MN/m2=MPa) | せん断強度(MN/m2=MPa) |
| 7.350 | 34.3 | 88.2 | 63.7 | 5.88 |
| 木口面硬さ(硬度)(MN/m2=MPa) | 板目面硬さ(硬さ)(MN/m2=MPa) | |||
| 31.36 | 7.84 |
| 曲げ弾性率(GN/m2=GPa) | 圧縮強度(MN/m2=MPa) | 引張強度(MN/m2=MPa) | 曲げ強度(MN/m2=MPa) | せん断強度(MN/m2=MPa) |
| 11.27 | 44.1 | 137.2 | 88.2 | 9.31 |
| 木口面硬さ(硬度)(MN/m2=MPa) | 板目面硬さ(硬さ)(MN/m2=MPa) | |||
| 42.14 | 11.76 |
| モデル | たわみ |
 | 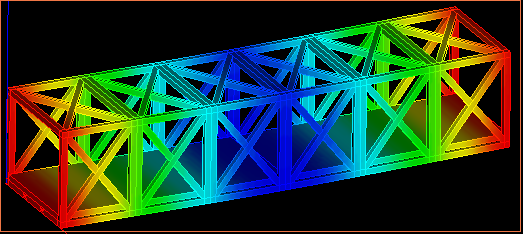 |
| 変位mm | 剛性Nmm2 | 体積mm3 | 比剛性N/mm |
| 0.000686552 | 339784896.1 | 89306.10 | 3804.722 |
| σxx | σyy | σzz |
 |  | 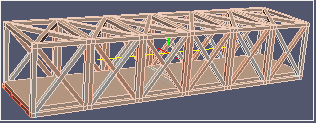 |
 |  |  |
| モデル | たわみ |
 | 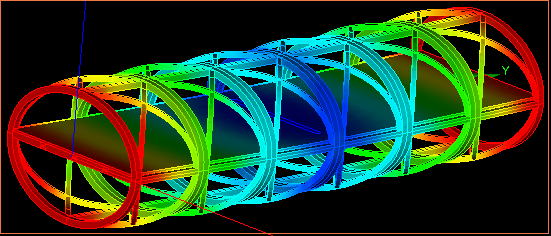 |
| 変位mm | 剛性Nmm2 | 体積mm3 | 比剛性N/mm |
| 0.00238660 | 97745747.09 | 69811.40964 | 1400.14 |
| σxx | σyy | σzz |
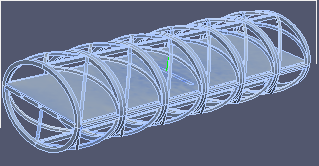 | 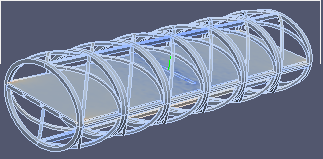 | 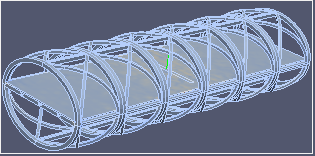 |
 |  |  |
| 応力 | 引張 | 圧縮 |
| σxx | 微増 | 微減 |
| σyy | 半分以下に減少 | 半分に減少 |
| σzz | 二倍に増加 | 微増 |
| σxx | σyy | σzz | |
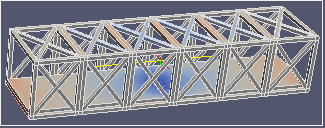 | 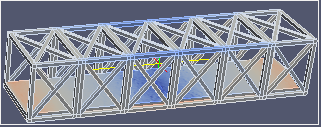 | 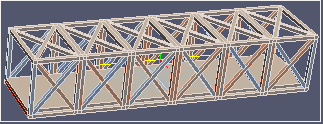 | |
| σxy せん断 | σyz せん断 | σzx せん断 | |
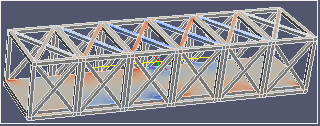 | 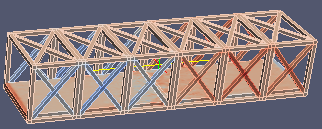 | 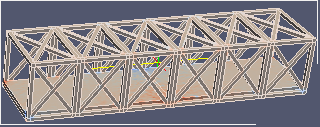 | 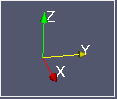 |
| σxx | σyy | σzz | |
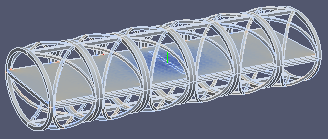 | 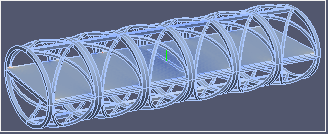 |  | |
 |  |  | |
| σxy せん断 | σyz せん断 | σzx せん断 | |
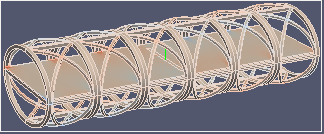 |  |  |
| σxx | σyy | σzz | |
 |  |  | |
| σxy せん断 | σyz せん断 | σzx せん断 | |
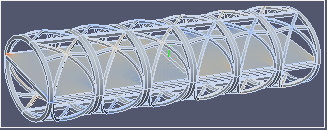 | 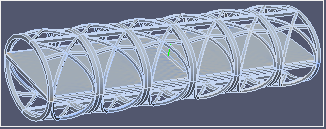 |  |  |
| σxx | σyy | σzz | |
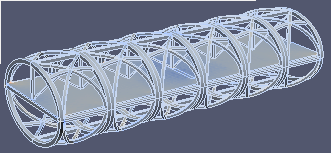 |  |  |  |
| σxy せん断 | σyz せん断 | σzx せん断 | |
 |  |  | 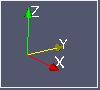 |
| たわみ(載荷部)mm | 剛性 | 体積mm3 | 比剛性 |
| 0.00181751 | 128351425.9 | 80191.79 | 1600.555692 |
| たわみ(フレーム全体) | 剛性 | 体積 | 比剛性 |
| 0.001521625 | 153309783.9 | 80191.79 | 1911.789024 |
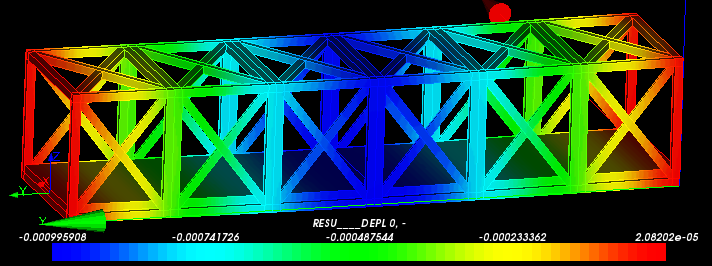
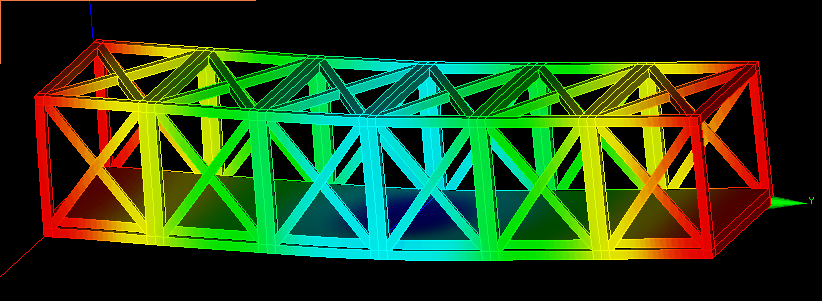
| たわみ(載荷部)mm | 剛性 | 体積mm3 | 比剛性 |
| 0.000995908 | 234238504 | 80191.79 | 2920.978618 |
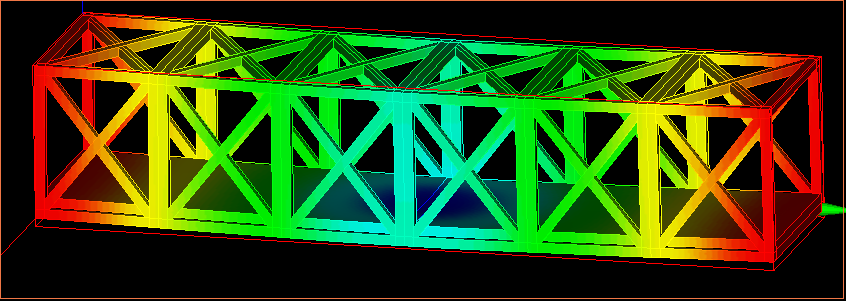
| たわみ(載荷部)mm | 剛性N・mm2 | 体積mm3 | 比剛性 |
| 0.00142101 | 164164924.9 | 86450.09 | 1898.956091 |
| たわみ(フレーム全体) | 剛性 | 体積 | 比剛性 |
| 0.001200905 | 194253500.5 | 86450.09 | 2247.001715 |

| たわみmm | 剛性N・mm2 | 体積mm3 | 比剛性 |
| 0.000708312 | 329346389.7 | 86450.09 | 3809.669715 |
| たわみ(載荷部)mm | 剛性Nmm2 | 体積mm3 | 比剛性 |
| 0.00335914 | 69446346.39 | 162604.69 | 427.0869825 |
| たわみ(フレーム全体) | 剛性 | 体積 | 比剛性 |
| 0.00033643 | 693398329.5 | 162604.69 | 4264.319372 |
| たわみ(載荷部)mm | 剛性Nmm2 | 体積mm3 | 比剛性 |
| 0.00424564 | 54945779.67 | 162604.69 | 337.91018 |
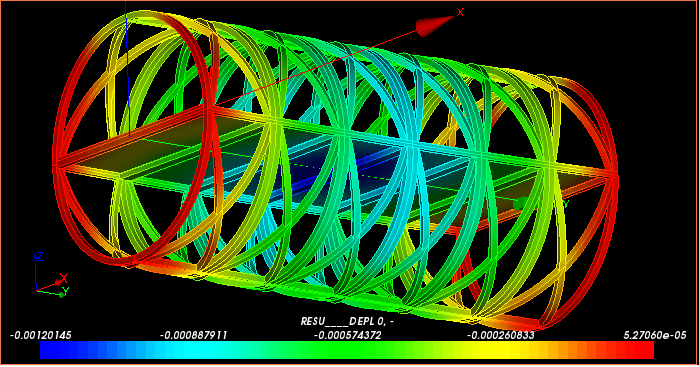
| たわみ(載荷部)mm | 剛性Nmm2 | 体積mm3 | 比剛性 |
| 0.00120145 | 194165383.5 | 162604.69 | 1194.094608 |

| たわみ(載荷部分) | 剛性 | 体積 | 比剛性 |
| 0.00449816 | 51861205.47 | 93350.26 | 555.555019 |
| たわみ(フレーム全体) | 剛性 | 体積 | 比剛性 |
| 0.003360375 | 69420823.57 | 93350.26 | 743.6596702 |
| たわみ | 剛性 | 体積 | 比剛性 |
| 0.00698656 | 33389822.75 | 68020.239007 | 490.8807031 |
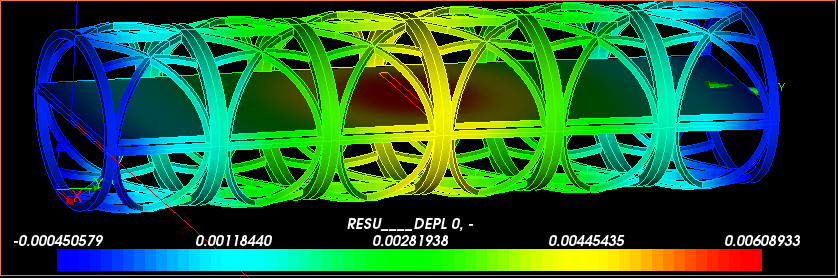
| たわみ(載荷部分) | 剛性 | 体積 | 比剛性 | |
| 0.00354370 | 65826500.24 | 68020.239007 | 967.7928393 |
| たわみ(載荷部分) | 剛性 | 体積 | 比剛性 | |
| 0.00374815 | 62238704.43 | 65786.691349 | 946.0683179 |
| 先端たわみmm | 体積mm3 | 剛性Nmm2 | 比剛性 |
| 0.339572 | 30000 | 1840552.225 | 61.35174 |
| たわみ(理論) | 誤差 | |
| 0.61728 | 0.5501101607 |
| たわみmm(上面下面の平均) | 体積mm3 | 剛性Nmm2 | 比剛性 |
| 0.0003984405 | 76800 | 288625277.8 | 3758.1416 |
| たわみ理論 | 誤差 | たわみ(せん断考慮) | 誤差 |
| 0.00008650466975 | 4.605999897 | 0.0002942006185 | 1.354315644 |
| 断面m | スパンm | たわみm | 理論値たわみ(せん断考慮) | 相対誤差% |
| 5x5 | 200 | 0.283562 | 0.2886049843 | 1.778 |
| 10x10 | 200 | 0.0180301 | 0.0181512 | 0.672 |
| 15x15 | 200 | 0.00358952 | 0.003622755556 | 0.9259 |
| 20x20 | 200 | 0.00117095 | 0.0011628 | 0.7009 |
| 25x25 | 200 | 0.000498945 | 0.000484992 | 2.8769 |
| 30x30 | 200 | 0.000255351 | 0.0002390222 | 0.68314 |
| 35x35 | 200 | 0.000145973 | 0.0001224185923 | 19.24087 |
| 40x40 | 200 | 0.0000929466 | 0.0000722025 | 28.73044 |
| 断面mm | 穴mm | スパンm | たわみm | 理論値たわみ(せん断考慮) | 相対誤差% | 要素数 |
| 30x30 | 5x5 | 200 | 2.403277907e-4 | 2.55283e-4 | 6.223 | 974842 |
| 30x30 | 10x10 | 200 | 2.62897e-4 | 2.79833e-4 | 3.018673 | 922267 |
| 30x30 | 15x15 | 200 | 2.86381e-4 | 2.665783704e-4 | 7.42846 | 869727 |
| 30x30 | 20x20 | 200 | 3.24571e-4 | 3.221230769e-4 | 0.7599 | 759253 |
| 30x30 | 25x25 | 200 | 6.66933e-4 | 6.939915087e-4 | 4.04262614 | 610872 |
| モデル | スパン | たわみ(全体) | たわみ(載荷部) | 剛性(全体) | 剛性(載荷部) | 体積 | 比剛性(全体) | 比剛性(載荷部) |
| ダブルワーレン(1材料) | 240 | 0.001521625 | 0.00181751 | 153309783.9 | 128351425.9 | 80191.79 | 1911.789024 | 1600.555692 |
| ダブルワーレン(2材料) | 240 | 0.000995908 | 234238504 | 80191.79 | 2920.978618 | |||
| X剛結(1材料) | 240 | 0.001200905 | 0.00142101 | 194253500.5 | 164164924.9 | 86450.09 | 2247.001715 | 1898.956091 |
| X剛結(2材料) | 240 | 0.000708312 | 329346389.7 | 86450.09 | 3809.669715 | |||
| 円(1材料) | 240 | 0.00033643 | 0.00335914 | 693398329.5 | 69446346.39 | 162604.69 | 4264.319372 | 427.0869825 |
| 円(1材料床版中央) | 240 | 0.00424564 | 54945779.67 | 162604.69 | 337.91018 | |||
| 円(2材料) | 240 | 0.00120145 | 194165383.5 | 162604.69 | 1194.094608 | |||
| 楕円(1材料) | 240 | 0.003360375 | 0.00449816 | 69420823.57 | 51861205.47 | 93350.26 | 743.6596702 | 555.555019 |
| 楕円(1材料床版中央) | 240 | 0.00698656 | 33389822.75 | 68020.24 | 490.8807031 | |||
| 楕円(2材料) | 240 | 0.00608933 | 38309633.41 | 68020.24 | 563.2093325 |
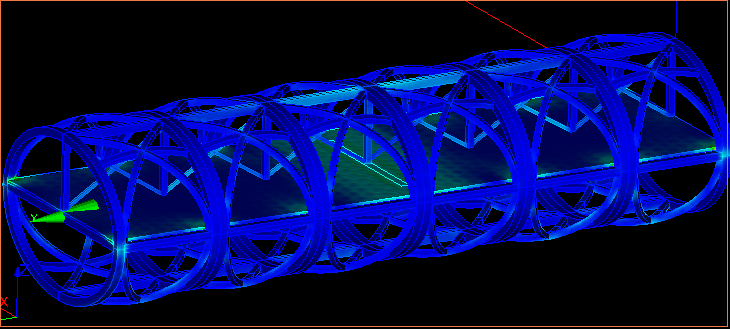
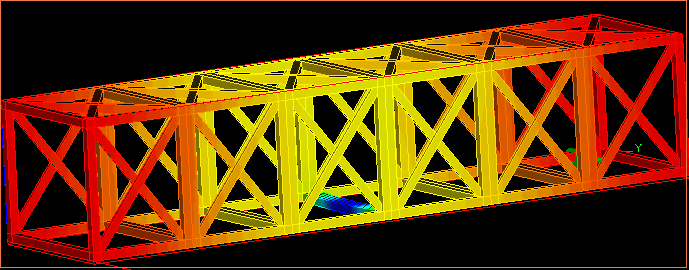


MA=DEFI_MATERIAU(ELAS=_F(E=〜,
NU=〜,),);
MA=DEFI_MATERIAU(ELAS_ORTH=_F(E_L=〜,
E_T=〜,
E_N=〜,
G_LT=〜,
G_TN=〜,
G_LN=〜,
NU_LT=〜,
NU_TN=〜,
NU_LN=〜,),);
MA=DEFI_MATERIAU(ELAS_ORTH=_F(E_L=1000,
E_T=10,
E_N=10,
G_LT=10,
G_TN=10,
G_LN=10,
NU_LT=0.3,
NU_TN=0.3,
NU_LN=0.3,),);
FORCE_ARETE=(
_F(GROUP_MA='pfz', !+FZ
FZ=○○,),
_F(GROUP_MA='pfx', ! +FX
FX=○○,),
_F(GROUP_MA='mfx', ! -FX
FX=-○○,),
_F(GROUP_MA='mfz', ! -FZ
FZ=-○○,),
| 荷重・たわみの方向 | 荷重 | たわみ |
| +Z | FZ=1000N/mm | 2.32019e06 |
| 荷重・たわみの方向 | 荷重 | たわみ |
| -Z | FZ=-1000N/mm | 2.32018e6 |
| 荷重・たわみの方向 | 荷重 | たわみ |
| +X | FX=1000N/mm | 974292=0.974292e6 |
| 荷重・たわみの方向 | 荷重 | たわみ |
| -X | FX=-1000N/mm | 974292=0.974292e6 |
| コマンド | 意味 |
| RESU_DEPL | 変位 |
| RESU_SIGM_NOEU | 垂直応力とせん断応力 |
| RESU_SIEQ_NOEU | 相当応力(ミーゼス、トレス、主応力) |
| sequence | 開始時間と終了時間を指定して、その間の指定した数のフレームで一定の速度で再生する。 |
| real time | 開始時間と終了時間を指定して、その間で再生出来るようにレンダリングすつフレーム数が調整される。 |
| snap to timesteps | データ内のタイムステップ数に従ってフレームを再生する。 |
MA=DEFI_MATERIAU(ELAS=_F(E=xxx,
NU=xxx,),);
MA1=DEFI_MATERIAU(ELAS=_F(E=xxx,
NU=xxx,),);
MA2=DEFI_MATERIAU(ELAS=_F(E=△△△,
NU=△△△,),);
MATE=AFFE_MATERIAU(MAILLAGE=MAIL,
AFFE=_F(TOUT='OUI',
MATER=MA,),);
MATE=AFFE_MATERIAU(MAILLAGE=MAIL,
AFFE=(_F(GROUP_MA='Group○',
MATER=MA1,),
_F(GROUP_MA='Group□',
MATER=MA2,),),);
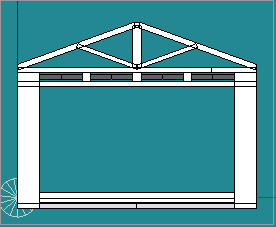
{\bf 図-\ref{14}}に示すように・・・
\begin{figure}[h]
\begin{center}
\includegraphics[width=100mm]{1per4model.eps}
\end{center}
\caption{1/4解析の境界条件}
\label{14}
\end{figure}
platex aaa.tex
pxdvi aaa.dvi
dvipdfm aaa
evince aaa.pdf
\begin{figure}[h]
\begin{center}
\includegraphics[width=画像の幅mm]{ファイル名.eps}
\end{center}
\caption{タイトル}
\end{figure}
\vspace{○mm}
\begin{table}[htb]
\caption{解析結果}
\begin{tabular}{|c|c|c|} \hline
& ダブルワーレン &X剛結\\ \hline \hline
たわみ($mm$) &$9.95908x70^{-4}$&$7.08312x10^{-4}$\\ \hline
剛性($Nmm^2$)&234238504 &329346390\\ \hline
体積($mm^3$) &80191.8 &86450.1\\ \hline
比剛性 &2920.98 &3809.67\\ \hline
\end{tabular}
\end{table}
\vspace{○mm}
タイトルの上下や、表、図の上下の余白を調節出来る。
値を負にすると、上に詰まっていく。多分
:w
:!platex aaa.texプレビュー画面でクリックすれば更新される。
:!pxdvi aaa&
2^3これで${2^3}$になる
\begin{itemize}
\item あいうえお
\item かきくけこ
\item さしすせそ
\end{itemize}
| コマンド | サイズ | |
| \tiny | 5pt | |
| \scriptsize | 7pt | |
| \footnotesize | 8pt | |
| \small | 9pt |
| 日付 | 時間帯 | 作業時間(hr) | 内容 | 立会 |
| 4/9 | 18:00-20:00 | 2 | 構造力学 | 鈴木、伊藤、高橋 |
| 4/9 | 20:00-20:30 | 0.5 | タイピング練習、パソコン操作練習 | 伊藤(タイムを測った人) |
| 4/10 | 11:20-11:30 | 10/60 | タイピング練習 | |
| 4/10 | 15:30-17:30 | 2 | 構造力学 | |
| 4/10 | 20:00-20:10 | 10/60 | タイピング練習 | |
| 4/11 | 19:10-19:20 | 10/60 | タイピング練習 | |
| 4/11 | 22:30-22:40 | 10/60 | タイピング練習 | |
| 4/11 | 14:00-15:00 | 1 | 構造力学 | |
| 4/11 | 21:50-22:10 | 20/60 | とりあえず六角形の橋を作って、解析してみるタイピング練習、パソコン練習 | |
| 4/13 | 16:00-17:00 | 1 | vi課題カレンダー | |
| 4/13 | 22:00-24:00 | 2 | パソコン操作練習 | |
| 4/14 | 17:00-19:00 | 2 | 構造力学、パソコン練習 | |
| 4/16 | 19:00-22:00 | 2 | タイピング練習、パソコン練習、構造力学 | |
| 4/21 | 16:00-17:00 | 1 | fortran課 | |
| 4/21 | 16:00-20:00 | 4 | fortran課題 | |
| 4/30 | 13:00-14:30 | 1.5 | 文献講読 | |
| 4月計 | 20 | |||
| 5/8 | 21:00-22:30 | 1.5 | salome、文献 | |
| 5/11 | 16:00-17:00 | 1 | salome | |
| 5/25 | 16:00-18:00 | 2 | aster | 線載荷POST PROが出ないdeta |
| 5/28 | 22:30-24:00 | 1.5 | aster線載荷2.8 | |
| 5/31 | 23:00-0:30 | 1.5 | aster | |
| 5月計 | 7.5 | |||
| 6/3 | 23:00-1:00 | 2 | salome六角形 | |
| 6/4 | 23:00-1:30 | 2.5 | salome、compound1基準六角形 | |
| 6/11 | 0:00-1:30 | 1.5 | salome | |
| 6/14 | 17:00-19:30 | 2.5 | salome | |
| 6/15 | 22:00-1:00 | 3 | salome | |
| 6/16 | 22:00-2:00 | 4 | salome | |
| 6/17 | 11:30-1:00 | 1.5 | salome | |
| 6/18 | 13:30-15:00 | 1.5 | salome | |
| 6/21 | 22:30-23:00 | 0.5 | 文献 | |
| 6月計 | 19 | |||
| 7/11 | 8:30-12:00 | 3.5 | salome | 六角形はエラーで断念、五角形作成 |
| 7/11 | 19:00-21:00 | 2 | salome | 五角形エラー |
| 7/12 | 8:00-11:00 | 3 | salomeエラーたくさん | |
| 7月計 | 8.5 | |||
| 8/23 | 8:30-17:00 | 8.5 | salome | |
| 8/24 | 8:30-17:00 | 8.5 | salome | |
| 8/25 | 8:30-17:00 | 8.5 | salome | |
| 8/27 | 9:00-16:00 | 7 | salome | |
| 8/28 | 9:00-20:00 | 9 | salome | |
| 8/29 | 8:30-11:30 | 3 | salome、astk | |
| 8/31 | 10:00-17:00 | 5 | salome、astk | |
| 8月計 | 49.5 | |||
| 9/1 | 9:00-19:30 | 8 | salome | |
| 9/3 | 9:30-19:00 | 8.5 | salome 誤差調べ | |
| 9/6 | 9:00-18:00 | 8 | salome 誤差調べ | |
| 9/7 | 9:00-12:00 | 3 | salome 2材料解く練習 | |
| 9/8 | 9:00-15:00 | 5 | salome 2材料 | |
| 9/9 | 9:00-19:00 | 8 | salome 2材料 astk | |
| 9/10 | 9:00-15:00 | 5 | astk 3dプリンタ | |
| 9/12 | 17:00-19:00 | 2 | でーたまとめ | |
| 9/13 | 9:00-18:00 | 6 | salome 練習 | |
| 9/15 | 8:30-19:30 | 7 | salome | |
| 9/16 | 6:30-19:00 | 7 | salome | |
| 9/18 | 12:00-19:00 | 3.5 | tex | |
| 9/19 | 13:00-21:30 | 5 | tex | |
| 9/20 | 12:00-16:30 | 2.5 | tex | |
| 9/21 | 12:00-15:30 | 3.5 | tex | |
| 9/22 | 11:00-20:00 | 8 | tex、スライド | |
| 9/23 | 9:00-18:30 | 4.5 | tex、スライド | |
| 9/25 | 10:00-17:00 | 4 | tex、スライド | |
| 9/27 | 12:00-1:00 | 3 | スライド、発表練習 | |
| 9/29 | 10:00-15:00 | 2 | 発表練習 | |
| 9/29 | 17:00-20:00 | 2 | salome | |
| 9月計 | 105.5 | |||
| 10/7 | 9:00-16:30 | 4 | salome-paraview | |
| 10/8 | 9:00-21:30 | 6 | paraview、tex | |
| 10/9 | 9:00-19:00 | 6 | salome、paraview | |
| 10/10 | 11:00-20:30 | 4 | salome Xモデルに縦桁を作り解析 | |
| 10/11 | 11:00-16:00 | 2 | salome 縦桁モデル解析 | |
| 10/12 | 9:00-17:00 | 4 | salome 縦桁モデル解析 | |
| 10/13 | 13:00-20:00 | 4 | salome paravis | |
| 10/14 | 9:00-16:00 | 5 | salome paravis | |
| 10/15 | 10:30-16:00 | 5 | 3d | |
| 10/16 | 10:30-17:00 | 5 | salome | |
| 10/20 | 9:00-21:00 | 9 | salome | |
| 10/21 | 9:30-18:00 | 4 | salome | |
| 10/22 | 10:00-22:00 | 5 | 木材利用シンポジウム、salome阿蘇望橋の類似モデルを作る | |
| 10/23 | 10:00-19:00 | 5 | salome 阿蘇望橋モデル | |
| 10/24 | 9:30-16:00 | 4 | salome 阿蘇望橋モデル | |
| 10/26 | 12:00-20:30 | 4.5 | salome 阿蘇望橋モデル | |
| 10/28 | 16:00-16:30 | 0.5 | salome meshが切れない。自分のpcだとメモリ不足。他のpcでもエラーで一部切れない。 | |
| 10/29 | 9:00-12:00 | 3 | salome meshエラー | |
| 10/30 | 12:00-15:00 | 2 | salome meshエラー | |
| 10/31 | 9:00-22:00 | 9 | salome 1/4解析 | |
| 10月計 | 91 | |||
| 11/1 | 12:00-15:00 | 3 | salome 阿蘇望橋1/4解析 meshエラー | |
| 11/2 | 9:00-19:00 | 6 | 1/4、asterで異方性 | |
| 11/3 | 9:00-18:00 | 4 | meshエラー | |
| 11/4 | 10:00-20:00 | 3 | meshエラー | |
| 11/5 | 10:00-18:00 | 2 | meshエラー | |
| 11/6 | 9:00-13:00 | 3 | gmeshで切ったけど、エラー | |
| 11/7 | 20:00-23:00 | 3 | meshエラー解消 | |
| 11/8 | 12:30-15:00 | 2.5 | 阿蘇望橋aster | |
| 11/9 | 10:00-13:00 | 3 | 1/4解析の調査 | |
| 11/10 | 9:00-17:00 | 4 | 1/4解析実験 | |
| 11/11 | 10:00-19:00 | 5 | 1/4解析調査 | |
| 11/13 | 9:30-23:00 | 4 | 1/4解析 | |
| 11/14 | 13:00-23:00 | 4 | 1/4kaiseki | |
| 11/15 | 9:30-13:30 | 3 | 1/4解析まとめ | |
| 11/16 | 10:00-11:30 | 1.5 | 楕円モデル1/4解析 | |
| 11/17 | 9:00-12:00 | 2 | 楕円モデル1/4解析 | |
| 11/19 | 9:00-17:00 | 2.5 | 楕円モデル1/4解析 | |
| 11/20 | 18:30-20:00 | 1.5 | eficasの使い方をまさとしに聞く | |
| 11/21 | 11:00-16:00 | 3 | astk bomboo | |
| 11/22 | 16:00-18:00 | 2 | salome | |
| 11/24 | 9:00-1:00 | 4 | 1/4kaiseki | |
| 11/25 | 9:00-21:00 | 3 | hikaku | |
| 11/26 | 15:00-21:00 | 5 | 五角形モデル作成 | |
| 11/27 | 9:00-19:00 | 4 | 五角形モデル作成 | |
| 11/28 | 10:30-16:00 | 4 | gokakukei | |
| 11/29 | 13:00-17:30 | 1.5 | gokakukei | |
| 11/30 | 10:00-16:00 | 4 | gokakukeitukurinaosi | |
| 11/30 | 20:30-22:00 | 1 | 1/4kaiseki | |
| 11月計 | 84.5 | |||
| 12/1 | 10:00-18:00 | 4 | 五角形モデル作り直し めっしゅ切れた 次は解析 | |
| 12/2 | 21:00-23:00 | 2 | 1/4解析 | |
| 12/3 | 12:00-17:00 | 5 | 1/4解析 | |
| 12/4 | 10:30-0:00 | 4 | 楕円モデル作り直し | |
| 12/5 | 10:00-15:00.21:30-22:30 | 5 | 楕円モデル解析しなおし | |
| 12/6 | 14:00-16:00 | 2 | tex | |
| 12/7 | 10:00-16:00 | 3 | 1/4解析 tex | |
| 12/8 | 12:00-22:30 | 3 | 応力調べ tex | |
| 12/9 | 10:00-16:00 | 1 | 応力調べ tex | |
| 12/11 | 9:30-16:00 | 2 | tex mesh ouryoku | |
| 12/14 | 9:00-23:30 | 4 | tex グラフ | |
| 12/15 | 13:00-23:30 | 4 | tex グラフ | |
| 12/16 | 10:00-18:00 | 4 | tex スライド 無次元化した式の根拠はないけど、将来的にスパンや体積が異なるモデルと比較できるようにしている。 東北支部に関するお金の相談を金曜日にする。 | |
| 12/17 | 9:30-16:00 | 1.5 | tex スライド | |
| 12/18 | 12:00-17:00 | 3 | tex 応力調べ | |
| 12/19 | 13:00-15:30 | 2.5 | tex slide 対傾構について調べる | |
| 12/20 | 11:00-16:00 | 0.5 | ||
| 12/21 | 11:00-16:00 | 0.5 | 発表練習 | |
| 12/22 | 10:00-15:00 | 4 | 中間発表 | |
| 12/23 | 11:00-14:30 | 3 | 楕円モデル作り直し | |
| 12/24 | 9:00-22:30 | 3.5 | 楕円モデル作り直し | |
| 12月計 | 61.5 | |||
| 1/6 | 9:00-19:00 | 4.5 | slide | |
| 1/7 | 10:00-15:30 | 3 | texslide つくりなおし | |
| 1/8 | 10:00-16:00 | 4 | 足アーチモデル作り直し | |
| 1/9 | 9:30-15:00 | 5.5 | 概要作り直し | |
| 1/10 | 14:00-16:00 | 2 | 足アーチモデル解析 | |
| 1/11 | 12:30-19:00 | 6.5 | 足アーチ解析 | |
| 1/13 | 10:30-16:30 | 3 | 卒論、概要修正 | |
| 1/14 | 10:00-18:30 | 2.5 | 概要・スライド訂正、発表練習見る。 | |
| 1/15 | 9:00-16:00 | 4 | 概要、スライド、発表練習 | |
| 1/18 | 9:30-17:00 | 4 | 概要、スライド、発表練習 | |
| 1/19 | 9:00-11;30 | 2.5 | 発表練習 | |
| 1/19 | 17:00-21:00 | 4 | スライドなおし | |
| 1/20 | 9:00-16:00 | 4 | スライド、概要直し | |
| 1/21 | 10:00-16:00 | 2 | 〃 | |
| 1/25 | 15:00-17:00 | 2 | 〃 | |
| 1/26 | 12:00-14:00 | 2 | 発表練習 | |
| 1/28 | 12:00-18:00 | 4 | 卒論、発表練習 | |
| 1/29 | 12:00-18:00 | 4 | 卒論、発表練習 | |
| 1/30 | 10:00-17:00 | 4 | 〃 | |
| 1/31 | 10:00-19:00 | 6 | 〃 | |
| 1月計 | 73.5 | |||
| 2/1 | 11:00-21:00 | 3 | 発表練習 卒論 |
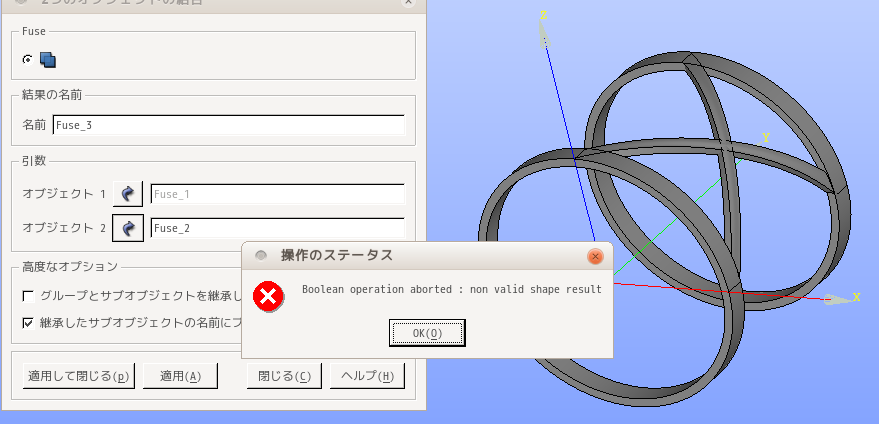
Boorean operation aborted non valid shape resultとなってfuseできなくなる。
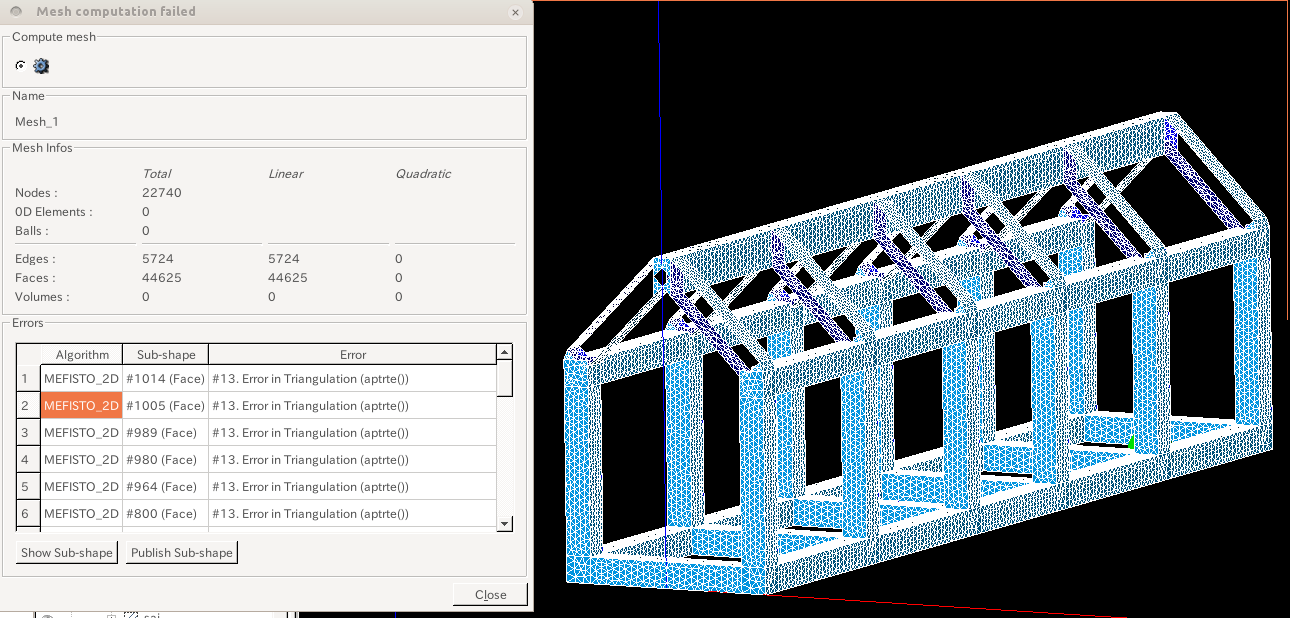
<EXCEPTION> <CALCULEL2_74> Erreur utilisateur dans un calcul élémentaire : Le matériau est nécessaire sur la maille : M440491 - option de calcul élémentaire : RIGI_MECA - type_element : MECA_TETRA4 Conseils : * Peut-etre avez-vous oublié de renseigner le mot clé CHAM_MATER dans la commande courante. * Dans la commande AFFE_MATERIAU, avez-vous affecté un matériau sur la maille incriminée ?
| 日付 | タイム |
| 4/9(Thu) | 4'42" |
| 4/10(Fri) | 4'10" |
| 4/10(Fri) | 4'04" |
| 4/13(mon) | 2'57" |
| 5/3(sun) | 3'11" |
目標 3'00''以内 目標 2'30"以内
現在、日本では森林が増えすぎているという現状がある。 森林面積は一定であるのに、森林蓄積が40年間で5.5倍に増加した。 日本はこれから成長した森林を活かすべき時代に突入したと言える。 しかし、コストの面から日本は木材の約7割を輸入材に頼っており、全く有効利用できていない。 そこで、これから環境負荷低減性や低建設コストと言った特徴を持つ近代木橋の有効利用が更に見直されていくのではないかと考えた。 また、近年インフラの老朽化といったことが叫ばれており、屋根付き木橋といった老朽化対策・長寿命化対策の機能を備えた木橋であれば時代背景と合致しており、仮設が検討できるのではないかと考えたため、屋根付き木橋の研究をしている。
・森林面積:2500万ha(国土の約7割)40年間横ばい しかし人工林は30%増加して1000万ha ・森林蓄積:森林を構成する樹木の幹の体積 40年間で5.5倍に増加
・日本の自国の森林資源に対する年間伐採量 0.5%
・森林面積が増加していないのに、森林蓄積が増加している理由 戦後に植林されたものが成長し収穫期を迎えている。 輸入材が増加して国産材が使用されなくなってきている。
・これから日本は成長した森林を活かすべき時代に突入したと言える。
http://www.shinrin-ringyou.com/forest_japan/menseki_tikuseki.php