- 幅:0.1m,高さ0.1m,軸方向:1m
- ヤング率:206GPa
- 降伏点:235MPa
合板応急橋の試験データはk2のdata/gouhanの中

MAIN MENUに戻る。
MAIN MENUに戻る。
MAIN MENUに戻る。
MAIN MENUに戻る
MAIN MENUに戻る
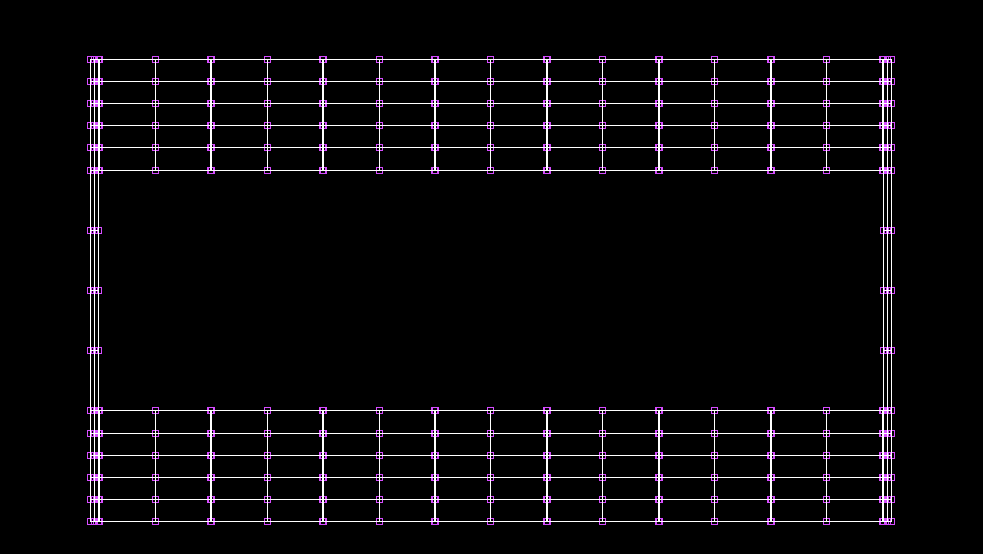
| 幅員方向(m) | 変位(mm) |
| 0 | 5.93122 |
| 0.0045 | 5.95046 |
| 0.009 | 5.96992 |
| 0.0095 | 5.99278 |
| 0.01 | 5.99186 |
| 0.07 | 6.33373 |
| 0.13 | 6.78022 |
| 0.1305 | 6.7855 |
| 0.131 | 6.78709 |
| 0.191 | 7.1762 |
| 0.251 | 7.53936 |
| 0.2515 | 7.54372 |
| 0.252 | 7.54454 |
| 0.312 | 7.77123 |
| 0.372 | 7.98269 |
| 0.3725 | 7.9854 |
| 0.373 | 7.98457 |
| 0.433 | 7.99928 |
| 0.493 | 7.98457 |
| 0.4935 | 7.9854 |
| 0.494 | 7.98269 |
| 0.554 | 7.77456 |
| 0.614 | 7.54454 |
| 0.6145 | 7.54372 |
| 0.675 | 7.53936 |
| 0.735 | 7.1462 |
| 0.7355 | 6.78709 |
| 0.736 | 6.7855 |
| 0.796 | 6.78022 |
| 0.856 | 6.33373 |
| 0.8565 | 5.99186 |
| 0.857 | 5.99278 |
| 0.8615 | 5.96992 |
| 0.866 | 5.95046 |
$\bar{\sigma}=\sqrt{\frac{3}{2}}\sqrt{S_{xx}^2+S_{yy}^2+S_{zz}+2(S_{xy}^2+S_{yz}^2+S_{zx}^2)}$
$S_{xx}=\sigma_{xx}-\sigma_{m}$ $S_{yy}=\sigma_{yy}-\sigma_{m}$ $S_{zz}=\sigma_{zz}-\sigma_{m}$ $S_{xy}=\sigma_{xy}$ $S_{yz}=\sigma_{yz}$ $S_{zx}=\sigma_{zx}$
$\sigma_{m}=\frac{1}{3}(\sigma_{xx}+\sigma_{yy}+\sigma_{zz})$
プレストレスを考慮する場合 $\bar{\sigma}=\sqrt{\frac{3}{2}(\sigma_{zz}^2+2\sigma_{zx}^2)}$
| 荷重(N) | $\sigma_{Mises}$ | 相当応力 | $\sigma_{xx}$ | $\sigma_{yy}$ | $\sigma_{zz}$ | $\tau_{xy}$ | $\tau_{yz}$ | $\tau_{zx}$ | 変位(m) |
| 1000 | 0.0860258 | 0.086016067 | 0 | 0 | 0 | 0 | 1.34224E-18 | 0.04966140 | 6.29E-10 |
| 5000 | 0.430129 | 0.430080339 | 0 | 5.18696E-15 | 8.10463E-17 | 0 | 0 | 0.248307 | 3.14584E-9 |
| 10000 | 0.860258 | 0.860160679 | 0 | 1.037E-14 | 1.620E-16 | 0 | 3.13985E-18 | 0.496614 | 6.29167E-9 |
| 15000 | 1.29039 | 1.29024102 | 0 | 0 | 1.29674E-15 | 0 | 2.148E-17 | 0.744921 | 9.4375E-9 |
| 20000 | 1.72052 | 1.720321359 | 0 | 0 | 0 | 0 | 1.514E-17 | 0.993228 | 1.25833E-8 |
| 25000 | 2.15064 | 2.150393039 | 8.299E-14 | 0 | 6.4837E-16 | 0 | 4.29518E-17 | 1.24153 | 1.573E-8 |
| 26000 | 2.23667 | 2.236424003 | 0 | 0 | 0 | 0 | 2.269E-17 | 1.2912 | 1.63583E-8 |
| 29000 | 2.49475 | 2.494464932 | 0 | 0 | 0 | 0 | 2.269E-17 | 1.44018 | 1.82458E-8 |
| 30000 | 2.58077 | 2.580478575 | 0 | 0 | 0 | 0 | 8.347E-17 | 1.48984 | 1.8875E-8 |
| 荷重(N) | $\sigma_{Mises}$ | 相当応力 | $\sigma_{xx}$ | $\sigma_{yy}$ | $\sigma_{zz}$ | $\tau_{xy}$ | $\tau_{yz}$ | $\tau_{zx}$ | 変位(m) |
| 1000 | 0.0860258 | 0.086016067 | 0 | 0 | 0 | 0 | 1.34224E-18 | 0.04966140 | 6.29E-10 |
| 5000 | 0.430129 | 0.430080339 | 0 | 5.18696E-15 | 8.10463E-17 | 0 | 0 | 0.248307 | 3.14584E-9 |
| 10000 | 0.860258 | 0.860160679 | 0 | 1.037E-14 | 1.620E-16 | 0 | 3.13985E-18 | 0.496614 | 6.29167E-9 |
| 15000 | 1.29039 | 1.29024102 | 0 | 0 | 1.29674E-15 | 0 | 2.148E-17 | 0.744921 | 9.4375E-9 |
| 20000 | 1.72052 | 1.720321359 | 0 | 0 | 0 | 0 | 1.514E-17 | 0.993228 | 1.25833E-8 |
| 25000 | 2.15064 | 2.150393039 | 8.299E-14 | 0 | 6.4837E-16 | 0 | 4.29518E-17 | 1.24153 | 1.573E-8 |
| 26000 | 2.23667 | 2.236424003 | 0 | 0 | 0 | 0 | 2.269E-17 | 1.2912 | 1.63583E-8 |
| 29000 | 2.49475 | 2.494464932 | 0 | 0 | 0 | 0 | 2.269E-17 | 1.44018 | 1.82458E-8 |
| 30000 | 2.58077 | 2.580478575 | 0 | 0 | 0 | 0 | 8.347E-17 | 1.48984 | 1.8875E-8 |
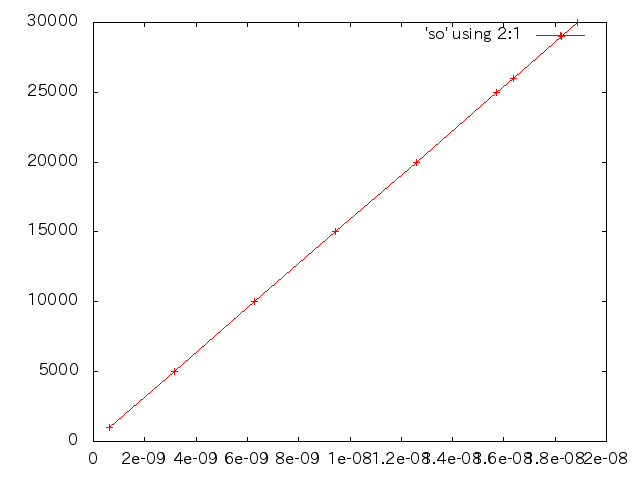
| 荷重(N) | $\sigma_{Mises}$ | 相当応力 | $\sigma_{xx}$ | $\sigma_{yy}$ | $\sigma_{zz}$ | $\tau_{xy}$ | $\tau_{yz}$ | $\tau_{zx}$ | 変位(m) |
| 1000 | 0.701445 | 0.812 | 0.544447 | 0.085576 | -0.079059 | -0.0129 | 0.00276 | 0.255 | 5.232-9 |
| 10000 | 7.01445 | 8.066 | 5.44447 | 0.855756 | -0.79059 | -0.129121 | 0.0275558 | 2.54534 | 5.232E-8 |
| 15000 | 10.5217 | 12.18493247 | 8.1667 | 1.28363 | -1.18589 | -0.193681 | 0.0413337 | 3.818 | 7.84864E-8 |
| 20000 | 12.2935 | 14.74743448 | 9.96516 | 2.07722 | -1.06716 | -0.200825 | 0.0464743 | 4.48041 | 1.08583E-7 |
| 25000 | 11.1995 | 14.17433036 | 8.53547 | 3.6565 | -0.334745 | -0.034878 | 0.0211037 | 4.8786 | 1.75359E-7 |
| 30000 | 10 | 4.51615 | 3.26422 | -1.53686 | -0.118612 | -0.00761243 | 4.95781 | 4.65926E-7 |
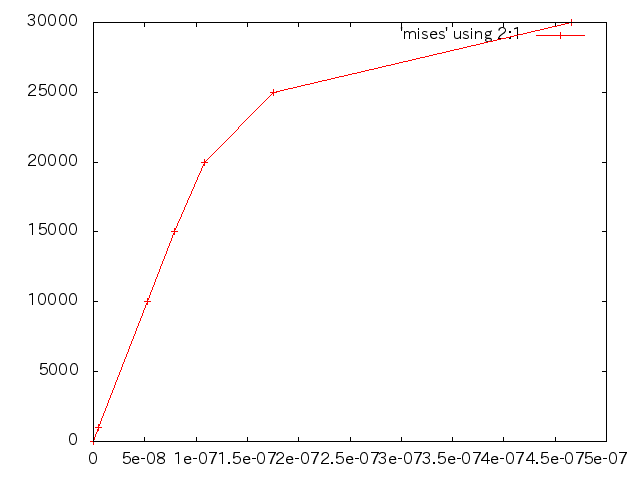
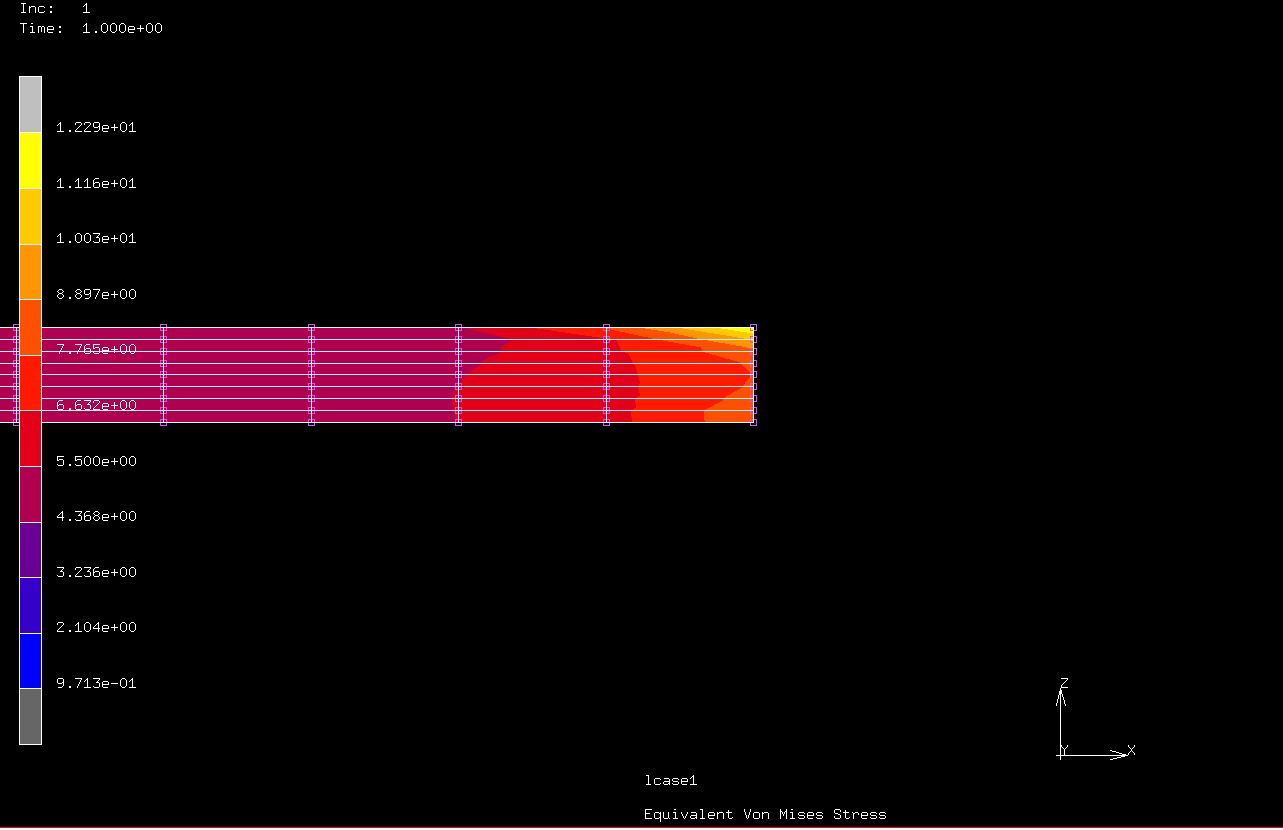
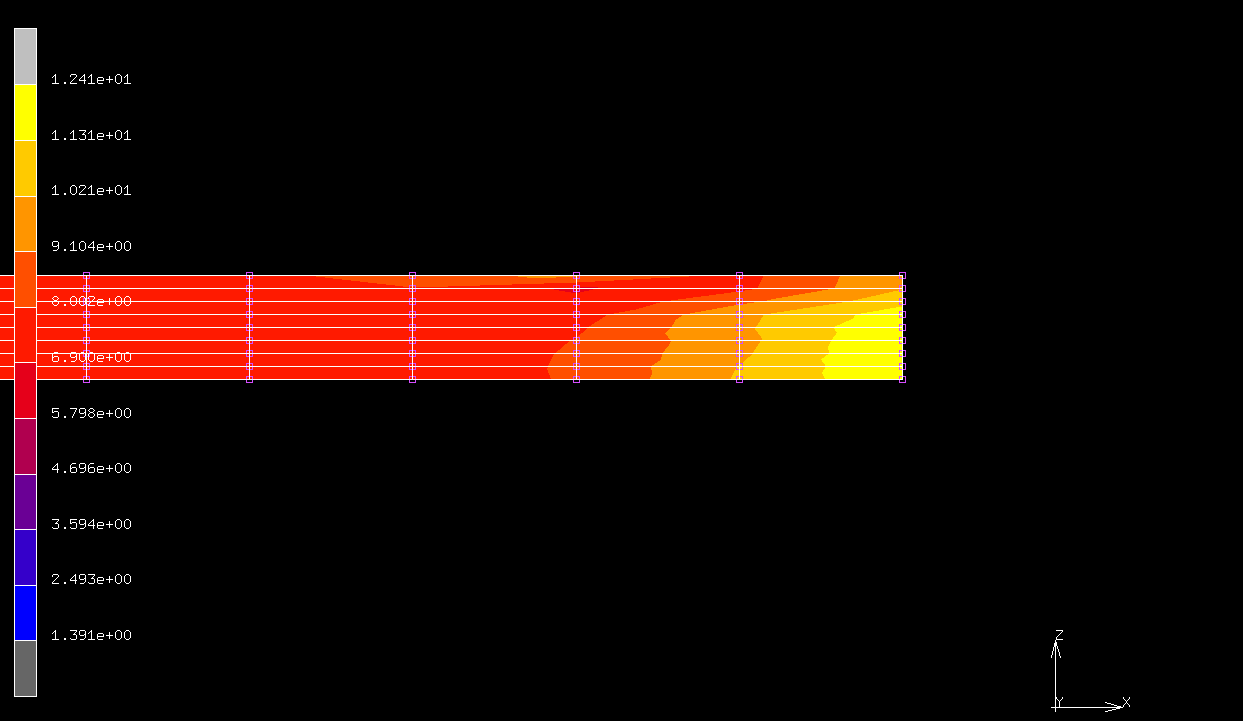
| 荷重 | 変位(m) |
| 0 | 0 |
| 1000 | 5.23757E-6 |
| 5000 | 2.61878E-5 |
| 10000 | 5.23757E-5 |
| 20000 | 1.08686E-4 |
| 21000 | 1.18595E-4 |
| 22000 | 1.3037E-4 |
| 23000 | 1.42581E-4 |
| 24000 | 1.55667E-4 |
| 25000 | 1.7549E-4 |
| 30000 | 5.56882E-4 |
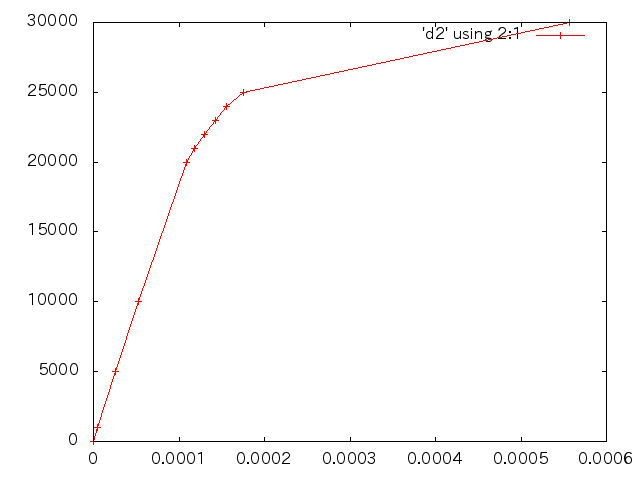
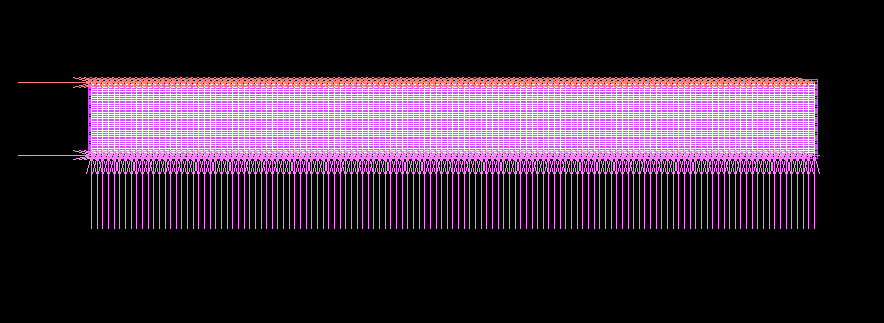
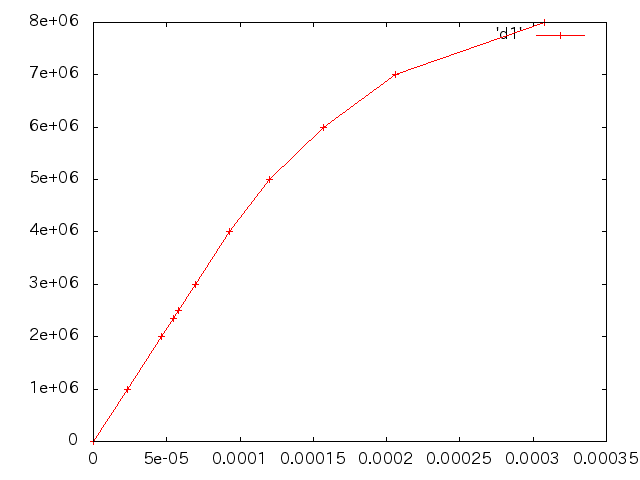
| 荷重(N) | 変位(m) |
| 1.00E6 | 2.315E-5 |
| 2.00E6 | 4.630E-5 |
| 2.35E6 | 5.440E-5 |
| 2.50E6 | 5.787E-5 |
| 3.00E6 | 6.945E-5 |
| 4.00E6 | 9.260E-5 |
| 5.00E6 | 1.204E-4 |
| 6.00E6 | 1.569E-4 |
| 7.00E6 | 2.058E-4 |
| 8.00E6 | 3.079E-4 |
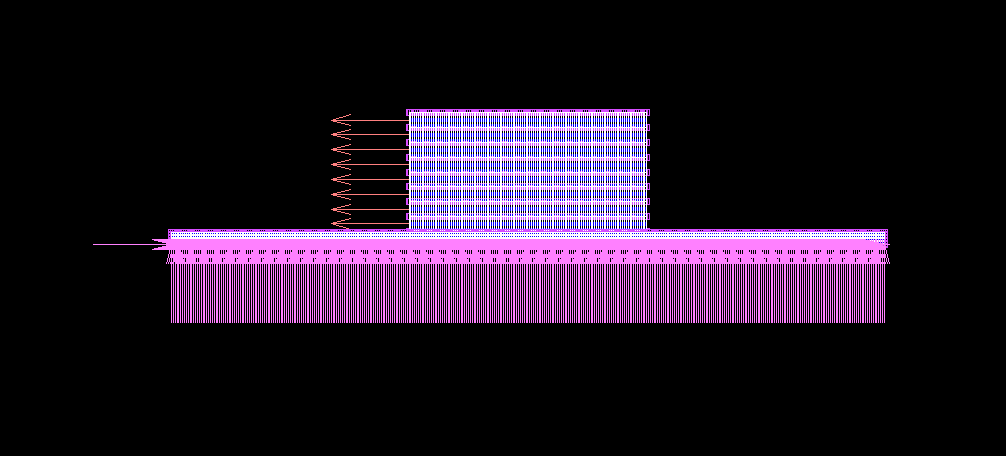
| 引張力(N) | せん断応力σzx | 変位(m) |
| 0.5 | 1.992E-11 | 3.220E-5 |
| 0.6 | 2.392E-11 | 3.866E-5 |
| 0.7 | 2.794E-10 | 4.518E-5 |
| 0.8 | 3.209E-10 | 5.182E-5 |
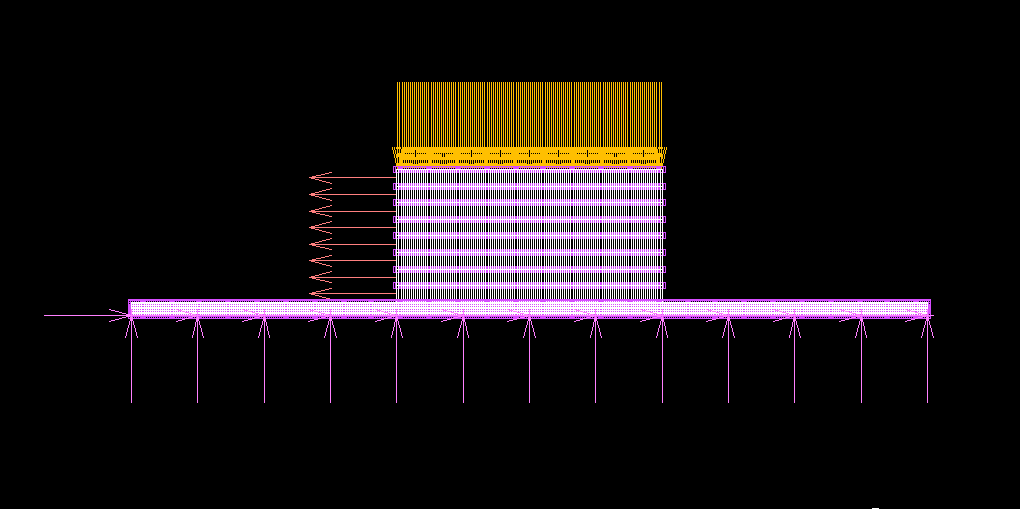
| 応力(MPa) | 変位(m) | 鋼材と木材のズレ(m) | せん断応力σzx(MPa) |
| 0.5 | 1.577E-08 | 0 | 0.256 |
| 0.6 | 1.893E-08 | 0 | 0.307 |
| 0.7 | 2.208E-08 | 0 | 0.358 |
| 0.8 | 2.523E-08 | 0 | 0.409 |
| 0.9 | 2.839E-08 | 0 | 0.461 |
| 1.0 | 3.074E-06 | 3.044E-06 | 0.501 |
| 1.1 | 1.573E-05 | 1.570E-05 | 0.519 |
| 1.2 | 0.12519 | 0.12519 | 0.677 |
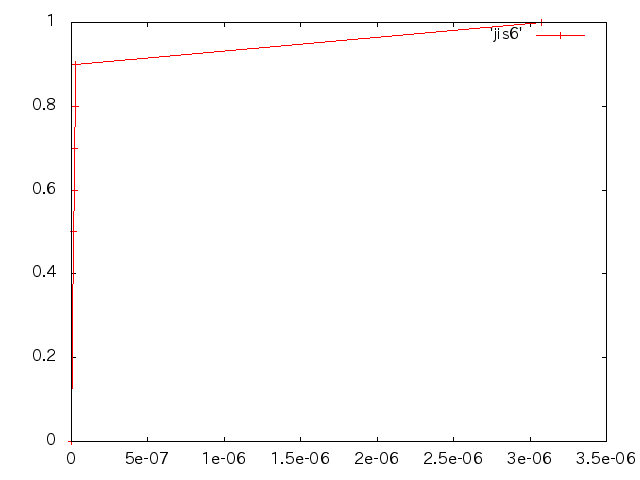
| 引張力(N) | 変位(m) | 鋼材と木材のズレ(m) | せん断応力σzx(MPa) |
| 0.5 | 1.971E-12 | 0 | 3.199E-05 |
| 0.6 | 2.366E-12 | 0 | 3.839E-05 |
| 0.7 | 2.760E-12 | 0 | 4.479E-05 |
| 0.8 | 3.154E-12 | 0 | 5.118E-05 |
| 0.9 | 3.549E-12 | 0 | 5.759E-05 |
| 0.99 | 3.909E-12 | 0 | 6.342E-05 |
| 1.0 | 2.484E-10 | 2.446E-10 | 6.328E-05 |
| 1.1 | 1.717E-09 | 1.713E-09 | 6.571E-05 |
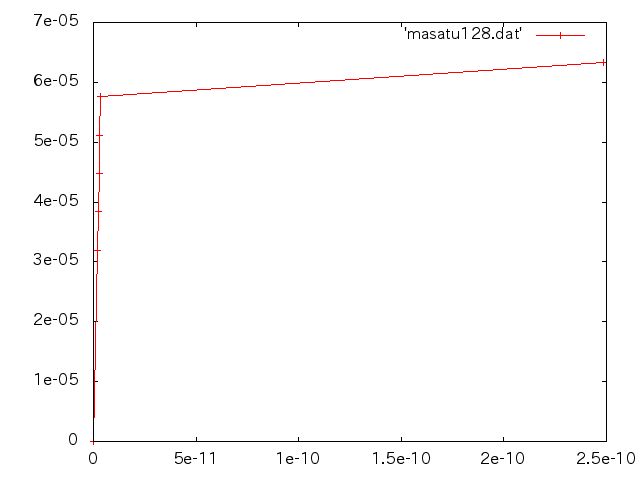

| 応力(MPa) | 伸び(m) | ひずみ | ヤング率(GPa) |
| 50 | 2.420E-4 | 2.420E-4 | 206.6 |
| 100 | 4.839E-4 | 4.839E-4 | 206.7 |
| 150 | 7.259E-4 | 7.259E-4 | 206.6 |
| 200 | 9.681E-4 | 9.681E-4 | 206.6 |
| 230 | 1.114E-3 | 1.114E-3 | 206.5 |
| 235 | 3.234E-3 | 3.234E-3 |
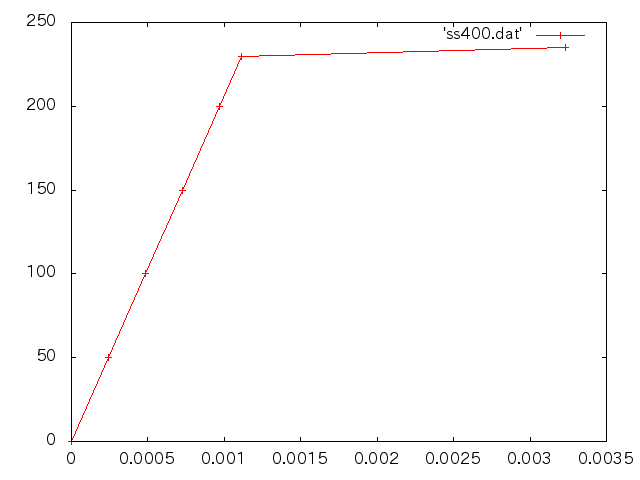
| 応力(MPa) | 伸び(m) | ひずみ | ヤング率(GPa) |
| 100 | 4.846E-4 | 4.839E-4 | 206.4 |
| 200 | 9.671E-4 | 9.671E-4 | 206.8 |
| 235 | 1.151E-3 | 1.151E-3 | 204.2 |
| 250 | 9.251E-1 | 9.251E-1 | |
| 300 | 4.502E-0 | 4.502E-0 | |
| 400 | 11.66 | 11.66 |
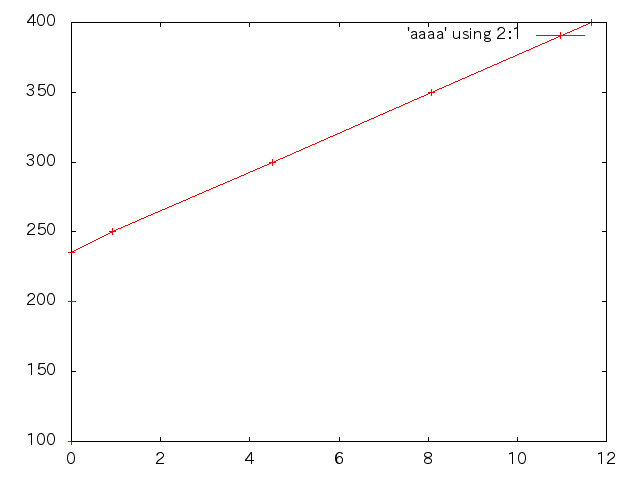
| 応力(MPa) | 塑性ひずみ |
| 235 | 0 |
| 235.1 | 5.05705E-2 |
| 235.2 | 1.005705E-1 |
| 235.3 | 1.505705E-1 |
| 235.4 | 2.005705E-1 |
| 235.5 | 2.505705E-1 |
| 応力(MPa) | 変位(m) | ひずみ |
| 100 | 4.836E-4 | 4.836E-4 |
| 200 | 9.671E-4 | 9.671E-4 |
| 235 | 2.083E-3 | 2.083E-3 |
| 235.1 | 6.229E-3 | 6.229E-3 |
| 235.2 | 1.258E-2 | 1.258E-2 |
| 235.3 | 1.856E-2 | 1.856E-2 |
| 235.4 | 2.433E-2 | 2.433E-2 |
| 235.5 | 3.015E-2 | 3.015E-2 |
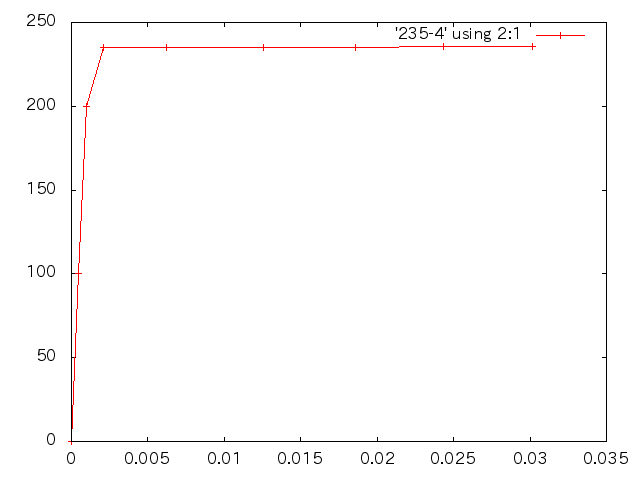
| 応力(MPa) | 塑性ひずみ |
| 235 | 0 |
| 235.1 | 5.05705E-3 |
| 235.2 | 1.005705E-2 |
| 235.3 | 1.505705E-2 |
| 235.4 | 2.005705E-2 |
| 235.5 | 2.505705E-2 |
| 応力(MPa) | 変位(m) | ひずみ |
| 100 | 4.836E-4 | 4.836E-4 |
| 200 | 9.671E-4 | 9.671E-4 |
| 235 | 1.316E-3 | 1.775E-3 |
| 235.1 | 3.829E-3 | 3.829E-3 |
| 235.2 | 6.453E-3 | 6.453E-3 |
| 235.3 | 8.930E-3 | 8.930E-3 |
| 235.4 | 1.143E-2 | 1.143E-2 |
| 235.5 | 1.394E-2 | 1.394E-2 |
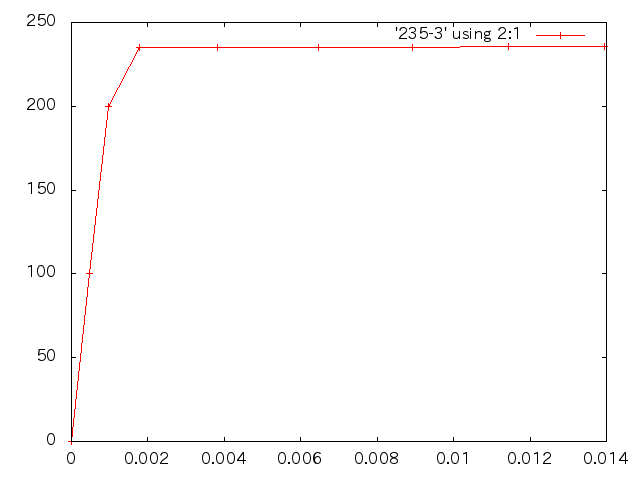
| 応力(MPa) | 塑性ひずみ |
| 235 | 0 |
| 235.1 | 5.05705E-4 |
| 235.2 | 1.005705E-3 |
| 235.3 | 1.505705E-3 |
| 235.4 | 2.005705E-3 |
| 235.5 | 2.505705E-3 |
| 応力(MPa) | 変位(m) | ひずみ |
| 100 | 4.836E-4 | 4.836E-4 |
| 200 | 9.671E-4 | 9.671E-4 |
| 235 | 1.316E-3 | 1.316E-3 |
| 235.1 | 1.738E-3 | 1.738E-3 |
| 235.2 | 2.119E-3 | 2.119E-3 |
| 235.3 | 2.508E-3 | 2.508E-3 |
| 235.4 | 2.902E-3 | 2.902E-3 |
| 235.5 | 3.298E-3 | 3.298E-3 |
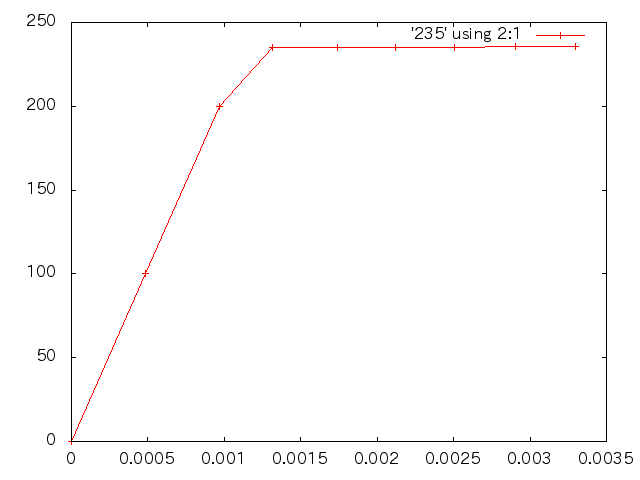
| 応力(MPa) | 塑性ひずみ |
| 235 | 0 |
| 235.1 | 5.05705E-5 |
| 235.2 | 1.005705E-4 |
| 235.3 | 1.505705E-4 |
| 235.4 | 2.005705E-4 |
| 235.5 | 2.505705E-4 |
| 応力(MPa) | 変位(m) | ひずみ |
| 100 | 4.836E-4 | 4.836E-4 |
| 200 | 9.671E-4 | 9.871E-4 |
| 235 | 1.183E-3 | 1.183E-3 |
| 235.1 | 1.225E-3 | 1.225E-3 |
| 235.2 | 1.270E-3 | 1.270E-3 |
| 235.3 | 1.315E-3 | 1.315E-3 |
| 235.4 | 1.361E-3 | 1.361E-3 |
| 235.5 | 1.406E-3 | 1.406E-3 |
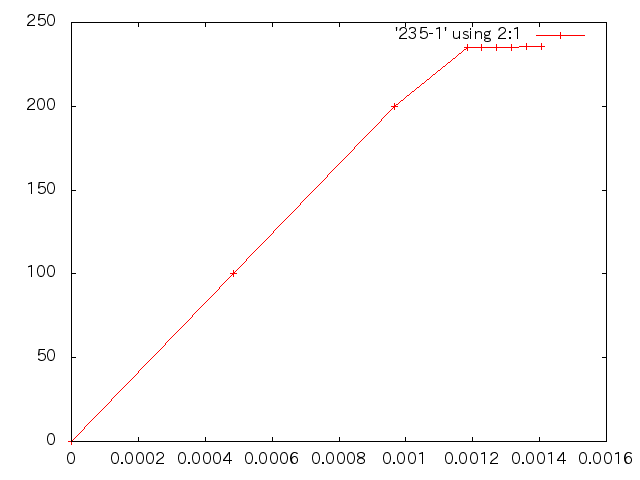
| 応力(MPa) | 塑性ひずみ |
| 235 | 0 |
| 235.1 | 5.05705E-6 |
| 235.2 | 1.005705E-5 |
| 235.3 | 1.505705E-5 |
| 235.4 | 2.005705E-5 |
| 235.5 | 2.505705E-5 |
| 応力(MPa) | 変位(m) | ひずみ |
| 100 | 4.836E-4 | 4.836E-4 |
| 200 | 9.671E-4 | 9.671E-4 |
| 235 | 1.151E-3 | 1.151E-3 |
| 235.1 | 1.150E-3 | 1.150E-3 |
| 235.2 | 1.155E-3 | 1.155E-3 |
| 235.3 | 1.160E-3 | 1.160E-3 |
| 235.4 | 1.170E-3 | 1.170E-3 |
| 235.5 | 1.170E-3 | 1.170E-3 |
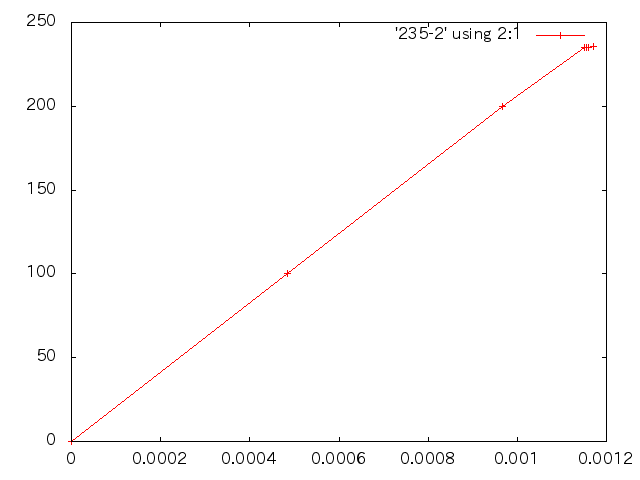
FACELOAD を400付近で変えてみる 長さ1mなので伸び=ひずみ
断面分割数nx=ny=12,軸方向分割数=100
| FACELOAD | 最大変位(m) | 逆算ヤング率(GPa) |
| 380 | 1.840e-3 | |
| 390 | 1.893e-3 | |
| 399 | 2.050e-3 | |
| 399.9 | 2.329e-3 | |
| 400 | 5.732e-3 | |
| 401 | 不明 15分以上掛かりそう |
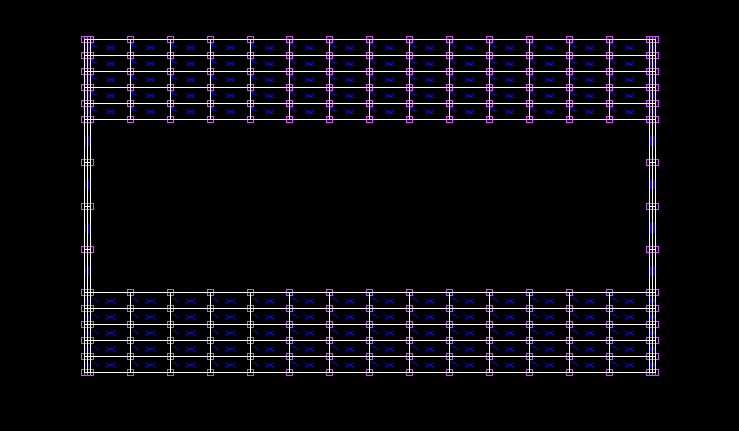
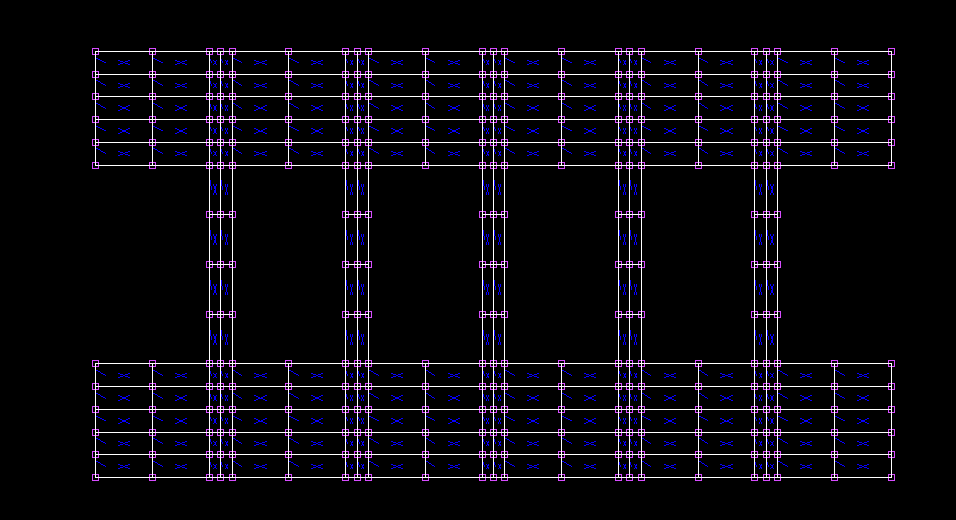

| x(m) | 変位(m) |
| 0 | 5.46194E-03 |
| 0.06 | 5.40277E-03 |
| 0.12 | 5.37674-03 |
| 0.132 | 5.37784E-03 |
| 0.144 | 5.36153E-03 |
| 0.204 | 5.31605E-03 |
| 0.264 | 5.30943E-03 |
| 0.276 | 5.31517E-03 |
| 0.288 | 5.30314E-03 |
| 0.348 | 5.27756E-02 |
| 0.408 | 5.28814E-03 |
| 0.420 | 5.29707E-03 |
| 0.432 | 5.28814E-03 |
| 0.492 | 5.27756E-03 |
| 0.552 | 5.30314E-03 |
| 0.564 | 5.31517E-03 |
| 0.576 | 5.30943E-03 |
| 0.636 | 5.31605E-03 |
| 0.696 | 5.36153E-03 |
| 0.708 | 5.37784E-03 |
| 0.720 | 5.37674E-03 |
| 0.780 | 5.40227E-03 |
| 0.840 | 5.46194E-03 |
| x(m) | 変位(m) |
| 0 | 5.57192E-03 |
| 0.060 | 5.46803E-03 |
| 0.120 | 5.40478E-03 |
| 0.132 | 5.39994E-03 |
| 0.144 | 5.37865E-03 |
| 0.204 | 5.31558E-03 |
| 0.264 | 5.29956E-03 |
| 0.276 | 5.30416E-03 |
| 0.288 | 5.2914E-03 |
| 0.348 | 5.26369E-03 |
| 0.408 | 5.27337E-03 |
| 0.420 | 5.2822E-03 |
| 0.432 | 5.27337E-03 |
| 0.492 | 5.26369E-03 |
| 0.552 | 5.2914E-03 |
| 0.564 | 5.30416E-03 |
| 0.576 | 5.29956E-03 |
| 0.636 | 5.31558E-02 |
| 0.696 | 5.37865E-03 |
| 0.708 | 5.39994E-03 |
| 0.720 | 5.40478E-03 |
| 0.780 | 5.46803E-03 |
| 0.840 | 5.57192E-03 |
| 分割数(nz) | たわみ(m) | 相対誤差(%) |
| 2 | 3.693E-03 | 39.32 |
| 4 | 4.964E-02 | 18.44 |
| 8 | 5.511E-02 | 9.45 |
| 16 | 5.719E-02 | 6.03 |
| 32 | 5.816E-02 | 4.44 |
| 64 | 5.882E-02 | 3.35 |
| 128 | 5.930E-02 | 2.56 |
| 256 | 5.956E-02 | 2.14 |
| 512 | 5.965E-02 | 1.99 |
| 理論値 | 6.086E-03 |
| ccx | mentat | ||
| 幅方向x(m) | 変位(m) | 幅方向x(m) | 変位(m) |
| 0 | 1.363617E-02 | 0 | 1.36548E-02 |
| 0.06 | 1.35057E-02 | 0.06 | 1.35057E-02 |
| 0.12 | 1.34418E-02 | 0.12 | 1.34418E-02 |
| 0.132 | 1.34446E-02 | 0.132 | 1.34446E-02 |
| 0.144 | 1.34038E-02 | 0.144 | 1.34038E-02 |
| 0.204 | 1.32901E-02 | 0.204 | 1.32901E-02 |
| 0.264 | 1.32736E-02 | 0.264 | 1.32736E-02 |
| 0.276 | 1.32879E-02 | 0.276 | 1.32879E-02 |
| 0.288 | 1.32578E-02 | 0.288 | 1.32578E-02 |
| 0.348 | 1.31939E-02 | 0.348 | 1.31939E-02 |
| 0.408 | 1.32203E-02 | 0.408 | 1.32203E-02 |
| 0.420 | 1.32427E-02 | 0.420 | 1.32427E-02 |
| 0.432 | 1.32203E-02 | 0.432 | 1.32203E-02 |
| 0.492 | 1.31939E-02 | 0.492 | 1.31939E-02 |
| 0.552 | 1.32578E-02 | 0.552 | 1.32578E-02 |
| 0.564 | 1.32879E-02 | 0.564 | 1.32879E-02 |
| 0.576 | 1.32736E-02 | 0.576 | 1.32736E-02 |
| 0.636 | 1.32901E-02 | 0.636 | 1.32901E-02 |
| 0.696 | 1.34038E-02 | 0.696 | 1.34038E-02 |
| 0.708 | 1.34446E-02 | 0.708 | 1.34446E-02 |
| 0.720 | 1.34418E-02 | 0.720 | 1.34418E-02 |
| 0.780 | 1.35057E-02 | 0.780 | 1.35057E-02 |
| 0.840 | 1.36548E-02 | 0.840 | 1.36548E-02 |
| 分割数 | calculix | 分割数 | mentat | ||
| nz | たわみ(m) | 相対誤差(%) | nz | たわみ(m) | 相対誤差(%) |
| 2 | 8.811E-03 | 42.09 | 2 | 8.786E-03 | 42.25 |
| 4 | 1.186E-02 | 22.05 | 4 | 1.183E-02 | 22.25 |
| 8 | 1.307E-02 | 14.10 | 8 | 1.306E-02 | 14.16 |
| 16 | 1.346E-02 | 11.53 | 16 | 1.347E-02 | 11.47 |
| 32 | 1.358E-02 | 10.75 | 32 | 1.360E-02 | 10.61 |
| 64 | 1.362E-02 | 10.48 | 64 | 1.365E-02 | 10.29 |
| 128 | 1.363E-02 | 10.42 | 128 | 1.367E-02 | 10.15 |
| 256 | 1.364E-02 | 10.35 | 256 | 1.367E-02 | 10.15 |
| 512 | 1.365E-02 | 10.29 | 512 | 1.367E-02 | 10.15 |
| 理論値 | 1.5215E-02 |
六面体要素の: face 1: 1-2-3-4 face 2: 5-8-7-6 face 3: 1-5-6-2 face 4: 2-6-7-3 face 5: 3-7-8-4 face 6: 4-8-5-1 四面体要素の: Face 1: 1-2-3 Face 2: 1-4-2 Face 3: 2-4-3 Face 4: 3-4-1 くさび形要素の: Face 1: 1-2-3 Face 2: 4-5-6 Face 3: 1-2-5-4 Face 4: 2-3-6-5 Face 5: 3-1-4-6 四辺形平面応力、平面ひずみと軸対称要素の場合: Face 1: 1-2 Face 2: 2-3 Face 3: 3-4 Face 4: 4-1 三角形平面応力、平面ひずみと軸対称要素の場合: Face 1: 1-2 Face 2: 2-3 Face 3: 3-1 梁要素の場合: Face 1: pressure in 1-direction Face 2: pressure in 2-directionただひとつの種類の荷重(シェル上の法線方向の圧力)があるので、シェル要素には面番号は必要ありません。
| h2(m) | 相対誤差(%) |
| 2.80000E-01 | -2.91321E+01 |
| 3.20000E-01 | -2.70221E+01 |
| 3.60000E-01 | -2.53371E+01 |
| 4.00000E-01 | -2.38924E+01 |
| 4.40000E-01 | -2.26134E+01 |
| 4.80000E-01 | -2.14579E+01 |
| 5.20000E-01 | -2.03999E+01 |
| 5.60000E-01 | -1.94169E+01 |
| 6.00000E-01 | -1.84997E+01 |
| 6.40000E-01 | -1.76312E+01 |
| 6.80000E-01 | -1.68089E+01 |
| 7.20000E-01 | -1.60234E+01 |
| 7.60000E-01 | -1.52692E+01 |
| 8.00000E-01 | -1.45412E+01 |
| 8.40000E-01 | -1.38387E+01 |
| 8.80000E-01 | -1.31560E+01 |
| 9.20000E-01 | -1.24906E+01 |
| 9.60000E-01 | -1.18417E+01 |
| 1.00000E+00 | -1.12070E+01 |
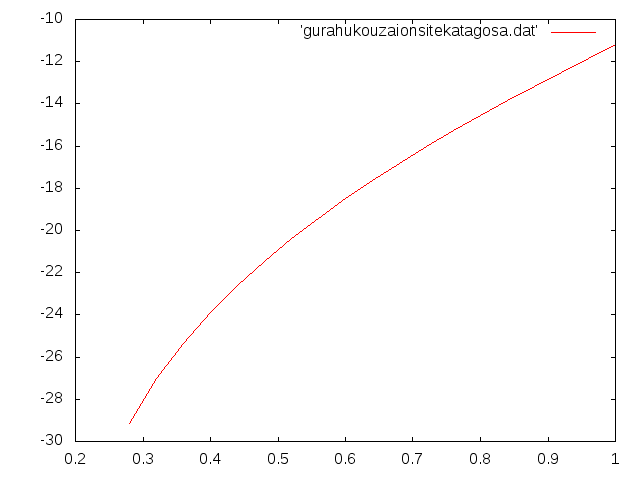
| h2(m) | 相対誤差(%) |
| 6.80000E-02 | -9.16908E+01 |
| 1.18000E-01 | -8.69721E+01 |
| 1.68000E-01 | -8.20985E+01 |
| 2.18000E-01 | -7.72230E+01 |
| 2.68000E-01 | -7.24022E+01 |
| 3.18000E-01 | -6.76740E+01 |
| 3.68000E-01 | -6.30595E+01 |
| 4.18000E-01 | -5.85704E+01 |
| 4.68000E-01 | -5.42178E+01 |
| 5.18000E-01 | -5.00031E+01 |
| 5.68000E-01 | -4.59331E+01 |
| 6.18000E-01 | -4.20035E+01 |
| 6.68000E-01 | -3.82223E+01 |
| 7.18000E-01 | -3.45813E+01 |
| 7.68000E-01 | -3.10793E+01 |
| 8.18000E-01 | -2.77155E+01 |
| 8.68000E-01 | -2.44874E+01 |
| 9.18000E-01 | -2.13888E+01 |
| 9.68000E-01 | -1.84182E+01 |
| 1.01800E+00 | -1.55690E+01 |
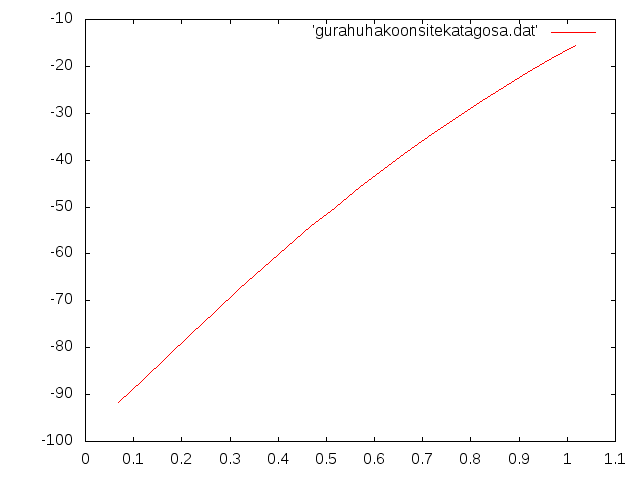
| h2(m) | 相対誤差(%) |
| 6.80000E-02 | -5.45343E+00 |
| 1.18000E-01 | -3.88840E+00 |
| 1.68000E-01 | -3.48379E+00 |
| 2.18000E-01 | -3.25848E+00 |
| 2.68000E-01 | -3.06076E+00 |
| 3.18000E-01 | -2.86775E+00 |
| 3.68000E-01 | -2.66288E+00 |
| 4.18000E-01 | -2.44449E+00 |
| 4.68000E-01 | -2.20650E+00 |
| 5.18000E-01 | -1.95315E+00 |
| 5.68000E-01 | -1.67852E+00 |
| 6.18000E-01 | -1.38560E+00 |
| 6.68000E-01 | -1.06950E+00 |
| 7.18000E-01 | -7.40961E-01 |
| 7.68000E-01 | -3.85094E-01 |
| 8.18000E-01 | -1.02293E-02 |
| 8.68000E-01 | 3.84346E-01 |
| 9.18000E-01 | 7.99488E-01 |
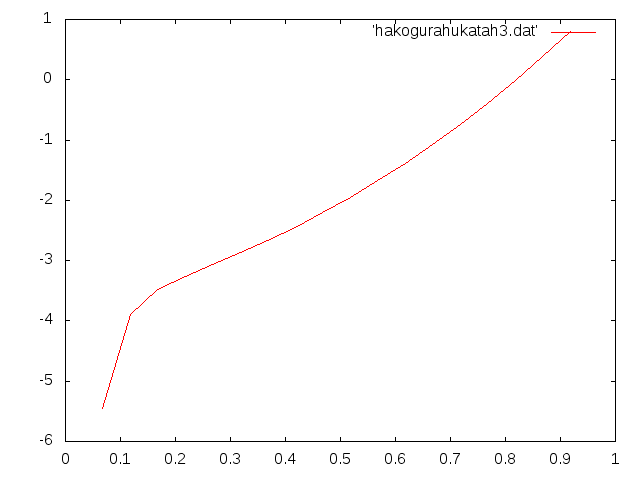
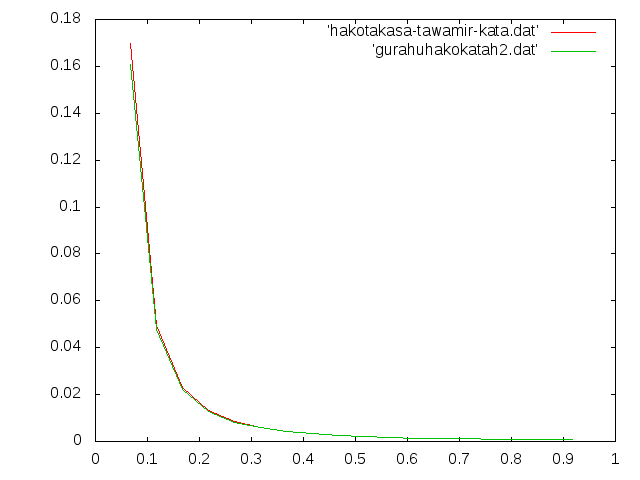

| h2(m) | 相対誤差(%) |
| 6.80000E-02 | -5.45343E+00 |
| 1.18000E-01 | -3.88840E+00 |
| 1.68000E-01 | -3.48379E+00 |
| 2.18000E-01 | -3.25848E+00 |
| 2.68000E-01 | -3.06076E+00 |
| 3.18000E-01 | -2.86775E+00 |
| 3.68000E-01 | -2.66288E+00 |
| 4.18000E-01 | -2.44449E+00 |
| 4.68000E-01 | -2.20650E+00 |
| 5.18000E-01 | -1.95315E+00 |
| 5.68000E-01 | -1.67852E+00 |
| 6.18000E-01 | -1.38560E+00 |
| 6.68000E-01 | -1.06950E+00 |
| 7.18000E-01 | -7.40961E-01 |
| 7.68000E-01 | -3.85094E-01 |
| 8.18000E-01 | -1.02293E-02 |
| 8.68000E-01 | 3.84346E-01 |
| 9.18000E-01 | 7.99488E-01 |
| h2(m) | たわみ(m) |
| 0.3 | 1.2162E-02 |
| 0.4 | 6.7682E-03 |
| 0.5 | 4.5888E-03 |
| 0.6 | 3.4692E-03 |
| 0.7 | 2.8055E-03 |
| 0.8 | 2.3735E-03 |
| 0.9 | 2.0733E-03 |
| h2(m) | たわみ(m) |
| 0.3 | 2.4269E-02 |
| 0.4 | 1.0855E-02 |
| 0.5 | 5.9180E-03 |
| 0.6 | 3.6444E-03 |
| 0.7 | 2.4355E-03 |
| 0.8 | 1.7259E-03 |
| 0.9 | 1.2785E-03 |
| nz | たわみ(m) | 相対誤差(%) |
| 2 | 3.5446E-03 | -41.992 |
| 4 | 4.7644E-03 | -22.029 |
| 8 | 5.2480E-03 | -14.115 |
| 16 | 5.4036E-03 | -11.569 |
| 32 | 5.4524E-03 | -10.770 |
| 64 | 5.4686E-03 | -10.505 |
| 128 | 5.4742E-03 | -10.413 |
| 256 | 5.4758E-03 | -10.387 |
| 512 | 5.4736E-03 | -10.379 |
| 理論値 | 6.1105E-03 |
| nz | たわみ(m) | 相対誤差(%) |
| 2 | 1.9384E-03 | -70.196 |
| 4 | 3.8697E-03 | -40.502 |
| 8 | 5.1826E-03 | -20.316 |
| 16 | 5.6916E-03 | -12.489 |
| 32 | 5.8493E-03 | -10.065 |
| 64 | 5.8966E-03 | -9.3375 |
| 128 | 5.9114E-03 | -9.1099 |
| 256 | 5.9163E-03 | -9.0346 |
| 512 | 5.9180E-03 | -9.0084 |
| 理論値 | 6.5039E-03 |
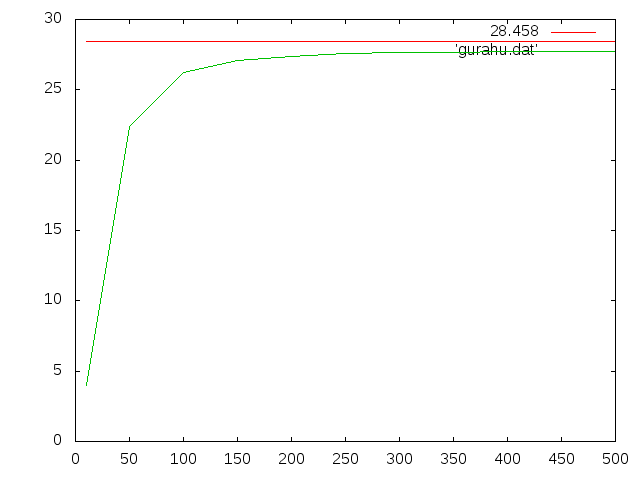
| length | 要素数 | たわみ(m) | 相対誤差(%) |
| 20000 | 398 | 1.5654E-03 | -96.488 |
| 15000 | 514 | 3.5413E-03 | -87.531 |
| 10000 | 1256 | 6.5277E-03 | -77.015 |
| 5000 | 5304 | 1.0370E-02 | -63.486 |
| 2500 | 21767 | 1.7528E-02 | -38.282 |
| 1200 | 173811 | 2.5647E-02 | -9.6937 |
| 1000 | 176011 | 2.5657E-02 | -9.6585 |
| 800 | 184862 | 2.5674E-02 | -9.5986 |
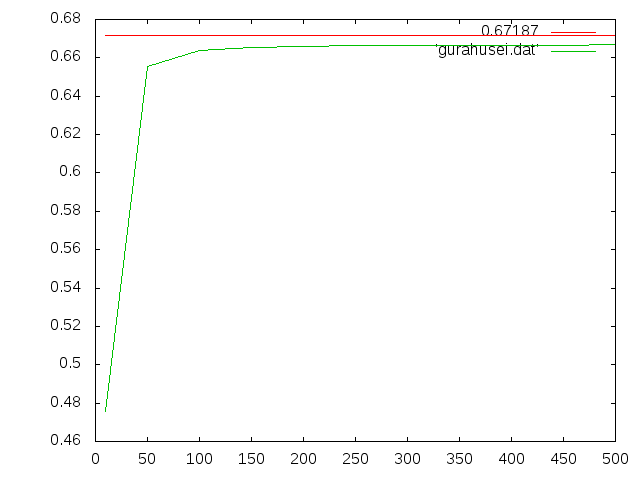
| length | 要素数 | たわみ(m) | 相対誤差(%) |
| 20000 | 373 | 3.5819E-04 | -46.688 |
| 15000 | 584 | 4.0795E-04 | -39.281 |
| 10000 | 1761 | 5.1320E-04 | -23.616 |
| 5000 | 8128 | 5.9328E-04 | -11.697 |
| 2500 | 41234 | 6.2908E-04 | -6.3688 |
| 1200 | 190758 | 6.5535E-04 | -2.4588 |
| 1000 | 343661 | 6.6252E-04 | -1.3916 |
| 800 | 389934 | 6.6245E-04 | -1.4021 |
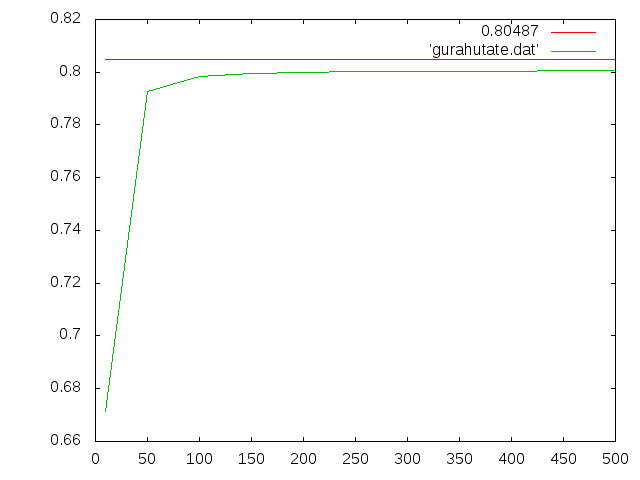
| length | 要素数 | たわみ(m) | 相対誤差(%) |
| 20000 | 380 | 5.1029E-04 | -36.600 |
| 15000 | 482 | 5.8365E-04 | -27.485 |
| 10000 | 1226 | 7.2589E-04 | -9.8128 |
| 5000 | 5229 | 7.7913E-04 | -3.1980 |
| 2500 | 21510 | 7.9245E-04 | -1.5431 |
| 1200 | 149064 | 7.9837E-04 | -0.8758 |
| 1000 | 150875 | 7.9834E-04 | -0.81131 |
| 800 | 157030 | 7.9845E-04 | 0.79764 |